скорость движения электрона.
Марина Заблоцкая
Ученик
(88),
закрыт
10 лет назад
Определить скорость движения электрона. длина волны де Бройля которого составляет 1.5*10^-10м.
Валентина Вавилова(Серкова)
Гений
(62183)
10 лет назад
По формуле длины волны де Бройля
лямбда=h / m*v. ( лямбда – длина волны, h -постоянная Планка, m -масса электрона=9.1*10^(-31)кг, v -скорость ) выразим скорость
v=h / m*лямбда.
v=6,63*10^(-34) / 9,1*10^(-31)*1,5*10^(-10)=4,86*10^6м/c.
Условие задачи:
С какой скоростью должен двигаться электрон, чтобы его импульс был равен импульсу фотона с длиной волны, равной 520 нм?
Задача №11.1.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(lambda=520) нм, (upsilon-?)
Решение задачи:
Импульс электрона (p), движущегося со скоростью (upsilon), можно определить по следующей формуле:
[p = {m_e}upsilon;;;;(1)]
Здесь ({m_e}) – масса электрона, равная 9,1·10-31 кг.
Также запишем формулу длины волны де Бройля (lambda):
[lambda = frac{h}{p}]
В этой формуле (h) – это постоянная Планка, равная 6,62·10-34 Дж·с.
Откуда выразим импульс фотона (p):
[p = frac{h}{lambda };;;;(2)]
Приравняем правые части формул (1) и (2):
[{m_e}upsilon = frac{h}{lambda }]
Откуда искомая скорость электрона (upsilon) равна:
[upsilon = frac{h}{{{m_e}lambda }}]
Посчитаем теперь численный ответ задачи:
[upsilon = frac{{6,62 cdot {{10}^{ – 34}}}}{{9,1 cdot {{10}^{ – 31}} cdot 520 cdot {{10}^{ – 9}}}} = 1400;м/с]
Ответ: 1400 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
11.1.15 Определить импульс фотона, соответствующего рентгеновскому излучению с частотой
11.1.17 При какой длине волны излучения масса фотона равна массе покоя электрона?
11.1.18 Источник мощностью в 100 Вт испускает 5*10^20 фотонов за 1 с. Найти среднюю
В этой статье мы собираемся обдумать взаимосвязь энергии и длины волны вместе с примерами и решить некоторые задачи, чтобы проиллюстрировать то же самое.
Энергия находится в прямой зависимости от частоты электромагнитных излучений. Если длина волны увеличивается, это означает, что повторяемость волны будет уменьшаться, что непосредственно влияет на энергию частицы в волне.
Формула соотношения энергии и длины волны
Энергия частицы может быть связана с ее скоростью во время распространения. Скорость частицы дает представление о частоте и длине волны. Если длина волны мала, то частота и, следовательно, энергия частицы будут увеличиваться.
Если колебания частицы больше в траектории пути, то возвратность частицы в волну больше и длина волны мала, это означает, что энергия, которой обладает частица, больше.
Энергия любого тела связана с его длиной волны уравнением
E=hc/λ
Где «h» — постоянная Планка h = 6.626 * 10-34Js
C – скорость света c=3 *108 м/с и
λ – длина волны света
Энергия обратно пропорциональна длине волны света. Чем меньше длина волны, тем больше энергия частицы в волне.
Задача 1: Рассчитать энергию фотонов, испускающих красный свет. Считайте длину волны луча красного света равной 698 нм. Какова будет энергия, если длина волны уменьшится до 500 нм, то есть если источник излучает зеленый свет?
Данный:λ1=698нм
λ2=500 нм
ч = 6.626 * 10-34 Js
с=3 * 108 м/с
У нас есть,
E=hc/λ1
E = 6.626 * 10-34 Дж* 3 * 108 м/с/698* 10-9m
=0.028* 10-17=28* 10-20Дж
Энергия красной длины волны 28* 10-20Джоули.
Если длина волны λ2=500 нм
Тогда энергия, связанная с зеленым светом, равна
E=hc/λ2
E = 6.626 * 10-34 Дж* 3 * 108 м/с / 500* 10-9m
= 0.03910-17=39* 10-20Дж
Мы видим, что энергия увеличилась до 39*10-20 Джоулей при уменьшении длины волны.
Подробнее о Влияние преломления на длину волны: как, почему, подробные факты.
График взаимосвязи энергии и длины волны
По мере увеличения длины волны частота волны падает, тем самым уменьшая энергию, которой обладает волна. Если мы построим график зависимости энергии от длины волны появляющейся частицы, то график будет выглядеть так, как показано ниже.
Приведенный выше график ясно показывает, что по мере увеличения длины волны энергия, связанная с частицей, уменьшается экспоненциально.
Связь кинетической энергии и длины волны
Если скорость частицы больше, то очевидно, что кинетическая энергия частицы велика. Кинетическая энергия определяется уравнением
КЭ=1/2мВ2
Где m – масса объекта или частицы
V – скорость массы
Мы можем записать приведенное выше уравнение как
2E=мв2
Умножение «m» в обеих частях уравнения
2mE=(мВ)2
Импульс объекта определяется как произведение массы объекта на скорость, с которой он движется.
p = mv
Следовательно, приведенное выше уравнение становится
P2=2 мВ
P=√2mE
Согласно де Бройлю,
λ =h/p
Подставляя приведенное выше уравнение, мы имеем
λ =h/ √2mE
Приведенное выше уравнение дает связь между энергией и длиной волны частицы.
Подробнее о Что такое кинетическая энергия света: подробные факты.
Задача 2. Вычислить кинетическую энергию частицы массой 9.1 × 10-31 кг с длиной волны 293 нм. Кроме того, найдите скорость частицы.
Данный: λ = 293 нм
м = 9.1 × 10-31 kg
ч = 6.626 * 10-34Js
с=3 *108 м/с
У нас есть,
λ =h/ √2mE
λ2=h2/ 2мЕ
Е = ч2/ 2мλ2
=(6.626 * 10-34 Дж)2/2* 9.1* 10-31* (293*10-9) 2
= 0.28 * 10-23
Кинетическая энергия, связанная с частицей, равна 0.28*10-23 Джоули.
Теперь, чтобы вычислить скорость частицы, выведем формулу скорости из кинетической энергии:
КЕ=1/2 мВ2
2E= мв2
v=√(2Е/м)
= √(2(0.28*10-23)/(9.8*10-31))
= 0.24 * 104= 2400 м / с
Скорость частицы с длиной волны 298 нм составляет 2400 м/с.
Связь энергии электрона и длины волны
Энергия электрона определяется простым уравнением:
Е=чню
Где «h» — постоянная Планка, а
nu – частота появления электрона
Частота электрона определяется как
ню = v / λ
Где v – скорость электрона и
λ – длина волны электронной волны
Следовательно, энергия связана с длиной волны электрона как
E=hv/λ
Это соотношение позволяет найти энергию, связанную с распространением одиночного электрона с определенной длиной волны, скоростью и частотой. Энергия обратно пропорциональна длине волны. Если длина волны электрона уменьшается, энергия волны должна быть больше.
Изображение Фото: Pixabay
Получив энергию в той или иной форме, электрон переходит из более низкого энергетического состояния в более высокое энергетическое состояние. Для перехода электронов из одного состояния в другое энергия электрона определяется уравнением
Э=РE(1/нf– 1/нi)
Где RE=-2.18* 10-18m-1 является константой Ридберга
nf это конечное состояние электрона
ni это начальное состояние электрона
Мы можем далее переписать приведенное выше уравнение как
ч ню = RE(1/нf– 1/нi)
hc/λ =RE(1/нf– 1/нi)
1/λ =REhc(1/nf– 1/нi)
1/λ =R(1/nf– 1/нi)
Где,
Р=РEчс=1.097* 107
По мере того, как электрон получает энергию, электрон переходит и перескакивает в более высокое состояние энергетического уровня и высвобождает энергию электронам, присутствующим в этом состоянии, и либо становится стабильным, либо высвобождает количество энергии и возвращается в более низкие энергетические состояния.
Подробнее о 16+ Пример амплитуды волны: подробные пояснения.
Задача 3: Если электрон переходит из состояния ni=1, чтобы указать nf=2, затем рассчитайте длину волны электрона.
Данный:
ni=1
nf=2
1/λ =RE(1/нf– 1/нi)
1/λ=-1.097*107 * ( 1/2-1/1 )
1/λ=0.5485* 107
Следовательно,
λ = 1/0.5485* 107
λ =1.823*10-7
λ =182.3*10-9=182.3нм
Длина волны света, излучаемого при переходе электрона с одного энергетического уровня на другой, равна 182.3 нм.
Связь лучистой энергии и длины волны
Каждый объект поглощает световые лучи в дневное время в зависимости от его формы, размера и состава. Если температура поверхности объекта достигает температуры выше абсолютного нуля, объект будет излучать излучения в виде волн.
Это испускаемое излучение пропорционально четвертой степени абсолютной температуры объекта и определяется уравнением
U=ɛΣ Т4A
Где U – излучаемая энергия
ɛ – коэффициент излучения излучения от объекта
Σ — постоянная Стефана-Больцмана, равная Σ=5.67*10-8Вт / м2K4
T – абсолютная температура
А – площадь объекта
Объект с высокой температурой излучает излучение с короткими длинами волн, а более холодные поверхности излучают волны с большей длиной волны. В зависимости от испускаемого излучения и длины волны испускаемого излучения волны классифицируются в соответствии с приведенной ниже таблицей.
| Имя и фамилия | Радиоволны | Микроволны | Инфракрасный порт | Видимый | Ультрафиолетовое | рентген | Гамма излучение |
| Длина волны | > 1м | 1mm-1m | 700нм-1мм | 400nm-700nm | 10nm-380nm | 0.01nm-10nm | <0.01 нм |
| частота | <300 МГц | 300MHz-300GHz | 300ГГц-430ТГц | 430ТГц-750ТГц | 750ТГц-30ФГц | 30PHz-30EHz | >30 Гц |
По мере уменьшения длины волны излучения частота волны возрастает. Длина волны напрямую связана с температурой, поэтому, если частота испускаемого излучения больше, это означает, что энергия объекта высока.
Гамма-лучи, рентгеновские лучи и ультрафиолетовые лучи имеют очень короткую длину волны, поэтому энергия этих волн очень высока по сравнению с видимым, инфракрасным, микроволнами или радиоволнами. Кроме того, чем выше излучение, полученное объектом, тем больше он будет излучать в зависимости от коэффициента излучения объекта.
Ниже приведен график зависимости энергии от длины волны в секунду для разных температур. График показывает, что по мере повышения температуры системы энергия испускаемого излучения также увеличивается с температурой.
Для длины волны в видимой области эмиссия излучения максимальна. Это связано с тем, что Солнце излучает УФ-лучи вместе с инфракрасными лучами и видимыми лучами, а эти лучи представляют собой электромагнитные волны дальнего действия. Озоновый слой Земли защищает земную атмосферу от этого вредного излучения и либо отражается обратно, либо задерживается в облаках.
В видимом диапазоне в дневное время излучается больше излучений, поскольку в дневное время от Солнца поступает все больше и больше излучений, а испускается меньше ИК-лучей по сравнению с видимым спектром. Ночью температура снижается, длина волны излучения увеличивается, и объект излучает больше ИК-лучей.
Подробнее о Свойства преломления: волна, физические свойства, исчерпывающие факты.
Задача 4: Коробка длиной 11 см, шириной 2 см и воздухом 7 см нагревается до температуры 1200 Кельвинов. Если коэффициент излучения ящика равен 0.5, то рассчитайте скорость излучения энергии из ящика.
Данный:л=11см
ч=2см
б = 7cm
е =0.5
Σ=5.67* 10-8Вт / м2K4
Т=1200 К
Общая площадь ящика составляет
A=2(фунт+чб+гл)
=2(11*7+7*s 2+2*11)
=2 (77+14+22)
=0.0226 кв.м
Энергия, излучаемая коробкой, равна
U=ɛ Σ T4A
=0.5* 5.67* 10-8* 12004* 0.0226
=1328.6 Вт
Связь частоты энергии и длины волны
Чем больше частота волны, тем больше энергия, связанная с частицей. Энергия связана с частотой волны как
E=ч/ню
Где «h» — постоянная Планка.
nu – частота волны
Частота волны определяется как скорость волны в среде и длина волны.
ню = v / λ
Где v – скорость волны
λ – длина волны
Следовательно,
λ=v/ну
Это дает связь между частотой и длиной волны волны. Это говорит о том, что длина волны и частота обратно пропорциональны друг другу. Если длина волны увеличивается, частота волны уменьшится.
Подробнее о Влияние преломления на частоту: как, почему нет, подробные факты.
Задача 5. Скорость луча света, испускаемого источником, равна 1.9 × 108 РС. Частота возникновения излучаемой волны составляет 450ТГц. Найдите длину волны испускаемого излучения.
Данный: v=1.9*108 м/с
F=450ТГц=450*1012Hz
Длина волны луча света равна
λ = v/f
=1.9* 108/ 450* 1012
= 0.004222 * 10-4
=422.2* 10-9=422.2нм
Луч света имеет длину волны 422.2 нм.
Связь энергии фотона и длины волны
Энергия, которой обладает фотон, называется энергией фотона и обратно пропорциональна электромагнитной волне фотона по соотношению
E=hc/λ
Где «h» — постоянная Планка.
С – скорость света
λ – длина волны фотона
Частота фотона определяется уравнением
f=с/λ
Где f – частота
Следовательно, фотон с большей длиной волны обладает небольшой единицей энергии, тогда как фотон с меньшей длиной волны дает большое количество энергии.
Подробнее о Какова длина волны фотона: как найти, несколько идей и фактов.
Задача 6: Рассчитать энергию фотона, распространяющегося в электромагнитной волне с длиной волны 620 нм.
Данный: Длина волныλ =620 нм
ч = 6.626 * 10-34 js
с=3 *108 м/с
У нас есть,
E=hc/λ
Е=6.626 * 10-34 Дж*3 * 108 м/с/620* 10-9m
= 0.032 * 10-17= 32 * 10-20 Дж
Энергия, связанная с фотоном, равна 32* 10-20Джоули.
Часто задаваемые вопросы
Q1. Вычислите длину волны электрона, движущегося со скоростью 6.35 × 106 м/с
Данный: v=6.35*106м/с
м=9.1*10-31kg
ч=6.62* 10-34 Js
Кинетическая энергия электрона равна
КЕ=1/2 мВ2
=1/2 * 9.1*10-31* (6.35* 106)2
=1.83* 10-17Дж
Импульс электрона равен
P=√2mE
=√2* 9.1* 10-31* 1.83 * 10-17
= 5.7 * 10-24кг.м / с
Теперь длина волны электрона
λ =h/√2mE
= 6.62 * 10-34/ 5.7 * 10-24
= 4.8 * 10-10m
=48нм
Длина волны электрона, движущегося со скоростью 6.35*106м/с составляет 48 нм.
Q2. Черный объект площадью 180 кв.м находится при температуре 550К. Какова скорость излучения энергии от объекта?
Данный: А=180 кв.м
Т=550К
Поскольку объект имеет черный цвет, коэффициент излучения равен 1.
е =1
У нас есть,
U=ɛΣT4A
=1*с 5.67* 10-8* 5504* 180
= 0.93 * 106МОЩНОСТЬ
Мощность излучения от выброса излучения от объекта составляет 0.93*106Вт.
Какова абсолютная температура системы?
Это неизменное и совершенное значение температуры системы.
Абсолютная температура системы измеряется по шкале градусов Цельсия, Фаренгейта или Кельвина, которые измеряют ноль как абсолютный ноль градусов.
Как длина волны фотона зависит от температуры?
Температура системы определяет подвижность частиц системы.
Чем больше излучений получает система при более высоких температурах, тем больше излучения будет излучаться системой. При более высоких температурах излучаются более короткие волны, а при более низких температурах излучаются более длинные волны.
Как определить длину волны де Бройля для электрона
Содержание:
- Волна де Бройля или волна амплитуды вероятности
- Природа волн де Бройля, фазовая и групповая скорость
- Какой формулой определяется длина волны
- Как определить длину волны де Бройля для электрона
Волна де Бройля или волна амплитуды вероятности
Волна де Бройля является волной вероятности или волной амплитуды вероятности, которая определяет плотность вероятности обнаружения объекта в конкретной точке конфигурационного пространства.
Согласно определения волн де Бройля, можно сделать вывод об их взаимодействии с какими-либо частицами и их волновой природе. Формулировка волн материи была введена в науку в 1924 году французским физиком-теоретиком Луи де Бройлем. Благодаря теории, свойство корпускулярно-волнового дуализма (или двойственности) было распространено на любые проявления материи, включая излучение и какие-либо частицы вещества.
В современной квантовой теории «волна материи» понимается несколько иначе. Однако название данного физического феномена, связанного с частицами вещества, включая водород, сформулировано в честь автора гипотезы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В 1913 году Н. Бор предложил полуклассическую модель атома, в основе которой было два постулата:
- Момент импульса электрона в атоме строго определен. Величина в любом случае пропорциональна nh/2π, где n – какое-либо целое число, начиная с 1, а h – постоянная Планка, присутствие которой в формуле ясно свидетельствует о том, что момент импульса частицы квантован. Таким образом, атом включает комплекс разрешенных орбит, по которым только и может перемещаться электрон. Когда электрон расположен на этих орбитах, излучение (то есть потеря энергии) отсутствует.
- Атомный электрон излучает или поглощает энергию в процессе перехода с одной орбиты на другую в количестве, определяемом, как разность энергий на этих орбитах. В связи с тем, что промежуточные состояния между разрешенными орбитами отсутствуют, излучение строго квантуется. Показатель его частоты составляет (E1 – E2)/h, что является выводом из формулы Планка для энергии E = hν.
Таким образом, боровская модель атома не предусматривает излучение электрона на орбите, его нахождение между орбитами. Однако согласно простой рассматриваемой модели, движение электрона рассматривают с классической точки зрения, как вращение планеты вокруг Солнца.
В процессе поиска ответа на вопрос о поведении электрона Де Бройль предположил, что электрону в любом случае должна соответствовать определенная волна. Благодаря ей, частица «выбирает» исключительно такие орбиты, на которых данная волна укладывается целое число раз. В этом и заключался смысл целочисленного коэффициента в постулированной Бором формуле.
Гипотеза приводит к выводу, что электронная волна де Бройля не является электромагнитной, а волновые параметры должны быть характерны для любых материальных частиц, а не только для электронов в атоме. Ученому удалось получить важное соотношение, с помощью которого можно определить тип этих рассматриваемых волновых свойств. Формула расчета волны де Бройля:
(λ = h/p)
где λ – является длиной волны, p – определяет импульс частицы в уравнении.
Де Бройль объединил в одном соотношении корпускулярную и волновую характеристики материи: такие, как импульс и длина волны. Данные параметры связывает постоянная Планка, величина которой примерно составляет (6,626*10^{-27} эрг∙с) или (6,626*10^{-34} Дж∙с), задающая масштаб проявления волновых свойств вещества.
Природа волн де Бройля, фазовая и групповая скорость
Следует отметить, что волны де Бройля, называемые электронными волнами, не являются электромагнитными. В 1927 году американским физикам Дэвиссону и Джермеру удалось подтвердить гипотезу де Бройля. Ученые обнаружили дифракцию электронов на кристалле никеля. В процессе получилось определить дифракционные максимумы, которые соответствуют формуле Вульфа-Брэггов:
(2dsinj = nl)
Расчет брэгговской длины волны подтвердил ее соответствие формуле:
В дальнейшем гипотеза де Бройля была подтверждена опытным путем Л.С. Тартаковским и Г. Томсоном. Ученым удалось зафиксировать дифракционную картину, когда пучок быстрых электронов при Е≈ 50 кэВ проходит сквозь фольгу из разных металлов.
Чуть позже получилось обнаружить дифракцию нейтронов, протонов, атомных пучков и молекулярных пучков. В дальнейшем были изобретены инновационные методики исследования вещества, включая нейтронографию и электронографию, сформировалось направление электронной оптики.
Макротела должны характеризоваться аналогичными свойствами. В случае, если m = 1кг, (l = 6,62*10^{-31} м) – невозможно обнаружить современными методами – поэтому макротела рассматриваются только в качестве корпускул.
В том случае, когда частица с массой m перемещается со скоростью v, фазовая скорость волн де Бройля будет определяться по формуле:
Исходя из того, что c > v, фазовая скорость волн де Бройля превышает скорость света в вакууме. Можно отметить, что фазовая скорость Vф может быть больше и может быть меньше с, в отличие от групповой скорости. Формула групповой скорости:
Таким образом, групповая скорость волн де Бройля соответствует скорости движения частицы. В случае фотона она будет равна:
В результате, значение групповой скорости равно скорости света.
Волны де Бройля подвержены дисперсии. Если подставить выражение:
в формулу:
получим следующее равенство:
(Vф= f(λ))
Примечание
Так как присутствует дисперсия, волны де Бройля невозможно представить, как волновой пакет. В противном случае, он мгновенно «расплывется», то есть исчезнет, в течение 10-26 с.
Какой формулой определяется длина волны
Количественные соотношения, которые связывают корпускулярные и волновые способности частиц, аналогичны свойствам фотонов:
Гипотеза де Бройля основана на универсальном характере данного равенства, что справедливо в условиях любых волновых процессов. Какой-либо частице, которая обладает импульсом р, соответствует волна. Ее длину можно определить с помощью формулы де Бройля:
p =mv– является импульсом частицы, h – определяется, как постоянная Планка.
Как определить длину волны де Бройля для электрона
Рассчитать длину волны де Бройля для электрона можно на конкретном примере. Предположим, то требуется определить длину волны де Бройля λ для электрона, кинетическая энергия которого составляет:
- W1 = 10 кэВ;
- W2 = 1 МэВ.
В первую очередь стоит записать исходные данные:
(m_{e}=9,1*10^{-31} кг)
(W1 = 10 кэВ = 10*10^{3}*1,6*10^{-19} = 1,6*10^{-15}Дж)
(W2 = 1 МэВ = 10*10^{6}*1,6*10^{-19}= 1,6*10^{-13} Дж)
Требуется найти λ.
Решение:
Формула волны де Бройля:
Так как известна кинетическая энергия электронов, можно рассчитать их скорость:
Далее можно определить длину волны де Бройля:
В том случае, когда скорость v частиц соизмерима со скоростью света с, длину волны де Бройля можно рассчитать по формуле:
где длине волны
соответствует максимальное значение
спектральной плотности энергетической
светимости абсолютно черного тела,
– постоянная Вина.
Квантовая гипотеза
Планка устанавливает пропорциональность
между энергией кванта излучения и
частотой колебаний
,
где
– постоянная Планка.
Формула Планка
для спектральной плотности энергетической
светимости абсолютно черного тела имеет
вид
.
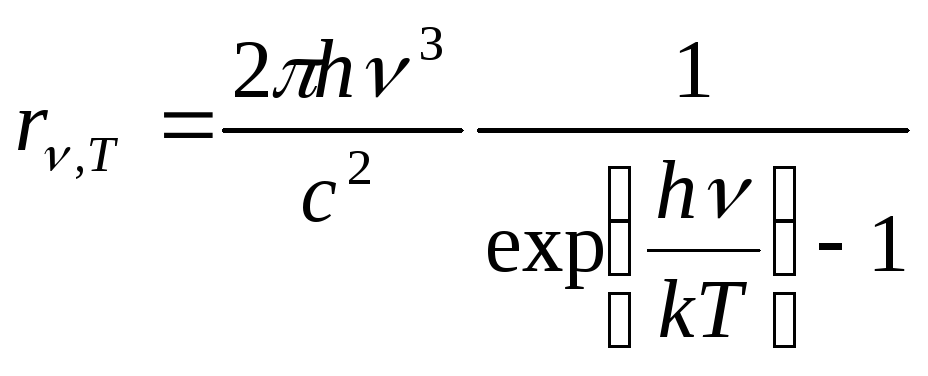Уравнение Эйнштейна
для внешнего фотоэффекта
,
где
– работа выхода электрона из металла,
– максимальная кинетическая энергия
электрона.
Красная граница
фотоэффекта может быть определена по
формулам
,
.
Величина запирающего
напряжения вычисляется по формуле
.
Масса фотона
определяется при помощи формул Планка
и Эйнштейна
,
а его импульс равен
.
Давление света,
падающего нормально на некоторую
поверхность, определяется по формуле
,
где
– энергия всех фотонов, падающих на
единицу площади поверхности за единицу
времени (энергетическая освещенность
поверхности),
– коэффициент отражения света от
поверхности,
– объемная плотность энергии излучения.
Изменение длины
волны коротковолнового излучения при
его рассеянии на свободных (или
слабосвязанных) электронах (эффект
Комптона) определяется по формуле
,
где
– угол рассеяния,
– комптоновская длина волны (для рассеяния
фотона на электроне
).
Длина волны
коротковолновой границы сплошного
рентгеновского спектра определяется
по формуле
,
где
– напряжение на рентгеновской трубке.
Примеры решения задач
Задача 1. Излучение
Солнца близко по своему спектральному
составу к излучению абсолютно черного
тела, для которого максимум испускательной
способности приходится на длину волны
.
Найти массу, теряемую Солнцем ежесекундно
за счет излучения. Оценить время, за
которое масса Солнца уменьшится на 1%.
Решение
Воспользуемся
законом смещения Вина и определим
температуру поверхности Солнца
.
(2.1.1)
Тогда энергетическая
светимость Солнца по закону Стефана –
Больцмана и при помощи (2.1.1) запишется
в виде
.
(2.1.2)
Умножая (2.1.2) на
площадь излучающей поверхности и время,
находим энергию, излучаемую Солнцем
.
(2.1.3)
Для определения
массы, теряемой Солнцем вследствие
излучения, воспользуемся формулой
Эйнштейна для взаимосвязи массы и
энергии, что с учетом (2.1.3) позволит
записать
.
(2.1.4)
Учитывая, что
площадь излучающей поверхности (сферы)
,
из (2.1.4) находим
Чтобы оценить
время уменьшения массы Солнца на 1%,
предположим, что в течение этого времени
энергия, излучаемая Солнцем, не изменяется,
тогда
.
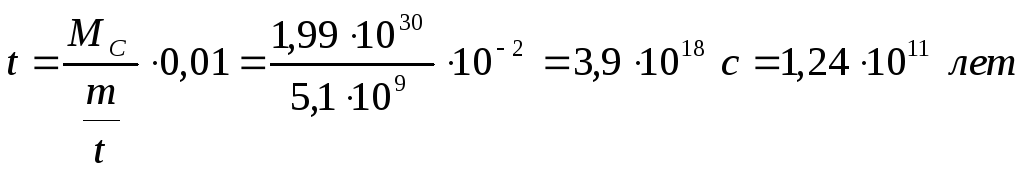Задача 2. Определить
установившуюся температуру
зачерненного шарика, расположенного
на половине расстояния от Земли до
Солнца. Температуру поверхности Солнца
принять равной
.
Решение
Очевидно, что
находясь в состоянии теплового равновесия,
шарик должен получать в единицу времени
такую же энергию излучения от Солнца,
которую сам излучает в окружающее
пространство. Тогда, обозначая мощность
солнечного излучения, упавшего на шарик
через
,
а мощность, излученную шариком – через
,
имеем
.
(2.1.5)
Предполагая, что
Солнце излучает как абсолютно черное
тело, выражение для мощности солнечного
излучения можно записать в виде
,
(2.1.6)
где
– температура поверхности Солнца,
– площадь поверхности Солнца. Долю
мощности солнечного излучения,
приходящуюся на поверхность шарика,
найдем из пропорции
,
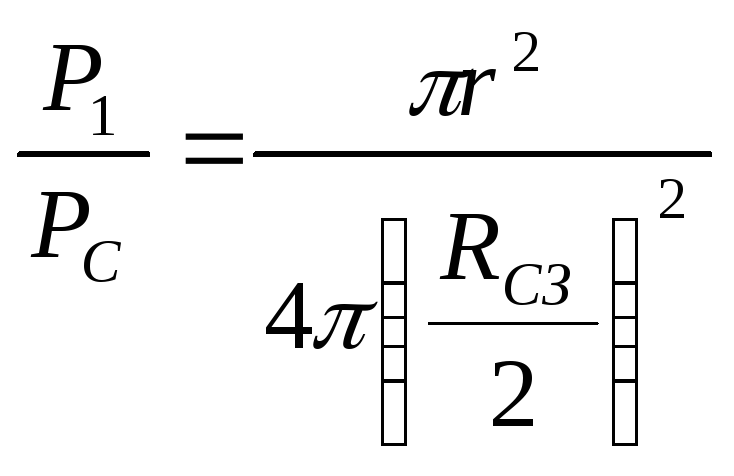(2.1.7)
где
– площадь круга радиуса
,
равного радиусу шарика,
– расстояние от Земли до Солнца. Из
(2.1.6), (2.1.7) находим
.
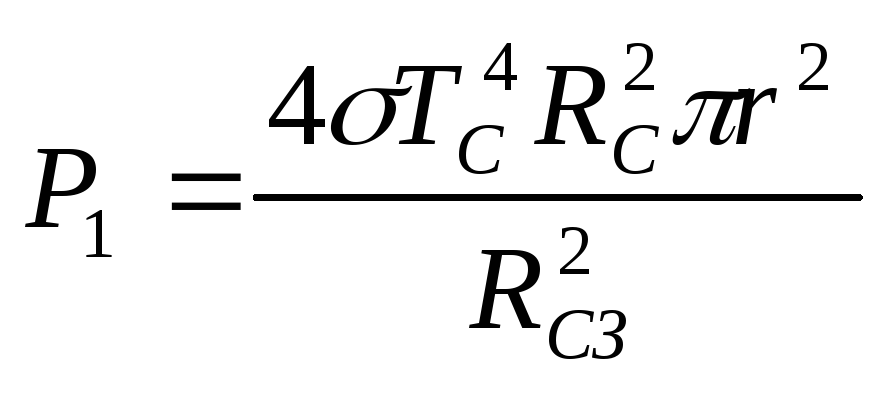(2.1.8)
Определим теперь
мощность излучения шарика, предполагая,
что он тоже излучает как абсолютно
черное тело, а температура всех его
точек одинакова. Тогда получим
.
(2.1.9)
Из (2.1.5), (2.1.8), (2.1.9)
следует
.
Используя табличные
данные, получаем ответ
.
Задача 3. Медный
шарик, удаленный от других тел, под
действием света, падающего на него,
зарядился до потенциала
.
Определить длину волны света.
Решение
Согласно уравнению
Эйнштейна для фотоэффекта максимальная
кинетическая энергия фотоэлектронов
равна
.
(2.1.10)
Вследствие вылета
электронов с шарика под действием света
он приобретает положительный заряд, в
результате чего вокруг него создается
электрическое поле, тормозящее движение
вылетевших электронов. Шарик будет
заряжаться до тех пор, пока максимальная
кинетическая энергия фотоэлектронов
не станет равной работе тормозящего
электрического поля при перемещении
электронов на бесконечно большое
расстояние. Так как потенциал бесконечно
удаленной точки равен нулю, по теореме
о кинетической энергии получаем
,
что с учетом
(2.1.10) позволяет найти длину волны света
.
(2.1.11)
Подставляя в
(2.1.11) числовые значения (работа выхода
электронов из меди равна
),
находим
.
Задача 4. Плоская
поверхность освещается светом с длиной
волны
.
Красная граница фотоэффекта для данного
вещества
.
Непосредственно у поверхности создано
однородное магнитное поле с индукцией
,
линии которого параллельны поверхности.
На какое максимальное расстояние от
поверхности смогут удалиться фотоэлектроны,
если они вылетают перпендикулярно
поверхности?
Решение
Воспользуемся
уравнением Эйнштейна для фотоэффекта
и определим максимальную скорость
вылетающих фотоэлектронов
.
(2.1.12)
Используя формулу
для красной границы фотоэффекта
,
выражение (2.1.12)
можно записать в виде
.
(2.1.13)
После вылета с
поверхности электроны попадает в
перпендикулярное к вектору скорости
однородное магнитное поле, следовательно,
движутся в нем по окружности, и их
максимальное удаление от поверхности
будет равно радиусу этой окружности.
Радиус окружности можно найти, применяя
второй закон Ньютона и используя формулу
Силы Лоренца
.
(2.1.14)
Тогда из (2.1.13),
(2.1.14) находим максимальное удаление
электронов от поверхности
.
Вычисления дают
.
Задача 5. Катод
фотоэлемента освещают монохроматическим
светом. При задерживающем напряжении
между катодом и анодом
ток в цепи прекращается. При изменении
длины волны света в
раза потребовалось подать на электроды
задерживающую разность потенциалов
.
Определить работу выхода электронов
из материала катода.
Решение
Используя уравнение
Эйнштейна для фотоэффекта и формулу
для задерживающего напряжения, получаем
,
(2.1.15)
,
(2.1.16)
где длины волн
связаны условием
.
(2.1.17)
Решая систему
уравнений (2.1.15) – (2.1.17), находим
.
Задача 6. Определить,
с какой скоростью должен двигаться
электрон, чтобы его импульс был равен
импульсу фотона с длиной волны
.
Решение
Предварительно
сравним энергию фотона с энергией покоя
электрона
,
.
Вычисления
показывают, что энергия фотона больше
энергии покоя электрона, следовательно,
при решении задачи необходимо использовать
формулы специальной теории относительности.
Приравнивая формулы импульса фотона и
релятивистского электрона, получаем
.
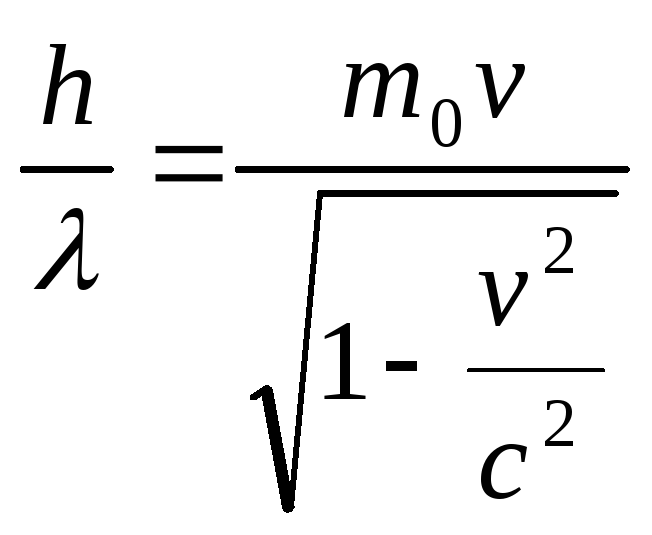(2.1.18)
Решая (2.1.18)
относительно скорости электрона,
получаем
.
Задача 7. В космосе
движется пылинка плотностью
,
поглощающая весь падающий на нее свет.
Зная мощность излучения Солнца
,
найти радиус пылинки, при котором ее
гравитационное притяжение к Солнцу
компенсируется силой светового давления.
Решение
Согласно условию
задачи сила всемирного тяготения должна
уравновешиваться силой светового
давления, поэтому
.
(2.1.19)
По закону всемирного
тяготения
,
(2.1.20)
где массу пылинки
можно записать в виде
;
(2.1.21)
здесь
– радиус пылинки,
– расстояние от пылинки до Солнца.
Сила светового
давления равна
,
(2.1.22)
где проекция
поверхности пылинки на плоскость,
перпендикулярную солнечным лучам, имеет
площадь
,
(2.1.23)
а давление связано
с мощностью излучения
,
пронизывающего поверхность пылинки
формулой
.
(2.1.24)
Мощность излучения,
приходящуюся на пылинку, можно выразить
через мощность солнечного излучения
при помощи пропорции
.
(2.1.25)
Исключая из системы
(2.1.19) – (2.1.25) неизвестные, получаем
формулу для радиуса пылинки
.
Подстановка
числовых значений дает
.
Задача 8. В результате
столкновения фотона и протона, летевших
по взаимно перпендикулярным направлениям,
протон остановился, а длина волны фотона
изменилась на
.
Чему был равен импульс фотона? Скорость
протона считать
.
Решение
Воспользуемся для
решения задачи законами сохранения
импульса и энергии. Пусть первоначальный
импульс фотона
направлен по оси
,
импульс протона
– по оси
,
а импульс фотона после рассеяния
образует с осью
угол
(рис. 2.1.1). Учитывая, что движение протона
по условию можно описывать классическими
формулами, по закону сохранения энергии
имеем
.
(2.1.26)
Р
ис.
2.1.1
Закон сохранения
импульса в проекциях на оси
и
дает
,
.
(2.1.27)
Изменение длины
волны рассеянного фотона по условию
удовлетворяет формуле
.
(2.1.28)
Выразим из (2.1.27)
и
,
возведем эти уравнения в квадрат, сложим
и воспользуемся основным тригонометрическим
тождеством. В результате получим
.
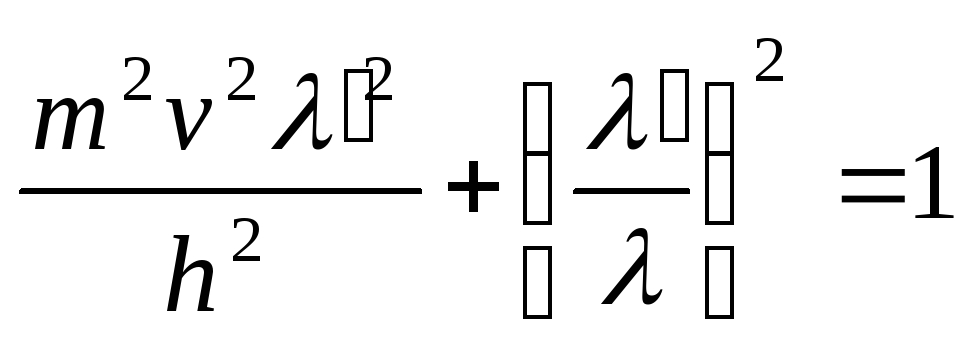(2.1.29)
Исключая из
(2.1.26), (2.1.29)
при помощи (2.1.28), преобразуем эти уравнения
к виду
,
(2.1.30)
.
(2.1.31)
Исключая теперь
из системы (2.1.30), (2.1.31) скорость протона,
находим длину волны фотона до рассеяния
,
после чего определяем
первоначальный импульс фотона
.
Задача 9. Узкий
пучок монохроматического рентгеновского
излучения падает на рассеивающее
вещество. При этом длины волн смещенных
составляющих излучения, рассеянного
под углами
и
,
отличаются друг от друга в
раза. Считая, что рассеяние происходит
на свободных электронах, найти длину
волны падающего излучения.
Решение
Воспользуемся
формулами изменения длины волны при
комптоновском рассеянии для двух углов
рассеяния, упомянутых в условии
,
.
(2.1.32)
Деля второе
уравнение (2.1.32) на первое, получаем
.
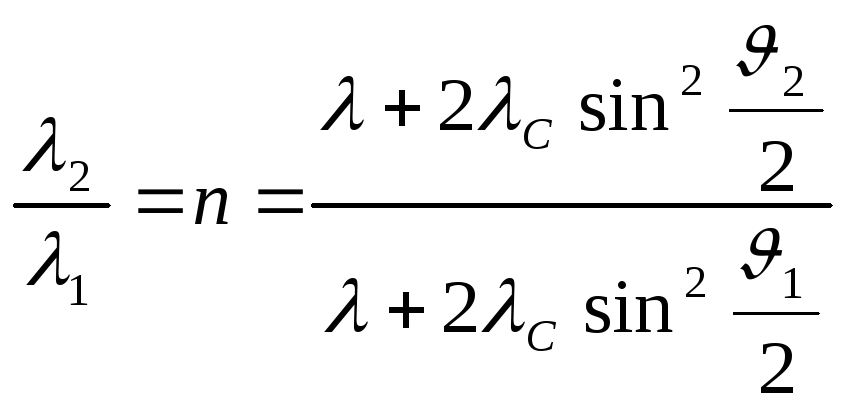(2.1.33)
Решая (2.1.33), находим
длину волны падающего на вещество
излучения
.
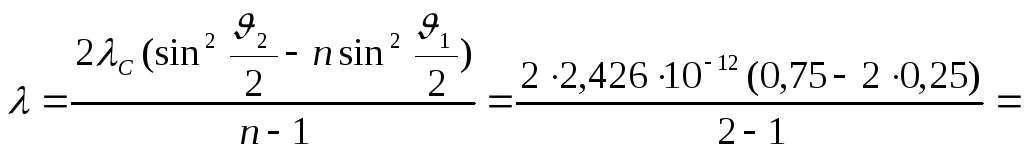
Задача 10. Фотон с
энергией, в
раза превышающей энергию покоя электрона,
рассеялся назад на неподвижном свободном
электроне. Найти радиус кривизны
траектории электрона отдачи в магнитном
поле с индукцией
,
предполагая, что линии индукции
перпендикулярны вектору скорости
электрона.
Решение
Запишем выражение
изменения длины волны света при
комптоновском рассеянии
.
(2.1.34)
Перейдем в (2.1.34)
от длин волн к энергиям при помощи
соотношения
и учтем, что угол рассеяния
.
В результате получим
,
(2.1.35)
где
– энергия покоя электрона. С учетом того,
что
,
находим из (2.1.35) энергию рассеянного
фотона
и кинетическую
энергию электрона отдачи
.
(2.1.36)
Как известно,
радиус окружности, по которой электрон
движется в магнитном поле, определяется
по формуле
,
(2.1.37)
где с учетом
релятивистского характера движения
электрона
.
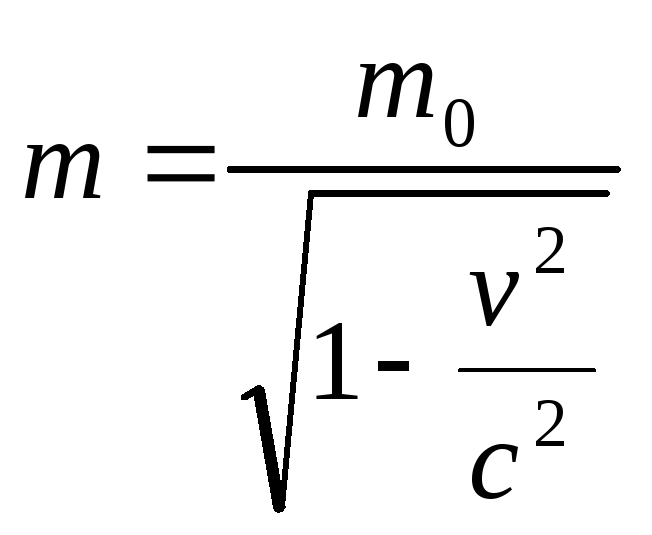(2.1.38)
Используя
релятивистскую формулу кинетической
энергии
,
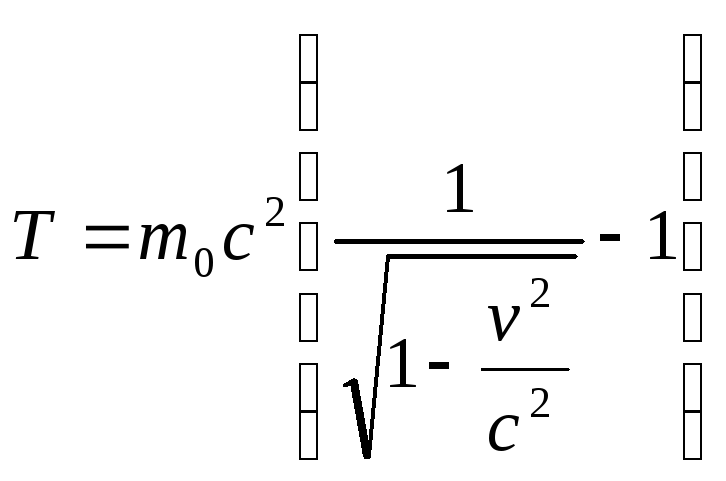из (2.1.36) после
алгебраических преобразований можно
получить
,
что после подстановки
в (2.1.37), (2.1.38) позволяет найти радиус
кривизны траектории электрона
.
(2.1.39)
Подстановка в
(2.1.39) числовых значений дает
.
Задача 11. При
увеличении напряжения на рентгеновской
трубке в
раза длина волны коротковолновой границы
сплошного рентгеновского спектра
изменилась на
.
Найти первоначальное напряжение на
трубке.
Решение
Применим формулу
длины волны коротковолновой границы
сплошного рентгеновского спектра для
случаев до и после изменения напряжения
на трубке
,
.
(2.1.40)
Вычитая из первого
уравнения (2.1.40) второе, находим
,
откуда следует
формула первоначального напряжения на
трубке
.
