Как найти скорость электрона в конденсаторе

Решение.
На электрон который находится в плоском конденсаторе действует сила Кулона, сила Кулона сообщает электрону ускорение.

[ {{F}_{K}}=mcdot a(1),{{F}_{K}}=qcdot E(2),d=frac{{{upsilon }^{2}}-upsilon _{0}^{2}}{2cdot a}(3),C=frac{varepsilon cdot {{varepsilon }_{0}}cdot S}{d}(4).
 ]

Где: m – масса электрона, m = 9,1∙10^-31 кг, q = 1,6∙10^-19 Кл, q – модуль заряда электрона, ε = 1,0 – диэлектрическая проницаемость вакуума, ε₀ = 8,854∙10^-12 Ф/м – электрическая постоянная, d – расстояние между пластинами.
Из (4) выразим d расстояние между пластинами и подставим в (3), из (3) выразим ускорение, (2) и (3) подставим в (1) определим скорость электрона.

[ begin{align}
  & d=frac{varepsilon cdot {{varepsilon }_{0}}cdot S}{C},frac{varepsilon cdot {{varepsilon }_{0}}cdot S}{C}=frac{{{upsilon }^{2}}}{2cdot a},a=frac{{{upsilon }^{2}}cdot C}{2cdot varepsilon cdot {{varepsilon }_{0}}cdot S},qcdot E=mcdot frac{{{upsilon }^{2}}cdot C}{2cdot varepsilon cdot {{varepsilon }_{0}}cdot S}, \
 & upsilon =sqrt{frac{qcdot Ecdot 2cdot varepsilon cdot {{varepsilon }_{0}}cdot S}{mcdot C}}(5). \
end{align} ]

Спрятать решение

Источник: Гельф­гат И. М. Сбор­ник задач по фи­зи­ке для 10 клас­са, Х.: «Гим­на­зия», 2001 (№ 14.24)

Электрон влетает в
пространство между обкладками плоского воздушного конденсатора под α к нижней
обкладке. Определите минимальное значение модуля скорости электрона, при
которой он достигнет верхней обкладки конденсатора, если напряжение между
обкладками 60 В.

Решение.

Предположим, что
обкладки конденсатора покоятся относительно инерциальной системы отсчета,
связанной с лабораторией, и расположены горизонтально. Ось OX направим вдоль нижней обкладки конденсатора, ось OY –
вертикально вверх. Отсчет времени начнем в момент влета электрона в пространство
между обкладками конденсатора.

В качестве физической
системы рассмотрим «электрон». Будем считать его материальной точкой.
Выделенная система не замкнута, поэтому для решения задачи воспользуемся
кинематико-динамическим способом описания.

Движущийся в
пространстве между обкладками конденсатора электрон взаимодействует с
электростатическим полем конденсатора, с гравитационным и магнитным полями
Земли и с воздухом. Взаимодействие электрона с электростатическим полем можно
описать силой F_эл = eE, модуль которой, если пренебречь краевыми эффектами и явлением
электростатической индукции, не изменяется. Эта сила направлена против поля
(заряд электрона отрицательный). Взаимодействие электрона с гравитационным
полем Земли можно описать силой тяжести mg.
Если взаимодействием с воздухом и с магнитным полем пренебречь, то динамическое
уравнение движения электрона имеет вид: ma
= mg + eE. Принимая во внимание, что F_эл >> mg , получим ma = eE, т.е. движение электрона будет равноускоренным. Поэтому
кинематические законы движения электрона имеют следующий вид.

Проецируем векторы,
изображающее соответствующие величины, на оси координат.

Решив данную систему
уравнений относительно v₀ , с учетом того, что E
= U/d, где d
– расстояние между обкладками
конденсатора, получим v₀ .

Так как все величины,
входящие в формулу, за исключением v_y
, постоянны, то v₀ = f(v_y). Вертикальная составляющая скорости электрона у верхней
обкладки должна удовлетворять условию v_y
>= 0, т.е. в противном случае электрон
повернет обратно, так и не долетев до нее. Поэтому скорость влета электрона в
конденсатор будет минимальной, если v_y
= 0.

Задачу можно решить,
применив к рассматриваемой физической системы теорему об изменении кинетической
энергии, согласно которой изменение кинетической энергии электрона при перемещений
из начального состояния в конечное в электростатическом поле конденсатора равно
работе внешних сил, действовавших на него во время движения. При сделанных допущениях
DW_кин = A_{эл.поля} . если в качестве
начального состояния физической системы выбрать состояние в момент влета
электрона в конденсатор, а в качестве конечного – момент подлета к верхней
обкладки, то получаем.

Работа сил
электростатического поля A = –eU.

Так как v_y >= 0, то получаем такую же самую формулу как и в первом
случае.

Этот же результат можно
получить, рассмотрев физическую систему «электрон – электрической поле
конденсатора», которая, если пренебречь взаимодействием с внешними объектами,
является замкнутой и  может быть описана
законом сохранений энергии, в соответствии с которым энергия системы в момент
влета электрона в конденсатор равна ее энергии в тот момент времени, когда
электрон окажется у верхней обкладки.

Выбираем нулевой
уровень потенциала на верхней обкладке конденсатора.

Где eU –
потенциальная энергия взаимодействия электрона с электростатическим полем
конденсатора. Энергия системы в конечном состоянии – W­_кон .

Таким образом,
использование различных вариантов теоретического базиса решения задачи и
различный выбор физических систем приводят к одному и тому же результату, что
свидетельствует о правильности ее решения.

Заметим, что полученное
значение v_0min
является ответом задачи при условии, что
угол α удовлетворяет условию α >= arctg 2d/l.

Ответ: 

Источник: Физика. Полный курс подготовки к ЦТ.  Под общей редакцией проф. В.А. Яковенко.

ЭЛЕКТРИЧЕСТВО
И МАГНЕТИЗМ

________________________________________________________________

Лабораторная
работа №
301

ДВИЖЕНИЕ ЗАРЯДА
В ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Цель работы:

• экспериментальное
  исследование закономерностей движения
  точечного заряда в однородном
  электрическом поле

• экспериментальное
  определение величины удельного заряда
  частиц.

Приборы и
принадлежности:

• персональный
  компьютер

• компьютерные
  модели «Открытая физика 1.1».

Краткая теория

Движение заряженных
частиц в электрическом поле широко
используется в современных электронных
приборах, в частности, в электронно-лучевых
трубках с электростатической системой
отклонения электронного пучка.

Электрический
заряд– характеристика элементарной
частицы, которая определяет величину
электромагнитного взаимодействия. В
Международной системе единиц (СИ) единица
измерения заряда –кулон
(Кл).

Существуют
два рода электрических зарядов:
положительные и
отрицательные.
Одноимённо заряженные тела отталкиваются
друг от друга, а разноименные притягиваются
друг к другу.

Основной
закон взаимодействия точечных зарядов
(закон Кулона):

Сила
электростатического взаимодействия

(сила
Кулона) между двумя
точечными зарядами
ипрямо пропорциональна
произведению величин зарядов и обратно
пропорциональна квадрату расстояния


между ними:

,
(1)

где
–
коэффициент пропорциональности (для
взаимодействия частиц в вакууму),r– расстояние между
двумя точечными зарядамиq₁иq₂,–
радиус – вектор, соединяющий зарядq₂
с зарядом q₁.
Точечным электрическим зарядомназывается заряженное тело, линейные
размеры которого несущественны в данной
задаче.

Пространство, в
котором находится электрический заряд,
обладает тем свойством, что на внесённый
в него другой заряд действует сила
Кулона. Следовательно, в пространстве,
окружающем электрические заряды,
существует силовое поле, которое
называется электромагнитным полем.Электромагнитное поле– особый вид
материи, посредством которой осуществляется
взаимодействие между электрическими
заряженными частицами.

Электростатическое
поле– это частный вид электромагнитного
поля. Оно создается совокупностью
электрических зарядов, неподвижных в
пространстве и неизменных во времени.

Основными величинами,
характеризующими электростатическое
поле, являются напряженность (силовая
характеристика поля) ипотенциал
(энергетическая характеристика поля).

Потенциал поляв некоторой точке пространства численно
равен работе, совершаемой силами
электростатического поля над единичным
положительным зарядомпри удалении его из данной точки в
бесконечность, т. е.

.
(2)

Работа, совершаемая
полем по перемещению заряда, равна
изменению потенциальной энергии заряда,
т.е.

откуда следует,
что потенциальная энергия заряда
в поле зарядаравна

,

а потенциал

.

Потенциал
электрического поля– скалярная
величина, равная отношению потенциальной
энергии заряда в поле к величине
единичного положительного заряда.

В Международной
системе единиц (СИ) потенциал измеряется
в вольтах (В).

Напряженность
электрического поля– векторная
величина, определяющаяся отношением
силы,
действующей со стороны поля на неподвижный
пробный положительный точечный
электрический зарядапомещенный в рассматриваемую точку
поля, к величине этого заряда:

,
(3)

где
– электрическая постоянная,–
диэлектрическая проницаемость среды
– она показывает, на сколько сила
взаимодействия между двумя точечными
зарядами в данной среде. В Международной
системе единиц (СИ) физических величин
напряженность измеряется в

Графически
электростатическое поле изображают с
помощью силовых линий (линий
напряженности).Силовой линиейназывается линия, касательная к которой
в каждой точке поля совпадает с
направлением вектора напряженности.

Различают однородные
и неоднородные электрические поля.
Напряженность
во всех точках однородного поля имеет
одно и тоже значение и его силовые линии
параллельны. Примером однородного
электрического поля является полеплоского конденсатора(исключая
края конденсатора).

Конденсатор –
устройство, способное накапливать
электрический заряд, состоящее из двух
изолированных друг от друга проводников.
Независимо от формы проводников их
называют пластинами конденсатора.

Простейшим
конденсатором является плоский
конденсатор,
состоящий из двух плоскопараллельных
металлических пластин, линейные размеры
которых много больше расстояния между
ними.

В неоднородном
электрическом поле напряженность
меняется от точки к точке (поле точечного
заряда, диполя).

Работа
по перемещению заряда q
из одной точки
пространства в другую вдоль координатной
оси x
при условии, что точки расположены
бесконечно близко друг к другу и
,
равна

.
(4)

С
другой стороны, работа по перемещению
заряда равна произведению этого заряда
на разность потенциалов в начальной и
конечной точках пути:

.
(5)

Приравнивая
выражения (4) и (5), получим:

,

или

.
(6)

Аналогичные
выражения можно получит для осей
декартовых координат y,
z.

Учитывая, что
градиентом скалярной величиныявляется вектор, показывающий направление
наибольшего изменения этой величины в
пространстве, получаем выражение

.
(7)

Уравнение (7)
связывает между собой силовую и
энергетическую характеристики
электрического поля. Знак “– ” в
выражении (7) указывает на то, что
напряженность электрического поля
направлена в сторону убывания его
потенциала.

Для графического
изображения распределения потенциала
электростатического поля используют
эквипотенциальные поверхности–
поверхности, во всех точках которых
потенциалимеет одно и то же значение.

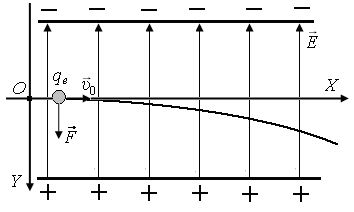
Рассмотрим движение
отрицательного элементарного заряда
(электрона) в однородном электрическом
поле (в поле плоского конденсатора)
(рис. 1).

Рис.1. Движение электрона в поле плоского конденсатора

На
заряд q_e,
находящийся в электрическом поле
плоского конденсатора с напряженностью
,
действует электрическая сила

,

где q_е
– заряд электрона. Под действием
этой силы электрон двигается относительно
горизонтально расположенных пластин
конденсатора с ускорением.
Согласно второму закону Ньютона:

,
(8)

где m– масса электрона,–
ускорение электрона..

Движение электрона
внутри конденсатора является суперпозицией
двух движений: 1) по инерции вдоль оси
ОХс постоянной скоростью,
где– начальная скорость движения заряда.
Кинематическое уравнение движения
заряда относительно оси ОХ

;
(9)

2) равноускоренного
движения в вертикальном направлении
(ось OY) к положительно
заряженной пластине под действием
постоянной электрической силы поля
конденсатора. Учитывая, что проекция
начальной скорости электрона на
рассматриваемую ось равна нулю (рис.
1), кинематическое уравнение движения
заряда относительно осиОY

.
(10)

При движении
электрона в конденсаторе проекция
вектора перемещения электрона на ось
ОXравна длине
конденсатораL.Тогда
из выражения (9), получим, что электрон
пролетит конденсатор за время

.
(11)

Учитывая (11),
уравнение (10) в скалярном виде будет

.
(12)

Представим
уравнение (8) в скалярном виде и получим
отношение

.
(13)

Правая часть
выражения (13) определяет величину
удельного заряда электрона.
Удельным зарядом
электрона называется
отношение заряда q_е
электрона к его массе m.

Решая совместно
уравнения (12) и (13) относительно удельного
заряда электрона, получим:

.
(14)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #