Сегодня у нас на рассмотрении вопрос касающийся электричества, а именно: с какой скоростью электроны движутся по проводам.
Думаю ни для никого не секрет, что носителями заряда в металле являются свободные электроны, которых там очень много. Если человек задастся сегодняшним вопросом, то может ответить, что скорость электронов в проводнике очень большая, сравнимая со скоростью света. Ведь как только мы переключаем выключатель, чтобы включить свет в комнате, тот в свою очередь появляется мгновенно. Можно простить обывателя за такой вывод, ведь мало кто изучал физику на серьезном уровне.
Сейчас мы с вами разберемся, где зарыта правда. Делать выводы мы будем исходя из классической теории металлов, не учитывая квантовых аспектов. В чем же суть классической теории металлов?
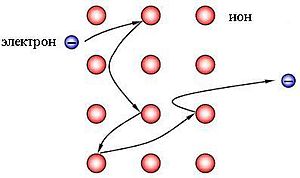
Классическую теорию металлов разработал Пауль Друде. Он предположил, что электроны проводимости в металле ведут себя словно молекулы идеального газа и в промежутках между соударениями движутся свободно. Но в отличие от молекул газа, пробег которых определяется соударениями друг с другом, электроны сталкиваются преимущественно с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронами и кристаллической решеткой.
Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, можно оценить их среднюю скорость теплового движения. Вычисляется она по следующей формуле:
Подставим все величины, температуру примем за комнатную (27 градусов Цельсия или 300 Кельвин)
И мы получаем величину хоть как-то сравнимую со скоростью света (скорость света равняется 3*10^8 м/сек). Но мы посчитали скорость их хаотического, то есть беспорядочного движения. А насколько мы знаем, электрический ток – это упорядоченное движение частиц. Поэтому я предлагаю рассчитать максимально возможную скорость упорядоченного движения электронов.
Чтобы мы могли говорить боле общо, речь вести будем не о токе, а о плотности тока. Это величина равная силе тока, которая проходит через какое-либо поперечное сечение проводника (обозначается она буквой j). Например: пусть по проводу с площадью поперечного сечения 2 мм^2 течет ток силой 1 Ампер. Тогда плотность тока в данном случае будет составлять j= 1/2 = 0,5 А/мм^2. Плотность тока вычисляется по следующей формуле:
Максимально возможная конструктивная плотность тока составляет около 10 А/мм^2, если ток выше этого значения, то медные провода просто начнут плавиться. Ну и среднее значение концентрации электронов в металле составляет около 10^23 в каждом кубическом сантиметре. Выразив все в одной системе единиц и подставив в это уравнение, найдем максимальное значение скорости упорядоченного движения:
И как вы видите она составляет всего 1 мм в секунду! Явно не по этой причине лампочка загорается так быстро. Но мы так и не ответили на вопрос: почему так происходит?
На самом деле ответ на данный вопрос, в отличие от предыдущего, довольно прост. Представьте себе огромную очередь битком набитую людьми. И пусть с конца очереди кто-то большой и массивный начал сильно толкать всех вперед. В этом случае начало очереди довольно быстро придет в движение, хоть и хулиган, который толкал всех сзади, двигался очень медленно.
Тоже самое происходит в проводах: когда электроны от источника начали свое движение, их импульс быстро, практически со скоростью света, передался электронам у приемника. Только в очереди людей вы передаете взаимодействие путем толчков, а электроны взаимодействуют при помощи электромагнитных сил.
Думаю теперь тема полностью раскрыта. Поддержите статью вашим драгоценным лайком, это очень поможет каналу! А также обязательно подписывайтесь на канал, чтобы не пропускать новых выпусков! Всего вам доброго и до скорых встреч!
Расчет тепловой скорости движения электронов
Свободные электроны в металле образуют
электронный газ. Рассчитаем скорость
беспорядочного движения электронов в
газе V, предполагая, что они подчиняются
обычным газовым законам. Тогда кинетическая
энергия движения электронов равна
![]() (18)
(18)
где me– масса электрона,
Эта энергия равна энергии теплового
движения, которая определяется абсолютной
температурой газа T
![]() (19)
(19)
где k– постоянная Больцмана.
Приравнивая (17) и (18) находим
![]() (20)
(20)
Подставив значения для комнатной
температуры t= 20oC и справочные
данныеk= 1,38*10-23Дж/К ,me=
9*10-31кг получим
![]()
Полученную скорость называют тепловой
скоростью электронов Vтепл.
Задачи для самостоятельного решения
-
Рассчитать
скорость теплового движения электронов
в проводнике электронагревательной
спирали из нихрома при температуре 600
оС
по модели электронного газа.
Справочные данные
Постоянная
Больцмана 1,38*10–23
Дж/К.
Масса
электрона 9,1*10–31
кг.
Молярная масса
никеля 59 г/моль.
-
Рассчитать
скорость теплового движения электронов
в медном проводнике, охлажденом до
температуры жидкого азота –195 оС.
Справочные данные
Постоянная
Больцмана 1,38*10–23
Дж/К.
Масса
электрона 9,1*10–31
кг.
Молярная масса
меди 64 г/моль.
Расчет электрической проводимости металлов
Запишем закон Ома
![]() (21)
(21)
Подставим в него выражение для
сопротивления проводника
![]() (22)
(22)
где l– длина проводника,S– его
сечение ,–
удельное сопротивление материала.
Тогда
![]()
или
![]() (24)
(24)
Учтя , что I / S = jесть плотность тока,U / l = Eнапряженность электрического
поля,1/ =
удельная
проводимость, получим закон Ома в
локальной формулировке
![]() (25)
(25)
Удельная проводимостьявляется свойством материала, которое,
в свою очередь, зависит от характеристик
движения электронов в металле. Найдем
эти соотношения.
Так как
![]() (26)
(26)
из (25) и (26) получим
![]() (27)
(27)
Обозначим
![]() (28)
(28)
Величина называется
подвижностью носителей заряда.
Тогда
![]() (29)
(29)
Для расчета дрейфовой скорости
электронов vдрвоспользуемся
моделью свободного движения электронов
в промежутках между столкновениями с
ионами кристаллической решетки. Среднее
время свободного движения называется
временем релаксациирел, расстояниепреодолеваемое электроном за это время
– длиной свободного пробега. Они связаны
соотношением
![]() (30)
(30)
За время движения между столкновениями,
за счет действия силы со стороны
электрического поля, электрон приобретает
импульс p
![]() (31)
(31)
с другой стороны этот импульс
пропорционален приобретенной дрейфовой
скорости
![]() (32)
(32)
Приравнивая его к (31) находим
![]() (33)
(33)
Подставим полученное выражение в (27) ,
получим
![]() (34)
(34)
или, учтя (30),
![]() (35)
(35)
В данную формулу входит неизвестная
величина длины свободного пробега . В качестве приблизительной оценки
выберем ее равной десяти периодам
кристаллической решетки металла.
![]()
Тогда подставив другие известные
величины, получим, например, для меди
величину удельной электрической
проводимости
![]()
или для удельного электрического
сопротивления
![]()
Сравнивая полученную величину с табличным
значением
![]() ,
,
видим хорошее согласие с экспериментальными
данными.
Задачи для самостоятельного решения
-
Как изменяется
длина свободного пробега электронов
в металлическом проводнике при его
нагревании? -
Во сколько раз
изменится длина свободного пробега
электронов при нагревании серебряного
проводника от 300 до 1000 К?
Удельное
электрическое сопротивление серебра
при комнатной температуре равно 0,015
Ом*м, температурный коэффициент
сопротивления составляет 4,1*10–3
К–1.
-
Почему удельное
электрическое сопротивление ферромагнитных
металлов существенно выше неферромагнитных? -
Рассчитать
электропроводность медного проводника,
приняв длину свободного пробега
электронов в металле равной 5 нм.
Справочные данные
для меди
Плотность
8,94 г/cм3
. Молярная масса 64 г/моль
Число
Авогадро 6,02*1023
моль–1.
Заряд электрона 1,6*10–19
Кл.
-
Рассчитать
электропроводность проводника из
никеля, приняв длину свободного пробега
электронов в металле равной 2 нм.
Справочные данные
для никеля:
Плотность
8,9 г/cм3
. Молярная масса 59 г/моль
Число
Авогадро 6,02*1023
моль–1.
Заряд электрона 1,6*10–19
Кл.
Соседние файлы в папке ФИЗИКА МЕТАЛЛОВ_1
- #
18.03.201522.02 Кб5вопр ФМ.xls
- #
- #
- #
- #
- #
с какой скоростью движутся электроны в металлах
Ученик
(98),
закрыт
8 лет назад
Илья
Высший разум
(359968)
8 лет назад
Электроны движутся в металле со скоростями, которые по нашим меркам являются очень высокими. Из квантовой физики (см. например, Савельев, т3, #51) известно, что средняя кинетическая энергия свободного электрона в металле составляет около 5 эВ. Вычислим среднюю скорость теплового движения электронов из формулы кинетической энергии. T=mv^2/2 => v=√(2T/m)=√(2*5*1.6*10^(-19)/9.1*10^(-31))~1.326*10^6 м/с=1326 км/с. Это не значит, что все они движутся с равной скоростью – это их усредненная скорость, среди них есть и еще более быстрые, и более медленные, и они постоянно обмениваются этой энергией, упруго сталкиваясь друг с другом.
Обычно под “скоростью электрона” ошибочно понимают скорость их упорядоченного дрейфа под действием внешнего электрического поля – когда в проводнике мы наблюдаем ток. Скорость этого дрейфа действительно очень мала и составляет порядка долей миллиметра в секунду: это похоже на то, как газ, образованный электронами хаотически движущимися с огромными скоростями, медленно-медленно перемещается в направлении вектора напряженности электрического поля.
Оценим скорость этого дрейфа. Характерный размер между атомами кристалла равен 10(-10) м. Будем считать, что каждый атом металла в кристалле находится в виде иона и один его внешний электрон всегда свободен и участвует в проводимости. В сечении проводника 1 мм^2 расположено 10^14 атомов металла, а значит, в результате дрейфа это сечение в любой момент времени пересекает 10^14 электронов. Характерная величина плотности тока в жилах кабеля имеет порядок 1А/мм^2, в эл. машинах – раз в 10 выше. При токе в 10 А сечение каждую секунду пересекает “цилиндр электронного газа” высотой 10/(10^14*19^(-19))=10^6 ангстрем=10^(-4м).
Выводы: 1. скорость хаотического движения электронов в металле имеет порядок 1000 км/с
2. Скорость упорядоченного дрейфа электронного газа в проводнике имеет порядок 0.1 мм/с в высоконагруженных проводниках электрических машин и на порядок меньше (0.01 мм/с) – в проводах и кабелях линий электропередачи.
Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. Более подробно об этом читайте далее в нашей статье.
Важно знать
Как известно, электрический ток — это упорядоченный поток носителей электрического заряда. Носители — это заряженные частицы, способные свободно перемещаться во всем объеме тела.
В случае металлов этими частицами являются электроны, которые высвобождаются при образовании связи между атомами металла.
Известно, что металлы в твердом состоянии имеют кристаллическую структуру. Частицы в кристаллах расположены в определенном порядке, образуя пространственную решетку (кристалл).
Наконец, кристаллическая решетка металла образована положительными ионами, погруженными в «облако» хаотически движущихся так называемых свободных электронов, также называемых электронами проводимости. В зависимости от валентности атомов металла, один атом может освободить от одного до трех электронов при образовании металлических связей. Число таких высвобожденных электронов непосредственно переводится в число носителей заряда. Это является одним из факторов, влияющих на способность металла проводить электрический ток.
Доказательством того, что ток в металлах вызывается электронами, послужили эксперименты наших отечественных физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американских физиков Бальфура Стюарта и Роберта Толмана.
Способность металла проводить электрический ток может быть описана физической величиной, называемой удельным электрическим сопротивлением. Эта физическая величина обозначается греческой буквой ρ (читается как «ро»). Единицей измерения удельного сопротивления является Ом · м, т.е. произведение Ом на метр. Удельное сопротивление — это константа, которая характеризует материал и имеет различные значения для разных материалов. Например, удельное сопротивление меди составляет 1.72*10-8 Ом · м. Это означает, что электрическое сопротивление медного проводника длиной 1 метр и площадью поперечного сечения 1 м равно 1.72*10-8 Ом . В целом, чем ниже удельное сопротивление материала, тем лучше он проводит электрический ток.
В таблице ниже приведены некоторые примеры удельного сопротивления часто используемых металлов.
| Металл | Удельное сопротивление (Ом · м) |
| Серебро | 1.59*10-8 |
| Медь | 1.72*10-8 |
| Алюминий | 2.82*10-8 |
| Вольфрам | 5.6*10-8 |
| Железо | 10*10-8 |
Удельное электрическое сопротивление может быть связано с микроскопическими свойствами материала. В частности, он зависит от концентрации носителей заряда и их подвижности.
Движение свободных электронов в металлах не является полностью «свободным», поскольку во время их движении они взаимодействуют с другими электронами, и прежде всего с ионами кристаллической решетки. Специфика этого движения описывается так называемой классической моделью проводимости.
Основные предположения и выводы этой модели представлены в большом упрощении ниже.
Классическая модель проводимости
Без внешнего электрического поля электроны совершают тепловые хаотические движения, сталкиваясь друг с другом, а также сталкиваясь с ионами кристаллической решетки. В результате такого движения среднее положение электронов практически не меняется (см. рис. 1.).

Из-за квантовых эффектов, и в частности из-за принципа запрета Паули, который не позволяет всем электронам занимать самое низкое энергетическое состояние, средняя скорость электронов в металлах, связанная с их хаотическим тепловым движением, больше, чем скорость частиц в классическом идеальном газе той же температуры. Она составляет порядка 10 м/с.
Если электрическое напряжение U приложено к концам проводника длиной L в нем появится электрическое поле с напряженностью E = U / L
Под действием этого внешнего поля, согласно второму закону динамики, электроны ускоряются: a = F / m,
где F = e*E — сила, с которой электрическое поле действует на электрон с зарядом e. Таким образом, ускорение электрона составляет: a = e*E / m .
Ускоренное движение электрона длится лишь довольно короткое время, пока он не столкнется с ионом
кристаллической решетки. В результате такого столкновения электрон теряет практически всю свою кинетическую энергию. Однако замедленный электрон не остается в состоянии покоя — он снова ускоряется под действием электрического поля, снова сталкивается с одним из ионов из ионы кристаллической решетки и т.д. Этот эффект добавляет к скорости тепловых движений дополнительную направленную среднюю скорость u, которая из-за отрицательного заряда электрона имеет направление, противоположное напряженности внешнего электрического поля. Эта скорость называется средней скоростью дрейфа (рис. 2).

В проводнике начинает течь электрический ток с силой тока I (см. рисунок 3).

Предполагая, что движение электрона равномерно ускоряется между столкновениями с ионами решетки, с ускорением a = e*E / m , и предполагая, что в результате столкновения электрон передает всю свою кинетическую энергию кристаллической решетке, мы можем вычислить скорость, которую развивает электрон в своем свободном движении: v = a*τ . В этой формуле τ — средний интервал времени между последующими столкновениями дрейфующего электрона с ионами кристаллической решетки.
Поскольку при равномерно ускоренном движении без начальной скорости средняя скорость является средним арифметическим начальной (равной нулю) и конечной скоростью, то получаем: u = v / 2 = e*E*τ / 2*m .
Из полученной формулы следует, что скорость дрейфа, помимо внешнего электрического поля, определяется средним интервалом времени между столкновениями электронов с ионами решетки. Этот параметр зависит от многих факторов (включая температуру, кристаллическую структуру металла, дефекты кристаллической структуры, примеси) и, как выясняется, существенно влияет на электрическое сопротивление материала.
Средняя дрейфовая скорость электронов составляет порядка 10-4 м/с. Она очень мала по сравнению со скоростью теплового движения, которая составляет порядка 106 м/с.
Классическая теория проводимости достаточно хорошо описывает явление электропроводности в металлах. Однако эта теория не может объяснить экспериментально наблюдаемую зависимость электрического сопротивления от температуры.
Причина упомянутой неудачи классической теории проводимости заключается в том, что она не учитывает влияние ионов решетки на движение электронов между столкновениями. Более близкие к реальности результаты дает квантовая теория проводимости, которая описывает электроны как частицы, подверженные квантовой статистике, движущиеся в периодическом электрическом поле, создаваемом положительными ионами решетки.
Выводы простым языком
Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален. Свободные электроны в нём движутся беспорядочно. Но если в металле создать электрическое поле, то свободные электроны начнут двигаться направленно под действием электрических сил. Возникнет электрический ток. Беспорядочное движение электронов при этом сохраняется, подобно тому как сохраняется беспорядочное движение в стайке мошкары, когда под действием ветра она перемещается в одном направлении.
« Скорость движения самих электронов в проводнике под действием электрического поля невелика — несколько миллиметров в секунду, а иногда и ещё меньше. Но как только в проводнике возникает электрическое поле, оно с огромной скоростью, близкой к скорости света в вакууме (300 000 км/c), распространяетcя по всей длине проводника. »
Перышкин А. В. Физика 8. – М.: Дрофа, 2010
Как пример, электрический сигнал, посланный, например, по проводам из Москвы во Владивосток (s = 8000 км), приходит туда примерно через 0,03 с.
Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника. Так, например, когда цепь электрической лампы замкнута, электроны в спирали лампы также движутся упорядоченно.
Сравнение электрического тока с потоком воды в водопроводной системе и распространения электрического поля с распространением давления воды поможет нам понять это. Когда вода поднимается в резервуар для воды, давление (напор) воды очень быстро распространяется по всей системе водоснабжения. Когда мы включаем кран, вода уже находится под давлением и сразу же начинает течь. Но вода, которая была в кране, течет, а вода из башни достигает крана гораздо позже, потому что вода движется с меньшей скоростью, чем распространяется давление.
Когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.
Теория Друде — классическое описание движения электронов в металлах. Эта теория была предложена немецким физиком Паулем Друде через 3 года после открытия электрона как частицы — в 1900 году. Она отличается простотой и наглядностью, хорошо поясняет эффект Холла, удельную проводимость в постоянном и переменном токе и теплопроводность в металлах и поэтому до сегодняшнего дня актуальна. Может использоваться для нескольких типов носителей включая пространственно разделённые слои как в кулоновском увлечении.
Основные предположения[править | править код]
Электроны в металле рассматриваются как электронный газ, к которому можно применить кинетическую теорию газов. Считается, что электроны, как и атомы газа в кинетической теории, представляют собой одинаковые твёрдые сферы, которые движутся по прямым линиям до тех пор, пока не столкнутся друг с другом. Предполагается, что продолжительность отдельного столкновения пренебрежимо мала, и что между молекулами не действует никаких иных сил, кроме возникающих в момент столкновения. Так как электрон — отрицательно заряженная частица, то для соблюдения условия электронейтральности в твёрдом теле также должны быть частицы другого сорта — положительно заряженные. Друде предположил, что компенсирующий положительный заряд принадлежит гораздо более тяжёлым частицам (ионам), которые он считал неподвижными. Во времена Друде не было ясно, почему в металле существуют свободные электроны и положительно заряженные ионы, и что эти ионы собой представляют. Ответы на эти вопросы смогла дать только квантовая теория твёрдого тела. Для многих веществ, однако, можно просто считать, что электронный газ составляют слабо связанные с ядром внешние валентные электроны, которые в металле «освобождаются» и получают возможность свободно передвигаться по металлу, тогда как атомные ядра с электронами внутренних оболочек (атомные остовы) остаются неизменными и играют роль неподвижных положительных ионов теории Друде.
Несмотря на то, что плотность газа электронов проводимости примерно в 1000 раз больше плотности классического газа при нормальных температуре и давлении, и несмотря на присутствие сильного электрон-электронного и электрон-ионного взаимодействия в модели Друде для рассмотрения электронного газа в металлах почти без изменений применяются методы кинетической теории нейтральных разреженных газов.
Основные предположения теории Друде.
- В интервале между столкновениями не учитывается взаимодействие электрона с другими электронами и ионами. Иными словами, принимается, что в отсутствие внешних электромагнитных полей каждый электрон движется с постоянной скоростью по прямой линии. Далее, считают, что в присутствии внешних полей электрон движется в соответствии с законами Ньютона; при этом учитывают влияние только этих полей, пренебрегая сложными дополнительными полями, порождаемыми другими электронами и ионами. Приближение, в котором пренебрегают электрон-электронным взаимодействием в промежутках между столкновениями, известно под названием приближения независимых электронов. Соответственно приближение, в котором пренебрегают электрон-ионным взаимодействием, называется приближением свободных электронов.
- В модели Друде, как и в кинетической теории, столкновения — это мгновенные события, внезапно меняющие скорость электрона. Друде связывал их с тем, что электроны отскакивают от непроницаемых сердцевин ионов (а не считал их электрон-электронными столкновениями по аналогии с доминирующим механизмом столкновений в обычном газе).
- Предполагается, что за единицу времени электрон испытывает столкновение (то есть внезапное изменение скорости) с вероятностью, равной
. Имеется в виду, что для электрона вероятность испытать столкновение в течение бесконечно малого промежутка времени
равна просто
. Время
называют временем релаксации, или временем свободного пробега; оно играет фундаментальную роль в теории проводимости металлов. Из этого предположения следует, что электрон, выбранный наугад в настоящий момент времени, будет двигаться в среднем в течение времени
до его следующего столкновения и уже двигался в среднем в течение времени
с момента предыдущего столкновения. В простейших приложениях модели Друде считают, что время релаксации
не зависит от пространственного положения электрона и его скорости.
- Предполагается, что электроны приходят в состояние теплового равновесия со своим окружением исключительно благодаря столкновениям. Считается, что столкновения поддерживают локальное термодинамическое равновесие чрезвычайно простым способом: скорость электрона сразу же после столкновения не связана с его скоростью до столкновения, а направлена случайным образом, причём её величина соответствует той температуре, которая превалирует в области, где происходило столкновение. Поэтому чем более горячей является область, где происходит столкновение, тем большей скоростью обладает электрон после столкновения.
Формула Друде[править | править код]
Кинетическое уравнение Больцмана в приближении времени релаксации приводит для проводимости электронного газа к формуле Друде:
Ниже приведён вывод этого выражения для классического случая без учёта реального потенциала рассеяния. Эта формула применима также к электронному и дырочному газу в полупроводниках (Формулу можно записать в другом виде для вырожденного электронного или дырочного газа 


Плотности состояний в двумерном проводнике
,
где gs — спиновое вырождение, gv — долинное вырождение, m* — эффективная масса и не зависит от энергии. gs = 2 а долинное вырождение для GaAs gv = 1.
Для носителей тока с параболическим законом дисперсии (энергия отсчитывается от дна зоны проводимости)
,
где νF — скорость носителей на уровне Ферми, и g = n/EF, можно получить выражение Друде для двумерно электронного газа
,
где последнее уравнение следует из условия вырожденности электронного газа и определения коэффициента диффузии.
Некоторые формулы[править | править код]
- ускорение электрона между двумя соударениями из второго закона Ньютона:
- средняя скорость электрона:
Следует, однако, иметь в виду, что мгновенная скорость электрона в металле может быть большой и определяется уровнем Ферми.
- плотность тока:
- Закон Ома:
- подвижность носителей заряда:
- тепловая энергия электрона:
Пределы применимости[править | править код]
К недостаткам этой теории следует отнести то что эта теория феноменологическая и использует время релаксации, которое нужно получить из эксперимента или более глубокой теории. Также использование кинетического уравнения Больцмана в приближении времени релаксации ограничивает применимость этой теории в области дискретного спектра носителей тока, то есть она применима только в квазиклассическом приближении, а в сильных магнитных полях (при формировании уровней Ландау) или при малом количестве мод (квантование сопротивления) не может адекватно описать физические явления. Также при макроскопическом проявлении квантовых эффектов как например явление сверхпроводимости. Даже в слабых магнитных полях теория Друде может терять применимость благодаря явлениям возникающим только в квантовой механике связанными с интерференцией, например слабая локализация, эффект Ааронова — Бома, универсальные флуктуации кондактанса. Кроме того даже сильная локализация (сильный беспорядок), перколяционная теория (низкая концентрация носителей), прыжковая проводимость и баллистический транспорт оказываются за пределами применимости этой теории.
Литература[править | править код]
- Н. Ашкрофт, Н. Мермин. Физика твердого тела: В двух томах / М.И Каганов. — М.: Мир, 1979.