…за его работы по изучению элементарного электрического заряда и фотоэлектрических явлений…
(Из решения о присуждении Нобелевской премии по физике за 1923 г. Р. А. Милликену)
…за его открытия в физической науке.
(Из решения о присуждении медали Копли, высшей награды Королевского Общества[101], Дж. Дж. Томсону)
Исследование атомных частиц
Мы знаем, что электроны, испаряющиеся из раскаленной спиральки, несут отрицательный заряд; но как измерить заряды отдельных электронов и их массы и показать, что все они одинаковы? Как измерить их скорость при вылете из электронной пушки? И потом говорят, что электроны, оторванные от молекул разреженного газа в электрической разрядной трубке, — это те самые универсальные частицы, из которых состоит материя. Как доказать, что они именно таковы? Как можно показать, что они гораздо меньше, чем атомы? Как проникнуть в атомную структуру, исследуя положительные ионы — то, что осталось от атомов в разрядной трубке? Как регистрировать ядерные снаряды (альфа- и бета-частицы), которыми стреляют радиоактивные атомы?
Электроны, ионы, ядра… Это некоторые из крошечных частиц, изучаемых современной физикой; мы описываем их индивидуальные особенности, определяя их заряд, массу, скорость… Их нужно ловить на лету. Остановившись, они затеряются среди атомов стенок приборов, проводов и т. д.[102] Поэтому нужную информацию мы добываем, отклоняя их от первоначального направления с помощью полей — точно так же, как можно оценить скорость мячика по тому, как влияет на его полет поле тяготения. Гравитационные поля слишком слабы для изучения атомных частиц. Конечно, все эти частицы, когда летят, подвергаются действию силы тяжести, но при любом разумно выбранном напряжении электронной пушки они движутся слишком быстро, для того чтобы их падение можно было заметить на тех расстояниях, которые им обычно приходится пролетать. (Альфа-частица, испущенная радием, пролетев километр, сдвинулась бы под действием тяготения за это время на несколько миллионных долей сантиметра, а электроны в телевизионной трубке на таком же пути — на десятимиллионную долю сантиметра, если бы у нас была трубка в километр длиной.) Поэтому мы заставляем действовать на электрический заряд, который несут эти частицы, электрическое и магнитное поля.
В этой главе мы покажем, что можно сделать с помощью электрических полей, а в следующей главе вернемся к магнитным полям и увидим, как, объединяя действия полей обоих типов, определить скорость частицы и ее существенную опознавательную характеристику; отношение заряда к массе, e/m.
Поля и пучки
Электрическое поле к электронам мы уже прикладывали. В трубке осциллографа напряжение в электронной пушке создает поле, направленное вдоль пучка электронов, чтобы разогнать их, а отклоняющие поля качают пучок вверх-вниз и из стороны в сторону. В разрядной трубке электрическое поле, направленное вдоль нее, ведет положительные ионы в одну сторону, а электроны и отрицательные ионы — в противоположную, создавая толчею возбужденных атомов, которые испускают свет, когда их электроны возвращаются в состояния с наименьшей энергией.
Фиг. 3. Пучок частиц несет отрицательный заряд.
Пучок из электронной пушки
Пучок частиц, испускаемых горячим катодом и ускоряемых напряжением электронной пушки, несет отрицательный заряд. В этом можно убедиться, включив последовательно с вакуумным диодом миллиамперметр или поймав пучок в маленькую металлическую чашечку, соединенную с электроскопом. Чтобы показать, что все «снаряды» в этом пучке одинаковы и что они суть электроны, мы должны провести измерения, используя отклоняющие поля. В задачах к настоящей главе предлагаются данные, типичные для реальных экспериментов. Чтобы понять, как можно исследовать электроны, решите эти задачи.
Задача 3. Прямое измерение скорости электрона
В задаче демонстрируется метод, который был использован для измерения скорости электронов в пучке, вылетающем из электронной пушки. Мы применяем колебательный контур для создания отклоняющего электрического поля, действующего на пучок[103]. Имея такой контур, можно попеременно подавать на пару металлических пластин положительные и отрицательные заряды с частотой, скажем, 10 000 000 раз в секунду. Тогда и электрическое поле в пространстве между пластинами будет менять свое направление — вверх, вниз, снова вверх, снова вниз, с той же частотой: тоже 10 000 000 раз каждую секунду.
Располагая современными насосами, легко получить в длинной трубке такой хороший вакуум, что электрон проделает весь свой путь без столкновений. На фиг. 4 показана такая трубка с электронной пушкой у одного конца. Поток электронов, испущенных раскаленным катодом С и ускоренных напряжением пушки (которое составляет, скажем, 1600 в в промежутке между точками С и М), выходит через небольшое отверстие А в диафрагме пушки М и продолжает лететь вдоль трубки, больше не меняя скорости. Пара горизонтальных пластин Р1 и Р2 помещается за отверстием А, так что пучок электронов проходит через вертикально направленное электрическое поле между пластинами. Как раз за пластинами расположена перегородка с отверстием В. Если переменное электрическое поле, описанное выше, приложено к области между Р1 и Р2, оно будет раскачивать электронный пучок вверх и вниз, так что электроны будут проникать через отверстие В маленькими порциями, один раз по пути вверх, другой раз по пути вниз (ДВАЖДЫ ЗА ЦИКЛ), как струя из пожарного шланга, если ею водить по забору с дыркой. Эти порции будут лететь вдоль трубки с постоянной скоростью и. На этом пути они пролетают между другой парой пластин Р3 и Р4, к которым прикладывается то же самое переменное электрическое поле, синхронное с полем между пластинами Р1 и Р2. Вслед за этой парой пластин стоит вторая диафрагма с отверстием D. За этим отверстием расположен коллектор Е, собирающий электроны и соединенный с усилителем и счетчиком, который регистрирует электронные сгустки, достигающие Е. Отверстия А, В и D располагаются на одной прямой между С и Е.
Фиг. 4. К задаче 3. Измерение скорости электронов.
ДАННЫЕ. Отверстия В и D расположены на расстоянии 1,20 м друг от друга. Из независимых измерений известно, что колебательный контур, соединенный с обеими парами пластин, имеет частоту 10 000 000 колебаний в секунду. Если напряжение между катодом электронной пушки С и ее диафрагмой равно 1600 в, то, как это обнаружено в эксперименте, действительно имевшем место, через отверстие D на коллектор попадает много электронов. Если напряжение пушки составляет 1500 или 1700 в, то электронов мало. Заметьте, что путь, проходимый электронами в отклоняющем поле пластин, очень короток, так что электроны пролетают через поле быстро — за малую долю периода колебательного контура.
а) Укажите причину, по которой электроны не долетают до Е, если только пушка не заставляет их двигаться со строго определенной скоростью (т. е. со скоростью, соответствующей напряжению 1600 в, а не 1500 или 1700 в).
б) Оцените на основании вышеприведенных данных скорость электронов. (Сделайте простейшие предположения из всех возможных. Они приведут к тому, что ваша оценка даст максимальную скорость.)
в) Объясните, почему и некоторые другие скорости могут согласоваться с описанными наблюдаемыми фактами.
г) Рассчитайте одну или несколько таких скоростей.
д) Как бы вы попробовали выяснить (перестраивая аппаратуру), какой выбор решения, б) или г), правилен? (Эта задача требует как здравого смысла, так и тщательных размышлений.)
Фиг. 5. Напряжение, подаваемое генератором, описанным в условии задачи 3.
Задача 4. Как оценить отношение заряда к массе по напряжению на электронной пушке и скорости электрона
Поток электронов выбрасывается из электронной пушки, расположенной в конце длинной трубки. Пусть скорость их измерена (см. предыдущую задачу) и равна v. Батарея дает напряжение V между точками С и М, которое разгоняет электроны от первоначального состояния покоя до конечной скорости и, с которой они и вылетают из пушки. Каждый электрон, несущий заряд в е кулонов, проходит разность потенциалов V в, приложенную к пушке, набирая кинетическую энергию. Если вакуум хороший, то вся энергия, которую батарея передает электрону с помощью электрического поля пушки, переходит в его кинетическую энергию. Эксперименты показывают, что: если напряжение, приложенное к пушке, составляет 100 в, то электроны вылетают со скоростью и, которая в результате измерения оказалась равной 6 000 000 м/сек
(ЭТО НЕ ОПЕЧАТКА).
Используйте эти данные для оценки массы одного электрона по следующему рецепту:
а) Обозначьте массу электрона в кг через т. Запишите кинетическую энергию, с которой он движется вдоль трубки, выразив ее через m. (Запишите и единицы измерения.)
б) Обозначьте заряд в кулонах через е. Какую энергию он приобрел, пройдя через 100-вольтовую разность потенциалов электронной пушки? Выразите ее через е. (Опять не забудьте про единицы.)
в) Проследите, чтобы ответы на пункты а) и б) были выражены в одних и тех же единицах. Запишите уравнение, отражающее тот факт, что энергия, переданная электрону 100-вольтовой батареей, как раз и есть его кинетическая энергия. Решите его и найдите отношение заряда к массе для электрона, т. е. е/m.
г) В другом, совершенно особом опыте Милликен обнаружил, что заряд электрона е равен —1,6∙10-19 кулон. Если так, то чему равно значение массы электрона в кг?
Все электроны одинаковы
Прямое измерение и неудобно, за исключением случая достаточно медленных электронов; но кто бы ни делал измерения, описанные в задачах 3 и 4, из сопоставления их результатов всегда получалось одно и то же значение е/m, какую бы скорость электронов ни брали, какое бы напряжение ни прикладывали к электронной пушке. Из какого материала ни сделай пушку, значение е/m все равно получается одним и тем же: все электроны имеют одинаковое отношение заряда к массе. Этот вывод о том, что электроны едины, универсальны, был получен в результате исследований, выполненных в начале нашего столетия. Однородных пучков, создаваемых пушками с известным напряжением, тогда не было, и приходилось выполнять более сложные измерения, используя электрическое поле, чтобы отклонять электроны, а затем еще магнитное поле. С тех пор отклонения пучков в разных направлениях электрическими и магнитными полями постоянно используются в фундаментальных экспериментах атомной физики. В задаче 5 показано, как можно использовать поперечное электрическое поле.
Можно сопоставить отношение е/m с результатами других опытов, чтобы получить очень важную информацию об атомах; но и сами по себе измерения е/m позволяют высказать два утверждения огромного значения:
1) Отношение е/m имеет одну и ту же величину для всех электронов, от самых медленных до довольно быстрых, из какого бы источника они ни вылетали. Их можно испарять из раскаленной нити, выбивать из атомов металла светом (как в фотоэлементе), срывать с атомов рентгеновскими лучами, радиоактивные атомы могут выстреливать их в виде бета-частиц — результат будет тот же самый, что и при первоначальном способе выбивания их из атомов при соударениях в разрядной трубке. Это означает, что электроны все одинаковы, что электрон — универсальная составная часть материи.
2) Если производить опыты с очень быстрыми электронами, величина е/m оказывается меньше стандартной. Это означает, что если заряд е остается постоянным, то масса при высоких скоростях становится больше — в полном согласии с теорией относительности.
Задача 5. Отклонение пучка электронов электрическим полем
Одним из первых экспериментальных способов исследования катодных лучей была посылка пучка через электрическое поле (см. выше вводную задачу 2). Отношение заряда к массе для частиц в пучке можно определить также, измеряя вместо напряжения на трубке отклонение пучка».
Задача покажет вам, как рассчитать е/m по результатам таких измерений. Предположим, что пучок электронов вылетает из пушки со скоростью 2,4∙107 м/сек, т. е. 24 000 000 м в секунду (как определить эту скорость, сказано в задаче 3). Этот пучок пропускается через протяженную область, поперек которой приложено электрическое поле (фиг. 6). В конце своего пути пучок попадает на флуоресцирующий экран, так и не успев выйти за пределы области, пронизанной полем.
Фиг. 6.
Приводимые ниже данные вполне могут быть получены в реальном опыте. Представьте себе, что так оно и есть, что попытка измерить отношение е/m для электрона предпринята, и рассчитайте е/m (в кулонах на килограмм).
Скорость частиц в пучке (см. задачу 3)… 2,4∙107 м/сек.
Отклонение пучка в приложенном поле… 0,015 м вниз по вертикали.
Расстояние между пластинами, создающими поле… 0,050 м.
Длина области, в которой действует… поле 0,20 м.
Разность потенциалов между пластинами… 120 в.
(Обратите внимание, что напряжение на пушке не задается, поскольку знать его не нужно.)
Рассчитайте:
а) Напряженность электрического поля между пластинами, т. е. силу, в ньютонах, действующую на один кулон.
б) Силу, действующую со стороны поля на заряд е, т. е. на один электрон.
в) Ускорение электрона. Обозначьте его массу в килограммах через m.
г) Время, которое потребуется электрону, чтобы пересечь область 0,20 м, где имеется поле. (Примечание, 0,20 м — длина области по горизонтали, и скорость, названная выше, — тоже горизонтальная. Влияет ли как-нибудь вертикальная скорость, приобретаемая электронами? Относительно независимости движений проконсультируйтесь у Галилея.)
д) Затем рассчитайте расстояние s, которое электрон проходит по вертикали под действием поля. Для этого заметьте, что электрон попадает в поле с нулевой скоростью по вертикали и движется с ускорением, рассчитанным в пункте в), в течение времени, рассчитанного в пункте г). (В результате должна получиться формула для s, в которую войдут величины 0,20 м, заряд е, масса m и т. д.)
е) Отношение е/m. Как сказано выше, результаты измерения дают расстояние, равное 0,015 м. Напишите уравнение, показывающее, что отклонение, рассчитанное в пункте д), в самом деле 0,015 м. Решите это уравнение для е/m.
В этой задаче вам заранее была известна скорость, которая могла быть измерена методом приложения переменного электрического поля, изложенным в задаче 3. Пока вы ее не знаете, она входит в тот набор неизвестных, которые в виде комбинации e/mv2 можно рассчитать по отклонению в электрическом поле. В большинстве опытов с катодными лучами скорость неизвестна, пока не выполнены измерения с отклоняющим магнитным полем.
Задача 6. Сравнение атомов с электронами
Разговор сейчас пойдет об ионах, которые позволяют растворам проводить электрический ток. Химические данные давно указывали на то, что переносчики электричества — это отдельные атомы, а иногда группы атомов, несущих заряды, причем заряды одинаковые. Каждый равнялся крошечной универсальной «атомной единице» электричества (которая была названа «электроном» задолго до того, как были открыты настоящие электроны). В некоторых случаях заряды равнялись 2 или 3 таким единицам, В начале нынешнего столетия при изучении диффузии ионов были получены опытные данные, указывающие на то, что основная единица заряда ионов химических соединений по величине совпадает с зарядом, который несут летящие электроны и который был измерен Дж. Дж. Томсоном. Итак, определяя отношение заряда к массе У продуктов электролиза, мы выполняем измерения, которые, вероятно, с сохранением тех же самых пропорций можно было бы выполнить и над отдельными атомами. Сравнивая это отношение заряда к массе с тем, которое получено для электронов в пучке электронной пушки, мы можем, следовательно, сравнить атомы с электронами. Таким образом, для ионов содержит важную для атомной физики информацию. А как измерить это отношение, покажут приведенные ниже вопросы.
ДАННЫЕ. Когда ток проходит через воду, содержащую кислоту, с металлических пластин (электродов), по которым приходит и уходит ток, срываются пузырьки кислорода и водорода (кислота в этом случае лишь посредник, поставляющий ионы).
Опыт показывает, что при пропускании тока в 10 а в течение 1000 сек выделится 0,001244 кубометра газообразного водорода (при комнатной температуре и давлении в 1 атм).
Если в одной и той же теплой комнате взвешивать большой стеклянный шар, наполнив его сначала водородом при атмосферном давлении, затем пустой, затем наполнив водой, то весы дадут следующие показания:
Масса шара, наполненного водородом… 1,60084 кг
Масса пустого шара… 1,60000 кг
Масса шара, наполненного водой… около 11,60 кг
а) Используя эти данные, рассчитайте плотность водорода в кг/м3.
б) Чему равна масса водорода, выделившегося при «электролизе» в опыте, описанном выше?
в) Чему равен электрический заряд (= количеству электричества), прошедший через аппарат?
г) Весь заряд, притекающий на пластину, где выделяются пузырьки водорода, переносится, скорее всего, этим самым водородом. Если это так, то чему равно отношение заряд/масса для полного заряда, перенесенного полной массой водорода?
д) Предположим, что все «водородные носители» совершенно одинаковы и являются не чем иным, как атомами водорода. Чему равно е/М, отношение заряда к массе, для иона атома водорода?
е) опыты с электронными пучками показывают, что для электрона е/m составляет около 1,8∙1011 кулон/кг. (Это означает, что 1 кг электронов имел бы заряд в 180 000 000 000 кулон.) Сравните значения е/М для иона водородного атома и е/m для электрона, вычислив отношение этих значений.
ж) Полагая, что е в обоих случаях одинаково, сравните m и М.
Значения е/m
Измеряя отклонение в электрическом поле, можно вычислить отношение e/mv2. Напряжение на электродах пушки также дает нам e/mv2. Так что, если мы знаем это напряжение, то отклонение пучка в электрическом поле не дает нам никакой новой информации[104]. Чтобы вычислить отношение e/m — важнейшую характеристику заряженных атомных частиц, мы должны либо непосредственно определить v, либо измерить отклонение частиц в магнитном поле (см. гл. 37), которое даст отношение e/mv. Пока предположим, что мы можем исключить и и найти значение e/m.
Сто лет назад электроны как таковые не были известны. Единственным указанием на существование «атомов электричества» были данные электролиза, веско свидетельствовавшие в пользу того, что каждый атомный ион несет стандартный электрический заряд, имеющий одну величину для всех ионов химических соединений, за исключением лишь отдельных случаев, когда эта величина удваивалась или утраивалась. Пятьдесят лет назад были получены электронные пучки, с которыми производились самые разнообразные опыты. Дж. Дж. Томсон выполнил первые последовательные, хотя и грубые измерения зарядов и масс электронов и положительных ионов; их-то он и считал основными компонентами атомной структуры. Некоторые результаты измерений e/m и е/М приведены в таблице на стр. 274.
Если не считать изменений, происходящих при очень высоких энергиях, все электроны имеют одно и то же отношение e/m, 1,76∙1011 кулон/кг. Сравните это с отношением е/М для самого легкого из ионов, Н+. Такие ионы переносят 96 500 000 кулон на каждые 1,008 кг водорода, выделяющегося при электролизе. Так что для Н+ е/М = 9,57∙107 кулон/кг. Для электронов отношение e/m почти в две тысячи раз больше. Тогда, если е одинаково у обеих частиц, значение m у электронов должно быть почти в две тысячи раз меньше. [Несколько раньше с помощью изобретательно поставленных опытов и логических рассуждений было показано, что произведение N∙e одинаково для ионов в газах и ионов, образующихся при электролизе (N — число Авогадро). Ни N, ни е не были известны, а произведение N∙e оказалось возможным оценить: с одной стороны, существовали измерения «валового выхода» при электролизе, тех самых 95 700 000 кулон, переносимых килограммом водородных ионов, с другой стороны, хитроумные опыты с ионами газов с использованием явления диффузии. После их выполнения рассудили, что в случае ионов газов е — это заряд выбитого электрона, а N — одно и то же как для ионов, так и для электронов; следовательно, и е одно и то же.] Так впервые было показано, что электроны — это крошечные осколки атомов[105].
Таблица значений e/m и е/М
(Самые первые измерения были недостаточно точны. В таблице приведены данные, полученные уже тогда, когда были разработаны хорошие экспериментальные методики; численные результаты обычно рассчитывались по отклонениям частиц в электрическом и магнитном полях.)
Частицы ∙ Значение e/M и е/m, кулон/кг
∙ Катодные лучи в разрядной трубке: электроны, выбитые из атомов газа или металлического электрода с помощью бомбардировки. [Поскольку это был самый первый метод получения электронных пучков (благодаря нему за ними и закрепилось название катодных лучей), приводятся результаты трех различных экспериментов.] ∙ 1,775∙1011; 1,761∙1011; 1,759∙1011
∙ Электроны, вылетающие из вольфрамовой спиральки, накаленной добела (как в диоде) ∙ 1,76∙1011
∙ Электроны с раскаленного докрасна оксидного катода (какие применяются в современных радиолампах) ∙ 1,78∙1011
∙ Электроны, выбитые из металла ультрафиолетовым светом («фотоэлектрический эффект», используемый в фотоэлементах) ∙ 1,756∙1011
∙ Внутриатомные электроны, вынуждаемые внешним магнитным полем к изменению своих «орбит» (эффект Зеемана) ∙ 1,761∙1011
∙ Электроны в водородных и гелиевых атомах: использован метод сравнения электронной массы с массой атома по измерениям длин волн в спектрах, трактуемых теорией Бора, которая считается верной ∙ 1,761∙1011
∙ Медленные бета-частицы, испускаемые радиоактивными атомами ∙ 1,763∙1011
∙ Бета-частицы (медленные… умеренно быстрые… быстрые), испускаемые радиоактивными атомами; получается непрерывный набор значений ∙ от 1,76∙1011 до 0,35∙1011
∙ В более поздних экспериментах, когда электроны, испускаемые горячими катодами, стали разгонять до огромных энергий на ускорителях, нижняя граница интервала получаемых значений е/m опустилась; получены величины, в тысячи раз меньшие — это изменение связывается с релятивистским увеличением массы
∙ Положительно заряженные лучи: положительные ионы в разрядных трубках. Значение е/М зависит от того, какой газ наполняет трубку:
— ион водорода Н+ ∙ 1,76∙1011/1840
— ион кислорода О+ ∙ 1,76∙1011/16∙1840
— ион кислорода О++ ∙ 1,76∙1011∙2/16∙1840
— ионы ртути Hg+, Hg++ … до Hg++++++++ ∙ 1,76∙1011 (от 1 до 8)/200∙1840
∙ Положительные ионы при электролизе:
— ион водорода Н+ ∙ 1,76∙1011/1840
— меди Си++ ∙ 1,76∙1011∙2/63,6∙1840
— ион хлора Сl– ∙ 1,76∙1011/35∙1840
∙ Альфа-частицы, испускаемые радиоактивными атомами ∙ 1,76∙1011∙2/4∙1840
∙ И многие недавно открытые частицы (например, μ-мезоны) ∙ 1,76∙1011/~200
Вычислим дроби более точно;
m/M = (e/M)/(e/m) = 9.75∙107/1.76∙1011 = 1/1840
Электрон и атом, его потерявший (т. е. оставшийся от атома положительный ион), имеют равные и противоположные по знаку заряды, поскольку вещество обычно нейтрально. Но массы их чрезвычайно сильно отличаются. Не удивительно, что электроны так подвижны в электрических полях: легко отклоняемый пучок электроны образуют в телевизионной трубке, мгновенно, как охваченная паникой толпа, срываются с места в счетчике Гейгера. При таком большом в сравнении со своей маленькой массой заряде они ускоряются в электрических полях много быстрее, чем заряженные атомы. Лишь когда электроны приобретают огромные кинетические энергии, миллиарды электронвольт, они кажутся (неподвижным наблюдателям) такими же массивными, как атомы.
Зачем нужно знать е
Если мы сможем измерить е, то, поделив эту величину на определенное ранее отношение е/m, найдем массу отдельного электрона. А массу отдельного атома с его помощью узнать еще проще, поскольку е/М для атомных ионов легко определяется из опытов по электролизу. По атомным массам можно рассчитать массу любой молекулы, а следовательно, число молекул в любом образце жидкости или газа. Кроме того, теории атомной структуры не обходятся без вычислений, для которых необходимо знать истинную величину е. Точное знание этой величины имеет чрезвычайно важное значение.
Измерение е
К 1900 г. существование электрона как атомной частицы было установлено и определено отношение elm для него, но о величине е можно было строить лишь приблизительные догадки. Экспериментальные факты по электролизу задолго до этого указывали на то, что существуют «атомы электричества», во всем подобные друг другу, причем некоторые ионы несут по одному такому атому электрического заряда, другие — по два и т. д. К 1910 г. величина е стала крайне необходимой для развития атомных теорий — теорию Бора нельзя было бы как следует проверить, не зная как следует ни е, ни е/m. Дж. Дж. Томсон и другие попытались измерить е, формируя облачка из мельчайших водяных капелек, каждая из которых образовывалась вокруг иона с зарядом е, а затем собирая эти облачка. Это дало лишь грубую оценку, и не было никакой уверенности, что все эти заряды в точности равны[106]. Тогда Р. А. Милликен[107] и поставил свой великий эксперимент, в котором использовал крошечную капельку масла, собиравшую небольшой заряд с ионов воздуха. Он снова и снова измерял полный заряд капельки и каждый раз обнаруживал, что тот в небольшое целое число раз (например, в 1, 2 или 10) больше некоторого основного заряда, который во всех случаях был одним и тем же. Поначалу он не знал ни величины этого универсального основного заряда, «электрона», ни того, сколько таких зарядов помещалось на его капельке. Он должен был проводить измерения со многими заряженными каплями, а потом устраивать арифметическую «угадайку». Задача была «похожа на случай, когда вам надо найти вес одного яйца, если даны веса большого числа бумажных кульков с яйцами, в каждом из которых находится свое, к тому же неизвестное число яиц»[108].
Задача 7
а) Пусть кульки с яйцами весят 12,16, 28, 24 унции. Попробуйте определить вес яйца и число яиц в каждом кульке.
б) Предположим, что вам дали еще один кулек, а он весит 14 унций. Как это отразится на ваших предположениях?
в) Добавили еще один кулек, весящий 12,1 унции. К какому заключению вы придете?
По существу метод, использованный Милликеном и его предшественниками, совпадает с тем, который, как рассказывалось в гл. 33, использовался для измерения заряда металлического шара. Он заключался в измерении силы, действовавшей на шар со стороны однородного электрического поля. Для измерения е несколько электронных зарядов передавалось крошечной капельке жидкости, плавающей (или, точнее, медленно падающей) в воздухе. Капелька помещалась в вертикальное электрическое поле, которое, действуя на заряд капельки, тянуло ее вверх. Единичный заряд электрона е очень мал, и видимая дождевая капля была бы для него слишком тяжела; потребовался бы миллиард или около того электронных зарядов, чтобы в реально возможном поле удержать ее на весу. Поэтому была использована очень маленькая капля из пульверизатора, настолько маленькая, что ее по-настоящему и не видно было — лишь крошечную звездочку рассеянного ею света можно было наблюдать в микроскоп. Такая миниатюрная капелька равномерно опускается в воздухе — трение о воздух компенсирует действие тяготения. Постоянную скорость этого движения вниз можно измерить и использовать для того, чтобы «взвесить капельку». Если включить вертикальное электрическое поле, оно добавит еще одну силу: действие поля на электрический заряд капельки. В первых экспериментах электрическое поле подбиралось так, чтобы не давать капельке падать, так что она парила в воздухе. Однако большей точности удалось добиться, используя более сильное поле и заставляя капельку сперва двигаться вверх, а потом позволять ей падать в отсутствие поля. Таким образом, измерения можно было повторять, «вздергивая» капельку вверх и позволяя ей падать снова и снова, играя с ней, как кот с мышью. В этом и состояло выполненное Милликеном измерение электронного заряда — великолепный образец экспериментального исследования, которое принесло ему неувядающую славу.
Чтобы понять, как Милликен проводил свои измерения, проработайте приведенную ниже задачу 8. Капелька (чаще масляная, чем водяная) обычно образовывалась со случайным зарядом, полученным за счет трения о стенки трубки пульверизатора, подобно тому, как эбонитовая палочка электризуется о мех. Путешествуя вверх и вниз, она могла случайно изменить свой заряд, встретив ион в окружающем воздухе. Это изменение сразу сообщало ей новую скорость дрейфа вверх в электрическом поле. Иногда Милликен вызывал быстрое изменение заряда, используя рентгеновские лучи для того, чтобы выбить электроны из самой капельки. Он заставлял одну и ту же капельку многократно менять свой заряд, а после этого должен был решать задачу о «яйцах в кульке».
Задача 8. Опыт Милликена по определению заряда электрона
Милликен проводил свой опыт с маленькой масляной каплей, которая получила небольшой заряд от ионов воздуха. Он мог часами экспериментировать с одной и той же каплей, заставляя ее снова и снова подниматься вверх, а затем позволяя ей падать. В отсутствие электрического поля капля падает с постоянной скоростью, характерной для капли данного размера.
а) Проводя опыты с масляной капелькой, Милликен обнаружил, что скорость ее падения оставалась постоянной в течение многих часов, сколько бы раз ей ни позволяли падать. Однако с капелькой воды вело обстояло иначе — время ее падения постепенно увеличивалось. К какому выводу вы приходите относительно масляной капельки?
б) Во включенном электрическом поле капелька двигалась вверх с постоянной (но в разных опытах различной) скоростью. Эта скорость оставалась постоянной на протяжении многих циклов подъема, а затем вдруг принимала новое значение. Эти внезапные изменения учащались после того, как Милликен включал находившуюся поблизости рентгеновскую трубку. Дайте объяснение этих внезапных изменений.
Вот некоторые данные измерений, выполненных с одной капелькой, которая многократно падала со скоростью v = 2,305 см/мин (см. сноску на стр. 280). После включения электрического поля она в течение нескольких циклов поднималась со скоростью u1 = 2,516 см/мин. Затем скорость подъема внезапно изменилась и в течение одного или нескольких циклов была равна u2 =1,434 см/мин, затем опять изменилась до u3 = 0,903 см/мин, затем до 0,369 см/мин, потом опять до 0,903 см/мин и после принимала значения 1,958, 0,903 и 1,434 см/мин.
Как теория, так и эксперимент показывают, что при очень медленном движении шарика через вязкую жидкость (а также и при движении через воздух, если капелька достаточно мала) сила сопротивления, возникающая за счет трения о жидкость, дается выражением
F = K∙(скорость),
где К — постоянная, зависящая от коэффициента трения жидкости и радиуса шарика, а они не меняются в течение всего эксперимента с капелькой.
Когда капля падает в отсутствие поля, на нее действуют лишь две силы: ее вес m = 9,8 ньютон и сила трения K∙v. Разогнавшись вначале, капля падает затем равномерно, без ускорения.
в) Напишите уравнение, показывающее, как эти две силы связаны между собой при равномерном падении. [При написании этого уравнения используйте экспериментальное значение v = 2,305 см/мин[109].]
г) Предположим, что электрическое поле, когда оно включено, имеет напряженность X ньютон/кулон и действует на заряд капельки, равный Q кулон. С какой силой поле действует на капельку?
д) Когда поле включено, капелька движется вверх со скоростью и (например, 2,516 см/мин), и на нее действует сила трения K∙v, направленная вниз и препятствующая этому движению. Вес капли m = 9,8 ньютон — это тоже сила, направленная вниз. Начав движение, капля движется с постоянной скоростью без ускорения. Напишите уравнение, связывающее три силы, действующие на капельку.
е) Исключите из последнего выражения вес m = 9,8 ньютон, подставив его значение из первого уравнения, и перепишите результат в форме Q =… Это новое уравнение должно показывать, что Q прямо пропорционально (v + u), если X постоянно.
ж) Используйте результат, полученный в пункте е), для анализа данных измерений Милликена, которые приведены выше. Величина v равнялась 2,305 см/мин и не менялась, а разные значения и приведены выше. Если (v + u) служит мерой полного заряда Q, то изменения (v + u) должны служить мерой изменения заряда, т. е. заряда, получаемого каплей от ионов и т. д.
Изменение заряда ΔQ определяется по изменению (v + u), которое равняется изменению v+ изменение u. Но u не меняется, так что изменение v равно нулю и ΔQ определяется изменением u.
Рассчитайте изменения скорости подъема капли и используйте их для определения изменения заряда, т. е. для определения заряда, подхваченного каплей. Рассчитайте все значения изменения u. Найдите одно элементарное изменение, которое объяснит все наблюдаемые изменения, и предположите, что оно соответствует одному электронному заряду. Затем скажите, сколько электронов должно было участвовать в каждом наблюдаемом изменении заряда.
[Результаты Милликена не могли быть «абсолютно точны». Последний знак в приводимых им значениях, скорее всего, сомнителен. Так что вы не должны обращать внимания на небольшие различия. Что значит «небольшие» — ваше дело догадаться. Милликен обсуждал этот вопрос, когда разбирал возможные ошибки своего эксперимента, и даже поссорился (вспомним яйца в кульке) с одним из своих соперников, который долго отстаивал существование «субэлектрона». Сомнения в последнем знаке, который приводит Милликен, означают, что случайная ошибка может приводить к изменениям Δu в 1 или 2 %.]
з) Используя то изменение и, которое, согласно вашему решению, отвечает одному электронному заряду, вернитесь к значению (v + u), которое определяет ПОЛНЫЙ заряд, и рассчитайте, сколько электронных зарядов несла капля, начиная свое движение, когда скорость ее подъема u1 составляла 2,516 см/мин.
Расчеты в пунктах ж) и з) показывают, каким способом Милликен доказал, что все электроны имеют один и тот же заряд.
Фиг. 7. Опыт Милликена.
Универсальный атом электричества
Измерения с одной капелькой могли гарантировать существование основного атома электрического заряда. Но для того чтобы доказать, что основной «атом заряда» есть универсальная постоянная, Милликен должен был выполнить множество опытов с капельками различных размеров, с разными жидкостями и с различными способами ионизации. Если бы в каком-нибудь эксперименте обнаружилась нецелая доля введенного им гипотетического заряда вместо целого их числа, то он вынужден был бы выбрать меньшее значение «атома электричества» — и тогда необходимость переходить ко все меньшим и меньшим атомам разрушила бы как его надежды на успех, так и наши нынешние теории строения атомов.
Чтобы определить истинную величину заряда в кулонах, он рассчитал вес капельки по скорости ее падения и известному коэффициенту трения при обтекании воздушным потоком. Эти алгебраические выкладки довольно длинны, но не трудны; кроме того, в книге Милликена они прекрасно объяснены.
Результат: каково бы ни было происхождение заряда, из какого бы материала ни состояла капелька, полный заряд на ней всегда равнялся целому числу, умноженному на один и тот же основной электрический заряд
1,60∙10-19 кулон.
Это величина отрицательного заряда каждого электрона (или положительного заряда, который остается у атома, ионизованного в результате потери электрона, или отрицательного заряда иона, полученного добавлением электрона к атому). Это и есть универсальный атом электричества.
Задачи к главе 36
Задачи 1, 2 — вводные, в начале главы. Задачи 3–8 — в тексте.
Задача 9. Электричество в сравнении с гравитацией
а) Атом водорода, лишенный своего единственного электрона, называется водородным ионом или «протоном». Он имеет заряд +е. Пусть водородный ион и электрон помещены на расстоянии d м друг от друга. Используя данные, приведенные ниже, запишите:
1) выражение для силы их электрического притяжения,
2) выражение для силы их гравитационного притяжения.
б) Рассчитайте отношение электрической и гравитационной сил, вычисленных в пункте а).
в) Почему, производя расчеты при изучении атомных моделей, мы обычно пренебрегаем гравитацией?
ДАННЫЕ. Гравитационная постоянная G = 6,6∙10-11 ньютон» м2/кг2. Постоянная закона Кулона = 9,0∙109 ньютон∙м2/кулон2. Масса электрона = 1/1840 массы водородного иона (массу водородного иона обозначим через М). Заряд электрона е = —1,6∙10-19 кулон.
Задача 10. Электрон в электрическом и гравитационном полях
В типичном осциллографе, использующем катодные лучи, для отклонения электронного пучка к верхнему краю экрана или к одной из его боковых сторон используется электрическое поле 10 000 в/м. Сравните силу, с которой такое поле действует на электрон, с силой тяжести, действующей на тот же электрон.
Задача 11. Осциллограф
В корпусе электронного осциллографа помещаются радиолампы (диоды с анодом и подогревным катодом), которые выпрямляют поступающий переменный ток, превращая его в полупериодные или двухполупериодные «всплески» постоянного тока, а также катушки индуктивности и конденсаторы для переделки этих всплесков в постоянное напряжение. Там есть трансформатор, подающий переменный ток, подлежащий выпрямлению, и обеспечивающий низкое напряжение для подогревных спиралек. Но основной деталью является сама электроннолучевая трубка.
а) Набросайте упрощенный чертеж такой трубки в разрезе или сделайте объемный рисунок, обозначив ясно основные части.
б) Объясните, откуда берется зеленое пятнышко на экране.
в) Чтобы сделать зеленое пятнышко ярче, питание, подаваемое на трубку, можно изменить по крайней мере двумя различными способами. Попробуйте догадаться, что это за способы, и объясните, почему каждое из этих изменений дает желаемый эффект. (В современных трубках, когда поворачивается ручка увеличения яркости, ни один из этих двух наиболее очевидных способов не используется!)
г) Когда разность потенциалов с прибора, проверяемого с помощью осциллографа, подается на клеммы V и G, пятнышко смещается вверх или вниз (а если на клеммы подан переменный ток, то оно смещается попеременно вверх — вниз, вверх — вниз и т. д.). Объясните, как поданное напряжение вызывает такой эффект[110].
д) Когда мы хотим зафиксировать зависимость этого движения вверх и вниз от времени, мы заставляем пятнышко равномерно смещаться по горизонтали (затем очень быстро обратно, затем снова в первоначальном направлении и т. д.). Это смещение обеспечивается цепью, которая тоже помещается в корпусе прибора; она в основных чертах изображена на фиг. 8. Посмотрите на эту диаграмму и объясните, как работает такая система получения равномерного смещения (развертки). (Примечание. Быстрое движение в обратном направлении требует быстрого переключения с помощью радиолампы. Описывать лампу здесь нет смысла. На схеме указано ее включение параллельно конденсатору. Лампа содержит газ, в нем происходит электрический пробой, когда разность потенциалов достигает определенного значения.)
Фиг. 8. К задаче 11.
Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.
Электрон из состояния
покоя разгоняется в однородном электростатическом поле, модуль напряженности
которого 3,0 МВ/м. Определите модуль скорости электрона через 1,0 нс после
начала движения.
Решение.
В качестве физической
системы рассмотрим электрон. Если пренебречь взаимодействием электрона с
гравитационным, электрическим и магнитными полями Земли, а также предположить,
что он движется в вакууме, то разгон происходит только под действием
ускоряющего поля.
Поэтому движение электрона в инерциальной системе отсчета
можно описать вторым законом Ньютона и кинематическими законами
равноускоренного прямолинейного движения.
В качестве тела отсчета
возьмем лабораторию, ось OX направим в сторону
движения (т.е. против поля), выбрав начало координат в точке, из которой
электрон начал двигаться. Если спроецировать векторы, изображающие
соответствующие величины, на ось OX, с учетом того, что v0 = 0, получим:
ma
= eE, x = at2/2, v = at.
Откуда искомая скорость
v = eEt/m.
Подставив числовые
значения заряда и массы электрона, а также значения E и t, получим v = 5,3•108 м/с,
что больше скорости света в вакууме.
Так как ни в какой
системе отсчета тело не может двигаться со скоростью превышающей скорость света
в вакууме, то полученное значение скорости не может быть ответом задачи. Причиной
ошибки явилось неявно сделанное предположение о том, что движение электрона
может быть описано законами классической механики.
Изменение импульса тела
равно импульсу силы, действующей на него, т.е. Dp = FDt, не только в
классической, но и в релятивистской механике. Причем пот релятивистских
скоростях движения импульс тела p = gmv.
С учетом этого,
применительно к ситуации, описанной в задаче, теорему об изменении импульса
можно записать в виде: D(gmv)=eEDt.
Принимаем во внимание,
что Dv = v –
v0 = v, Dt = t – t0 = t (т.е. в момент времени t0 = 0 скорость v0 = 0).
Откуда находим модуль
искомой скорости электрона v.
Ответ: v = 2,6•108 м/с.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
5
18-Jul-19
Лекция
№ 6
Движение
электрона в электрическом поле
Электронная
оптика занимается задачами
-
формирования,
-
фокусировки
-
отклонения
электронных
пучков с помощью
-
электрических
и -
магнитных
полей.
Ее
физической основой является аналогия
между
-
законами
распространения света
и -
движением
заряженных частиц,
в том числе и электронов,
в
электрических и магнитных полях.
Эта
оптико-механическая аналогия позволяет
подойти к задаче о траектории движения
электрона
-
как
c
механической, корпускулярной,
точки зрения, когда электрон рассматривается
как частица, -
так
и с оптической, волновой,
позиции, когда учитываются волновые
свойства электрона.
В
первом
случае (корпускулярный
подход)
задача нахождения траектории электрона
решается на основе использования второго
закона Ньютона:
 (1)
(1)
 ;
;
 (2)
(2)
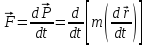 (3)
(3)
-
где

—
сила, действующая со стороны поля на
электрон; -
 —
—
скорость электрона; -
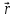 —радиус-вектор
—радиус-вектор
электрона, характеризующий его положение
в пространстве в момент времени t
относительно
некоторого начала координат..
Если
сила
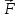
известна,
то можно, решив уравнение (3), найти
зависимость радиуса-вектора
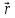
от
времени и тем самым установить траекторию
движения электрона. Однако точное
интегрирование этого уравнения возможно
лишь для случая весьма простых полей,
в частности, однородных электрических
и магнитных. В более сложных случаях
приходится прибегать к приближенным
методам решения этого уравнения.
При
волновом
подходе к задаче движения электрона
используется аналогия с принципам
Ферма в
оптике, утверждающем, что из всех
возможных траекторий между двумя точками
А
и
В
световой
луч распространяется по той, которая
имеет наименьшую оптическую длину, так
что
 (4)
(4)
где:
n
— показатель преломления;
dl.—
элемент траектории светового луча.
Как
в световой, так и в электронной оптике
из принципа Ферма следует основной
закон геометрической оптики — закон
преломления.
-
Электрическое
поле (в отличие от магнитного) вызывает
изменение величины
скорости электрона (включая
ее направление). -
Магнитное
поле приводит только к изменению
направления
скорости электрона.
Для
стационарного поля сумма потенциальной
и кинетической энергии движущегося в
этом поле электрона является величиной
постоянной

(5)
Если

то

Потенциальная
энергия электрона в электростатическом
поле в точке, характеризуемой потенциалом
φ,
равна Епот
= – eφ
Выберем
на траектории электрона две точки, из
которых одна произвольная, а вторая
лежит на катоде, эмиттирующем электроны.
У
электрона на
поверхности
катода (x=0)
энергия слагается из
-
потенциальной
-еφ0
и -
кинетической

составляющих.
У
электрона, находящегося на
расстоянии
X
от катода энергия также слагается из
потенциальной
-еφ1
и кинетической

составляющих.
Тогда
на основании формулы (2) можно написать,
что
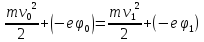 (6)
(6)
затем

(7)
Примем
во внимание, что на катоде скорость
электрона

значительно
меньше скорости
 ,
,
а потому может быть приравнена нулю,
как и потенциал φ0
на поверхности катода также равен нулю.
Тогда
 ,
,
Т.е.

φ1=
U,
и тогда
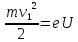
(8)
где
U
—
разность потенциалов, пройденная
электроном на траектории своего движения.
Поскольку,
проходя разность потенциалов U,
электрон
приобретает скорость V1,
т.
е. ускоряется,
величина U
носит
название ускоряющего напряжения.
Если
U<
0,
то при движении по траектории электрон
будет терять свою скорость и U
будет
являться напряжением замедляющим.
Уравнение
(3) дает возможность выражать энергию
электрона и его скорость через разность
потенциалов
U,
которую
должен пройти первоначально покоившийся
электрон, чтобы приобрести скорость V
или
соответствующую ей кинетическую энергию
 .
.
Единица
измерения кинетической энергии электрона:
1
электронвольт = 1,6•10-12
эрг = 1,6•10-19
дж
/var/www/studfiles2/data/www/download/2706/299/Qis9IxpslN.CR3t
Соседние файлы в папке Новая папка
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Скорость – электронный пучок
Cтраница 1
Скорость электронного пучка после вылета из электронной пушки поддерживается постоянными потенциалами спирали н коллектора и зависит от потенциалов первого и второго анодов. Для обычных анодных напряжений до 1 5 – 2 кв эта скорость не превышает 0 1 скорости электромагнитной волны. При таком соотношении скоростей, когда скорость электромагнитной волны значительно больше скорости пучка электронов, взаимодействие пучка и волны оказывается весьма неэффективным. Для получения эф-фектившюго взаимодействия необходимо снизить скорость электромагнитной волны, что и достигается применением замедляющего элемента.
[1]
С изменением ускоряющего напряжения меняется скорость электронного пучка и соотношение (11.7) становится верным для другой волны, которая и будет генерироваться.
[2]
Зависимость коэффициента усиления G от скорости VQ электронного пучка ( рис. 4.4 в) имеет вид, типичный для любых ЛБВ: максимальное значение величины G достигается при VQ близкой к фазовой скорости УФ медленной волны в плазме, но при VQ немного больше Уф, при появлении значительного рассинхронизма, коэффициент усиления падает. При токах пучка 10 мА была обнаружена вторая область усиления, для которой VQ значительно превосходит синхронную.
[3]
Частота генерируемых колебаний зависит от величины ускоряющего напряжения, при изменении которого меняются скорость электронного пучка и условия согласования, и усиления будут наблюдаться для другой обратной гармоники.
[4]
При изменении ускоряющего напряжения частота генерируемых колебаний будет меняться, так как изменяется скорость электронного пучка и условия самовозбуждения в лампе будут уже выполняться для другой частоты, на которой шумовая обратная пространственная гармоника будет иметь фазовую скорость, немного меньшую, чем скорость электронов.
[5]
Заметим, что в схемах с распределенными резонаторами эффективность взаимодействия в отличие от схем с обычными резонаторами существенно зависит от отношения фазовой скорости прямой волны системы к скорости электронного пучка.
[6]
Если фазовая скорость волны будет близка к скорости электронного пучка ( этого можно добиться путем замедления волны в той или иной искусственной среде – замедляющей системе), то при определенных условиях получим усиление электромагнитной волны в такой системе. Осознание этого позволило в свое время создать Рудольфу Компфнеру, чьи слова приведены в эпиграфе к предисловию к курсу лекций, электронные приборы с длительным взаимодействием, наиболее известный из которых – лампа бегущей волны.
[7]
Поток электронов может быть легко сфокусирован с помощью кольцевого электромагнита и направлен на анод, в качестве которого используется нагреваемый материал. При наложении высокого напряжения между анодом и катодом скорость электронного пучка резко возрастает, и при столкновении его с анодом кинетическая энергия превращается в тепло, обеспечивая очень высокую ( 4000 К и выше) температуру. Расплавляемый материал стекает в водоохлажденный кристаллизатор, где застывает и охлаждается.
[8]
Вторым условием справедливости законов геометрической оптики является возможность пренебрежения взаимным отталкиванием электронов в пучке. Строго говоря, это выполняется лишь в том случае, если скорость электронного пучка равна скорости света.
[9]
Неустойчивость Бунемана связана с раскачкой колебаний ионов за счет взаимодействия ионов с пучком электронов. При этом мы считаем, что разброс электронов по скоростям мал по сравнению со скоростью электронного пучка.
[10]
При прохождении электронов вдоль оси спирали, когда по ней распространяется электромагнитная волна, происходит группирование электронов в сгустке. В начале спирали электроны пучка равномерно распределены вдоль оси; затем скорость электронов, попавших под действие отрицательной ( тормозящей) полуволны продольного поля, снижается, а скорость электронов, попавших в положительную ( ускоряющую) полуволну продольного поля, увеличивается, вследствие этого плотность электронного пучка сделается неравномерной и появятся сгустки электронов. Когда скорости электронного пучка и волны равны ( уэ1ф), то электроны по всей спирали будут взаимодействовать с теми полуволнами продольного поля волны, в которые они попали при входе в поле.
[11]
В окрестности частоты отсечки сопротивление связи остается конечным, но очень большим, что эквивалентно в линейной теории большим коэффициентам усиления, которые не подтверждаются физическим экспериментом. Дело в том [9], что по мере приближения к частоте отсечки одноволновое приближение становится не корректным, так как синхронным с пучком становится не только прямая гармоника, но и обратная. Прямые линии соответствуют электронному пучку и отражают тот факт, что скорость электронного пучка не зависит от частоты. На рисунке выбраны значения скорости, соответствующие синхронизму на границах полосы прозрачности для 1 – й гармоники попутной волны.
[12]
Другим типом полупроводниковых ОКГ являются лазеры с электронным возбуждением. Используются полупроводниковые пластины толщиной 0 2 мм со сколотыми гранями, образующими резонатор. Когерентное излучение выходит из резонатора через грани в направлении, перпендикулярном направлению скорости электронного пучка.
[13]
Яркость пятна на экране электронно-лучевой трубки при определенном материале покрытия экрана зависит от числа ударяющихся об экран электронов в единицу времени и от их скорости. С другой стороны, чувствительность к отклонению обратно пропорциональна аксиальной скорости электронов. При значительном отклонении луча на экране требуется большая скорость электронов в пучке, чтобы создать достаточную яркость траектории движения луча на экране, необходимую для визуального наблюдения. Однако увеличение скорости электронного пучка снижает чувствительность к отклонению. Эту трудность можно частично обойти, если применить ускорение электронного луча после отклонения. В трубках этого типа потенциал второго анода достаточно низкий, чтобы получить удовлетворительную чувствительность к отклонению. Дополнительный электрод, увеличивающий яркость, располагается вблизи экрана на внутренней части трубки и имеет форму кольца. Потенциал этого электрода примерно в 2 3 раза больше, чем потенциал второго анода. Таким образом, скорость электронов и, следовательно, яркость пятна на экране значительно увеличиваются без снижения чувствительности трубки к отклонению. Еще большие скорости электронов можно получить, если ввести в трубку несколько дополнительных ускоряющих электродов, чтобы постепенно довести ускоряющее напряжение до величины, превышающей напряжение второго анода примерно в 10 раз. Таким путем сводятся к минимуму искажения при отклонении, возникающие благодаря существованию полей между электродами, увеличивающими яркость, вторым анодом и отклоняющими пластинами.
[15]
Страницы:
1
