Эта статья отвечает на вопрос «как найти постоянную скорость с учетом трения?» Сначала мы обсудим движение с постоянной скоростью без трения, а затем перейдем к обсуждению движения с постоянной скоростью с трением.
Когда мы говорим, что скорость постоянна, подразумевается, что ускорение частицы равно нулю. Объект движется с нулевым ускорением с той же величиной скорости (величина скорости и скорость одинаковы). В этой статье обсуждается постоянная скорость с трением.
Что такое скорость?
Термин скорость указывает на скорость и направление движения объекта. Оба в комбинированной форме называются скоростью. Мы рассмотрим математическое представление скорости в следующем разделе.
Скорость также можно определить как скорость, с которой смещение движущегося объекта изменяется со временем. Математически скорость можно представить как dx/dt. Где x — смещение, t — период времени.

Изображение кредита: Википедия
Когда говорят, что скорость постоянна?
Можно сказать, что скорость постоянна, когда говорят, что значение ускорения равно нулю (неравномерно или постоянно). Давайте изучим больше о движении с постоянной скоростью.
У всех нас есть представление о том, как работает упаковочная промышленность. У них есть конвейерная система, на которой размещаются их продукты. Конвейер движется с постоянной скоростью, чтобы рабочие и другие автоматизированные машины могли выполнять свои обязанности с продуктом. В этой статье мы увидим больше таких примеров.
Как найти постоянную скорость с учетом трения?
Если объект толкнуть, он будет двигаться вперед на некоторое расстояние, а затем остановится из-за действия сила трения.
Чтобы объект продолжал двигаться, нам нужно продолжать прикладывать силу, равную величине кинетического трения. Это тип трения, который действует между двумя движущимися поверхностями. Мы узнаем больше о кинетическом трении в следующих разделах этой статьи.
Виды трения
Существуют в основном два типа трения. Они есть-
Статическое трение
Трение покоя — это минимальная сила, необходимая для перемещения объекта из его исходного положения. Любой усилие меньше статического трение не сможет сдвинуть предмет.
Кинетическое трение
Кинетическое трение возникает, когда два объекта трутся друг о друга. Если сила, которая приводит в движение объект, поднимается, кинетическое трение должно нести ответственность за прекращение движения объекта.
Следовательно, мы можем сказать, что статическое трение — это минимальная сила, необходимая для перемещения объекта, а кинетическое трение — это минимальная сила, необходимая для поддержания движения объекта.
Пример постоянной скорости
Мы можем идентифицировать бесчисленное количество объектов, которые следуют движению с постоянной скоростью. Давайте посмотрим некоторые из примеры движения с постоянной скоростью ниже-
- Революция Земли- Наиболее распространенным примером постоянной скорости может быть Земля вращающийся вокруг Солнца. Одно и то же время требуется для совершения одного оборота, именно это и называется постоянным угловая скорость движение. Термин угловой определяет тип движения, совершаемого Землей.
- Предельная скорость- При свободном падении объект сначала ускоряется за счет действия силы тяжести. Позже ускорение становится равным нулю, как только объект достигает предельная скорость, силы сопротивления также постоянны подразумевая, что они не будут больше замедлять объект. Это пример движения с постоянной скоростью.
- Конвейерная система- Как обсуждалось выше, конвейерные ленты будут двигаться с постоянной скоростью для транспортировки продуктов из одного места в другое.
- Самолеты во время полета- В крейсерском режиме самолет стремится сохранить свою скорость. Любое изменение скорости незначительно. Это можно рассматривать как пример постоянной скорости движение.
- Вращение Земли- И снова пример постоянная угловая скорость движение. Земле потребуется двадцать четыре часа каждый день, чтобы совершить один оборот вокруг своей оси.
- Толкание коробки с той же силой– Когда мы толкаем коробку с одинаковой силой, коробка продолжает двигаться до тех пор, пока сила не будет снята. Ящик будет двигаться с постоянной скоростью, но только до тех пор, пока к нему не будет приложена та же сила.
- Вентилятор– Когда мы держим вентилятор включенным на той же скорости, вентилятор следует движению с постоянной угловой скоростью.
Что такое трение?
Он определяется как противодействующая сила или сила сопротивления движущемуся объекту. В идеальных случаях мы пренебрегаем трением, чтобы облегчить наши расчеты.
Трение отсутствует, когда поверхности гладкие, но в действительности ни одна поверхность не является идеально гладкой. Поверхность всегда имеет некоторую шероховатость. Когда объект трется о другой объект, шероховатые поверхности совпадают друг с другом, создавая сопротивление движению. Это сопротивление называется трением.
Применение трения
Хотя трения могут показаться нам нежелательными. Но он несет в себе множество применений для нас. Без трения наша жизнь превратилась бы в беспорядок.
Да, вы правильно прочитали. Трение — это то, что нам нужно, чтобы с легкостью выполнять наши повседневные задачи. Давайте получим более четкое представление о том, как трение помогает нам в наших повседневных задачах. Применение трения:
- Прогулки– Сила трения между землей и ногами помогает нам двигаться вперед. Без действия трения наши ноги соскользнули бы, и нам было бы трудно двигаться вперед.
- ВЕЛО МАСКИ– Шины велосипеда трутся о землю, благодаря чему он получает нормальную реакцию в прямом направлении. Эта нормальная реакция помогает циклу двигаться вперед.
- Вождение автомобиля- Только в вождении мы можем увидеть множество применений трения. При вращении руля необходимо трение, а при вождении возникает трение между шинами и землей.
- Альпинизм – рассмотрим поверхность без трения. Если бы мы собирались подняться по этой поверхности, то наши ноги соскользнули бы из-за гладкой поверхности. Скольжение во время подъема очень фатально. Следовательно, чтобы создать трение, мы носим обувь с лучшим сцеплением, которое создает больше трения, что помогает нам в лазании.
- Применение тормозов- Тормоза работают по принципу трения. Без трения было бы почти невозможно остановить транспортное средство. Только с помощью трения работают тормоза и помогают автомобилю остановиться, когда это необходимо.
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение тела, возникающее вследствие силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ – тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Под действием сила трения $overline{F}_{mp} $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.
Рисунок 1.
Так как сила трения $overline{F}_{mp} $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $left|overline{F}_{mp} right|$, то:
Но ускорение определяется также формулой:
где $v_{0} $- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
«Движение тела под действием силы трения» 👇
Таким образом:
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Так как $v=0$, то:
Так как $overline{a}=-frac{left|overline{F}_{mp} right|}{m} $, получим:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
Пример 1
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $mu =0,25$.
Найти: $v$-?
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
$l=frac{mv_{0}^{2} }{2overline{left|F_{mp} right|}} $. (1)
Так как $F_{mp} =mu mg$, подставим в формулу (1) и получим:
$l=frac{mv_{0}^{2} }{2mu mg} $. (2)
Выразив из формулы (2) $v_{0} $найдем величину искомой скорости:
$v_{0} =sqrt{2mu gl} =20$м/с
Ответ: Скорость автомобиля до выключения двигателя $v_{0} =20$ м/с.
Пример 2
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_{0} =20$м/с, $t=40$с.
Найти: $F_{mp} $, $mu $-?
Решение:
Уравнение движения сноубордиста будет иметь вид:
[ma=F_{mp} .]
Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
[a=-frac{v_{0} }{t} .]
Тогда:
$F_{mp} =ma=-mfrac{v_{0} }{t} =40H$.
Так как сила трения $overline{F}_{mp} $равна $F_{mp} =mu Bg$, находим коэффициент трения $mu $:
[mu =frac{F_{mp} }{mg} =0,05.]
Ответ: $F_{mp} =40H$, $mu =0,05$.
Пример 3
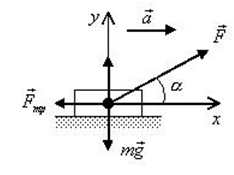
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $alpha =30^circ$, $mu =0,5$.
Найти: $a$-?
Решение:
Рисунок 2.
Уравнение движения тела:
[moverline{a}=moverline{g}+overline{N}+overline{F}+overline{F}_{mp} .]
Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
[begin{array}{l} {ma=Fcos alpha -F_{mp} } \ {0=-Bg+N+Fsin alpha } end{array}]
Поскольку $F_{mp} =mu N$, а из второго уравнения $N=mg-Fsin alpha $, то $F_{mp} =mu (mg-Fsin alpha )$. Тогда из первого уравнения ускорение:
$a=frac{1}{m} [Fcos alpha -mu (mg-Fsin alpha )]approx 7,6м/с^2$
Ответ: $a$=$7,6м/с^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
$begingroup$
If you have an object moving at $u$ initial velocity with no acceleration, and a surface with a $$mu_k$$ frictional coefficient, how can you calculate its final velocity after having traveled $d$ distance over this surface?
Would I also need mass $m$ to figure this out?
I’ve tried looking for a formula to help me out but unfortunately I was unable to find it… I’d really appreciate some help on the matter!
Qmechanic♦
187k39 gold badges486 silver badges2132 bronze badges
asked Mar 10, 2018 at 8:27
$endgroup$
7
$begingroup$
The frictional force is $mu_k mg$ opposite to $u$. We get a decelaration of $a=mu_k g$ and this finally gives us $v=sqrt{u^2-2ad}$.
Cheers!
answered Mar 10, 2018 at 8:36
$endgroup$
0
$begingroup$
Equate work done by friction force per travel distance $d$ to the loss of kinetic energy :
$$ mu_k mg,d = frac {m (u – v)^2}{2} $$
Then solve equation for $v$.
answered Aug 23, 2022 at 7:37
$endgroup$
Динамика, найти скорость, зная массу, мощность и коэф. трения
Найти скорость, зная массу, мощность и коэф. трения качения
#20882
2015-01-21 14:19 GMT
Доброго времени суток. Не смог решить подобную задачу:
Поезд массой 1000 тонн идет по горизонтальному участку пути с постоянной скоростью. Коэффициент трения качения равен 0,05. Развиваемая тепловозом мощность 5 МВт. Найти скорость поезда?
Заранее спасибо за любую помощь)
#20883
2015-01-21 15:33 GMT
Поскольку движение равномерное – сила тяги равна силе трения
(F_t=kmg)
работа есть
(A=F_tS=kmgS)
Мощность
(N=frac{A}{t}=frac{kmgS}{t}=kmgV)
откуда и находим скорость
S – пройденный путь

как найти начальную скорость если известны масса, площадь и коэффициент трения.
Дано m=200г; s=50м; коэффициент трения=0,2 найти Uo-?
Комментарии

Это не площадь, это путь :))


спасибо ,да путь, извините условия нету, нарисовали только данные сейчас ссылку на картинку кину https://pp.userapi.com/c831308/v831308483/45269/mTrX9USwe98.jpg

Очень жаль, что нет задачи, попробую по данным найти сейчач

Светило науки – 864 ответа – 7770 раз оказано помощи
Дано:
m = 0,2 кг
S = 50 м
u = 0,2
Найти: Uo – ?
Решение:
Работа силы трения равна изменению кинетической энергии:
A силы трения = Е к
F тр × S = mU²/2
F тр = umg
umgS = mU²/2
ugS = U²/2
U = √2ugS
U = √2 × 0,2 × 10 м/с² × 50 м ≈ 14 м/с