Скорость, время и ускорение
Расчеты
Три этих физических величины взаимосвязаны между собой процессом движения. Если известны две из этих величин, можно найти третью.
Скорость тела при условии равноускоренного прямолинейного движения определяем по формуле:
V = V0 + а*t
V0 — начальная скорость (при t = 0);
а — ускорение;
t — время.
Итак, чтобы найти скорость, к начальной скорости прибавляем произведение ускорения на время.
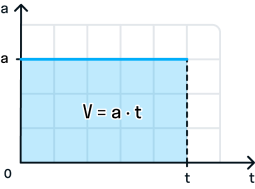
Если V0 = 0, то V = а*t.
Чтобы найти время, нужно вначале найти разность между скоростью в данный момент и начальной скоростью, затем полученный результат разделить на ускорение.
t = (V — V0) / а
Ускорение показывает изменение скорости движущегося тела, рассчитывается по двум скоростям и времени. Чтобы вычислить ускорение, следует найти разницу между скоростью в данный момент и начальной скоростью, затем все это разделить на время.
При ускорении:
а = (V — V0) / t
При торможении:
а = (V0 — V) / t
Ускорение — величина векторная, которая задается не только числом, но и направлением, измеряется в метрах в секунду (м/с2).
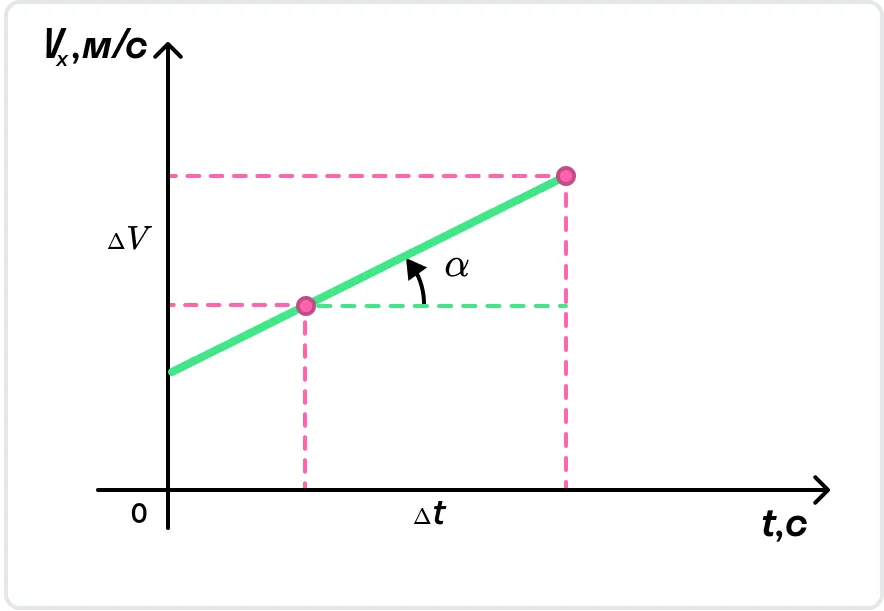
Чтобы рассчитать среднее ускорение, находим разницу между начальной и конечной скоростями Δv, полученный результат делим на разницу между временем Δt.(начальным и конечным) :
а = Δv / Δt
Быстро и правильно рассчитать величину скорости, ускорения или найти время вам поможет онлайн калькулятор.
Расчет скорости, времени и ускорения
Давно планировал начать рубрику для школьников и студентов (а может и не только для них), в которой будет рассказываться о методах решения конкретных задачи и подготовке к экзаменам по физике. Само собой, в этой же рубрике мы поговорим и про егэ по физике, которое пугает ребят больше всего. Пусть рубрика на канале называется #инженер репетитор
Ну а начнем с самого простого – научимся решать задачи на скорость. Эти задачки являются базой для дальнейшего понимания кинематики и динамики, и будут вылезать на протяжении всей механики.
Давайте сначала кратенько вспомним, а что такое скорость?
Кратко про скорость в физике
Скорость в физике – это то насколько быстро изменяется некоторая физическая величина с течением времени. Векторная величина, которая имеет размер и направление.
Например, мы нагреваем комнату. Каждый час система отопления прибавляет в комнате один градус. Значит, скорость прогрева комнаты составляет один градус в час. Или едем мы на велосипеде и за один час проезжаем 20 км. Значит, мы едем со скоростью 20 километров в час.
Вот собственно и всё, что нужно помнить из теории по этому вопросу.
Задачки на скорость обычно сконцентрированы в разделе механики, но вылезают и в других более серьезных разделах физики – скорость света, время течения какой-то реакции, скорость изменения чего-то.
Однако, разобравшись как решать подобные задачи для движения чего-то материального, разобраться и в других разделах проблем не составит. Так или иначе, когда говорят про задачи на скорость, обычно подразумевают именно кинематику и динамику.
Итак, а какие собственно задачи в этой теме бывают и как их решать :)?
Задачи по скорости и их типы
Все задачи из этой темы обычно сводятся к тому, что нужно вытащить скорость из некоторой закономерности. Для этого нужно понимать и примерно помнить формулировки, связанные со скоростью. Их не так много. Не забываем и классические косяки – например привести всё к единой системе СИ.
Самые простые задачки на скорость
Самый простой случай, когда нам известно пройденное расстояние и время, а нужно найти скорость:
S = v * t, значит V = S / t
Находим скорость в м/с или км/ч.
Задачки на “встречу”
Задачки на “встречу”. Кто-то едет навстречу кому-то или кто-то кого-то встретил. Обычно такие задачки, с помощью витиеватого условия, пытаются заморочить читателю голову, но суть-то от этого не меняется.
Нам, например, задают граничные условия и указывают, что два мотоциклиста едут по одной дороге в одну сторону и выехали одновременно. Дальше они встретились. Ну и один другого подождал на точке встречи. Один едет 20 минут, а другой едет со скоростью 50 км/ч 60 минут. Найдите скорость первого мотоциклиста. Проблем быть не должно 🙂
Считаем по приведенной выше формуле сколько проехал второй мотоциклист до времени встречи. Из этого расстояния выражаем скорость первого мотоциклиста. Ведь в точке встречи расстояние, которое они проехали было одинаковым. Вот вам и решение.
Вообще, относительно, всей этой тематики, очень полезно освоить процесс рисования чертежей и схем. Нужно сделать доходчивую и понятную схему, которая будет в нужном масштабе отражать все перемещения и их особенность. Это будет залогом практически 100% успеха. Плюс внимательность!
Задачи на скорость в присутствии ускорения
Задачки на равноускоренное движение. Этот тип задач чуть сложнее. В дело вступает ускорение. Что такое ускорение? Это уже, в свою очередь, быстрота изменения скорости. Обозначается буквой а.
Обычно большая часть величин для решения такой задачи дана или выводится из нехитрой формулы:
V = Vo + аt, где V – скорость, а – ускорение, t – время движения.
В отличие от равномерного движения тело тут перемещается равноускоренно. Т.е. за каждый интервал времени скорость изменяется на одинаковую величину. Это применимо, например, к свободному падению с высоту. Пусть всё тот же мотоциклист едет первый час со скоростью 40 км/ч, а потом разгоняется до 60 км/ч и дальше ускоряется на 20 км/ч каждый час.
Опять-таки, все задачи тут завязаны на “кручу верчу обмануть хочу”. И да, на всякий случай отмечу, что все наши рассуждения из пунктов 1 и 2 тут тоже применимы, а ещё ускорение может получиться отрицательным и это не должно вас пугать.
Для решения задач из данной категории вам потребуется внимательно читать условие задачи и включить логику.
Задачки на среднюю скорость
Задачки на среднюю скорость. Тоже очень просто решаются. Что такое средняя скорость – это скорость, полученная как среднее арифметическое от скоростей на каждом из участков.
V средняя = Весь путь (S1+S2+S3+…) / всё время (t1+t2+t3+…)
Ну а дальше опять комбинаторика :). Подставь-посчитай-вырази. Ловкость рук и внимательность.
Сразу отмечу, что когда мы обсуждаем скорость или ускорение в том разрезе, как мы его видели до сих пор, мы всегда подразумевали именно среднее значение величин. Или не совсем-таки среднее, но условно разбитое на удобное для вычисления количество участков. Усредненное если желаете. В жизни же всё немного иначе.
Речь идёт о том, что если вы представите реальное движение того же несчастного мотоциклиста (или любого другого тела), о котором мы уже много раз вспомнили, он не будет ехать равномерно. Он поедет с рваным ритмом. Там на светофоре постоял. Там перед ямой затормозил. Дальше мотобат его хлопнул, документы проверяет…Бед будет много! И всё это отражается на скорости и как следствие – на ускорении. Это значит, что он действительно может проехать за час свои 50 км, но при этом за полчаса он проедет не 25 км, как мы ожидаем, а всего лишь 10 км, а дальше нагонит разницу.
Если мы высчитываем интегральный или усредненный показатель, нам в принципе-то, фиолетово. Главное, чтобы цифры сошлись. Но если нам нужно определить значение в конкретный момент, то расчёты уже будут неточные. И тут…
задачки, где есть мгновенная скорость
Что такое мгновенная скорость?
Это скорость в конкретный момент времени. Берем мотоциклиста, смотрим на его траекторию. Тыкаем пальцем в любую точку и узнаем, что там скорость пусть 10 км/ч. А через 5 минут уже 70 км/ч. А ещё через 10 минут – опять 10 км/ч. И вовсе не 50 км/ч на всём участке. Или ещё лучше – рисуем график изменения его расстояния в зависимости от времени. По такому графику всегда можно найти мгновенную скорость.
Как подступиться к подобным задачкам?
Для начала мы вспомним, что скорость это – первая производная от функции изменения расстояния по времени. Ведь производная – это и есть скорость изменения величины.
Дальше нам нужна функция, по которой изменялось расстояние. Без неё ничего решить не выйдет. Ведь данных попросту нет.
Исходя из формы кривой у нас будет её уравнение. Дальше нужно его дифференцировать.
Также в этом разделе часто вылезает некоторое дельта R. Что это такое и почему оно в формуле? Это всего лишь то самое значение расстояния (ничтожно малое), пройденного телом, за время стремящееся к нулю.
Ну и да…Для решения задач теперь нужно учитывать, что скорость мгновенная. Больше ничего не меняется.
Задачки на скорость при движении по кривой или окружности
Ещё мы можем столкнуться с понятием угловой скорости.
Начнем с того, что определим, чем вообще ситуация при движении по окружности отличается от ситуации с движением по обычной траектории? По сути дела ничем, кроме того, что путь будет высчитываться относительно окружности – будем считать длину окружности или дуги по известным всем формулам и использовать приведенные ранее зависимости для нахождения скорости.
Это тот самый случай, про который я говорю что учить без понимания бессмысленно. Ведь по сути нам сейчас нужно запомнить только формулы, приведенные раннее, а для криволинейного движения всё высчитаем, опираясь на них и понимая суть вопроса.
Но ко всему этому добавится угловая скорость. Что это? При движении материальной точки по окружности у неё есть линейная скорость, а есть угловая. Смотрим картинку.
Линейная скорость обозначена V, а угловая W (омега). Линейная скорость – это та же скорость, что мы разобрали выше. Она же мгновенная в данном случае. Скорость материальной точки, направленна по касательной к траектории.
Угловая скорость – это то, насколько быстро вращается наш радиус R. Представьте себе часы со стрелками. Стрелка вращается с некоторой скоростью, или – изменяет угол с некоторой скоростью. Вот вам и угловая скорость 🙂 И всё! Считается вот так:
Видите, логика совершенно такая же, как мы рассматривали выше.
Соответственно, в задачках на угловую скорость нужно мыслить аналогично самому первому пункту в нашем гиде. Это просто обычная материальная точка (тело) которая перемещается по окружности. Отличается только траектория ,а в отдельную тему это выделяют попросту для удобства восприятия.
Также, если есть задачка на криволинейное движение, то нужно иметь представление о виде траектории движения тела. Если траектория сложная, то её разбивают на простые геометрические формы и суммируют результаты.
Если нужно сложить скорости
Ещё бывают случаи, когда нужно выполнять сложение скоростей. Например, сложить две скорости разных тел и найти результирующую. Или сложить скорости одного тела.
Опять-таки, бояться таких задачек не нужно!
Вся логика строится из навыка оперировать с векторами.
Скорость – это величина векторная. Значит и зарисовать её можно с помощью вектора определенной длины. Вектора скорости могут быть расположены в одной плоскости или в объеме.
Советую посмотреть вот этот ролик на моем канале
Если вектора скорости находятся в одной плоскости то всё совсем просто. Чаще всего решение сводится к операциям над прямоугольными треугольниками. Бывают и очень простые случаи – векторы скорости вообще направлены вдоль одной прямой. Уже неважно разно направлены они или сонаправлены.
Чуть сложнее ситуация, если векторы скорости расположены в объеме. Там мы приходим к единичным векторам. Ситуация более геморройная, но от того не более сложная.
———————-
Итак, друзья!
Я постарался изложить все основы, которые могут помочь вам разобраться с решением задач на скорость. Очень надеюсь, что материал вам поможет.
Писать и разбирать каждую задачку – это довольно объемная штука. Такое нужно рассматривать уже в формате индивидуальных занятий.
Если я забыл осветить что-то в статье или не полностью/непонятно раскрыл теорию вопроса – пожалуйста пишите об этом в комментариях и я дополню статью и отвечу на ваш вопрос :)…Давайте вместе сделаем полезный и полный мануал. Ещё можно спросить меня в социальных сетях прямо на страничке https://vk.com/inznan или на лицекниге https://web.facebook.com/inznan
Ну и ответьте пожалуйста на вопрос, нужны ли такие материалы на моем проекте:
Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.
Примеры равноускоренного движения:
- разгон самолета перед взлетом;
- падающая с крыши сосулька;
- торможение лыжника на горном склоне;
- разгоняющийся на склоне сноубордист;
- свободное падение в результате прыжка с парашютом;
- камень брошенный под углом к горизонту;
Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Равноускоренное движение: формулы
Формула для скорости при равноускоренном движении:
Vк=Vн+at
где: Vк — конечная скорость тела,
Vн — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.
Формула для ускорения при равноускоренном движении:
a=(Vк-Vн)/t
Во время движения тела ускорение остается постоянным.
Задача 1
Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.
Формула расстояния при равноускоренном движении
- Если известны время, скорость начальная и скорость конечная
S = t*(Vн+ Vк)/2
- Если известны время, скорость начальная и ускорение
S = Vнt + at2/2 = t*(Vн + at/2)
где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
2аS = Vк2−Vн2
где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.
Задача 2
Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.
Равноускоренное движение: графически
График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.
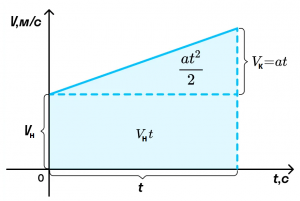
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника Vнt и треугольника at2/2. Получим: S = Vнt + at2/2.
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.
Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.
Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = Vк2−Vн2
Получим: а = (Vк2−Vн2 )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = Vнt + at2/2.
Получаем: x(t) = 3t + 1,5t2
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*22 =6+6=12 м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.
Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:
- Конвертер единиц измерения расстояния (длины)
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
Загрузить PDF
Загрузить PDF
Скорость — это векторная величина, которая характеризует быстроту перемещения и направление движения предмета (тела). В математике скорость определяется как изменение положения тела в зависимости от изменения времени.[1]
Скорость можно найти во множестве физических и математических задач. Выбор правильной формулы зависит от данных значений, поэтому внимательно читайте условие задачи.
Формулы
-
1
-
2
Запишите формулу, содержащую положение и время. Скорость можно вычислить по изменению положения тела и времени. Такую формулу можно применить к любой задаче. Обратите внимание, что если скорость тела меняется, вы найдете среднюю скорость за все время движения, а не конкретную скорость в определенный момент времени.
-
3
Вычислите расстояние между начальным и конечным положениями. То есть между точками начала и окончания движения; они, наряду с направлением движения, указывают на «перемещение» или «изменение положения».[3]
При этом траектория движения тела между этими точками значения не имеет.-
Пример 1: автомобиль, едущий на восток, начинает движение в положении x = 5 м. Через 8 с машина находится в положении х = 41 м. Каково перемещение автомобиля?
- Автомобиль переместился на 41-5 = 36 м на восток.
-
Пример 2: трамплин подбрасывает пловца на 1 метр вверх, и пловец летит до воды 5 м. Каково перемещение пловца?
- Пловец оказался на 4 м ниже начальной точки, поэтому его перемещение равно -4 м (0 + 1 – 5 = -4). Несмотря на то, что пройденное пловцом расстояние составило 6 м (1 м вверх и 5 м вниз), конечная точка находится на 4 м ниже начальной точки.
-
Пример 1: автомобиль, едущий на восток, начинает движение в положении x = 5 м. Через 8 с машина находится в положении х = 41 м. Каково перемещение автомобиля?
-
4
Вычислите изменение времени. Время, которое потребовалось для достижения конечной точки, будет, скорее всего, дано в задаче; если нет, просто вычтите начальное время из конечного.
- Пример 1 (продолжение): в задаче сказано, что машине потребовалось 8 с, чтобы переместиться из начальной точки в конечную, поэтому изменение времени равно 8 с.
- Пример 2 (продолжение): если пловец прыгнул в момент времени t = 7 с и коснулся воды в момент времени t = 8 с, изменение времени: 8 – 7 = 1 с.
-
5
Разделите перемещение на изменение времени. Сделайте это, чтобы найти скорость движущегося тела. Теперь укажите направление движения, и вы получите среднюю скорость.
-
6
Решите задачу, когда направление движения меняется. Не во всех задачах тело движется вдоль одной линии. Если тело совершило поворот, нарисуйте схему движения и решите геометрическую задачу, чтобы найти расстояние.
-
Пример 3: человек бежит 3 м на восток, затем поворачивает на 90° и бежит 4 м на север. Каково перемещение человека?
- Нарисуйте схему и соедините начальную и конечную точки прямой линией. Это гипотенуза треугольника, которую можно найти с помощью теоремы Пифагора или других формул. В нашем примере перемещение составит 5 м на северо-восток.
- Возможно, учитель математики попросит вас найти точное направление движения (в виде угла над горизонтальной прямой). В этом случае воспользуйтесь геометрическими законами или векторами.[4]
Реклама
-
Пример 3: человек бежит 3 м на восток, затем поворачивает на 90° и бежит 4 м на север. Каково перемещение человека?
-
1
Запомните формулу для вычисления скорости ускоряющегося тела. Ускорение — это быстрота изменения скорости. Если ускорение постоянное, скорость меняется с одинаковой быстротой.[5]
Формула включает произведение ускорения и времени, а также начальную скорость: -
2
Умножьте ускорение на изменение времени. Так вы вычислите, насколько скорость увеличилась (или уменьшилась) за это время.
-
Пример: лодка, плывущая на север со скоростью 2 м/с, ускоряется на 10 м/с2. Насколько увеличится скорость лодки в течение 5 с?
- a = 10 м/с 2
- t = 5 с
- (a * t) = 10 * 5 = 50 м/с.
-
Пример: лодка, плывущая на север со скоростью 2 м/с, ускоряется на 10 м/с2. Насколько увеличится скорость лодки в течение 5 с?
-
3
Прибавьте начальную скорость. Вы нашли общее изменение скорости. Прибавьте это значение к начальной скорости тела, чтобы вычислить конечную скорость.
-
4
Укажите направление движения. Помните, что скорость является векторной величиной, то есть имеет направление. Поэтому в ответе укажите направление.
- В нашем примере лодка начала движение на север и не изменила направление, поэтому ее конечная скорость равна 52 м/с на север.
-
5
Используйте данную формулу, чтобы вычислить другие величины, которые входят в нее. Если известны ускорение и скорость в определенный момент времени, с помощью формулы можно найти скорость в другой момент времени. Например, вычислим начальную скорость:
- Поезд ускоряется на 7 м/с2 в течение 4 секунд и достигает скорости 35 м/с. Какова начальная скорость поезда?
Реклама
-
1
Запомните формулу для вычисления круговой скорости. Круговая скорость — это скорость, которую должно иметь тело, чтобы постоянно вращаться вокруг другого тела, обладающего гравитацией, например, планеты.[6]
- Круговая скорость равна отношению длины круглого пути к периоду времени, в течение которого тело движется.
- Формула для вычисления круговой скорости:
- v = (2πr) / T
- Обратите внимание, что 2πr — это длина окружности.
- r — радиус.
- T — период времени.
-
2
Умножьте радиус окружности на 2π. Сначала необходимо вычислить длину окружности. Для этого умножьте радиус на 2π. В качестве значения π можно использовать 3, 14.
- Пример: найдите круговую скорость тела, движущегося по круговой траектории с радиусом 8 м в течение 45 с.
- r = 8 м
- T = 45 с
- Длина окружности = 2πr ≈ (2)(3,14)(8) = 50,24 м
- Пример: найдите круговую скорость тела, движущегося по круговой траектории с радиусом 8 м в течение 45 с.
-
3
Разделите полученное значение на время. Сделайте это, чтобы вычислить круговую скорость тела.
- Пример: v = (2πr) / T = 50,24 / 45 = 1,12 м/с
- Круговая скорость тела равна 1,12 м/с.
Реклама
- Пример: v = (2πr) / T = 50,24 / 45 = 1,12 м/с
Советы
- Метры в секунду (м/с) — это единица измерения скорости.[7]
. Перед решением задачи убедитесь, что все единицы измерения соответствуют друг другу, например, значения даны в метрах (м), секундах (с), метрах в секунду (м/с) и метрах в квадратных секундах (м/с2). - Средняя скорость характеризует среднюю скорость, которую имеет тело на протяжении всего пути. Мгновенная скорость — это скорость тела в определенный момент времени.
Реклама
Об этой статье
Эту страницу просматривали 17 699 раз.
Была ли эта статья полезной?
Скорость, ускорение и время являются основными величинами для вывода уравнения движения. В общем, производная скорости по времени дает ускорение.
В кинематике скорость можно найти, используя ускорение и время. С скорость и ускорение связаны с величиной и направлением, для определения скорости мы используем как алгебраический метод, так и интегральное исчисление. В этом посте обсуждается, как найти скорость с учетом ускорения и времени, используя оба метода.
Представим, что тело движется с ускорением «а», преодолевая определенное расстояние в момент «t».
Алгебраическим методом:
Из кинематического определения ускорение – скорость изменения скорости движущегося тела.
а=в/т
Здесь мы считаем; первоначально тело обладает минимальной скоростью; следовательно, начальная скорость можно считать примерно равной нулю.
Переставляя члены, мы получаем скорость тела как;
v = а * т
Методом интегрального исчисления:
Производная по времени от скорость дает ускорение тела. Это определяется следующим уравнением.
d/dt[v(t)]= а(t)
Преобразуя приведенное выше уравнение
dv (t) = a (t) dt
Интегрируя приведенное выше уравнение по времени t
∫d/dt[v(t)]=∫a(t) dt+C
Где; C – интегральная постоянная.
Следовательно; v = при + C
Вышеприведенное уравнение дает скорость; таким образом, умножение ускорения на время дает скорость.
Как найти скорость по графику ускорения и времени?
Построен график ускорения в зависимости от времени, что позволяет определить различные физические величины, такие как рывки и удары. скорость. Область, покрытая графиком «ускорение – время», показывает скорость.
Например, машина движется с начальной скоростью 16 м / с. Как со временем, машина начинает разгоняться. В ускорение автомобиля постоянна во времени. Через некоторое время машина внезапно останавливается, что показано на приведенном ниже графике.
Пунктирная линия используется как контрольная линия, когда тело останавливается.
Площадь, занимаемая в график ускорение – время представляет собой прямоугольник. Площадь прямоугольника определяется как
А = l × b
Из приведенного выше графика длина прямоугольника – это ускорение, а ширина – время; следовательно, уравнение
А = а * т
Но площадь графика at – это скорость, тогда
v = а * т
v = 7 × 8
v = 56 м / с.
Следовательно, по определению На графике времени разгона площадь – это не что иное, как скорость.
Как найти начальную скорость с ускорением и временем?
Когда тело начинает двигаться из одной точки в другую, вначале оно обладает некоторой скоростью. Тело не нуждается постоянная скорость пока не достигнет конечного пункта назначения. Скорость тела изменяется со временем по мере его прохождения, и, следовательно, тело приобретает ускорение.
Из приведенного выше объяснения ясно, что движущееся тело может иметь разные скорости. Тела скорость на начальном этапе может отличаться от финального. Давайте обсудим нахождение скорости с ускорением и временем в начальной точке.
Рассмотрим сначала автомобиль, движущийся со скоростью vi, а его скорость изменится через некоторое время t. Теперь тело ускоряется с ускорением «а», и, наконец, когда оно достигает конечной точки, оно имеет скорость vf.
Начальную скорость можно рассчитать тремя способами.
Используя алгебраический метод:
Ускорение из-за изменения скорости определяется выражением
а = (vf-vi)/т
а * т = vf – vi
О перестановке
vi = Vf – в
Вышеприведенное уравнение дает начальную скорость движущегося тела.
По расчетам:
Исходя из определения ускорения, уравнение имеет вид
а=дв/дт
Изменение условий;
адт = дв
Интегрируя приведенное выше уравнение, выбирая пределы в качестве начальной скорости vi в момент времени t = 0 и конечной скорости vf в момент t.
а (t – 0) = (vf – vi)
при = vf – vi
Преобразуя приведенное выше уравнение, мы получаем начальную скорость.
vi = Vf – в
Графическим методом:
Построен график зависимости скорости от времени, наклон которого дает ускорение – затем, найдя наклон, можно вычислить начальную скорость.
Исходя из приведенного выше графика, мы можем сказать это.
- В единый интервал времени скорость тела изменяется.
- OD – время, затрачиваемое телом на путешествие, а BD – конечная скорость тела.
- Перпендикулярные линии от BD к A проводятся параллельно OD. Таким же образом проводится линия BE параллельно OD.
На приведенном выше графике показано, что
Начальная скорость тела vi = ОА
Конечная скорость тела vf = БД
На графике BD = BC + DC
Следовательно, vf = ВС + ПОС
Но DC = OA = vi
vf = до нашей эры + ви
На графике наклон = ускорение a
а=ВС/АС
Но AC = t (из графика)
а=БК/т
при = BC
Подставляя значение BC
vf = при + vi
vi = Vf – в
Как найти изменение скорости в зависимости от ускорения и времени
В общем, изменение скорости со временем дает ускорение.
Пусть тело движется с ускорением ‘a’ со временем ‘t’, изначально скорость объекта равна vi, а в конечной точке имеет скорость vf. Тогда изменение скорости определяется по уравнению:
∆a=(Δv/Δt)
Где ∆v – изменение скорости, а ∆t – изменение во времени.
∆v = ∆a∆t
Но изменение скорости определяется разница между начальной и конечной скоростью. Это дается уравнением ниже.
∆v = vf -vi
Изменение в скорость можно рассчитать с помощью графика “ускорение – время”. Площадь под графиком at показывает изменение скорости.
Давайте ясно поймем это, рассмотрев пример, представленный графиком, приведенным ниже.
Площадь на графике времени ускорения представляет собой треугольник. Следовательно, вычисляя изменение скорости дается путем вычисления площади треугольника. Формула для определения площади треугольника:
А=(1/2)чб
Здесь h – высота треугольника, ускорение считается высотой, а b – основание треугольника, которое определяется осью времени. Таким образом, изменение скорости равно
∆v=(1/2)*6*9
∆v = 29 м / с.
По изменению скорости мы можем узнать начальную и конечную скорость тела.
Решены задачи о том, как найти скорость с ускорением и временем.
Задача 1) Лодка движется с начальной скоростью 11 м / с. Лодка развивает ускорение 3 м / с.2 каждые 10 секунд. Затем рассчитайте изменение скорости и конечную скорость лодки.
Решение:
Данные приведены для расчета:
Начальная скорость лодки vi = 11 м / с.
Изменение ускорения, достигаемого лодкой a = 3 м / с2.
Изменение по времени t = 10 сек.
∆v = ∆a∆t
∆v = 3 × 10
∆v = 30 м / с
Чтобы найти окончательную скорость, уравнение
∆v = vf -vi
vf = ∆v + vi
vf = 30 + 11
vf = 41 м / с.
Задача 2) График ускорение – время приведен ниже. Найдите изменение скорости и вычислите начальную скорость, если конечная скорость равна 54 м / с.
Решение:
Приведенные данные:
Конечная скорость vf = 54 м / с. На графике ускорение-время покрытая область представляет собой трапецию. Таким образом, площадь трапеции определяется выражением
А=[(а+б)/2)]*ч
Где a и b – прилегающее основание трапеции, h – высота. Из графика; a = 9 единиц, b = 5 единиц, h = 4 единицы.
А=[(9+5)/2]*4
А = 28 шт.
Изменение скорости равно площади трапеции.
∆v = 28 м / с.
Чтобы найти начальную скорость
∆v = vf -vi
vi = Vf – ∆v
vi = 54 – 28
vi = 26 м / с.
Задача 3) дается график ускорение – время для определения изменения скорости.
Решение:
Приведенный выше график можно разделить на три части, представленные пунктирной линией, как показано на рисунке ниже.
На приведенном выше графике можно понять следующие термины.
OAD и BCE – треугольник; площадь треугольника задается формулой
а=(1/2)чб
ABCD – прямоугольник; площадь прямоугольника определяется выражением
А = l × b
Чтобы найти изменение скорости, необходимо вычислить сумму площадей всех геометрических структур.
∆v = A=(1/2)hb+lb+(1/2)hb
Изменение скорости ∆v = 180 м / с.
Задача 4) Найдите начальную скорость мяча, который ускоряется со скоростью 6 м / с.2 со временем 8 сек. Конечная скорость мяча составляет 100 м / с.
Решение:
Приведены данные: ускорение мяча a = 6 м / с2.
Время t = 8 сек.
Конечная скорость vf = 100 м / с.
Для нахождения начальной скорости тела задается уравнение
vi = Vf – в
vi = 100 – (6 × 8)
vi = 100 – 48
vi = 52 м / с.
Задача 5) Рассчитайте изменение скорости движущегося объекта, имеющего начальную скорость 34 м / с. Ускорение объекта 12 м / с.2, а изменение по времени – 7 сек.
Решение:
Данный:
Начальная скорость объекта vi = 34 м / с.
Ускорение объекта a = 12 м / с2.
Изменение по времени t = 7 сек.
Конечная скорость объекта определяется выражением;
vf = Vi + в
vf = 34 + (12 * 7)
vf = 34 + 84
vf = 118 м / с.
Изменение скорости определяется выражением;
∆v = vf – vi
∆v = 118 – 34
∆v = 84 м / с.
Задача 6) Диск движется с начальной скоростью 25 м / с. Диск меняет свою скорость каждые 10 секунд. Изменение ускорения 5 м / с.2. Рассчитайте конечную скорость диска.
Решение:
Приведенные данные:
Начальная скорость диска vi = 25 м / с.
Изменение ускорения ∆a = 5 м / с2.
Изменение времени ∆t = 10 сек.
Изменение скорости равно
∆v = ∆a∆t
∆v = 5 × 10
∆v = 50 м / с.
Конечная скорость диска может быть рассчитана по формуле, приведенной ниже.
∆v = vf – vi
50 = вf -25
vf = 50 + 25
vf = 75 м / с.