Как найти скорость физика все формулы - Сайт, где вы сможете решить свои вопросы

Скорость
${vec v}={frac {{mathrm {d}}{vec r}}{{mathrm {d}}t}}$
Размерность	LT⁻¹
Единицы измерения
СИ	м/с
СГС	см/с
Примечания
вектор

Классическая механика
История…
Фундаментальные понятия Пространство Время Масса Скорость Сила Механическая работа Энергия Импульс
Формулировки Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби Уравнения Рауса Уравнения Аппеля Теория Купмана — фон Неймана
Разделы Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика
Учёные Галилей Кеплер Ньютон Эйлер Лаплас Д’Аламбер Лагранж Гамильтон Коши
См. также: Портал:Физика

Ско́рость (стандартное обозначение: , от англ. velocity, исходно от лат. vēlōcitās) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта. По определению, равна производной радиус-вектора точки по времени^[1]. В СИ измеряется в метрах в секунду.

В русском языке этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, то есть проекцию вектора на касательную к траектории точки^[2]. В некоторых других языках для скалярной скорости имеются отдельные наименования, например англ. speed, лат. celeritas^{[значимость факта?]}.

Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.

Понятие «скорость» в классической механике[править | править код]

Случай материальной точки[править | править код]

Вектор скорости (мгновенной скорости) материальной точки в каждый момент времени определяется как производная по времени радиус-вектора текущего положения этой точки, так что^[3]:

${vec v}={{mathrm {d}}{{vec r}} over {mathrm {d}}t}equiv v_{{tau }}{{vec tau }},$

где — единичный вектор касательной, проходящей через текущую точку траектории (он направлен в сторону возрастания дуговой координаты движущейся точки), а $v_{{tau }}equiv {dot {s}}$ — проекция вектора скорости на направление упомянутого единичного вектора, равная производной дуговой координаты по времени и именуемая алгебраической скоростью точки. В соответствии с приведёнными формулами, вектор скорости точки всегда направлен вдоль касательной, а алгебраическая скорость точки может отличаться от модуля этого вектора лишь знаком^[4]. При этом:

Пройденный точкой путь за промежуток времени от t_0 до , находится как

${displaystyle {tilde {s}}=int _{t_{0}}^{t}|{dot {s}}|,mathrm {d} t;}$

Когда алгебраическая скорость точки всё время неотрицательна, путь совпадает с приращением дуговой координаты за время от t_0 до (если же при этом начало отсчёта дуговой координаты совпадает с начальным положением движущейся точки, то будет просто совпадать с ).

Иллюстрация средней и мгновенной скорости

Если алгебраическая скорость точки не меняется с течением времени (или, что то же самое, модуль скорости постоянен), то движение точки называется^[5] равномерным (алгебраическое касательное ускорение при этом тождественно равно нулю).

Предположим, что . Тогда при равномерном движении скорость точки (алгебраическая) будет равна отношению пройденного пути к промежутку времени $t-t_{0}$ , за который этот путь был пройден:

${{dot {s}}}^{{,{mathrm {cp}}}}={{tilde {s}} over t-t_{0}};.$

В общем же случае аналогичные отношения

${{vec v}}^{{,,{mathrm {cp}}}}={{{vec r}}-{{vec r}}_{0} over t-t_{0}}equiv {Delta {{vec r}} over Delta {t}}$

и ${{dot {s}}}^{{,{mathrm {cp}}}}={s-s_{0} over t-t_{0}}equiv {Delta {s} over Delta {t}}$

определяют соответственно среднюю скорость точки^[6] и её среднюю алгебраическую скорость; если термином «средняя скорость» пользуются, то о величинах и говорят (чтобы избежать путаницы) как о мгновенных скоростях.

Различие между двумя введёнными выше понятиями средней скорости состоит в следующем. Во-первых, ${{vec v}}^{{,,{mathrm {cp}}}}$ — вектор, а ${{dot {s}}}^{{,{mathrm {cp}}}}$ — скаляр. Во-вторых, эти величины могут не совпадать по модулю. Так, пусть точка движется по винтовой линии и за время своего движения проходит один виток; тогда модуль средней скорости этой точки будет равен отношению шага винтовой линии (то есть расстояния между её витками) ко времени движения, а модуль средней алгебраической скорости — отношению длины витка ко времени движения.

Случай тела конечных размеров[править | править код]

Для тела протяжённых размеров понятие «скорости» (тела как такового, а не одной из его точек) не может быть определено; исключение составляет случай мгновенно-поступательного движения. Говорят, что абсолютно твёрдое тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны^[7]; тогда можно, разумеется, положить скорость тела равной скорости любой из его точек. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем же случае скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса модули скоростей точек на ободе относительно дороги принимают значения от нуля (в точке касания с дорогой) до удвоенного значения скорости центра колеса (в точке, диаметрально противоположной точке касания). Распределение скоростей точек абсолютно твёрдого тела описывается кинематической формулой Эйлера.

Начальная скорость[править | править код]

Начальная скорость ( ${displaystyle {vec {v}}_{0}}$ ) — это скорость материальной точки в момент, принимаемый за нуль по шкале времени (то есть при t = 0 )^[8].

Истолкование ${displaystyle {vec {v}}_{0}}$ как скорости, с которой тело начинает движение, не вполне корректно, поскольку покоившееся тело в принципе не может начать двигаться с отличной от нуля скоростью. При такой формулировке неявно подразумевается, что в короткий промежуток времени действовала большая по величине сила, на пренебрежимо малом участке разогнавшая тело до скорости ${displaystyle {vec {v}}={vec {v}}_{0}}$ к моменту t = 0 .

Запись скорости в разных системах координат[править | править код]

В декартовых координатах[править | править код]

В прямоугольной декартовой системе координат^[9]:

${displaystyle mathbf {v} =v_{x}mathbf {i} +v_{y}mathbf {j} +v_{z}mathbf {k} .}$

При этом , следовательно,

${displaystyle mathbf {v} ={frac {mathrm {d} (xmathbf {i} +ymathbf {j} +zmathbf {k} )}{mathrm {d} t}}={frac {mathrm {d} x}{mathrm {d} t}}mathbf {i} +{frac {mathrm {d} y}{mathrm {d} t}}mathbf {j} +{frac {mathrm {d} z}{mathrm {d} t}}mathbf {k} .}$

Таким образом, компоненты вектора скорости — это скорости изменения соответствующих координат материальной точки^[9]:

${displaystyle v_{x}={frac {mathrm {d} x}{mathrm {d} t}};v_{y}={frac {mathrm {d} y}{mathrm {d} t}};v_{z}={frac {mathrm {d} z}{mathrm {d} t}}.}$

В цилиндрических координатах[править | править код]

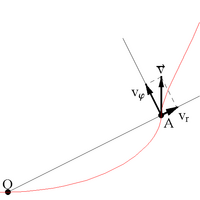
Скорость в полярных координатах

В цилиндрических координатах ^[9]:

${displaystyle v_{R}={frac {mathrm {d} R}{mathrm {d} t}};v_{varphi }=R{frac {mathrm {d} varphi }{mathrm {d} t}};v_{z}={frac {mathrm {d} z}{mathrm {d} t}}.}$

$v_{varphi }$ носит название поперечной скорости, $v_{R}$ — радиальной.

В сферических координатах[править | править код]

В сферических координатах ^[9]:

${displaystyle v_{R}={frac {mathrm {d} R}{mathrm {d} t}};v_{varphi }=Rsin theta {frac {mathrm {d} varphi }{mathrm {d} t}};v_{theta }=R{frac {mathrm {d} theta }{mathrm {d} t}}.}$

Для описания плоского движения иногда используются полярные координаты, которые можно рассматривать как частный случай цилиндрических (c const) или сферических (с ).

Физическая и координатная скорости[править | править код]

В аналитической механике вышеприведённые и другие криволинейные координаты играют роль обобщённых координат; изменение положение тела описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями (они могут иметь размерность отличную от м/c). Физической же скоростью является производная радиус-вектора по времени, а её составляющие в каждом случае задаются всем стоящим перед соответствующим ортом выражением.

Некоторые связанные со скоростью понятия[править | править код]

Ряд величин в классической механике выражается через скорость.

Импульс, или количество движения, — это мера механического движения точки, которая определяется как произведение массы точки на её скорость

Импульс является векторной величиной, его направление совпадает с направлением скорости. Для замкнутой системы выполняется закон сохранения импульса.

От скорости также зависит кинетическая энергия механической системы. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения^[10]^[11]:

${displaystyle T={frac {mv^{2}}{2}}+{frac {{mathcal {I}}{vec {omega }}^{2}}{2}},}$

где — масса тела, — скорость центра масс тела, — момент инерции тела, — угловая скорость тела.

Изменение скорости во времени характеризуется ускорением. Ускорение отражает изменение скорости как по величине (тангенциальное ускорение), так и по направлению (центростремительное ускорение)^[12]:

${vec a}={frac {{mathrm {d}}{vec v}}{{mathrm {d}}t}}={vec a}_{tau }+{vec a}_{n}={frac {{mathrm {d}}|{vec v}|}{{mathrm {d}}t}}{vec e}_{tau }+{v^{2} over r}{vec e}_{n},$

где — радиус кривизны траектории точки.

Преобразования Галилея и Лоренца для скорости[править | править код]

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта была равна , а скорость системы отсчёта относительно системы отсчёта равна vec u , то скорость тела при переходе в систему отсчёта будет равна^[9]

{displaystyle {vec {v}}'={vec {v}}-{vec {u}}.}

Для скоростей, близких к скорости света, преобразования Галилея становятся несправедливы. При переходе из системы в систему необходимо использовать преобразования Лоренца для скоростей^[9]:

$v_{x}'={frac {v_{x}-u}{1-(v_{x}u)/c^{2}}},v_{y}'={frac {v_{y}{sqrt {1-{frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},v_{z}'={frac {v_{z}{sqrt {1-{frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},$

в предположении, что скорость vec u направлена вдоль оси системы . В пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Скорость в релятивистской механике[править | править код]

Четырёхмерная скорость[править | править код]

Одним из обобщений понятия скорости является четырёхмерная скорость (скорость в релятивистской механике^[9]). В специальной теории относительности каждому событию ставится в соответствие точка пространства Минковского, три координаты которого представляют собой декартовы координаты трёхмерного евклидова пространства, а четвёртая ― временну́ю координату , где ― скорость света, ― время события. Компоненты четырёхмерного вектора скорости связаны с проекциями трёхмерного вектора скорости следующим образом^[9]:

$v_{0}={frac {c}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{1}={frac {v_{x}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{2}={frac {v_{y}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{3}={frac {v_{z}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}.$

Четырёхмерный вектор скорости является времениподобным вектором, то есть лежит внутри светового конуса^[9].

Существует также понятие четырёхимпульс, временна́я компонента которого равна E/c (где — энергия). Для четырёхмерного импульса выполняется равенство^[13]:

${displaystyle p_{i}=m,v_{i}}$

где $v_{i}$ — четырёхмерная скорость.

Понятие «быстрота»[править | править код]

В релятивистской механике угол между касательной к мировой линии частицы и осью времени в базовой системе отсчёта носит название быстроты (обозначается theta ). Быстрота выражается формулой

$theta =c,{mathrm {Arth}},{frac {v}{c}}={frac {c}{2}}ln {frac {1+{dfrac {v}{c}}}{1-{dfrac {v}{c}}}},$

где — ареатангенс, или гиперболический арктангенс. Быстрота стремится к бесконечности когда скорость стремится к скорости света. В отличие от скорости, для которой необходимо пользоваться преобразованиями Лоренца, быстрота аддитивна, то есть

$theta '=theta +theta _{0},$

где $theta _{0}$ — быстрота системы отсчёта относительно системы отсчёта .

Некоторые скорости[править | править код]

Космические скорости[править | править код]

Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос

Небесная механика изучает поведение тел Солнечной системы и других небесных тел. Движение искусственных космических тел изучается в астродинамике. При этом рассматривается несколько вариантов движения тел, для каждого из которых необходимо придание определённой скорости. Для вывода спутника на круговую орбиту ему необходимо придать первую космическую скорость (например, искусственный спутник Земли); преодолеть гравитационное притяжение позволит вторая космическая скорость (например, объект запущенный с Земли, вышедший за её орбиту, но находящийся в Солнечной системе); третья космическая скорость нужна чтобы покинуть звёздную систему, преодолев притяжение звезды (например, объект запущенный с Земли, вышедший за её орбиту и за пределы Солнечной системы); четвёртая космическая скорость позволит покинуть галактику.

В небесной механике под орбитальной скоростью понимают скорость вращения тела вокруг барицентра системы.

Скорости распространения волн[править | править код]

Скорость звука[править | править код]

Скорость звука — скорость распространения упругих волн в среде, определяется упругостью и плотностью среды. Скорость звука не является постоянной величиной и зависит от температуры (в газах), от направления распространения волны (в монокристаллах). При заданных внешних условиях обычно не зависит от частоты волны и её амплитуды. В тех случаях, когда это не выполняется и скорость звука зависит от частоты, говорят о дисперсии звука. Впервые измерена Уильямом Дерхамом. Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твёрдых телах, поэтому при сжижении газа скорость звука возрастает.

Отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде называется числом Маха по имени австрийского учёного Эрнста Маха. Упрощённо, скорость, соответствующая 1 Маху при давлении в 1 атм (у земли на уровне моря), будет равна скорости звука в воздухе. Движение аппаратов со скоростью, сравнимой со скоростью звука, сопровождается рядом явлений, которые называются звуковой барьер. Скорости от 1,2 до 5 Махов называются сверхзвуковыми, скорости выше 5 Махов — гиперзвуковыми.

Скорость света[править | править код]

Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 секунды.

Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме. Традиционно обозначается латинской буквой «c» (произносится как [це]). Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.

Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. Теперь ввиду современного определения метра скорость света считается равной точно 299792458 м/с^[14].

Скорость гравитации[править | править код]

Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн. До сих пор остаётся не определённой экспериментально, но согласно общей теории относительности должна совпадать со скоростью света.

Единицы измерения скорости[править | править код]

Линейная скорость:

Метр в секунду, (м/с), производная единица системы СИ
Километр в час, (км/ч)
узел (морская миля в час)
Число Маха, 1 Мах равен скорости звука; Max n в n раз быстрее. Как единица, зависящая от конкретных условий, должна дополнительно определяться.
Скорость света в вакууме (обозначается c)

Угловая скорость:

Радианы в секунду, принята в системах СИ и СГС. Физическая размерность 1/с.
Обороты в секунду (в технике)
градусы в секунду, грады в секунду

Соотношения между единицами скорости[править | править код]

1 м/с = 3,6 км/ч
1 узел = 1,852 км/ч = 0,514 м/c
Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
c = 299 792 458 м/c

Исторический очерк[править | править код]

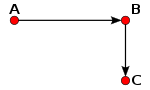
Две стадии движения брошенного тела по теории Авиценны: отрезок АВ — период «насильственного стремления», отрезок ВС — период «естественного стремления» (падение вертикально вниз)

Автолик из Питаны в IV веке до н. э. определил равномерное движение так: «О точке говорится, что она равномерно перемещается, если в равные времена она проходит равные и одинаковые величины». Несмотря на то, что в определении участвовали путь и время, их отношение считалось бессмысленным^[15], так как сравнивать можно было только однородные величины и скорость движения являлась чисто качественным, но не количественным понятием^[16]. Живший в то же время Аристотель делил движение на «естественное», когда тело стремится занять своё естественное положение, и «насильственное», происходящее под действием силы. В случае «насильственного» движения произведение величины «двигателя» и времени движения равно произведению величины «движимого» и пройденного пути, что соответствует формуле Ft=ms , или F=mv ^[15]. Этих же взглядов придерживался Авиценна в XI веке, хотя и предлагал другие причины движения^[17], а также Герард Брюссельский в конце XII —
начале XIII века. Герард написал трактат «О движении» — первый европейский трактат по кинематике — в котором сформулировал идею определения средней скорости движения тела (при вращении прямая, параллельная оси вращения, движется «одинаково с любой своей точкой», а радиус — «одинаково со своей серединой»)^[18].

В 1328 году увидел свет «Трактат о пропорциях или о пропорциях скоростей при движении» Томаса Брадвардина, в котором он нашёл несоответствие в физике Аристотеля и связи скорости с действующими силами. Брадвардин заметил, что по словесной формуле Аристотеля если движущая сила равна сопротивлению, то скорость равна 1, в то время как она должна быть равна 0. Он также представил свою формулу изменения скорости, которая хоть и была не обоснована с физической точки зрения, но представляла собой первую функциональную зависимость скорости от причин движения. Брадвардин называл скорость «количеством движения»^[19]. Уильям Хейтсбери, в трактате «О местном движении» ввёл понятие мгновенной скорости. В 1330—1340 годах он и другие ученики Брадвардина доказали так называемое «мертонское правило», которое означает равенство пути при равноускоренном движении и равномерном движении со средней скоростью^[20].

Всякая широта движения, униформно приобретаемая или теряемая, соответствует своему среднему градусу, так что столько же в точности будет пройдено благодаря этой приобретаемой широте, сколько и благодаря среднему градусу, если бы тело двигалось всё время с этим средним градусом.

— «Мертонское правило» в формулировке Суайнсхеда^[20]

В XIV веке Жан Буридан ввёл понятие импетуса^[21], благодаря чему была определена величина изменения скорости — ускорение. Николай Орем, ученик Буридана, предложил считать, что благодаря импетусу ускорение остаётся постоянным (а не скорость, как полагал сам Буридан), предвосхитив, таким образом, второй закон Ньютона^[22]. Орем также использовал графическое представление движения. В «Трактате о конфигурации качеств и движения» (1350) он предложил изображать отрезками перпендикулярных прямых количество и качество движения (время и скорость), иными словами, он нарисовал график изменения скорости в зависимости от времени^[23].

По мнению Тартальи, только вертикальное падение тела является «естественным» движением, а все остальные — «насильственные», при этом у первого типа скорость постоянно возрастает, а у второго — убывает. Два этих типа движения не могут проистекать одновременно. Тарталья считал, что «насильственные» движения вызваны ударом, результатом которого является «эффект», определяемый скоростью^[24]. С критикой работ Аристотеля и Тартальи выступал Бенедетти, который вслед за Оремом пользовался понятиями импетуса и ускорения^[25].

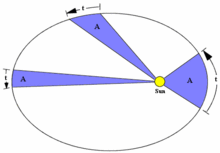
В 1609 году в работе «Новая астрономия» Кеплер сформулировал закон площадей, согласно которому секторная скорость планеты (площадь, описываемая отрезком планета — Солнце, за единицу времени) постоянна^[26]. В «Началах философии» Декарт сформулировал закон сохранения количества движения, которое в его понимании есть произведение количества материи на скорость^[27], при этом Декарт не принимал во внимание тот факт, что количество движения имеет не только величину, но и направление^[28]. В дальнейшем понятие «количество движения» развивал Гук, который понимал его как «степень скорости, присущей в определённом количестве вещества»^[29]. Гюйгенс, Валлис и Рен добавили к этому определению направление. В таком виде во второй половине XVII века количество движения стало важным понятием в динамике, в частности в работах Ньютона и Лейбница^[30]. При этом Ньютон не определял в своих работах понятие скорости^[31]. По-видимому, первая попытка явного определения скорости была сделана Валлисом в его трактате «Механика или геометрический трактат о движении» (1669—1671): «Скорость есть свойство движения, отражающееся в сравнении длины и времени; а именно, она определяет, какая длина в какое время проходится»^[32].

В XVII веке были заложены основы математического анализа, а именно интегрального и дифференциального исчисления. В отличие от геометрических построений Лейбница, теория «флюксий» Ньютона строится на потребностях механики и имеет в своём основании понятие скорости. В своей теории Ньютон рассматривает переменную величину «флюенту» и её скорость изменения — «флюксию»^[33].

Скорости в природе и технике[править | править код]

Основной источник: ^[34]

	Метры в секунду
Скорость улитки	${displaystyle 1{,}4times 10^{-2}}$
Скорость черепахи	${displaystyle 5{,}0times 10^{-2}}$
Средняя скорость здорового человека (произвольный темп)
Рекорд скорости человека в ходьбе на 50 км	()
Рекорд скорости человека в беге на дистанции 100 м	${displaystyle 1{,}0times 10^{1}}$ ( ${displaystyle 1{,}044times 10^{1}}$ )
Скорость гепарда
Максимальная скорость полёта сокола
Максимальная скорость локомотива на железной дороге
Максимальная скорость автомобиля	^[35]
Средняя скорость молекулы азота при температуре 0 °C
Максимальная скорость пассажирского реактивного самолёта
Скорость движения Луны по орбите вокруг Земли
Скорость искусственного спутника Земли
Скорость движения Земли по орбите вокруг Солнца
Скорость движения Солнца по орбите вокруг центра Галактики
Скорость электронов в кинескопе телевизора	${displaystyle 1{,}0times 10^{8}}$
Скорость движения самых далёких галактик	${displaystyle 1{,}4times 10^{8}}$
Максимальная скорость протонов в Большом адронном коллайдере	299 792 455
Скорость частицы Oh-My-God	299792457,9999999999999985310169558
Скорость безмассовых частиц (фотонов, глюонов, гравитонов)	299 792 458
Скорость тахионов и сверхбрадионов	> 299792458

Скорости движения живых существ[править | править код]

Сапсан (самое быстрое животное): самая высокая зарегистрированная скорость — 389 км/ч^[36];
Гепард (самое быстрое наземное животное): самая высокая зарегистрированная скорость — 98 км/ч^[37];
Меч-рыба: от 100 до 130 км в час^[37];
Чёрный марлин: самая высокая зарегистрированная скорость — 105 км/ч^[36];
Вилорогая антилопа: самая высокая зарегистрированная скорость — 88,5 км/ч^[36];
Лошадь (американский квортерхорс): 88 км/ч^[36];
Человек: самая высокая зарегистрированная скорость — 44,72 км/ч (Усэйн Болт)^[37].

Рекорды скорости транспортных средств[править | править код]

Самый быстрый рукотворный объект — Parker Solar Probe, 150 км/с (относительно Солнца) в 2021 году^[38].

Абсолютный рекорд скорости в воздухе был поставлен в 1976 году американским самолетом-разведчиком Lockheed SR-71 Blackbird — 3529,56 км/ч.

Рекорд скорости на земле был установлен в 2003 году на ракетных санях и составил 10 325 км/ч или 2868 м/с (по другим данным, 10 430 км/ч)^[39]

Самая высокая скорость на наземном управляемом транспортном средстве была достигнута на реактивном автомобиле Thrust SSC в 1997 году — 1228 км/ч.

Рекорд скорости на воде был поставлен в 1978 году австралийским судном с реактивным газотурбинным двигателем Spirit of Australia^[en] — 511,11 км/ч^[40]

См. также[править | править код]

Кинематика

Примечания[править | править код]

↑ Маркеев, 1990, с. 15.
↑ Старжинский, 1980, с. 154.
↑ Маркеев, 1990, с. 15—17.
↑ Старжинский, 1980, с. 154—155.
↑ Старжинский, 1980, с. 163.
↑ Старжинский, 1980, с. 152.
↑ Маркеев, 1990, с. 46—47.
↑ См. Всегда ли начальная скорость равна нулю? в справочнике «Студворк».
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ Скорость // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Главный редактор А. М. Прохоров. Кинетическая энергия // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
↑ Главный редактор А. М. Прохоров. Вращательное движение // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
↑ Главный редактор А. М. Прохоров. Ускорение // Физический энциклопедический словарь.. — 1983. Физическая энциклопедия
↑ Главный редактор А. М. Прохоров. Импульс // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
↑ Определение метра Архивная копия от 26 июня 2013 на Wayback Machine (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
↑ ¹ ² Яковлев, 2001, с. 21.
↑ Яковлев, 2001, с. 34.
↑ Яковлев, 2001, с. 29.
↑ Яковлев, 2001, с. 31—32.
↑ Яковлев, 2001, с. 32—34.
↑ ¹ ² Яковлев, 2001, с. 35.
↑ Яковлев, 2001, с. 35—36.
↑ Яковлев, 2001, с. 37.
↑ Яковлев, 2001, с. 37—38.
↑ Яковлев, 2001, с. 43.
↑ Яковлев, 2001, с. 45.
↑ Яковлев, 2001, с. 51—52.
↑ Яковлев, 2001, с. 59.
↑ Яковлев, 2001, с. 68.
↑ Яковлев, 2001, с. 77.
↑ Яковлев, 2001, с. 91.
↑ Яковлев, 2001, с. 96.
↑ Яковлев, 2001, с. 72—73.
↑ Яковлев, 2001, с. 64—66.
↑ Кабардин О.Ф., Орлов В.А., Пономарёва А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 44
↑ FIA World Land Speed Records (англ.). Federation Internationale de l’Automobile (10 июня 2012). Дата обращения: 3 декабря 2020. Архивировано 31 марта 2019 года.
↑ ¹ ² ³ ⁴ 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 29 июля 2021 года.
↑ ¹ ² ³ 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 22 сентября 2020 года.
↑ Самый быстрый объект, созданный человеком. Зонд Parker Solar Probe развил скорость около 150 км/с. Дата обращения: 17 июня 2022. Архивировано 17 мая 2021 года.
↑ Test sets world land speed record. www.af.mil. Дата обращения: 19 апреля 2016.
↑ Назло рекордам: почему люди не хотят передвигаться очень быстро

Литература[править | править код]

Маркеев А. П. Теоретическая механика. — М.: Наука, 1990. — 416 с. — ISBN 5-02-014016-3.
Старжинский В. М. Теоретическая механика. — М.: Наука, 1980. — 464 с.
Яковлев В. И. Предыстория аналитической механики. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — 328 с. — ISBN 5-93972-063-3.

Источник

Содержание:

Определение и формула скорости
Скорость в разных системах координат
Частные случаи формул для вычисления скорости
Единицы измерения скорости
Примеры решения задач

Определение и формула скорости

Определение

Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора
$bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v.
Это векторная величина. Математически определение вектора мгновенной скорости записывается как:

$$bar{v}=frac{d bar{r}}{d t}=dot{bar{r}}(1)$$

Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения.
Модуль скорости можно определить как первую производную от длины пути (s) по времени:

$$v=frac{d s}{d t}=dot{s}(2)$$

Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.

Скорость в разных системах координат

Проекции скорости на оси декартовой системы координат запишутся как:

$$v_{x}=dot{x} ; v_{y}=dot{y} ; v_{z}=dot{z}(3)$$

Следовательно, вектор скоростив декартовых координатах можно представить:

$$bar{v}=dot{x} bar{i}+dot{y} bar{j}+dot{z} bar{k}(4)$$

где $bar{i}, bar{j}, bar{k}$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:

$$v=sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}}(5)$$

В цилиндрических координатах модуль скорости вычисляют при помощи формулы:

$$v=sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}}(6)$$

в сферической системе координат:

$$v=sqrt{(r)^{2}+(r dot{theta})^{2}+(r dot{varphi} sin theta)^{2}}(7)$$

Частные случаи формул для вычисления скорости

Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const).
При равномерном движении скорость можно вычислить, применяя формулу:

$$v=frac{s}{t}(8)$$

где s– длина пути, t – время, за которое материальная точка преодолела путь s.

При ускоренном движении скорость можно найти как:

$$bar{v}=int_{t_{1}}^{t_{2}} bar{a} d t(9)$$

где $bar{a}$ – ускорение точки,
$t_{1} leq t leq t_{2}$ – отрезок времени, в течение которого рассматривается скорость.

Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:

$$bar{v}=bar{v}_{0}+bar{a} t$$

где $bar{v}_0$ – начальная скорость движения,
$bar{a} = const$ .

Единицы измерения скорости

Основной единицей измерения скорости в системе СИ является: [v]=м/с²

В СГС: [v]=см/с²

Примеры решения задач

Пример

Задание. Движение материальной точки А задано уравнением:
$x=2 t^{2}-4 t^{3}$ . Точка начала свое движение при
t₀=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.

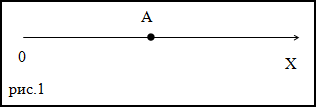
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для
этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:

$$v=frac{d x}{d t}=4 t-12 t^{2}(1.1)$$

Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент
времении сравним результат с нулем:

$$v(t=0,5)=4 cdot 0,5-12(0,5)^{2}=-1 lt 0$$

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Скорость материальной точки является функцией от времени вида:

$$v=10left(1-frac{t}{5}right)$$

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии
10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:

$$x=int_{0}^{t} v d t=int_{0}^{t} 10left(1-frac{t}{5}right) d t=10 t-frac{10 t^{2}}{2 cdot 5}=10 t-t^{2}(2.1)$$

Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:

$$x=10 cdot 10-(10)^{2}=0(m)$$

Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат
приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:

$$
begin{array}{c}
10 t-t^{2}=10(2.2) \
t_{1}=5+sqrt{15} approx 8,8(c) ; t_{2}=5-sqrt{15} approx 1,13(c)
end{array}
$$

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:

$$10 t-t^{2}=-10(2.3)$$

При решении уравнения (2.3) нам подойдет корень равный:

$$t_{3}=5+6=11 (c)$$

Ответ. 1) $x=0 mathrm{~m}$ 2) $t_{1}=8,8 mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$

Читать дальше: Формула средней скорости.

Источник

Все основные формулы по школьной физике, которые помогут для подготовке к ЕГЭ, а также для решения задач в 7, 8, 9, 10 и 11 классах. Все формулы структурированы, что позволит из запомнить гораздо быстрее.

Равномерное движение
S= U∙t, U= S/t, t=S/U	Уравнение движения при равномерном движении? где U-скорость, t-время, S-расстояние
x=x₀+U₀t	Координата при равномерном прямолинейном движении
Равномерное движение по окружности
T=t/N, T=1/v, Т=2π/ω T=2πR/U, T=2π ∙√(R/a)	T – период N – количество оборотов
v=1/T, v=ω/2π, v=U/2πR, v=1/2π ∙√(a/R), v=N/t, v=L/t	v – частота R – радиус окружности
ω=2π/Т, ω=2πv, ω=φ/t ω=U/R, ω=√(a/R)	ω – угловая скорость t – время
υ=2πR/Т, υ=2πvR, U=ωR U=√(a/R), U=L/t	U – линейная скорость тела
a=υ²/R, a=ω²R, a=Uω a=4π²R/T²	a – центростремительное ускорение
L=φR	L – длина дуги окружности (φ – угол поворота (в радианах))
Равноускоренное движение
X=X₀+υ₀∙t+(a∙t²)/2	Уравнение прямолинейного равноускоренного движения
S=U₀t+a∙t²/2 S= (υ²-υ₀²) /2а S= (υ+υ₀) ∙t /2 = U_ср∙t	Расстояние при равноускоренном движении
υ=υ₀+a∙t	Rонечная скорость тела при равноускоренном движении
a=(υ-υ₀)/t	Ускорение
U=√(2gh) t_{падения}=√(2h/g) S=U∙√(2h/g)	— Падение тела с высоты — Горизонтальный бросок (h-высота падения, g – ускорение свободного падения 9,8м/с², t-время падения, S-расстояние)
h_max=U₀²/2g	Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью U₀
t_{подъема}=U₀/g	Время подъема тела на максимальную высоту
t_полета=2U₀/g	Полное время полета (до возвращения в исходную точку)
S_торм=U₀²/2a	Тормозной путь тела двигавшегося до начала торможения со скоростью U₀ , а затем тормозившего с ускорением а
U = √(U₀²+(gt)²) tgβ = U_y/Ux = gt/U₀	Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту
h_max=(U₀∙sinα)²/2g t_{подъема}=(U₀∙sinα)/g	Бросок с земли на землю под углом к горизонту равным α. Время подъема до высшей точки и максимальная высота
S_x=U_x∙t_полетаS=U₀∙cosα∙t_полета S=U₀²∙sin2α/g t_полета=2U₀²∙sinα/g	Полное время и дальность полета при броске под углом к горизонту
Импульс
p=mυ	Импульс тела
Ft=∆p	Импульс силы
F=∆p/∆t	Второй закон Ньютона в импульсной форме
p_k=p_n	Закон сохранения импульса: в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется
Энергия
A=F∙S∙cosα	Механическая работа (F – сила, S – путь,  – угол между направлением движения и силой)
P=A/t=F∙υ	Мощность (если мощность переменная, то рассчитывается средняя мощность)
Eп=mgh	Потенциальная энергия тела, поднятого над землей
Eп=kx²/2	Потенциальная энергия упруго деформированного тела
η=Aп/Аз	Коэффициент полезного действия
Ek=mυ²/2	Кинетическая энергия тела
Молекулярная физика
ρ=m/V	Плотность (ρ – его плотность, m – масса вещества, V – объем)
ν=N/ Na = m/M	Количество вещества (N – число частиц вещества, содержащееся в массе вещества m, Na – число Авогадро, m0 – масса одной молекулы вещества, M – молярная масса)
М=m/ν	Молярная масса
m₀=m/N=M/Na	Масса одной молекулы вещества
P=nkT=1/3nm₀υ²pV=NkT	Основное уравнение молекулярно-кинетической теории идеального газа (p – давление газа, n = N/V – концентрация его молекул, m0 – масса одной молекулы, Uкв – средняя квадратичная скорость)
U_кв=√(3kT/m₀), U_кв=√(3RT/M)	Cредняя квадратичная скорость
Ek=3/2∙kT	Средняя кинетическая энергия поступательного движения одной молекулы (k – постоянная Больцмана, T – абсолютная температура)
kNa=R	Связь универсальной газовой постоянной и постоянной Авогадро
PV=m/M∙RT	Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)
PV=const (m=const и T= const)	Газовые законы. Закон Бойля-Мариотта (изотермический процесс)
V/T=const (m=const и p= const)	Газовые законы. Закон Гей-Люссака (изобарный процесс)
P/T =const (m=const и V= const)	Газовые законы. Закон Шарля (изохорный процесс)
PV/T=const (m=const )	Газовые законы. Универсальный газовый закон (Клапейрона)
V=Vo(1+λt)	Тепловое расширение газов описывается законом Гей-Люссака. (V – объем жидкости при 0 °С, V – при температуре t , λ – коэффициент объемного расширения жидкости)
l=lo(1+αt) S=So(1+2αt) V=Vo(1+3αt)	Изменение линейных размеров, площади и объема тела (lo, So , Vo – соответственно длина, площадь поверхности и объем тела при 0 °С, α – коэффициент линейного расширения тела)
Динамика
Первый закон Ньютона	Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения
F=ma	Второй закон Ньютона (F – сила, m – масса, а – ускорение).
F_1-2= — F_2-1	Третий закон Ньютона (сила действия равна силе противодействия)
F_упр = kx	Сила упругости (k – жесткость пружины, х – величина растяжения (или сжатия) пружины, оно равно разности между конечной и начальной длиной деформируемой пружины)
Fy=-kx	Закон Гука
F_{тр.скольжения}=F_{тр.макс} = μТ	Сила трения скольжения ( μ– коэффициент трения, N – сила реакции опоры.)
F=mg F=G∙M∙m/r²g=G∙M/R_n²	Сила тяжести — Закон Всемирного тяготения (G – гравитационная постоянная, F – сила с которой притягивается тело массой m к телу или планете массой M, r – расстояние между центрами этих тел)
g_h= GM/(R_n+h)² = g_h= gR_n²/(R_n+h)²	Ускорение свободного падения на некоторой высоте от поверхности планеты (h – высота над поверхностью планеты)
U= √(GM/(R_n+h)) U= √(gR_n²/(R_n+h))	Скорость спутника на круговой орбите радиусом r = R_n + h
U=√(gR_n)	Первая космическая скорость (скорость движения спутника по орбите вблизи поверхности планеты)
T₁²/T₂²= R₁³/R₂³	Закон Кеплера для периодов обращение T1 и T2 двух тел, вращающихся вокруг одного притягивающего центра на расстояниях R1 и R2 соответственно
Р=m(g+a) Р=m(g-a)	Вес тела, движущегося с ускорением а↑ Вес тела, движущегося с ускорением а↓
Термодинамика
Q=cm(T₂-T₁) C=cm Q=C(T₂-T₁)	Количество теплоты (энергии) необходимое на нагревания некоторого тела (C-теплоемкость, c-удельная теплоемкость, m- масса, t- температура)
Q=λm	Количество теплоты при плавлении (λ – удельная теплота плавления, m – масса расплавившегося тела или кристаллизовавшейся жидкости)
Q=rm	Количество теплоты при парообразовании (r – удельная теплота парообразования, m – масса испарившейся жидкости или конденсировавшегося пара)
Q=qm	Количество теплоты при сгорании топлива (q – удельная теплота сгорания топлива, m – масса сгоревшего топлива)
A=P∙ΔV = m/M∙ R∙ΔT, p = const	Работа идеального газа
U=3/2∙M/µ∙RT	Внутренняя энергия идеального одноатомного газа
ΔU=A+Q	Первый закон (начало) термодинамики (ЗСЭ) (Q – теплота полученная (отданная) газом)
η= (Q₁— Q₂)/ Q₁	КПД тепловых двигателей
η= (Т₁— Т₂)/ Т₁	КПД идеальных двигателей (цикл Карно)
ρ=pM/RT	Абсолютная влажность (ρ — абсолютная влажность, р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура)
φ=ρ/ρ₀∙100% φ=P/P₀∙100%	Относительная влажность (ρ — абсолютная влажность, ρ₀ -количество водяного пара, которое необходимо для насыщения 1 м3 воздуха при данной температуре) (P — давление водяного пара, Pо — давление насыщенного пара при данной температуре)
E_p = σS	Поверхностное натяжение (σ – коэффициент поверхностного натяжения данной жидкости)
F_н= σL	Сила поверхностного натяжения, действующая на участок границы жидкости длиной L
Статика и Гидростатика
M=F∙ℓ	Момент силы (F – сила, ℓ – плечо силы, т.е. кратчайшее расстояние между точкой опоры, относительно которой происходит вращение и линией действия силы)
Р=F/S	Давление (F – сила, S – площадь на которую распределено действие силы)
P=ρ∙g∙h P=P₀+ρ∙g∙h	Давление на глубине жидкости (p0 – атмосферное давление, ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости)
Fa=ρ_ж∙g∙V	Закон (сила) Архимеда (V – объем погруженной части тела, который иногда также называют объемом вытесненной жидкости)
Электростатика
q = Ne	Электрический заряд (N – количество элементарных зарядов, е – элементарный заряд)
λ=q/L, σ=q/S, ρ=q/V	Линейная, поверхностная и объемная плотность заряда
F=k∙q₁∙q₂/R²F=k∙q₁∙q₂/εr²	Закон Кулона (сила электростатического взаимодействия двух зарядов величиной q1 и q2, находящихся на расстоянии r друг от друга в веществе с диэлектрической проницаемостью ε):
E=1/(4πεε₀)	Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра
E= σ/(2εε₀)	Напряженность электрического поля, которую создает заряженная плоскость
ε=E₀/E	Диэлектрическая проницаемость
E=F/q	Напряженность электрического поля
E=k∙q/R²	Напряженность электрического поля точечного заряда
E=2πkσ	Напряженность электрического поля бесконечной плоскости
W= k∙q₁q₂/R = k∙q₁q₂/εr	Потенциальная энергия взаимодействия двух электрических зарядов
U=Ed, Δφ=E∙ Δl	Cвязь между напряженностью поля и напряжением
A=qU, U=A/q	Работа электрического поля, Напряжение
A= qEd, U=E∙d	Работа электрического поля в однородном поле при перемещении заряда вдоль его силовых линий, Напряжение для однородного электрического поля
φ=W/q	Потенциал
φ=k∙q/R	Потенциал точечного заряда
C=q/U	Электроемкость
C=S∙ε∙ε₀/d	Электроемкость плоского конденсатора
q=CU	Заряд конденсатора
E = U/d = σ/εε₀	Напряженность поля внутри конденсатора
F=qE/2	Сила притяжения пластин конденсатора
W=qU/2=q²/2С=CU²/2	Энергия заряженного конденсатора
Электрический ток
I=q/t	Сила тока (q – заряд, протекший через некоторое поперечное сечение проводника за время t)
R=ρ∙ℓ/S	Сопротивление проводника (l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника)
R=R₀(1+αt)	Сопротивление проводника
I=U/R	Закон Ома для участка цепи (U – электрическое напряжение)
I₁=I₂=I, U₁+U₂=U, R₁+R₂=R	Законы последовательного соединения
U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R	Законы параллельного соединения
ε=A_ст/q	Электродвижущая сила источника тока, ЭДС (Aст – работа сторонних сил по перемещению заряда q)
I=ε/(R+r)	Закон Ома для полной цепи
I=ε/r	Сила тока короткого замыкания (R=0)
Q=A=I²Rt	Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока, протекающего по проводнику, обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике
P=IU=U²/R=I²R	Мощность электрического тока
m = kQ = kIt	Электролиз. Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит
Магнетизм
Fa=IBℓsinα	Сила Ампера (В – индукция магнитного поля, I – сила тока в проводнике, l – его длина, α – угол между направлением силы тока (т.е. самим проводником) и вектором индукции магнитного поля)
M = NBIS∙sinα	Момент сил, действующих на рамку с током (N – количество витков, S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции)
Fл=Bqυ∙sinα	Сила Лоренца (q – электрический заряд частицы, υ – её скорость, α – угол между направлением движения частицы и вектором индукции магнитного поля)
R=mU/qB	Радиус траектории полета заряженной частицы в магнитном поле
B=Fmax/ℓ∙I	Вектор магнитной индукции
Ф=BSсos α Ф=LI	Магнитный поток Φ через площадь S
Ei=ΔФ/Δt	Закон электромагнитной индукции
Ei=Вℓυsinα	ЭДС индукции при движении проводника
Esi=-L∙ΔI/Δt	ЭДС самоиндукции
Wм=LI²/2	Энергия магнитного поля катушки
Колебания
a+ω₀²x=0	Уравнение описывает физические системы способные совершать гармонические колебания с циклической частотой ω0
x = A cos (ωt + φ0)	Уравнением движения для гармонических колебаний (x– координата тела в некоторый момент времени t, A – амплитуда колебаний, ω – циклическая частота колебаний, φ0 –начальная фаза колебаний).
Х=Хmax∙cos ωt	Уравнение гармонических колебаний
T=t/N, v=N/t=1/T ω=2πv=2π/T	Связь некоторых характеристик колебательного процесса (T – период, N – количество полных колебаний, v – частота колебаний, ω – циклическая частота)
υ = x'(t) = –Aω sin (ωt + φ0)	Скорость тела при колебательном движении
υ_m = ωA	Максимальное (амплитудное) значение скорости
a = υ'(t) = x»(t) a = –Aω² cos (ωt + φ0)	Ускорение тела при колебательном движении
a_m = Aω²	Максимальное (амплитудное) значение ускорения
ω₀=√(g/ℓ) T=2π√ℓ/g	Циклическая частота и период колебаний математического маятника (l – длина маятника, g – ускорение свободного падения)
ω₀=√(k/m) T=2 π √m/k	Циклическая частота и период колебаний пружинного маятника (m – масса груза, k – коэффициент жесткости пружины маятника)
W=CU²/2+LI²/2 W=CU_max²/2=LI_max²/2	Электрический контур
T=2π ∙√LC ω=2π/T=1/(√LC)	Период колебаний кол. контура и циклическая частота
I_д=I₀/√2, I_д=I_max/√2 U_д=U₀/√2, U_д=U_max/√2	Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин; Действующее значение силы тока и напряжения
P=U_дI_д=I_д²R=U_д²/R	Мощность в цепи переменного тока
U₁/U₂=n₁/n₂	Трансформатор: если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2
λ= υТ=υ/v	Волны. Длина волны (υ – скорость распространения волны, T – период, v – частота)
X_L=ωL=2πLν	Индуктивное сопротивление
Xc=1/ωC	Емкостное сопротивление
Z=√(Xc-X_L)²+R²	Полное сопротивление
Оптика
L_опт=L_n	Оптическая длина пути (L – геометрическая длина траектории, по которой «идет» луч света, n – показатель преломление среды, в которой это происходит)
x=mλL/d	Интерференционная схема Юнга (L – расстояние между экраном и плоскостью в которой расположены две щели, d – расстояние между этими щелями, λ – длина волны света, которым освещаются щели).
d∙sin φ=k λ	Формула дифракционной решетки (d – период решетки, или расстояние между соседними штрихами, φ – угол под которым наблюдается очередной дифракционный максимум, k – номер (порядок) максимума, λ – длина волны света, падающего на дифракционную решетку)
n₂₁=n₂/n₁= υ₁/ υ₂	Закон преломления света на границе двух прозрачных сред (α – угол падения, β – угол преломления, n1 – показатель преломления первой среды, из которой падает луч, n2 – показатель преломления второй среды, в которую проникает луч)
n₂₁=sinα/sinβ	Показатель преломления
1/F=1/d + 1/f	Формула линзы (d – расстояние от линзы до предмета, f – расстояние от линзы до изображения, F – фокусное расстояние, D – оптическая сила линзы)
D=1/F	Оптическая сила линзы
Δd=kλ, Δd=(2k+1)λ/2	max интерференции, min интерференции
Атомная и ядерная физика
E=hv=hc/λ	Энергия кванта света, т.е. фотона (h – постоянная Планка, λ – длина волны света, v – частота света)
P=mc=h/ λ=Е/с	Импульс фотона
hν=A_вых+(mU²/2)_max hν=A_вых+Ek, Ek=еU_зhν_min=A_вых=hc/λ	Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ) (А_вых – работа выхода, слагаемое в скобках –максимальная кинетическая энергия вылетающих электронов, v – частота падающего света)
(mU²/2)_max=еU_з	Максимальная кинетическая энергия вылетающих электронов
ν_к = A_вых/h	Красная граница фотоэффекта
hν_nm = \|En – Em\|	Второй постулат Бора (правило частот). При переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний
N=N₀∙2^—^t^/^T	Закон радиоактивного распада
E_CB=(Zm_p+Nm_n-Mя)∙c²	Энергия связи атомных ядер
Основы СТО
ℓ=ℓ₀∙√1-υ²/c²	Релятивистское сокращение длины. Длина тела, движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины
t=t₁/√(1-υ²/c²)	Релятивистское удлинение времени события. Время, за которое происходит некоторое событие в движущейся системе отсчета с точки зрения наблюдателя из неподвижной системы отсчета
υ=(υ₁+υ₂)/1+ υ₁∙υ₂/c²	Релятивистский закон сложения скоростей
Е = mс²	Связь энергии и массы тела. Наименьшей энергией Е0 тело обладает в инерциальной системе отсчета относительно которой оно покоится и называется собственной энергией тела (энергия покоя тела)

Источник

Одинаковое расстояние можно проехать за разное время.

Например, спортивная машина один километр может проехать быстрее, чем тяжело нагруженная грузовая машина. Одна и та же машина может ехать как быстрее, так и медленнее.

Обрати внимание!

Чтобы сравнить различные движения, необходимо знать скорость движения.

Скоростью движения называется величина, численно равная пути, проходимому телом в единицу времени.

Скорость вычисляется по формуле

v=st

, где

(s) — пройденный путь;

(t) — время.

Чем больше скорость, тем больший путь проходит тело за единицу времени. Если путь измеряется в метрах (м), а время движения в секундах (с), то скорость тела измеряется в (м/с).

Метр в секунду (м/с) — единица скорости в международной системе единиц.

Скорость можно выражать и в других единицах, например в км/с или в км/ч.
Различные примеры скорости:

1. скорость реактивного самолета — 3000 км/ч.

2. Скорость спринтера на дистанции — 37 км/ч.

3. Скорость звука в воздухе — 1224 км/ч.

4. Средняя скорость ходьбы — 6 км/ч.

5. Максимальная скорость гепарда — 114 км/ч.

6. Скорость улитки — 0,02 км/ч.

Источник

Формулы скорости, времени, расстояния?

Как выразить эти понятия друг одно через другие?

Анонимный вопрос

2 ноября 2018 · 236,8 K

Если вам известна скорость v и время t, то вы сможете найти расстояние S по формуле S=vt.

Обратите внимание на единицы измерения! Если вам дана скорость в километрах в час, то и время должно быть выражено в часах (или в метрах в секунду и секундах соответственно).

Выразить скорость из этой формулы можно следующим образом: v=S/t

А если вы хотите посчитать время, то воспользуйтесь формулой t=S/v

204,1 K