Калькулятор позволяет определить скорость природного газа в трубе согласно ГОСТ Р 55472-2019 «Системы газораспределительные. Сети газораспределения природного газа. Часть 0. Общие положения».
Общие данные.
При расчете пропускной способности надземных газопроводов учитывают максимально допустимый уровень шума, создаваемого движением газа, по ГОСТ 12.1.003-2014 «Система стандартов безопасности труда. Шум. Общие требования безопасности».
Скорость движения газа рассчитывается по формуле п.7.1.6. ГОСТ Р 55472-2019 «Системы газораспределительные. Сети газораспределения природного газа. Часть 0. Общие положения». Формула учитывает коэффициент сжимаемости газа, температуру и давление газа. Формула составлена на базе уравнения идеального газа.
Коэффициент сжимаемости в случае необходимости определяется в соответствии с:
- ГОСТ 30319.2-2015 «Газ природный. Методы расчета физических свойств. Вычисление физических свойств на основе данных о плотности при стандартных условиях и содержании азота и диоксида углерода»;
- ГОСТ 30319.3-2015 «Газ природный. Методы расчета физических свойств. Вычисление физических свойств на основе данных о компонентном составе».
При этом следует учесть, что для газопроводов с давление газа до 1,2 МПа коэффициент сжимаемости лежит в пределах от 0,98÷1,0, поэтому в методике гидравлического расчета он не учитывается. В данном расчете по умолчанию принят коэффициент равный Z=1. Калькулятор позволяется менять значение коэффициента.
ГОСТ Р 55472-2019 предусматривает расчет абсолютного давления газа по формуле: Pa=Pи+0.1012. Калькулятор рассчитывает абсолютное давление газа по классической формуле: Pa=Pи+0.101325.
Действующими НТД (ГОСТ Р 55472-2019, СП 42-101-2003) скорость движения газа рекомендуется принимать для газопроводов:
-
- низкого давления — не более 7 м/с;
- среднего давления — не более 15 м/с;
- высокого давления — не более 25 м/с.
Заданные скорости газа в трубе не являются основным критериям для выбора диаметра газопровода. Диаметры газопроводов определяются в ходе полного гидравлического расчета систем газораспределения и газопотребления.
Примечание.
В комментарии приветствуются пожелания, замечания и рекомендации по улучшению программы.
Поделиться ссылкой:
Помощник ГИП

Группа: Друзья
Репутация: 12
Город: Donetsk
Замечания: 0%
Статус: Оффлайн
Quote (Abit)
Тогда не прибегая ко второму варианту как иначе перевести объём НМ3 (норм.метр3) в М3?
физический объем газа определяется по формуле: Qm = Qb / C , м.куб/ч
где
С = (Р х Тb) / (Рb х Т х Z) – коэффициент коррекции;
Qm – физический объем
Qb – объем в нормальных условиях
Р – абсолютное давление газа в рабочих условиях;
Рb – абсолютное давление газа в нормальных условиях (Рb=0,101325 МПа);
Z – коэффициент сжимаемости в рабочих условиях.
Т – температура газа в рабочих условиях;
Тb – температура газа в стандартных условиях (Тb= 293,15 (273,15+20) К)
Пример
Объем в нормальных условиях( часовой расход газа):
Зима: максимальный 160 н. м.куб/ч
Минимальный (50% нагрузки) 80 н.м.куб/ч
Переходный период : максимальный 80 н.м.куб/ч
минимальный (50% нагрузки) 40 н.м.куб/ч
Давлении газа – Рмах =0,08 МПа ( 0,8 кгс/см.кв), Рмin = 0,02 Мпа (0,2 кгс/см.кв), согласно ТУ
Зима: Рмах С = (0,101325+0,08) х 293,15 / 0,101325 х (273,15+5) х 0,994 = 1,89
Рмin С = (0,101325 + 0,02) х 293,15 / 0,101325 х( 273,15+5) х 0,9976 = 1,26
Переходный:
Рмах С= (0,101325 + 0,08) х 293,15 / 0,101325 х (273,15+8) х 0,995 = 1,87
Рмin С =( 0,101325+ 0,02) х 293,15 / 0,101325 х (273+8) х 0,997 = 1,05
Физический объем составит:
Зима:
При Рмах Qmах = 160/ 1,89 = 84,65 м.куб/ч
Qmin = 80/1,89 = 42,3 м.куб/ч
При Рмin Qmах = 160/ 1,,26 = 126,98 м.куб/ч
Qmin = 80/1,26 = 63,49 м.куб/ч
Переходный период:
При Рмах Qmах = 80/1,87 = 42,78 м.куб/ч
Qmin = 40/1,87 = 21,39 м.куб/ч
При Рмin Qmах = 80/1,05 =76,19 м.куб/ч
Qmin = 40/1,05 = 38,09 м.куб/ч
Коэфф сжимаемости можно найти в спавочниках
Далее уже используя полученные значения находите скорость по площади сечения трубы
Сообщение отредактировал StaG – Четверг, 26.03.2009, 14:07
Unit Converter
Enter the volume flow rate and the diameter of the natural gas pipe into the calculator to determine the natural gas velocity.
- All Velocity Calculators
- Stream Velocity Calculator
- Flow to Velocity Calculator
- Gas Piping Size Calculator
Natural Gas Velocity Formula
The following equation is used to calculate the Natural Gas Velocity.
NGV = Q / (pi*D^2/4)
- Where NGV is the Natural Gas to Velocity (m/s)
- Q is the volumetric flow rate (m^3/s)
- D is the internal diameter of the natural gas pipe (m)
What is a Natural Gas Velocity?
Definition:
A natural gas velocity is a measure of the linear rate of speed of natural gas moving through a pipe.
How to Calculate Natural Gas Velocity?
Example Problem:
The following example outlines the steps and information needed to calculate the Natural Gas Velocity.
First, determine the volumetric flow rate. In this example, the flow is found to be 600 m^3/s.
Next, determine the internal diameter of the natural gas pipe. For this problem, the internal diameter of the natural gas pipe is found to be 1.2m.
Finally, calculate the Natural Gas Velocity using the formula above:
NGV = Q / (pi*D^2/4)
NGV = 600 / (3.14159*1.2^2/4)
NGV = 530.31 m/s

|
р3 = 840 9,8 ( |
105 |
−3 |
− |
0,012 |
( 0,0268 |
43,62 |
+ 2,93 ) = 65300 Па |
||
|
840 9 |
,8 |
( 7,85 10−3 )2 2 9,8 |
0,1 |
||||||
Давление насыщенного пара равно 2 кПа. Так как 65,3 >> 2, то сифон будет работать.
При решении задач на расчет газопроводов нужно учитывать, что плотность совершенного10 газа зависит от давления и температуры: ρ=p / RT
Это уравнение состояния газа (уравнение Клайперона). Здесь R – газовая постоянная, равная для воздуха 287дж/кг°К.
В разных сечениях трубопроводной системы давление может отличаться на десятки атмосфер. Это приводит к существенному различию плотностей в сечениях газового потока и, как следствие, к различию объёмных расходов.
При движении газа в сечениях потока сохраняется массовый расход!
Qm = ρ1 ϑ1 ω1=ρ2 ϑ2 ω2=……=ρi ϑi ωi=const (49)
Как известно, капельная жидкость в сечении обладает потенциальной
и кинетической энергией.
Газы обладают потенциальной, кинетической и внутренней энергией.
Внутренняя энергия газа зависит от температуры и вида процесса, по которому измененяется его состояние.
Если при движении газа по трубам вследствие теплообмена с окружающей средой температура по длине не изменяется, то имеет место изотермический процесс (T=const). При этом внутренняя энергия в сечениях трубопровода остается постоянной. Уравнение Бернулли при изотермическом течении газа имеет такой же вид, как и для несжимаемой жидкости, за исключением того, что в сечениях потока разная плотность:
|
p |
α ϑ |
2 |
p |
2 |
α ϑ |
2 |
||||||
|
z + |
1 |
+ |
1 1 |
= z |
2 |
+ |
+ |
2 2 |
+ h |
. (50) |
||
|
1 |
ρ1 |
g |
2g |
ρ2 g |
2g |
1−2 |
||||||
10 Газ называется совершенным, если его давление, плотность и абсолютная температура удовлетворяют уравнению Клапейрона и удельную внутреннюю энергию газа можно опре-
делить в виде: U=cv T
-83-
Основные задачи при расчете газопроводов
1.Определить расход газа, если известны давления в начале и конце газопровода.
2.Определить давление в сечении газопровода, если известен расход газа
идавление в каком –нибудь другом сечении.
3.Определить диаметр газопровода, если известны давления в начале и конце газопровода и расход.
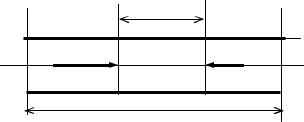
Для решения этих задач получим зависимость между массовым расходом газа и давлениями в сечениях 1-1 и 2-2 (Рис. 22 ).
5.7.1. ВЫВОД РАСЧЕТНЫХ ЗАВИСИМОСТЕЙ ДЛЯ ИЗОТЕРМИЧЕСКОГО ТЕЧЕНИЯ
При движении газа в трубопроводе постоянного диаметра одновременно изменяются давление, плотность и скорость движения. Так, давление уменьшается из-за необходимости совершать работу по преодолению силы трения, плотность также уменьшается (при изотермическом течении она пропорциональна давлению). Средняя скорость движения газа увеличивается по ходу его движения, так как массовый расход остается постоянным, а плотность падает. Таким образом, использовать в явном виде уравнение Бернулли (50) для расчета нельзя.
Применим уравнение (50) к элементу газопровода длиной dl, на котором можно считать постоянными скорость и плотность газа.
1 dl 2
р p+dp
p+dp
|
1 |
2 |
|
|
Рис. 22 |
L |
|
|
Схема к выводу расчетных зависимостей при движении газа |
||
|
Уравнение Бернулли для выделенного элемента: |
||
|
р/ρg = (p+dp)/ρg + dhдл |
(51) |
-84-

|
−dp = ρ g dh = ρ λ |
dl |
ϑ2 |
|
|
дл |
d |
2 |
|
Потери на трение определяются по тем же формулам, что и для несжимаемой жидкости. Коэффициент трения λ=f(Re, э/d).
Докажем, что при изотермическом течении, когда постоянна вязкость, по длине трубы число Re не изменяется.
Re = ϑ ηd ρ = π4 Qd ηρ = π4 dQmη = const
Следовательно, коэффициент трения также постоянен по длине трубопровода.
Выразим в уравнении (51) скорость и плотность через параметры в начальном сечении и массовый расход.
ρ ϑ2=ρ Qm2/ ρss2 = Qm2/ s2 = Qm2 p1/ ρ1 p s2.
Здесь учтено, что по уравнению состояния
|
−dp = ρ λ |
dl |
ϑ2 |
= λ |
dl |
|||
|
d |
2 |
d |
|||||
p/ ρ = p1/ ρ1 =RT=const.
Qm2 p1
2 ρ1 p s2
Разделяем переменные, учитываем, что s =π d2/4, интегрируем и получаем следующие расчетные формулы:
Определение давления при известном расходе
|
2 |
2 |
L |
Q |
2 |
p |
16 |
||||||
|
p |
− p |
2 |
= λ |
m |
1 |
; |
(52) |
|||||
|
1 |
d 5 |
ρ1 π 2 |
||||||||||
|
Определение массового расхода при известных давлениях р1 и р2 |
|
Qm = |
( p 2 |
− |
p 2 |
) ρ |
1 |
π 2 |
d 5 |
||
|
1 |
2 |
; |
(53) |
||||||
|
L λ p1 16 |
|||||||||
|
Коэффициент трения определяется по тем же формулам, что и для нью- |
|||||||||
|
тоновской жидкости: |
|||||||||
|
λ=64/Re |
– ламинарный режим |
||||||||
|
λ=0,11(68/Re+ |
э/d)0,25 |
– турбулентный режим |
Так как коэффициент трения λ зависит от числа Rе и, следовательно, от расхода, при определении массового расхода по формуле (53) сначала нужно
-85-

задаться величиной λ (например, λ=0,02), определить расход в первом приближении, и затем уточнить значение λ и Qm. Как это делается, проиллюстрировано на примере расчета.
5.7.2. ПРИМЕР РАСЧЕТА
Воздух при t=2°C движется по трубопроводу диаметром d=0,1м и длиной 15км. Давление в начале трубопровода 4,41Мпа, а в конце 0,29 Мпа. Определить массовый расход. Трубопровод изготовлен из новых стальных сварных труб.
Решение задачи.
Используем формулу (53).
Здесь неизвестны плотность газа в начале трубопровода ρ1 и коэффициент трения.
• Определяем плотность газа в начале трубопровода.
ρ1 =р1/RT =4,41 106/287/275=56,6кг/м3.
Здесь R=287 – газовая постоянная для воздуха, T=273+2=275 –абсолютная температура.
• Предполагаем турбулентный режим движения, задаемся величиной λ =0,02 и вычисляем в первом приближении массовый расход:
|
Qm = |
( 4,412 −0,292 )1012 56,6 π 2 0,15 |
=1,04кг / с; |
|
15000 0,02 4,41 106 16 |
• Определяем число Re и режим движения газа.
|
Re = |
ϑ d ρ |
= |
4 Q ρ = |
4 Qm |
= |
4 1,04 |
= 7,5 105 ; |
|
|
η |
π 0,1 17,6 10−6 |
|||||||
|
π d η π d η |
Коэффициент динамической вязкости определяем с помощью Приложе-
ния 3.
При р=98кПа и t=2°C – ν=13,9 10-6м2/с, плотность ρ=1,27кг/м3, следовательно:
η = ν ρ = 13,9 10-6 1,27 = 17,6 10-6 Па с.
-86-

• Уточняем значение коэффициента трения. При турбулентном режиме:
λ=0,11(68/Re+ э/d)0,25 = 0,11(68/7,5 105 +0,1 10-3/0,1)0,25 = 0.0199=0,02.
Для новых стальных сварных труб э =0,1мм.
Таким образом, значение коэффициента трения практически не изменилось и массовый расход газа определен правильно.
5.8. ОПРЕДЕЛЕНИЕ СКОРОСТИ И РАСХОДА ПРИ ИСТЕЧЕНИИ
ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
На практике жидкость может вытекать из ёмкостей через отверстия и насадки различных типов.
|
рм |
|||
|
Q |
H1 |
||
|
отверстие |
|||
|
d1 |
|||
|
избыточное |
Насадки |
применяются |
|
|
для увеличения расхода |
|||
|
давление газа |
|||
|
жидкости! |
|||
|
рх =? |
|||
|
H2 |
|
внешний цилин- |
d2 |
сжатое сечение струи |
|
|
дрический |
наса- |
||
|
док |
d2 |
область, заполненная |
|
|
вращающимися вихрями |
Рис.23 Схема истечения через отверстие и насадок
Боковые частицы (пунктирные стрелки) по инерции движутся горизонтально и сжимаот ядро струи. На некотором расстоянии от входа в отверстие
|
(насадок) получается сжатое сечение. |
|
|
sс / s = ε – коэффициент сжатия. |
ε = 0,64 при Re > 104. |
-87-

В сжатом сечение струи в насадке давление меньше, чем атмосферное рат. Жидкость движется в сторону большего давления. Частицы жидкости с малой скоростью (у стенки) поворачивают обратно. Образуются вихри.
При уменьшении давления в сжатом сечении увеличивается скорость движения, следовательно, и расход. Если бы не было насадка (отверстие), давление в струе равно атмосферному, скорость меньше и расход меньше.
Основы теории процесса истечения
При решении задач на истечение жидкости применяются следующие за-
коны:
• закон сохранения расхода: Q = сonst в любом сечении потока.
Для схемы Рис.23 расход через отверстие равен расходу через насадок и равен тому расходу, который поступает в бак.
•закон сохранения энергии: разность потенциальных энергий на входе и выходе из отверстия (насадка) превращается с некоторыми потерями в кинетическую энергию вытекающей струи жидкости.
Потенциальная энергия жидкости равна m g z +m p/ρ. Поскольку высота отверстия (насадка) незначительна, z≈const и разность потенциальных энергий на входе и выходе из отверстия (насадка) равна:
Eпот = m pвх/ρ – m pвых/ρ = m ( pвх – рвых)/ρ
Кинетическая энергия струи равна mϑ2/2. Закон сохранения энергии:
ϕ m ( pвх – рвых)/ρ = mϑ2/2.
Здесь ϕ< 1 – «к.п.д.» процесса, он учитывает, что не вся потенциальная энергия превращается в кинетическую, часть её расходуется на преодоление гидравлических сопротивлений и переходит в тепло.
|
ϑ =ϕ |
2( рвх − рвых ) |
(54) |
|
|
ρ |
|||
Формула (54) определяет скорость в сжатом сечении струи для отверстия и выходную скорость для насадка.
При истечении через отверстие имееют место потери на входе, а при истечении через насадок – те же потери на входе плюс потери на вихреобразование внутри насадка.
-88-
Проводимость канала определяет его способность транспортировать газ. Она выражается в единицах объема газа, проходящего через данное сечение в единицу времени. Зависимости для расчета проводимости элемента, работающего в различных условиях, являются весьма сложными и зависят от режима течения, а также от геометрических параметров канала и свойств его поверхности. Расчеты проводимости и потока газа при турбулентном режиме течения трудно трактовать аналитически. Количественное определение параметров вязкостного потока также представляет трудности, поскольку зависит не только от формы канала, но и от давления газа. Однако при тех диапазонах давлений, которые имеют место в условиях высокого вакуума, поток является молекулярным, а не вязкостным.
Уравнения для расчета параметров вязкостного потока
В общем случае уравнения для расчета проводимости и потока газа при вязкостном режиме течения получены для трубопроводов и каналов, имеющих сечение простой геометрической формы – круглое или прямоугольное. Эти выражения используются, например, для расчета времени, необходимого для откачки сосуда через трубопровод, имеющий круглое или прямоугольное поперечное сечение.
Течение в трубопроводах круглого сечения
Поток газа по прямому трубопроводу круглого сечения в условиях вязкостного режима определяется уравнением Пуазейля:
$$frac{Q}{P_{1}-P_{2}}=K frac{d^{4}P}{eta L}, (60)$$
где d – диаметр трубы; L – длина трубопровода; η – динамическая вязкость газа; р – среднее давление в трубопроводе; р1 и р2 – давления на противоположных концах трубы.
Для сухого воздуха при 20 °С данное уравнение приобретает вид:
$$Q= frac{750d^{4}bar{P}}{L}(P_{1}-P_{2}), (61)$$
где Q – поток газа, Торр – л/с; d – диаметр трубопровода, см; L – длина трубопровода, см; р – это давление, Торр.
Проводимость круглого трубопровода, л/с, для воздуха при 20 °С приведено ниже:
$$C= frac{2,94pd^{4}}{L}, (62)$$
Течение в прямоугольных каналах
Уравнение Пуазейля для потока воздуха при 20 °С, текущего по прямоугольному каналу с большей стороной сечения а и меньшей b, имеет следующий вид, л/с:
$$C= frac{30a2b2KP}{L}, (63)$$
где К — это коэффициент формы, значение которого зависит от b/а.
Как можно видеть, проводимость прямоугольной диафрагмы (отверстия) быстро увеличивается при переходе сечения от прямоугольной щели к квадрату.
Так же, как и в случае круглого трубопровода, выражение для С позволяет получить соотношение для объемного потока газа в зависимости от перепада давлений в канале.
$$C= frac{pK}{Delta p}, (64)$$
где
$$F= frac{Cp}{Delta p}, (64)$$
Таким образом,
$$K= frac{30a_{2}b_{2}K}{L} cdot Delta p, (65)$$
л/с.
Уравнения для расчета параметров молекулярного потока
При низких значениях давления межмолекулярные столкновения происходят реже, чем столкновения со стенкой, поэтому последние определяют параметры газового потока по каналу. Проводимость канала в условиях молекулярного потока зависит от двух факторов:
- Скорости, с которой молекулы поступают в канал.
- Вероятности прохождения молекул по системе.
Первый фактор зависит от площади сечения входа в систему, а последний определяется последующей серией столкновений со стенками, в результате которых молекула в конечном итоге перемещается по каналу или отбрасывается обратно в откачиваемый сосуд.
Рассмотрим вначале случай очень тонкой диафрагмы в пластине. В данном случае для определения проводимости диафрагмы нас интересует ее площадь А, а не свойства стенок канала. Объем газа, проходящего через диафрагму – ее проводимость – составляет:
$$C_{a}= frac{1}{4}AV=(frac{2}{p})^{-1} – V^{0}A, (66)$$
если молекулы имеют распределение скоростей по Максвеллу. Значения проводимости зависят от молекулярной массы и кинетической энергии. Случай, когда столкновения молекул со стенками трубопровода являются более важными, чем проводимость отверстия, рассмотрен ниже.
Формула Кнутсена
Проводимость СΥотрезка длинной трубы длиной L с переменной площадью сечения А и периметром Н была рассчитана Кнудсеном и составляет:
$$C_{Upsilon} = frac{4}{3} sqrt{ frac{H( delta)}{A^{2} L} cdot de }. (67)$$
Были приняты следующие допущения:
- Длина трубопровода значительно больше диаметра.
- Направление движения отскочивших молекул после столкновения со стенками не зависит от направления их движения до столкновения.
- Угловое распределение отскочивших молекул подчиняется закону косинуса.
Допущение 1 предполагает, что влияние отверстия является незначительным, а величина проводимости, получаемая из уравнения (67), относится к молекулам внутри трубы, удаленным от отверстия. Для получения приближенных выражений для проводимости всей трубы нужно включить последовательную проводимость отверстий. Карлсон приводит формулу для трубопровода с периметром Н, площадью Л и длиной L:
$$C_{a}=1+ frac{3}{16} cdot 9 frac{LH}{A}). (58)$$
Коэффициент Клаузинга
Проводимость длинного трубопровода связана с проводимостью входного отверстия коэффициентом [1 +3/16(LH/A)]-1 Ca. Этот коэффициент можно интерпретировать как вероятность случайного входа молекулы в отверстие и ее прохождения до самого конца трубопровода.
Целесообразно рассматривать проводимость с точки зрения проводимости отверстия и соответствующей вероятности прохождения молекулы (коэффициента Клаузинга), поэтому
$$C=CA cdot P_{1 to 2}= 1/4vA_{1}P_{1to 2}. (69)$$
Так как проводимость не зависит от направления движения молекул,
$$A_{1}P_{1 to 2} = A_{2} P_{1 to 2}. (70)$$
Примеры. Выражение для потока газа по длинному прямому трубопроводу было дано Кнудсеном:
$$Q= frac{ pi d^{3/2}}{L}$$
$$Q=( pi d^{3/2}/L)n_{a}(P_{1}-P_{2}), (71)$$
где d – диаметр трубопровода; L – длина трубопровода; nа – средняя скорость молекулы; р1 и р2 – давления на противоположных концах трубопровода.
Для сухого воздуха при 20 °С d и L, выраженных в дюймах, а р – в Торр, данное уравнение принимает следующий вид:
$$Q=(80d^{3}/L)n_{a}(p_{1}-p_{2}), (72)$$
Приблизительные значения некоторых вероятностей прохождения имеют точность в пределах + 10%. Это разнообразные методы, которые включают аналитические методы, расчеты по методу пробной частицы Монте-Карло и методу вариаций. Карлсон исследовал различные геометрические формы и ссылается на соответствующие источники. Примеры числовых расчетов можно найти в работе Карлсона.
