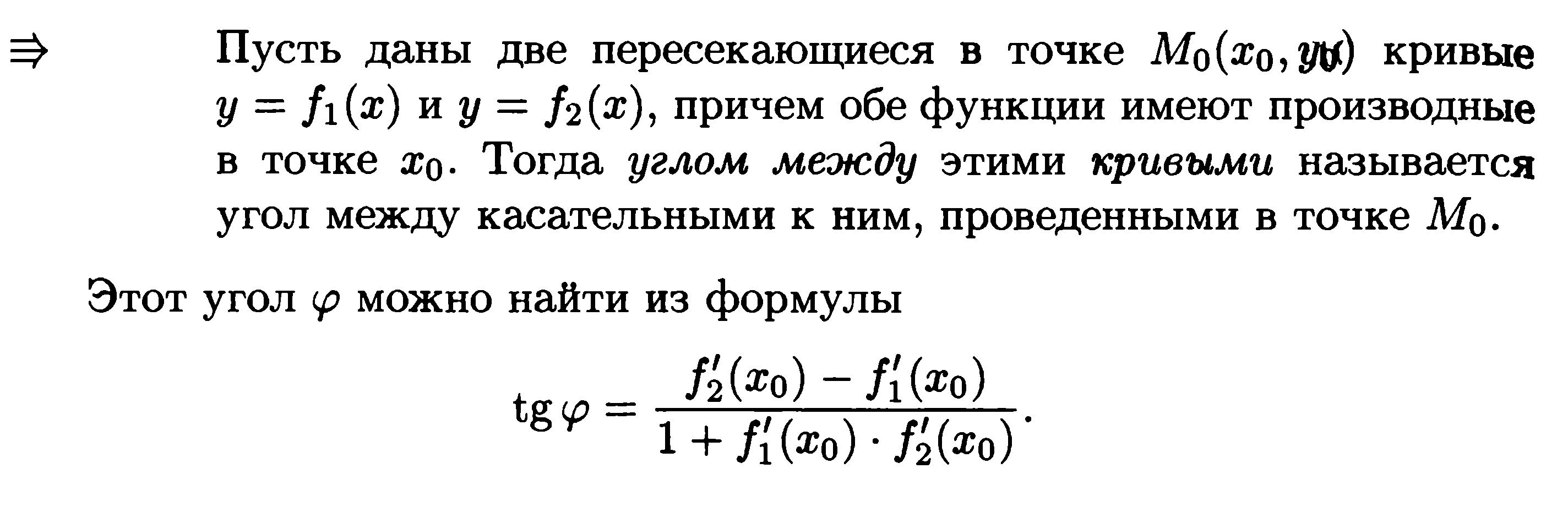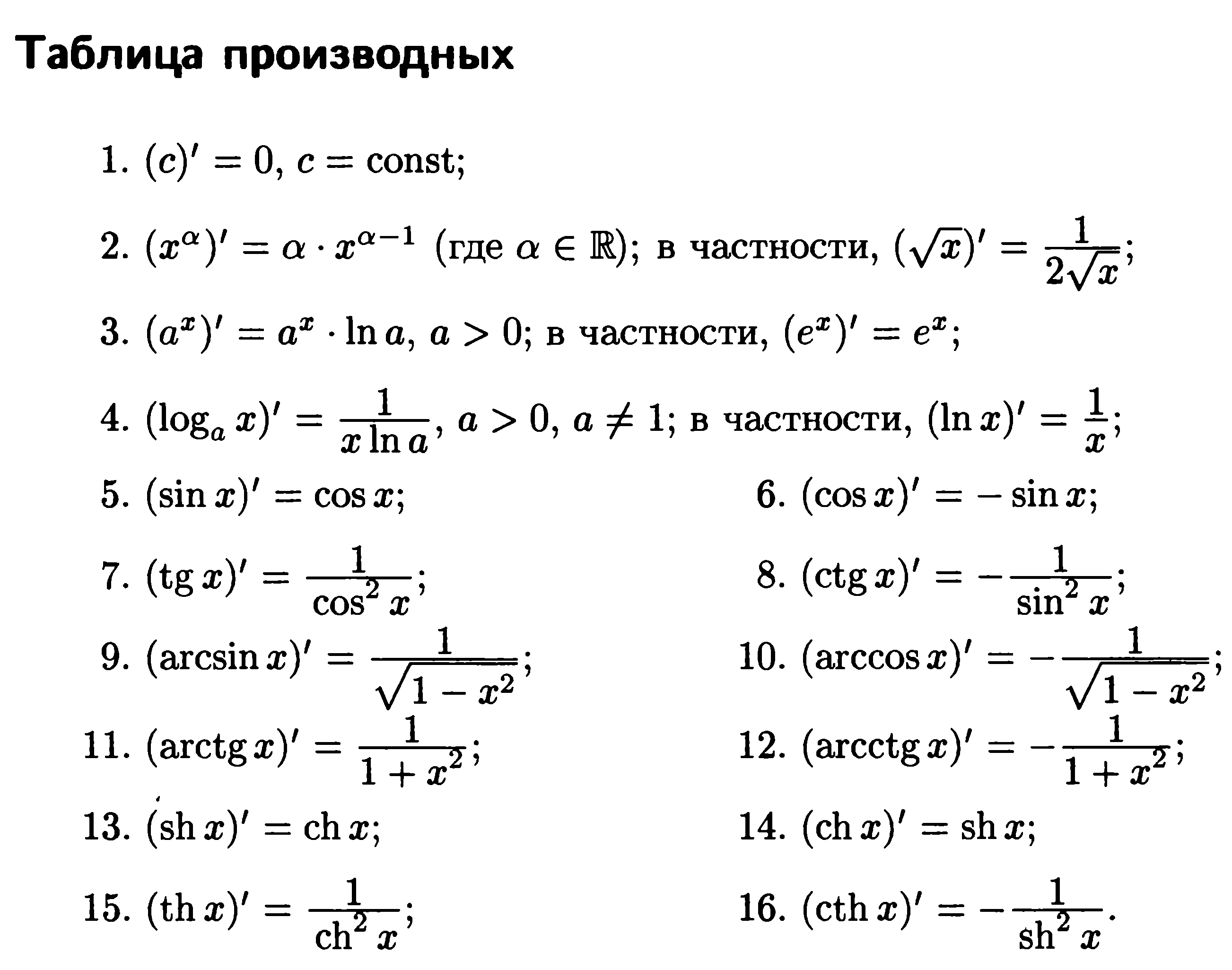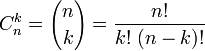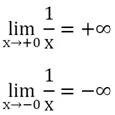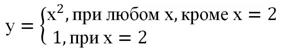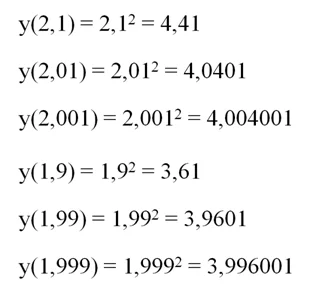1)
Скорость изменения функции
Пусть
s
= s(t) —
закон прямолинейного движения.
Тогда v(t0)
= s‘(t0)
выражает мгновенную
скорость
движения в момент времени t0.
Вторая производная a(t0)
= s”(t0)
выражает мгновенное
ускорение
в момент времени t0.
Вообще
производная функции y
= f(x)
в точке x0
выражает скорость изменения функции в
точке x0,
то есть скорость протекания процесса,
описанного зависимостью y
= f(x).
2
)
3
)
Производная сложной функции
Пусть
y –
сложная функция x,
т.е. y =
f(u),
u
= g(x),
или
(11)
Если
g(x)
и f(u)
– дифференцируемые функции своих
аргументов соответственно в точках x
и u =
g(x),
то сложная
функция (11) также дифференцируема в
точке x и
находится по формуле
(12)
Соотношение
(12) часто записывают в виде формулы
(13)
справедливой
при всех тех значениях x,
для которых
выполнены условия правила дифференцирования
сложной функции.
Замечание.
В случае сложной функции y
= f(u),
u = g(x)
аргумент u
функции
y называют
промежуточным аргументом в отличие от
независимой переменной x.
Тогда правило (13) можно сформулировать
так: производная сложной функции равна
произведению производной этой функции
по промежуточному аргументу u
на производную промежуточного аргумента
u
по независимой переменной x.
Для
сложной степенной функции
где
u
– дифференцируемая функция аргумента
x,
а n –
целое положительное число, формула (4)
производной степенной функции на
основании правила (13) примет вид
(14)

4
)
5)
6)
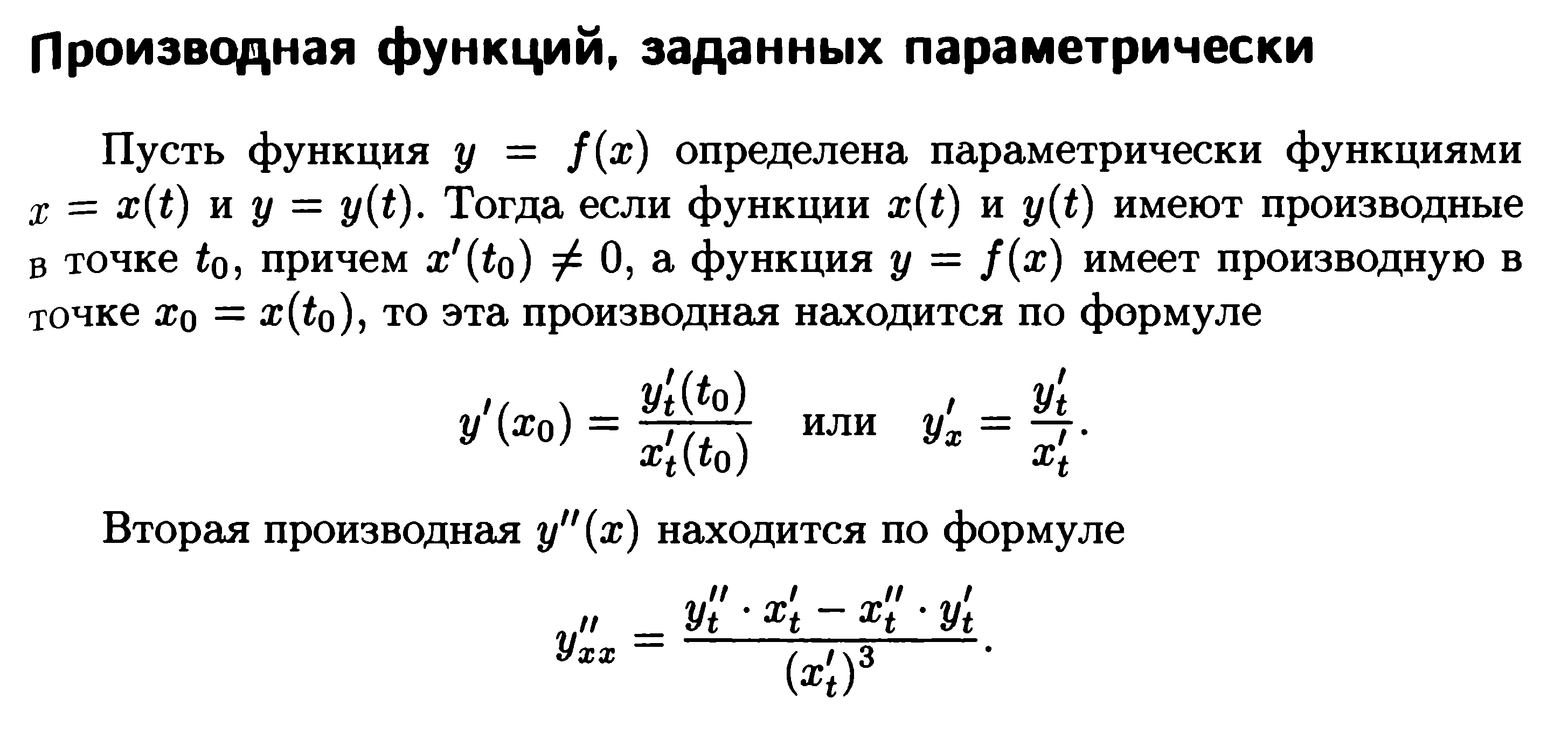
7)

P.S
: Разберите, для доказательства этой
теории любой пример из головы. Просто
решите.
8)Уравнение
касательной и нормали к графику функции
в точке
Уравнение
касательной
Пусть
функция задается уравнением y=f(x), нужно
написать уравнение касательной
в точке x0. Из
определения производной:
y/(x)=limΔx→0ΔxΔy
Δy=f(x+Δx)−f(x).
Уравнение
касательной
к графику
функции: y=kx+b (k,b=const). Из геометрического
смысла производной: f/(x0)=tgα=k
Т.к.
x0 и f(x0)∈
прямой, то уравнение касательной
записывается
в виде: y−f(x0)=f/(x0)(x−x0) , или
y=f/(x0)·x+f(x0)−f/(x0)·x0.
Уравнение
нормали
Нормаль—
это перпендикуляр к касательной
(см. рисунок).
Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к.
угол наклона нормали — это угол β1, то
имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка
(x0,f(x0))∈
нормали, уравнение примет вид:
y−f(x0)=−1f/(x0)(x−x0).
( ссыль.На нормальный
вид –
http://www.fizmatik.ru/index.php?option=com_content&view=article&id=19&Itemid=20)
9)

Формула
Лейбница для n-ой производной произведения
двух функций — обобщение правила
дифференцирования произведения двух
функций на случай n-кратного
дифференцирования.
Пусть
функции f и g — n раз дифференцируемые
функции, тогда
где
—
биномиальные коэффициенты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На этой странице вы узнаете
- Почему функции похожи на американские горки?
- Как с помощью производной оценить рост популярности видео в соцсети?
- Какие фокусы творят тригонометрия и геометрия вместе?
Она спешит на помощь быстрее, чем Чип и Дейл. Она наш спасательный круг в океане математики. Давайте посмотрим, как производная способна на такие чудеса.
Производная
Функции достаточно часто встречаются при решении задач. Они могут быть как составными частями какого-то задания, так и отдельным номером. Разумеется, встречаются не только простые функции. Если открыть банк заданий, то мы удивимся, насколько сложными они бывают. Так что делать с такими сложными и непонятными функциями?
Производная — одно из самых важных понятий математического анализа. С ее помощью можно описать поведение любой функции.
Предположим, мы хотим прокатиться на американских горках. Представим их вид сбоку: это череда подъемов и резких спусков. Мы можем с легкостью описать их: на каких участках будет подъем, а на каких спуск, насколько крутыми они будут, сколько раз вагончик преодолеет границу между подъемом и спуском или спуском или подъемом. Мы даже можем предположить, на каких участках вагончик разгоняется сильнее. Точно так же можно описать и любую функцию.
Представим наши американские горки в виде функции.
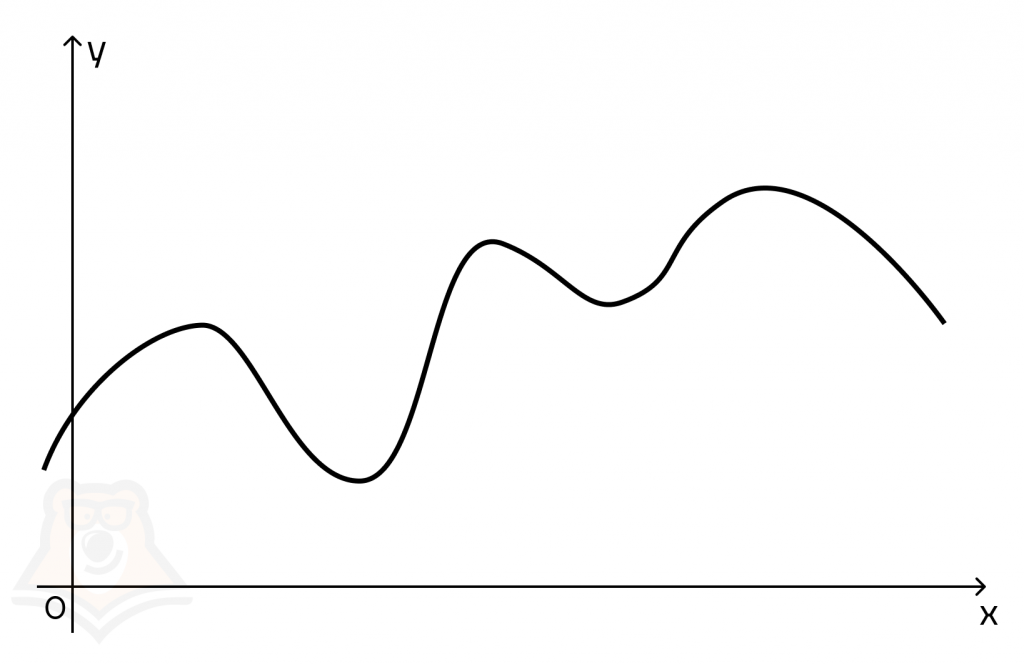
Функция будет на некоторых участках возрастать, а на некоторых убывать. Скорость ее изменения на разных участках будет разной.
Скорость изменения функции показывает, насколько сильно будет изменяться значение функции (то есть значение у) при небольшом изменении переменной функции (то есть значения х).
Отложим на нашем графике две точки: х и х1 и поднимем из них прямые, которые пересекут график в точках А и В. Тогда точка А будет иметь координаты (х;у), а точка В — (х1;у1).
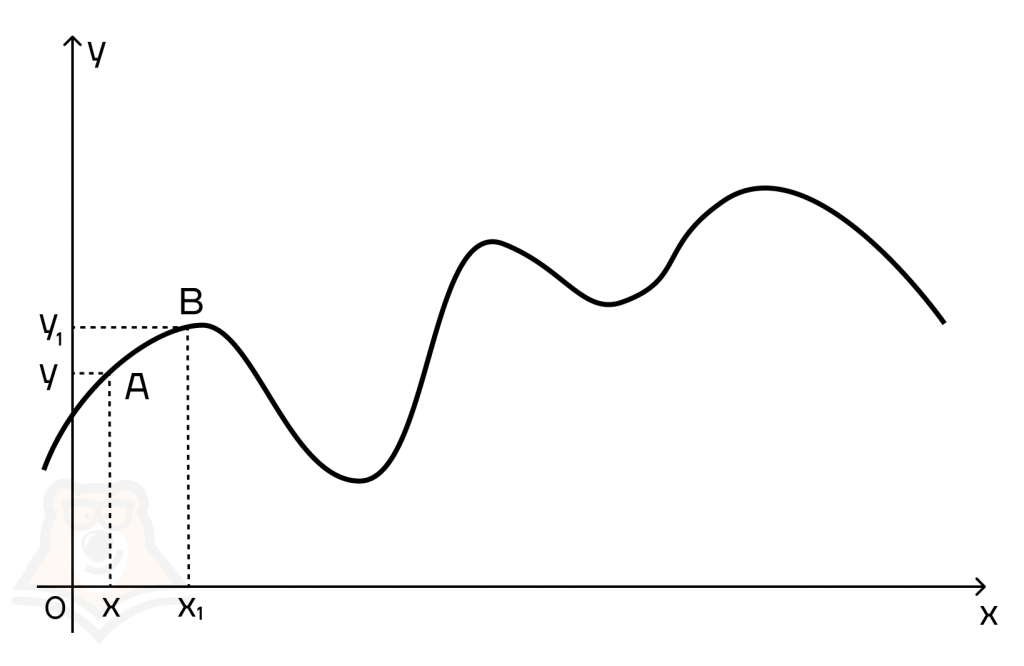
Представим, что наш вагончик проехал из точки А в точку В. Расстояние, которое он проехал по горизонтали, будет равно х1 — х, а поднялся он на высоту у1 — у. Для удобства дальнейших рассуждений примем эти расстояния за х и у.
Знак Δ “дельта” — означает изменение величины, то есть разность между тем, что было в точке А и стало в точке В.
Теперь мы можем ввести определение приращения.
Приращение функции — это разность между двумя значениями функции, то есть у.
Приращение аргумента — это разность между двумя значениями аргумента, то есть х.
Скорость изменения функции будет равна отношению приращения функции к приращению аргумента. При этом чем меньше будет приращение аргумента, тем точнее мы приблизимся к верному значению.
Отсюда мы получаем определение производной функции.
Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции.
Производную функции обозначают как f'(x).
(f'(x) = frac{Delta y}{Delta x}: при: Delta x rightarrow 0)
Если мы применим одинаковое приращение аргумента к разным участкам функции, то заметим, что приращение функции также будет разное. Где-то значение у изменится больше, где-то меньше. Именно так изменяется скорость функции на разных ее участках.
Нахождение производной называется дифференцированием.
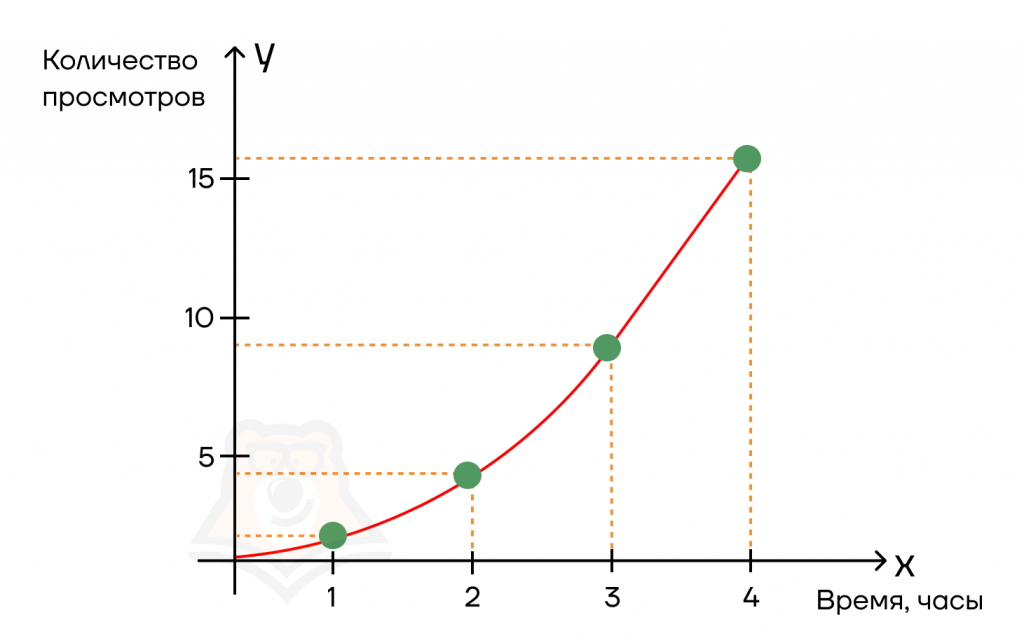
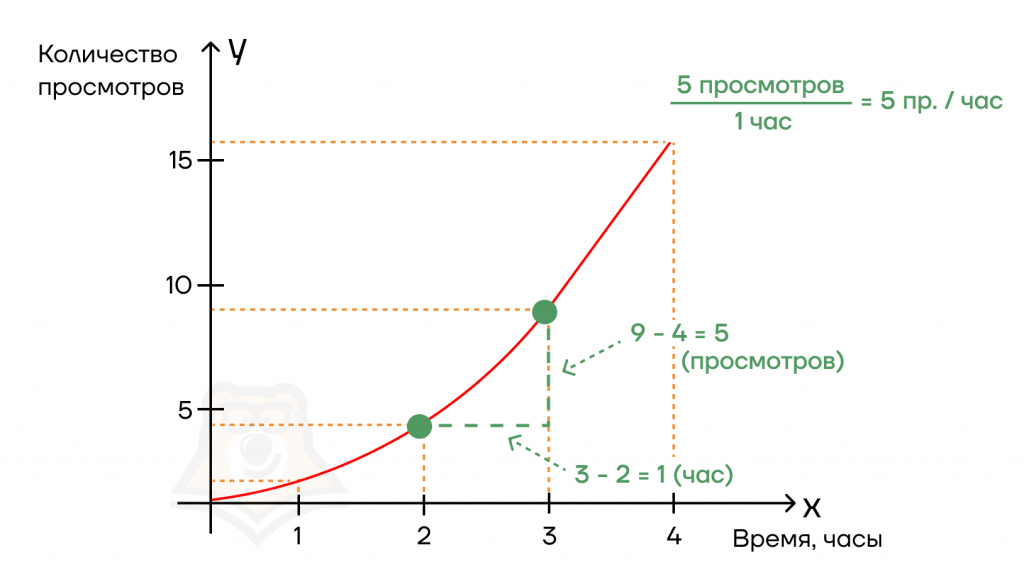
Допустим, мы выложили видео в соцсеть. Сначала было совсем невесело: за первый час всего один просмотр. За второй час ситуация сильно не изменилась — добавилось лишь 3 просмотра. Мы скинули ссылку на видео в чат друзей, и за третий час количество просмотров дошло до 9, а за четвертый час — до шестнадцати.
Возможно, ситуация не очень похожа на правду, и мы бы сразу попали в топ. Но пусть будет так для удобства цифр.
В результате мы имеем функцию, которая показывает, как количество просмотров менялось во времени.
Теперь зададимся вопросом: как быстро росла популярность у нашего ролика?
Чтобы это выяснить, мы возьмем две соседние точки на графике и посчитаем:
1) как изменилось количество просмотров между этими точкам (Δ количества просмотров);
2) как изменилось время между этими точками (Δ времени);
3) затем разделим Δ просмотров на Δ времени.
Получается, что “производительность” нашего видео была 5 просмотров в час.
Таким нехитрым образом, мы нашли производную от функции, показывающую рост популярности нашего ролика в сети за определенный промежуток времени:
(f'(x) = frac{Delta y}{Delta x} = frac{5}{1} = 5)(просмотров в час)
Геометрический смысл производной
Достроим прямоугольный треугольник АВС. Заметим, что отношение (frac{Delta x}{Delta y} = tg(BAC)), то есть равняется отношению противолежащего катета к прилежащему катету. Иначе это отношение можно записать как (tg(BAC) = frac{BC}{AC}).
Поскольку в этом примере мы взяли достаточно большое расстояние между значениями х, то АВ — секущая. Если мы будем сокращать расстояние между значениями аргумента, то две точки на графике будут ближе друг к другу, а секущая будет стремиться к касательной.

Следовательно, мы можем описать скорость изменения функции через тангенс угла наклона касательной, проведенной к графику функции в некоторой точке.
Из этих рассуждений мы можем вывести геометрический смысл производной:
Если провести касательную к функции в некоторой точке, то производная в этой точке будет равна тангенсу угла ее наклона.
Рассмотрим касательную отдельно. Это прямая, которая имеет уравнение y = kx+b, где к — коэффициент наклона.
Тогда мы получаем следующее уравнение:
f'(x) = k = tg(a)
Геометрический смысл производной — главный совместный номер. Производная равняется тангенсу угла наклона касательной, проведенной к функции в определенной точке.
Знак производной
Построим графики двух прямых с разным углом наклона. Пусть в первом случае k = 1, а во втором k = -1. Тогда получаем графики функций у = х и у = -х.
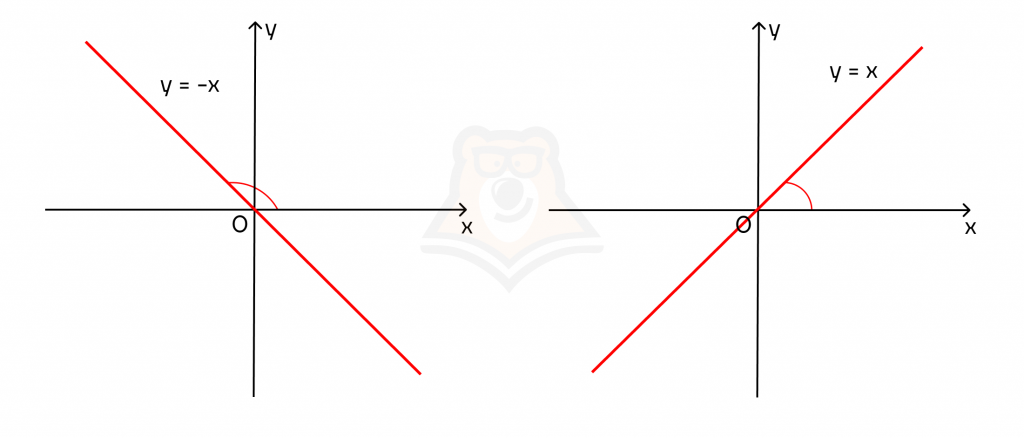
Заметим, что тангенс угла наклона имеет разные значения в этих случаях: tg(a) = -1 и tg(a) = 1.
Теперь достроим к касательным графики функций. В первом случае точка, к которой проведена касательная, будет лежать на участке функции, на котором она убывает. Во втором случае точка касания будет лежать на возрастающем участке функции.
Чтобы определить, убывает или возрастает функция, нужно посмотреть на ее наклон на участке.
Вспомним американские горки: пусть по функции будет слева направо ехать вагончик. В участках, где вагончик будет подниматься на гору, функция возрастает, а где вагончик съезжает с горки — функция убывает.
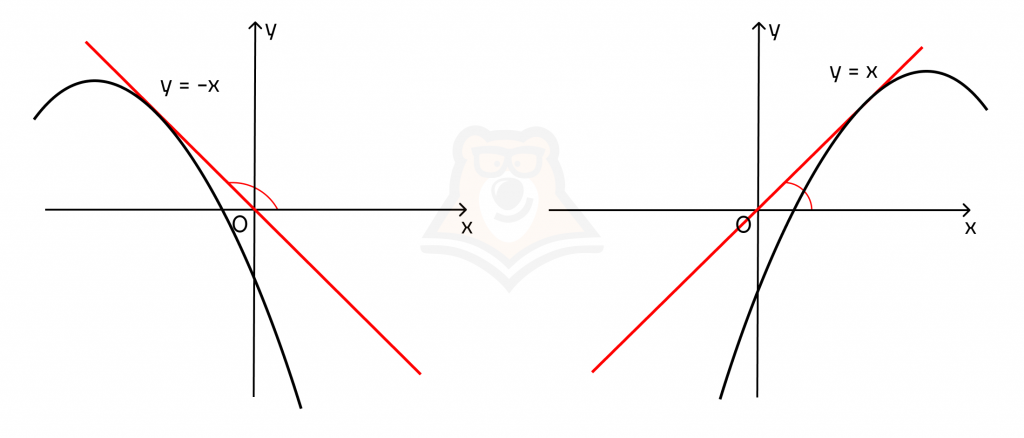
Из этих рассуждений мы можем вывести зависимость знака функции и знака производной.
1. Функция возрастает в точке тогда и только тогда, когда производная в данной точке положительна.
В этом случае касательная к функции также будет возрастать.
f'(x) = tg(a). Если tg(a) > 0, то и f'(x) > 0.
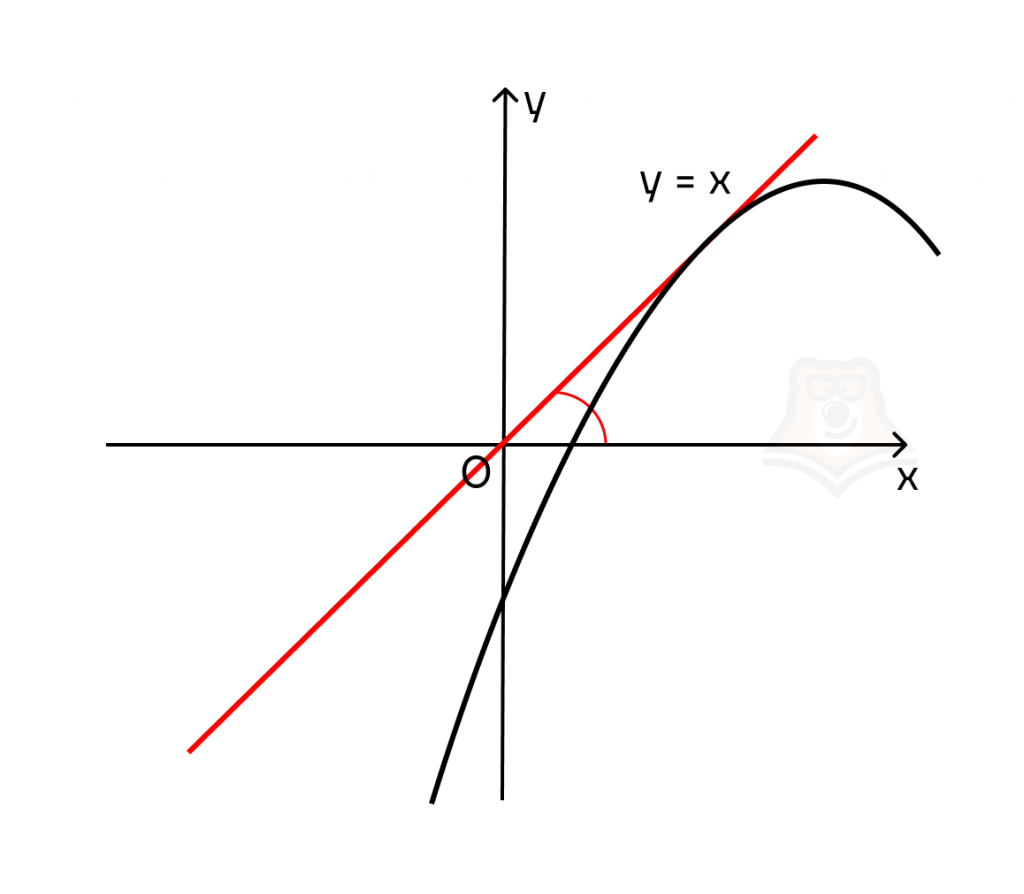
2. Функция убывает в точке тогда и только тогда, когда производная в данной точке отрицательна.
В этом случае касательная к функции будет убывать.
f'(x) = tg(a). Если tg(a) < 0, то и f'(x) < 0.

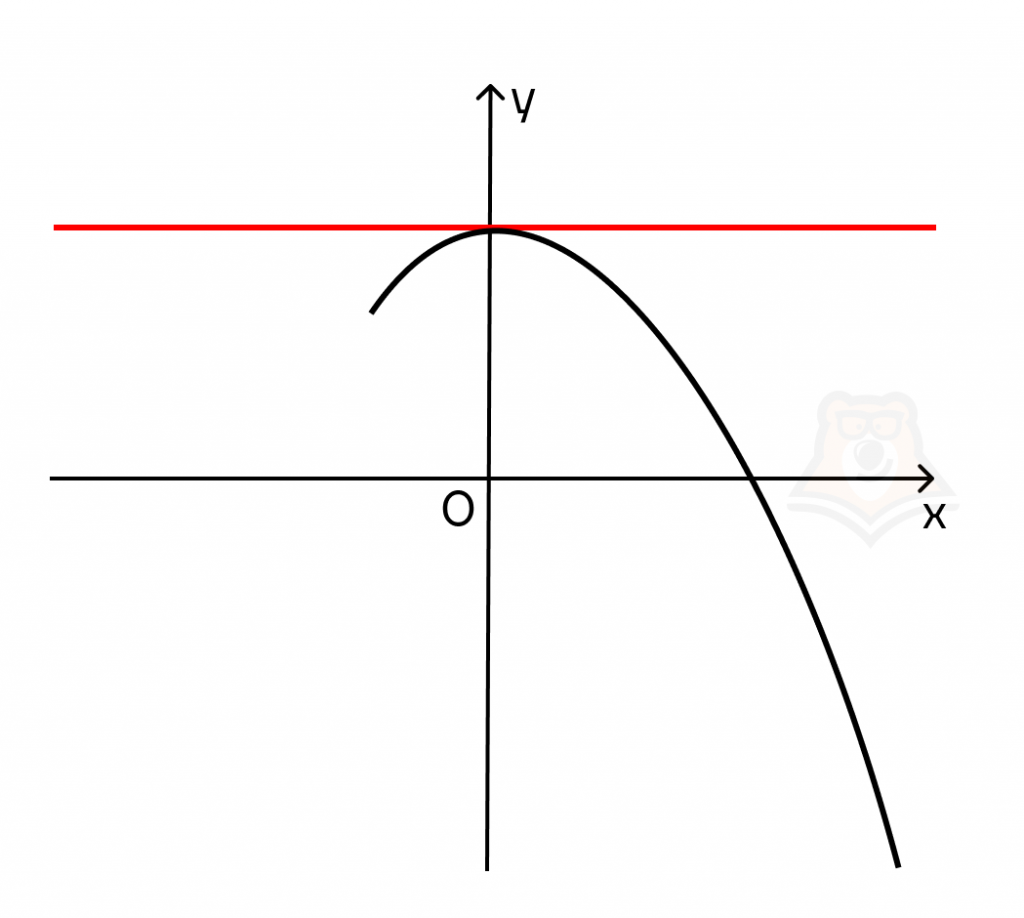
3. Если касательная к функции параллельна оси абсцисс, то производная в этой точке равна 0.
Поскольку прямая будет параллельна оси абсцисс, то у нее не будет угла наклона, а следовательно: k = tg(a) = 0 = f'(x).
Такие точки называются стационарными, это точки экстремума или седловые точки.
Подведем итог.
Знак производной определяется по изначальной функции:
- если функция возрастает, то производная положительна;
- если функция убывает, то производная отрицательна;
- в точках, где функция не возрастает и не убывает (стационарные точки), производная равна 0.
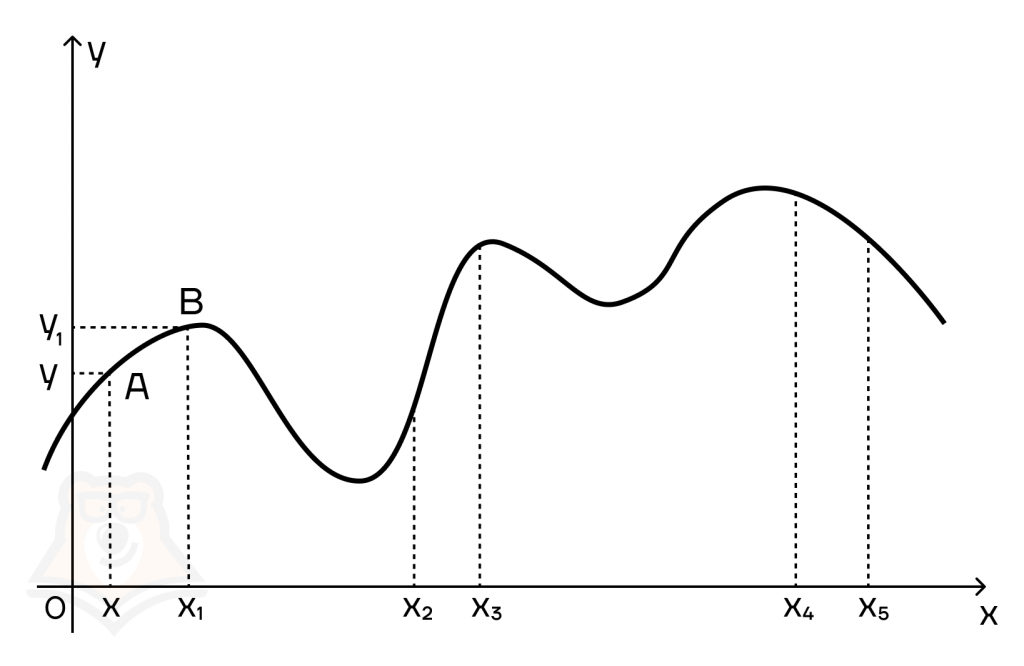
Точки экстремума
Как уже было сказано ранее, производная функции может равняться 0. Она принимает такое значение в точках экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.
Точки экстремума — точки, в которых достигается экстремум.
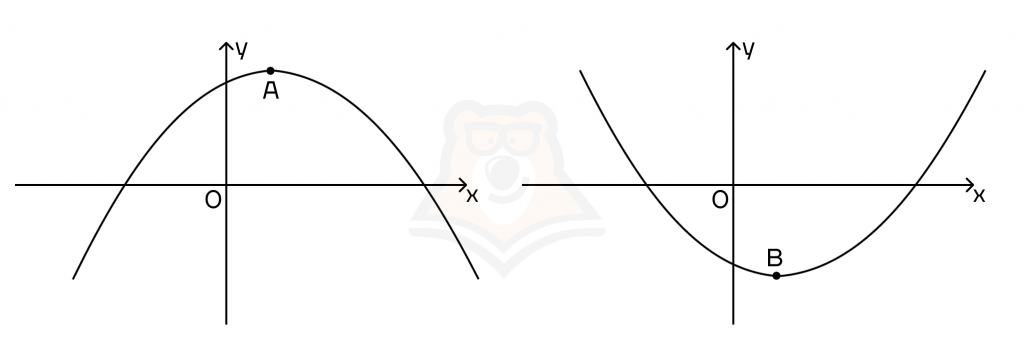
На рисунке видно, что точки А и В являются экстремумами. Например, до точки А функция будет возрастать, а после нее уже убывать, то есть наибольшее значение эта функция достигнет именно в точке экстремума.
Если вспомнить наш вагончик, то в точке А он достигнет наибольшую высоту над землей.
Во втором случае аналогичные рассуждения, но функция достигает уже наименьшее значение в точке В.
В теме производной есть такие термины, как “точка минимума” и “точка максимума”.
Точка минимума — это точка, в которой достигается минимальное значение функции.
В этой точке знак функции меняется с отрицательного на положительный (то есть сначала функция убывала, а потом начала возрастать). Это точка В.
Точка максимума — это точка, в которой достигается максимальное значение функции на отрезке.
В этой точке знак функции меняется с положительного на отрицательный (то есть сначала функция возрастала, а потом стала убывать). Это точка А.
Также с точками экстремума связаны наибольшее и наименьшее значение функции.
Важно!
Следует вспомнить, что когда мы говорим о значении функции, то имеем в виду значение ординаты, то есть у (или f(x)).
Наибольшее значение функции — точка на оси ординат, в которой достигается наибольшее значение функции на заданном отрезке.
Например, в точке А будет достигаться наибольшее значение функции.
Наименьшее значение функции — точка на оси ординат, в которой достигается наименьшее значение функции на заданном отрезке.
В точке В будет достигаться наименьшее значение функции.
Физический смысл производной
Предположим, что некоторая точка движется прямолинейно, и ее путь можно описать по закону х(t). То есть за определенное время t точка пройдет расстояние х.
А теперь вспомним формулу скорости: (v = frac{x}{t}).
Чтобы найти среднюю скорость на каком-то участке пути точки, нужно разделить весь путь на все время, или (v_{ср.} = frac{Delta x}{Delta t}). Таким образом, мы пришли к определению производной.
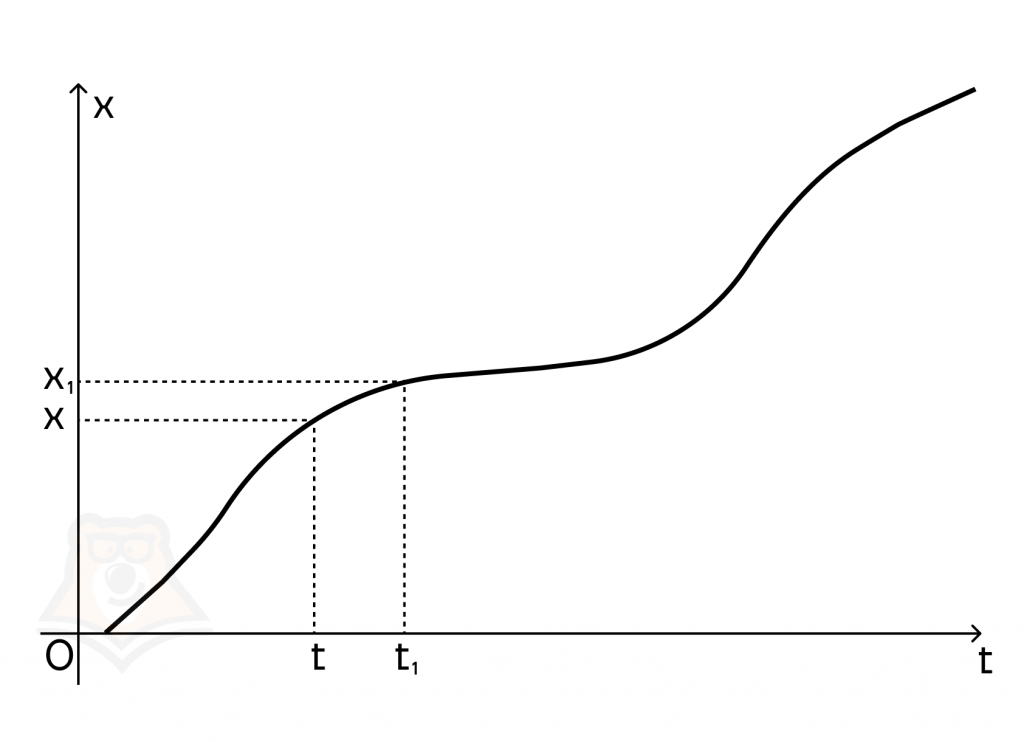
Физический (механический) смысл производной состоит в том, что производная от функции равняется скорости движения некоторого тела по траектории x(t) в момент времени t. x'(t) = v
Также вспомним, что скорость тела зависит от его ускорения. Тогда, применяя аналогичные рассуждения, получаем:
v'(t) = a
Производную можно брать несколько раз. Например, если мы дважды возьмем производную от x(t), то получим ускорение точки:
(x^{primeprime} (t) = v'(t) = a).
Как найти скорость и ускорение точки с помощью производной?
Для этого необходимо воспользоваться физическим смыслом производной: производная от функции равна скорости движения некоторого тела. Производная от скорости равна ускорению тела.
Фактчек
- Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции. Скорость изменения функции равняется отношению приращения функции к приращению аргумента. Нахождение производной называется дифференцированием.
- Если провести касательную к функции в некоторой функции, то производная в этой точке будет равна тангенсу угла ее наклона. Это геометрический смысл производной.
- Производная будет положительна на участках возрастания функции и отрицательна на участках убывания. В стационарных точках (точки экстремума и седловые точки) производная будет равна 0.
- Точка минимума — точка, в которой достигается минимальное значение на заданном отрезке, точка максимума — точка, в которой достигается максимальное значение.
- Физический (механический) смысл производной состоит в том, что производная от функции равняется скорости движения некоторого тела по траектории x(t) в момент времени t.
Термины
Абсцисса — координата определенной точки на оси Х.
Ордината — координата определенной точки на оси У.
Проверь себя
Задание 1.
Что такое приращение функции?
- Разность между значениями у;
- Разность между значениями х;
- Сумма значений у;
- Сумма значений х.
Задание 2.
Чему равна производная?
- Котангенсу угла наклона касательной;
- Тангенсу угла наклона касательной;
- Синусу угла наклона касательной;
- Косинусу угла наклона касательной.
Задание 3.
Как меняется знак производной в точке максимума?
- Знак производной не меняется;
- Производная всегда равна 0 и не имеет знака;
- Знак меняется с положительного на отрицательный;
- Знак меняется с отрицательного на положительный.
Задание 4.
В каком случае функция будет возрастать?
- Если производная положительна;
- Если производная отрицательна;
- Если производная равна 0;
- Ни один из вышеперечисленных случаев.
Задание 5.
Какая величина получится, если дважды взять производную у функции?
- Скорость;
- Ускорение;
- Путь;
- Время
Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 1
Возьмем любую функцию, например у = 2*х
И посмотрим как она изменится, например на отрезке от 2 до 3.
В точке х = 2 функция примет значение у = 4
В точке х = 3, у = 6.
То есть на этом отрезке функция изменилась на 2. Значит можно сказать, что скорость ее изменения на этом отрезке оказалась равной 2.
Теперь возьмем функцию у = 3*х
Легко увидеть, что она на этом же отрезке измениться на 3 (т. к. у (2) = 6, а у (3) = 9)
И обе эти функции на каждом единичном отрезке (от 2 до 3, или от 5 до 6, или от 99 до 100) всегда меняются на одну и ту же величину: у = 2*х всегда меняется на 2, а у = 3*х – на три. Поэтому скорости изменения этих функций постоянны.
Можно взять функцию посложней, например, у = х^2 (х в квадрате)
она в точке х = 2 равна 4, а в точке х = 3 равна 9. То есть на этом отрезке она увеличится на 5.
А на отрезке от 3 до 4 она измениться уже на 7 (16 – 9). То есть скорость изменения функции у = х^2 меняется, причем с ростом х она все время увеличивается.
Можно смотреть как меняется функция не только на единичом отрезке, но и на любом. Из физики помните, что такое скорость? Это пройденный путь деленный на время, так же и скорость изменения функции это ее изменение деленное на длину отрезка, на котором она менялась. Например, у = х^2. Если х меняется, например, от 1 до 5, то длина отрезка равна 4. а у = х^2 изменится на этом отрезке от 1 до 25, то есть на 24. Значит средняя скорость изменения функции на этом отрезке равна 24/4 = 6.
То есть чтобы найти среднюю скорость изменения нужно разделить изменение у на изменение х. Если изменение по оси х обозначить за t, то это можно записать (y(x + t) – y(x)) / t
Но обычно не очень интересно как функция меняется в среднем на большом отрезке, а наоборот, интересно как она меняется на каждом маленьком отрезке, в идеале в каждой точке. А чтобы узнать какая скорость изменения функции на маленьком отрезке, это значит сделать t как можно меньше, если мы устремим t к нулю, то узнаем скорость изменение функции в конкретной точке. Но (y(x+t) – y(x)) / t при t стремящемся к нулю, это как раз определение производной в точке х. Поэтому и говорят, что производная показывает скорость изменения функции (на самом деле Ньютон ее и придумал, чтобы уметь точно вычислять скорость изменения функции в точке) .
Например, в наших примерах производная функции у = 2*х в любой точке равна 2, вот мы и видели, что скорость изменения этой функции на любом отрезке была равна 2.
А производная у = х^2 равна 2*х. То есть производная и, соответственно, скорость изменения функции х в квадрате в каждой точке разная (в х = 1, производная равна 2, а в х = 100, производная равна 200), причем, чем больше х, тем быстрее скорость изменения.
План урока:
Предел функции на бесконечности
Предел функции в точке
Приращение аргумента и функции
Средняя скорость изменения функции
Мгновенная скорость и понятие производной
Предел функции на бесконечности
Рассмотрим довольно простую функцию
y = 1/x
Её график называется гиперболой и выглядит так:
Можно заметить, что при больших положительных значениях х график функции приближается к горизонтальной оси Ох, но не пересекает её. Действительно, если мы будем вычислять значение у при всё больших значениях х, то будем получать всё меньшие, но всё же положительные числа:
Получается, что при бесконечном росте аргумента х функция стремится к нулю. Можно ли эту особенность функции как-то записать, используя математические символы? Оказывается, можно, и выглядит это запись так:
которая означает, что х стремится к бесконечности. После символа lim записана сама функция 1/х. В целом вся запись читается так: «предел функции у = 1/х при х, стремящемся к бесконечности, равен нулю».
Вернемся к графику функции у = 1/х. Видно, что если мы будем брать всё меньшие отрицательные значения х, то функция также будет стремится к нулю. Действительно, попробуем подставлять в нее как можно меньшие значения аргумента:
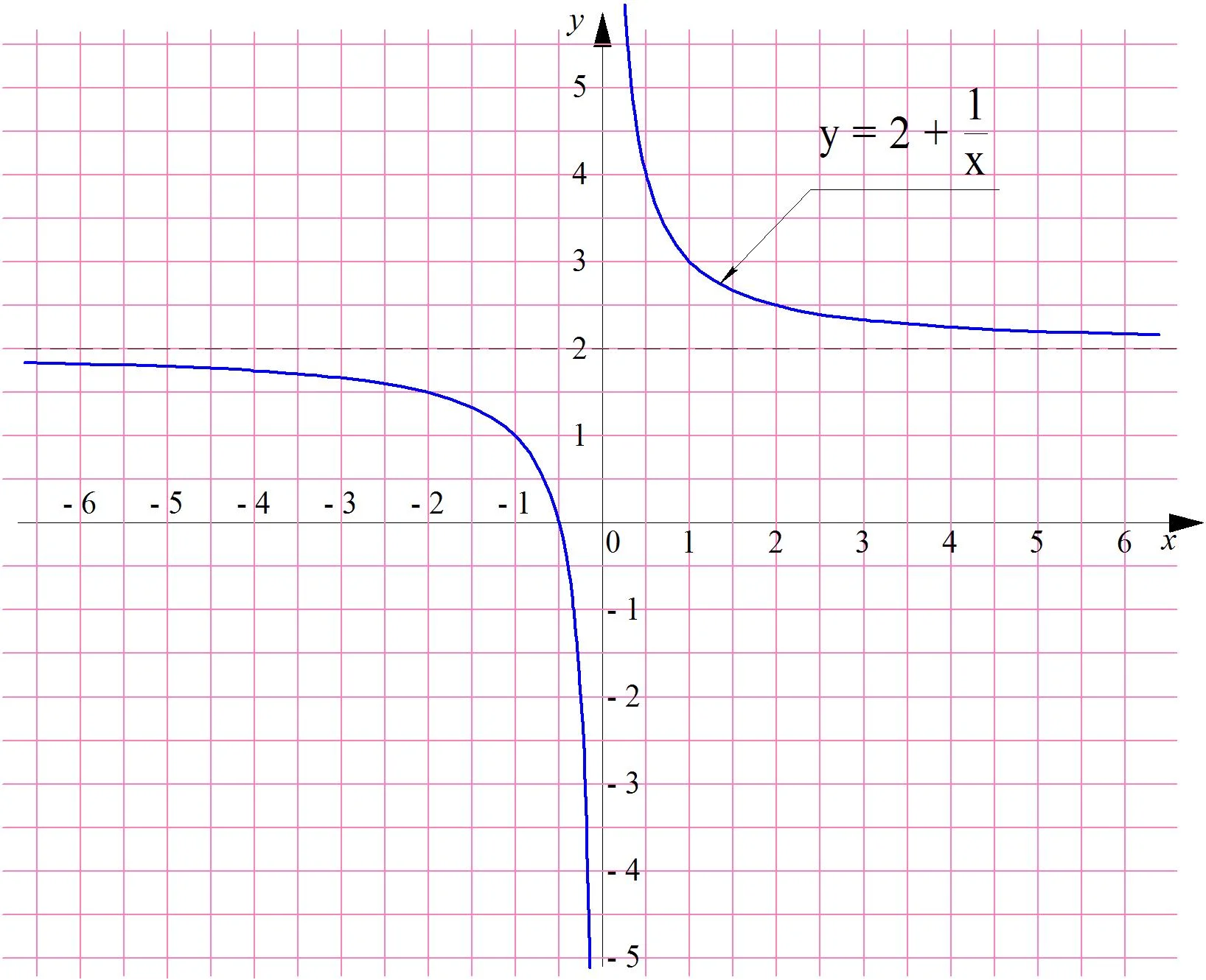
Чтобы записать эту особенность функции, используется следующая запись:
который может быть получен параллельным переносом графика у = 1/х на две единицы вверх:
Очевидно, что пределы этой функции при х → + ∞ и х → – ∞ равны 2:
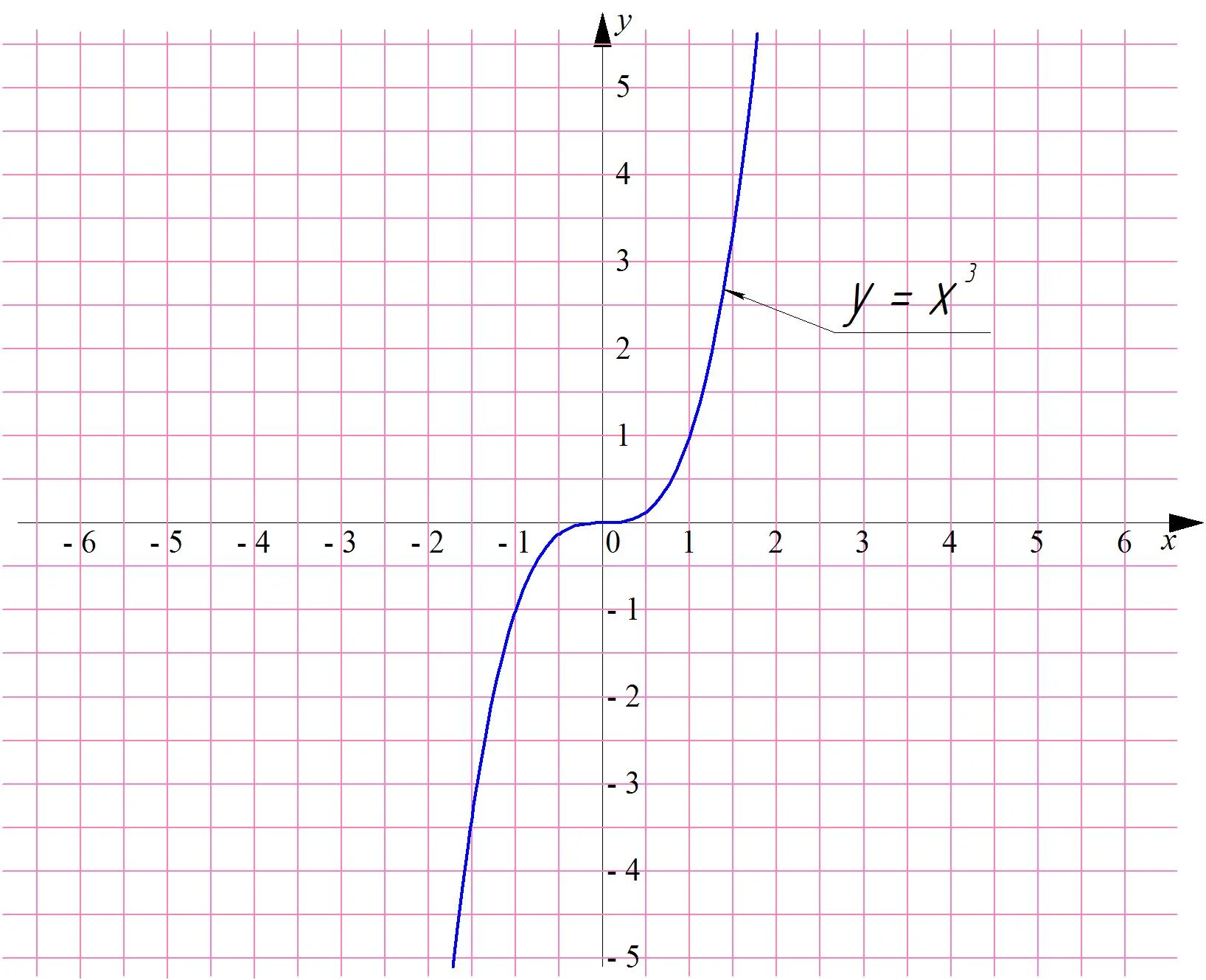
Возможны случаи, когда при бесконечном увеличении аргумента функции она не стремится к какому-то конкретному числу, а сама также неограниченно возрастает. Для примера посмотрим на график у = х3:
Видно, что при х → ∞ сама функция неограниченно растет, что можно показать расчетами:
Возникает вопрос – для всякой ли функции можно указать ее предел на бесконечности? Оказывается, что нет. Для примера рассмотрим тригонометрическую функцию у = sinx, графиком которой является синусоида:
С одной стороны, sinx явно не стремится к какому-то конкретному числу при увеличении х, он «колеблется» между числами 1 и (– 1). С другой стороны, нельзя и сказать, что он стремится к бесконечности. Получается, что у этой функции просто нет пределов на бесконечности.
Предел функции в точке
Порою нас интересует поведение функции не на бесконечности, а вблизи конкретной точки х0. Конечно, в большинстве случае можно просто вычислить функцию в этой точке, однако иногда это невозможно сделать. Для примера рассмотрим функцию
Очевидно, что точка х = 2 не входит в ее область определения, ведь при подстановке этого значения в функцию знаменатель дроби обратится в ноль. Однако в любой другой точке значение функции будет равняться единице:
График такой функции будет выглядеть как прямая у = 1, у которой есть одна «выколотая точка», соответствующая х = 2:
Итак, функция не определена в точке х = 2, однако можно вычислить предел функции в точке х = 2. Действительно, при любом, сколь угодно близком к 2 значении х функция будет равна единице:
Попробуем также приблизиться к точке 2 с другой стороны, подставляя в функцию числа, меньшие двух:
Снова всё время получается единица. Поэтому мы можем уверенно записать, что
Значительно чаще приходится иметь дело с пределами в точке, которые равны бесконечности. Снова посмотрим на график функции у = 1/х:
Видно, график не пересекает ось Оу, ведь число х = 0 не входит в область определения функции. Однако можно заметить, что при приближении х к нулю функция неограниченно возрастает:
Обратите внимание, что под пределом мы использовали запись «х → + 0», а не «х → 0». Почему? Дело в том, что если мы будем приближаться к нулю с «противоположной» стороны, подставляя в функцию не положительные, а отрицательные числа, то функция будет стремится к – ∞:
Получается, что предел функции в точке х = 0 зависит от того, с какой стороны мы приближаемся к этой точке, слева или справа. В связи с этим в математике существует понятие односторонних пределов. Для обозначения пределов, получаемых при приближении к нулю справа, то есть со стороны бОльших чисел, перед ним ставят знак плюс, а при указании предела слева, то есть со стороны мЕньших чисел – знак минус:
Предел и односторонние пределы – это два разных понятия. Считается, что функция имеет предел в точке только тогда, когда оба односторонних предела в этой точке совпадают.
В качестве ещё одного примера предела функции в точке можно привести зависимость у = tg х, график которой выглядит следующим образом:
В точке х = π/2 функция не определена. Однако видно, что при приближении к этой точке слева функция неограниченно возрастает, а при приближении справа – неограниченно убывает. Это записывается следующим образом:
До этого мы вычисляли пределы функций в точках, где сами функции не определены. Однако пределы можно вычислять и в тех точках, где функция определена. В большинстве случаев (но не всегда) они как раз равны значению функции в этой точке. Например, найдем предел
В точке х = 2 значение функции будет равно 4:
Будут ли односторонние пределы в этой точке также равняться 4? Сначала проверим предел справа
Действительно, получаем значения у, всё более близкие к 4. Аналогично можно убедиться, что и предел слева также равен 4:
Приведем несколько искусственный пример функции, у которой предел в точке не совпадает со значением функции в этой точке. Пусть функция задается с помощью такого графика
Он представляет собой параболу у = х2 с выколотой точкой (2; 4). При этом функция определена в точке х = 2, но имеет там значение, равное единице. Аналитически эту функцию можно описать так:
Понятно, что у(2) = 1, однако попытаемся приблизиться к точке х = 2 справа и слева и посмотрим, что получится:
Мы видим, что при х→2 функция и справа, и слева стремится к четверке, а не к единице. То есть получается, что предел функции в точке х = 2 не совпадает со значением функции этой функции в этой же точке. Такая ситуация произошла именно из-за того, что точка х = является выколотой.
Сразу заметим, что непосредственно в практических задачах пределы почти не используются. В связи с этим эта тема изучается в школьном курсе довольно поверхностно, не дается строгое определение предела функции (предполагается, что это понятие интуитивно понятно), а также не рассматриваются примеры на вычисление пределов функций. С другой стороны, на понятии предела построены почти все строгие рассуждения и доказательства в математическом анализе. В частности, определение понятие производной (которая имеет огромное практическое применение) дается именно с помощью предела. Поэтому полностью исключить пределы из школьного курса нельзя.
Приращение аргумента и функции
Часто нас интересует, как изменяется функция при изменении аргумента. Например, известно, что объем куба вычисляется по формуле
где а – ребро куба. Предположим, что мы провели измерения какого-то куба и выяснили, что длина его ребра равна 2 см. Тогда объем куба составит 23 = 8 см3. Но ведь любое измерение производится не с абсолютной точностью, а с некоторой погрешностью. Как оценить погрешность вычисления объема, если известна погрешность измерения его ребра?
Пусть с учетом погрешности линейки, составляющей 0,1 см, известно, что длина ребра находится в диапазоне от 2 до 2 + 0,1 = 2,1 см. Тогда максимально возможный объем куба составит 2,13 = 9,261 см3. Получается, что погрешность в измерении объема куба составляет 9,261 – 8 = 1,261 см3.
С точки зрения математического анализа мы в данном случае рассматривали поведение функции у = х3 в точке х = 2. Мы допустили некоторое изменение величины х, которое называют приращением аргумента и обозначают как ∆х. Далее мы высчитали, какое изменение величины у, или приращение функции, обозначаемое как ∆у, соответствует этому приращению аргумента. Выяснилось, что приращению ∆х = 0,1 соответствует приращение ∆у = 1,261.
В более общем случае произвольной функции у = f(x) можно дать некоторое приращение ∆х в некоторой точке х0. В результате этого изменится и само значение f(x), причем величину этого изменения обозначают как ∆у. Это можно проиллюстрировать графически:
Задание. Дана функция у = 3х2 + х + 4. Вычислите приращение функции в точке х0 = 5, если ∆х = 1.
Решение. Сначала вычислим новое значение аргумента функции, с учетом данного ему приращения:
Далее вычислим значения функции, соответствующие старому и новому аргументу:
Задание. Радиус круга, измеренный с погрешностью не более 0,5 см в меньшую сторону, равен 10 см. Оцените погрешность вычисления его площади.
Решение. Площадь круга рассчитывается по формуле:
Средняя скорость изменения функции
Часто в физике и других естественнонаучных дисциплинах одни величины характеризуют изменение других величин. Классический случай – это скорость, которая характеризует, насколько быстро изменилось положение тела (или материальной точки в пространстве). Рассмотрим пример. Пусть пешеход движется по прямой улице с постоянной скоростью 2 м/с. Попытаемся построить график, который иллюстрирует зависимость пройденного пешеходом пути и его скорости от времени. Известно, что при равномерном прямолинейном движении пройденный путь можно найти по формуле:
S = v*t
Где s – путь;
V – скорость;
t – время.
Так как скорость равна 2 м/с, то зависимость пути от времени будет выглядеть так:
s(t) = 2t
которая является прямой пропорциональностью. Поэтому ее график будет прямой линией:
Так как скорость во время всего движения остается равной 2 м/с, то зависимость скорости от времени будет иметь вид v = 2, а выглядеть она будет как горизонтальная линия:
В данном случае найти зависимости s(t) и v(t) было очень легко. Но теперь усложним задачу. Пусть зависимость s(t) задается не прямой линией, а некоторой кривой:
Можно ли теперь что-то сказать о скорости движения пешехода?
Ясно, что в различные моменты времени скорость пешехода различна. Но мы можем найти среднюю скорость пешехода в какой-то момент времени. Например, рассмотрим промежуток времени со 2-ой по 10-ую секунду.
Его протяженность, очевидно, равна 10 – 2 = 8 секундам. Если первый момент времени обозначить как t1, а второй как t2, то протяженность этого промежутка времени (∆t) можно вычислить по формуле
Судя по графику, к моменту времени t1 пешеход прошел только 1 метр, а на момент t2он преодолел уже 9,5 м. Сколько же метров он прошел за промежуток времени ∆t? Если первое расстояние обозначить как s1, а второе как s2, то пройденное расстояние (∆s) можно рассчитать так:
Тогда средняя скорость на рассматриваемом участке можно вычислить, поделив ∆s на ∆t
В данной ситуации мы рассматривали функцию, которая задает зависимость между перемещением пешехода и временем. Средняя скорость характеризует, как быстро двигается пешеход, то есть как быстро функция s(t) меняет своё значение. Очевидно, что в данном случае величина ∆t – это некоторое приращение аргумента функции s(t), в то время как ∆s– это приращение самой функции. Получается, что с помощью приращений можно вычислять среднюю скорость объектов.
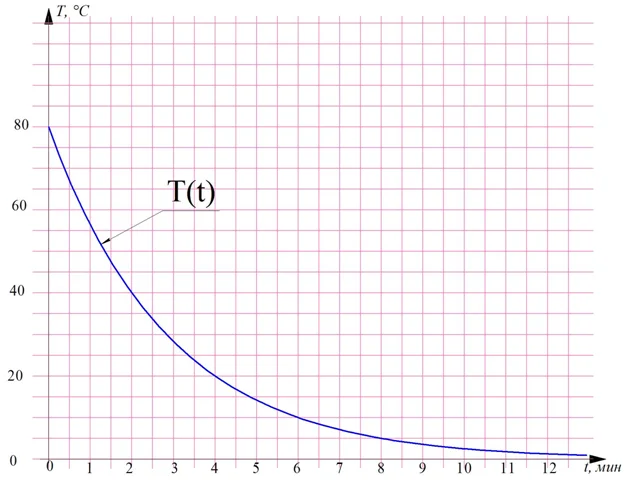
Однако в физике рассматривается не только скорость перемещения вточек пространстве. Например, можно говорить о скорости остывания горячего чайника. Пусть его температура меняется по закону, график которого представлен на рисунке:
Можно ли узнать, с какой средней скоростью остывал чайник на промежутках от 2-ой до 4-ой минуты? Да, для этого надо в точке t = 2 мин дать приращение аргумента ∆t = 2мин и посмотреть, какое приращение ∆T получит сама функция:
Пусть t1 = 2 мин, а t2 = 4 мин. Тогда
По графику видно, что в момент t1 температура чайника составляет Т1 = 40°С. Через две минуты она уже упала до отметки Т2 = 20°С. Получается, что за промежуток ∆t функция T(t) получила приращение
Обратите внимание, что приращение оказалось отрицательным. Дело в том, что температура чайника падала, то изменялась в меньшую сторону. Знак минус указывает именно на направление изменения функции. Если бы чайник нагревался, то приращение оказалось бы положительным.
Теперь мы можем вычислить среднюю скорость остывания чайника на промежутке между 2-ой и 4-ой минутой:
Знак минус указывает на то, что температура на этом промежутке времени уменьшается, а не возрастает.
В более общем случае, когда у нас есть произвольная функция у = f(x), с помощью приращений можно вычислить среднюю скорость её изменения на каком-нибудь промежутке. Пусть первая точка промежутка обозначается как х0, а его протяженность составляет ∆х. Тогда первой точке соответствует значение функции у(x0), а концу промежутка – значение у(x0 + ∆x):
Тогда средняя скорость изменения функции на промежутке [x0;x0 + ∆x] рассчитывается по формуле:
Мгновенная скорость и понятие производной
Итак, зная функцию, можно вычислить среднюю скорость ее изменения на любом промежутке. Но, когда автомобиль едет по шоссе, его спидометр показывает не среднее, а конкретное значение скорости в каждый момент времени. Другими словами, у автомобиля есть мгновенная скорость, и именно ее показывает спидометр. Как же узнать ее?
Пусть у нас есть функция s(t), определяющая пройденной машиной путь, и нам требуется найти мгновенную скорость в некоторый момент времени t1. Мы можем дать функции s(t) приращение ∆t, а потом найти и среднюю скорость на промежутке [t1; t1 + ∆t]. Естественно, она будет являться лишь некоторым приближением, с помощью которого мы оцениваем мгновенную скорость в момент t1. Однако далее мы можем уменьшить промежуток ∆t. Тогда у нас получится иное значение средней скорости, которое будет более близким к мгновенной скорости. Чем меньший промежуток ∆t мы возьмем, тем ближе к мгновенной скорости в точке t0 будет полученное нами значение средней скорости.
Например, пусть путь, пройденный машиной, задается функций s = t2. Нас интересует скорость автомобиля в момент t1 = 5 сек. Мы можем найти среднюю скорость на интервале от 5-ой до 6-ой секунды. Так, к пятой секунде машина успеет проехать 52 = 25 метров, а к шестой секунде она проедет 62 = 36 метров. Получится, что за промежуток ∆t, равный 6 – 5 = 1 секунде, машина проедет путь ∆s = 36 – 25 = 11 метров. Тогда средняя скорость на промежутке составит
Теперь возьмем более короткий промежуток ∆t, равный всего лишь 0,1 с. То есть мы рассмотрим период времени между моментом t1 = 5 cи t2 = 5,1 c. Снова-таки, к 5-ой секунде машина проедет 25 метров, а к моменту 5,1 сона пройдет 5,12 = 26,01 м. То есть за 0,1 с автомобиль преодолеет 26,01 – 25 – 1,01 м, а средняя скорость при этом составит
Ещё раз уменьшим промежуток ∆t. Пусть теперь он составляет всего 0,01с. Тогда средняя скорость будет определяться так:
Видно, что при уменьшении промежутка ∆t средняя скорость стремится к величине 10 м/с. Поэтому логично считать именно эту величину мгновенной скоростью машины в момент времени t = 5 c. Однако возникает вопрос – уверены ли мы, что мгновенная скорость стремится именно к 10 м/с, а не, скажем, к 10,001 м/с? Как точно определить это число? Здесь как раз помогают пределы. Можно записать, что мгновенная скорость – это предел отношения ∆s/∆t при ∆t, стремящемся к нулю. То есть
Получили, что мгновенная скорость в момент t1 = 5 действительно равна 10 м/с.
Задание. Вычислите мгновенную скорость разгоняющегося самолета через 10 секунд после начала разгона, если пройденное им расстояние задается законом s(t) = 5t2.
Решение. За 10 секунд самолет успеет преодолеть
Дадим функции s(t) приращение ∆t и обозначим как t1 момент времени, когда со старта прошло 10 секунд. Тогда к моменту t1 + ∆t самолет успеет пройти
Решая данную задачу, мы дали функции s(t) приращение ∆t и записали отношение ∆s/∆t. Далее мы устремили величину ∆t к нулю и посмотрели, к какому числу устремится отношение ∆s/∆t. Это число и оказалось мгновенной скоростью. В более общем случае произвольной функции у = f(x)в точке х0 можно дать приращение аргумента ∆х, которому будет соответствовать некоторое приращение функции ∆у. Далее можно вычислить предел отношения ∆у/∆х, который будет характеризовать, как быстро в точке х0 функция меняет свое значение. Этот предел называют производной функции в точке х0. Для обозначения производной над функцией ставят штрих.
В общем случае алгоритм вычисления производной в некоторой точке следующий:
1.Фиксируем точку х0, вычисляем для нее значение функции у(х). Это значение будет конкретным числом
- Даем функции приращение аргумента ∆х, переходим в новую точку х0 + ∆х, вычисляем в ней значение функции у(х0 + ∆х). Это значение будет не числом, а выражением, содержащим переменную ∆х.
- Находим приращение функции ∆у, используя формулу
Это приращение также должно содержать величину ∆х.
- Составляем соотношение ∆у/∆х.
- Находим предел этого отношения при ∆х→0. Этот предел и есть значение производной.
Задание. Найдите производную функции у = 4х2 + 7х в точке х0 = 2.
Решение. Сначала вычислим значение функции в точке х0:
Далее определяем величину у(х0 + ∆х) (это будет не конкретное число, а некоторое выражение, содержащее переменную ∆х):
Задание. Найдите производную функции у = 1/х в точке х0 = 5.
Решение. Высчитаем у(х0):
Пусть у функции есть приращение ∆х, тогда в точке х0 + ∆х ее значение составит:
В рассмотренных примерах для вычисления производной мы использовали ее определение. Однако на практике такой метод почти не используется. В будущем мы узнаем более эффективные способы для нахождения производной.
Мы уже убедились, что использование производной помогает находить мгновенную скорость тел. По этой причине понятие производной функции играет огромную роль в механике (разделе физике, изучающем движение). Однако этим ее практическое применение не ограничивается. По сути, она является основой для всей классической физики, и именно ее появление в XVII в. обеспечило выдающийся прогресс в науке вплоть до конца XIX в. При этом производная используется и в геометрии для анализа графиков функций. Более подробно ее применение будет также рассмотрено позже.
***************************************************************************
Материал подготовлен при поддержке SkillFactory. Скидка 45% по промокоду MATH-45 на все обучающие курсы по Data Science до 30.09! Записывайся!
***************************************************************************
“Современные проблемы требуют современных решений” – так гласит один из популярных мемов, давно гуляющих по просторам Интернета. Такой же подход принят и в Data Science – направлении науки об анализе данных: постоянно разрабатываются новые математические методы оптимизации, кластеризации и классификации, обучения нейросетей и многое другое.
Однако фундамент всего этого разнообразия остается незыблемым. Это всё те же “нелюбимые” логарифмы, синусы и косинусы, матрицы и тензоры, интегралы и производные.
Вот о последнем понятии мы и поговорим сегодня: начнем с определения и основных свойств, вспомнив прошлое, а затем узнаем как производная используется в задачах обучения нейронных сетей в настоящем. Поехали!
Что такое производная ?
Производная характеризует скорость изменения функции в данной точке. Помните самый простой пример из школьной физики: ускорение является первой производной от скорости (а еще второй производной по времени радиус-вектора). Так вот благодаря производной мы и можем утверждать в конкретный момент времени, ускоряется или замедляется объект.
Классическое определение производной в школьной математике дается через предел:
На этом графике показана функция f(x) произвольного вида. Δx – приращение аргумента функции. Предел отношения изменения функции при стремлении приращения аргумента Δx к нулю и называется производной функции в точке (в данном случае в x ₀ ).
Чтобы наглядно понять, как это происходит посмотрите на рисунок: при стягивании отрезка приращения аргумента (красная линия) уменьшается и размах изменения функции (зеленая линия). В какой то момент это отношение становится равным определенному числу, имеющему очень важный геометрический смысл:
Значение производной в точке x ₀ равняется тангенсу угла наклона касательной к графику функции в этой точке. Это свойство ОЧЕНЬ сильно понадобится нам в дальнейшем.
Не буду дублировать здесь значения табличных производных и правила для сложных функций: их и так легко найти в сети. Приведу лишь самый простой и конкретный пример, который вычислю по определению:
Что еще дает производная ?
Самое важное практическое значение производной в том, что с её помощью удается исследовать функции на экстремумы : минимумы и максимумы. Дело в том, что, если производная больше или равна нулю на интервале (a,b), то функция f строго возрастает на этом интервале, а если наоборот – то строго убывает.
Необходимым условием существования экстремума у функции на некотором интервале в точке x ₀ является либо равенство нулю, либо отсутствие производной.
Достаточным условием является смена знака производной при переходе через x ₀ : если знак меняется с плюса на минус, то функция имеет максимум, если наоборот – то минимум.
Вывод: производную в школе изучают, в основном, для умения исследовать функции на экстремумы. А что дальше?
Частные производные и градиент функции
До этого мы рассматривали лишь функции от одной переменной. Что же будет, если их две, три или больше. В таком случае вычисляются частные производные:
Градиент – это вектор, показывающий направление наибольшего возрастания функции. Вычисляется он, как Вы уже догадались, через частные производные (если аргументов у функции больше двух, конечно же). Вычислим градиент:
Что делать с полученными значениями? А вот что: берем точку, например А = (1,1,3) и вычисляем координаты градиента и его длину. В итоге мы получаем направление и скорость изменения функции в данной точке!
На свойстве градиента показывать “направление” и “скорость движения” основан такой метод нахождения локальных экстремумов функции, как градиентный спуск. Суть метода заключается в движении в направлении экстремума с шагом (шагами) определенной длины.
В Data Science, где повсеместно применяются искусственные нейронные сети, метод используется для нахождения минимума функции ошибок – квадрата разности расстояний от выходных сигналов персептрона до их требуемых значений.
В реальных примерах обучения нейронных сетей, где количество выходов может исчисляться десятками и сотнями, естественно никакой речи о визуализации и быть не может: всё происходит в n-мерном пространстве, что, однако, не отменяет свойств градиента по поиску экстремума.
Итак, после прочтения статьи у Вас есть базовые понятия о производной и градиенте функции.
*****************************************************************************
Хотите знать больше и применять математику на практике, при этом неплохо зарабатывая? В этом случае хочу порекомендовать Вам курсы Data Science от онлайн-школы SkillFactory.
Полный курс состоит из шести огромных модулей, призванных развить все возможные компетенции, необходимые для Data Scientist’a.
Учебная программа в SkillFactory построена таким образом, что обучиться этой современной, востребованной и ОЧЕНЬ высокооплачиваемой профессии можно с нуля, имея только школьное образование! На всех этапах обучения студентов поддерживают наставники курса, а выпускникам помогают с трудоустройством.
Посмотреть учебную программу и цены на курсы
До 30.09 действует скидка 45 % по промокоду math-45!