Как найти скорость изменения ускорения - Сайт, где вы сможете решить свои вопросы

Скорость, ускорение и время являются основными величинами для вывода уравнения движения. В общем, производная скорости по времени дает ускорение.

В кинематике скорость можно найти, используя ускорение и время. С скорость и ускорение связаны с величиной и направлением, для определения скорости мы используем как алгебраический метод, так и интегральное исчисление. В этом посте обсуждается, как найти скорость с учетом ускорения и времени, используя оба метода.

Представим, что тело движется с ускорением «а», преодолевая определенное расстояние в момент «t».

Алгебраическим методом:

Из кинематического определения ускорение – скорость изменения скорости движущегося тела.

а=в/т

Здесь мы считаем; первоначально тело обладает минимальной скоростью; следовательно, начальная скорость можно считать примерно равной нулю.

Переставляя члены, мы получаем скорость тела как;

v = а * т

Методом интегрального исчисления:

Производная по времени от скорость дает ускорение тела. Это определяется следующим уравнением.

d/dt[v(t)]= а(t)

Преобразуя приведенное выше уравнение

dv (t) = a (t) dt

Интегрируя приведенное выше уравнение по времени t

∫d/dt[v(t)]=∫a(t) dt+C

Где; C – интегральная постоянная.

Следовательно; v = при + C

Вышеприведенное уравнение дает скорость; таким образом, умножение ускорения на время дает скорость.

Кредиты изображения: Изображение предоставлено Долоресбарриослуа от Pixabay

Как найти скорость по графику ускорения и времени?

Построен график ускорения в зависимости от времени, что позволяет определить различные физические величины, такие как рывки и удары. скорость. Область, покрытая графиком «ускорение – время», показывает скорость.

Например, машина движется с начальной скоростью 16 м / с. Как со временем, машина начинает разгоняться. В ускорение автомобиля постоянна во времени. Через некоторое время машина внезапно останавливается, что показано на приведенном ниже графике.

График, чтобы показать, как найти скорость с ускорением и графиком времени

Пунктирная линия используется как контрольная линия, когда тело останавливается.

Площадь, занимаемая в график ускорение – время представляет собой прямоугольник. Площадь прямоугольника определяется как

А = l × b

Из приведенного выше графика длина прямоугольника – это ускорение, а ширина – время; следовательно, уравнение

А = а * т

Но площадь графика at – это скорость, тогда

v = а * т

v = 7 × 8

v = 56 м / с.

Следовательно, по определению На графике времени разгона площадь – это не что иное, как скорость.

Как найти начальную скорость с ускорением и временем?

Когда тело начинает двигаться из одной точки в другую, вначале оно обладает некоторой скоростью. Тело не нуждается постоянная скорость пока не достигнет конечного пункта назначения. Скорость тела изменяется со временем по мере его прохождения, и, следовательно, тело приобретает ускорение.

Из приведенного выше объяснения ясно, что движущееся тело может иметь разные скорости. Тела скорость на начальном этапе может отличаться от финального. Давайте обсудим нахождение скорости с ускорением и временем в начальной точке.

Рассмотрим сначала автомобиль, движущийся со скоростью v_i, а его скорость изменится через некоторое время t. Теперь тело ускоряется с ускорением «а», и, наконец, когда оно достигает конечной точки, оно имеет скорость v_f.

Начальную скорость можно рассчитать тремя способами.

Используя алгебраический метод:

Ускорение из-за изменения скорости определяется выражением

а = (v_f-v_i)/т

а * т = v_f – v_i

О перестановке

v_i = V_f – в

Вышеприведенное уравнение дает начальную скорость движущегося тела.

По расчетам:

Исходя из определения ускорения, уравнение имеет вид

а=дв/дт

Изменение условий;

адт = дв

Интегрируя приведенное выше уравнение, выбирая пределы в качестве начальной скорости vi в момент времени t = 0 и конечной скорости v_f в момент t.

а (t – 0) = (v_f – v_i)

при = v_f – v_i

Преобразуя приведенное выше уравнение, мы получаем начальную скорость.

v_i = V_f – в

Графическим методом:

Построен график зависимости скорости от времени, наклон которого дает ускорение – затем, найдя наклон, можно вычислить начальную скорость.

vt график показать, как найти скорость с ускорением и время

Исходя из приведенного выше графика, мы можем сказать это.

В единый интервал времени скорость тела изменяется.
OD – время, затрачиваемое телом на путешествие, а BD – конечная скорость тела.
Перпендикулярные линии от BD к A проводятся параллельно OD. Таким же образом проводится линия BE параллельно OD.

На приведенном выше графике показано, что

Начальная скорость тела v_i = ОА

Конечная скорость тела v_f = БД

На графике BD = BC + DC

Следовательно, v_f = ВС + ПОС

Но DC = OA = v_i

v_f = до нашей эры + ви

На графике наклон = ускорение a

а=ВС/АС

Но AC = t (из графика)

а=БК/т

при = BC

Подставляя значение BC

v_f = при + v_i

v_i = V_f – в

Как найти изменение скорости в зависимости от ускорения и времени

В общем, изменение скорости со временем дает ускорение.

Пусть тело движется с ускорением ‘a’ со временем ‘t’, изначально скорость объекта равна v_i, а в конечной точке имеет скорость v_f. Тогда изменение скорости определяется по уравнению:

∆a=(Δv/Δt)

Где ∆v – изменение скорости, а ∆t – изменение во времени.

∆v = ∆a∆t

Но изменение скорости определяется разница между начальной и конечной скоростью. Это дается уравнением ниже.

∆v = v_f -v_i

Изменение в скорость можно рассчитать с помощью графика “ускорение – время”. Площадь под графиком at показывает изменение скорости.

Давайте ясно поймем это, рассмотрев пример, представленный графиком, приведенным ниже.

Площадь на графике времени ускорения представляет собой треугольник. Следовательно, вычисляя изменение скорости дается путем вычисления площади треугольника. Формула для определения площади треугольника:

А=(1/2)чб

Здесь h – высота треугольника, ускорение считается высотой, а b – основание треугольника, которое определяется осью времени. Таким образом, изменение скорости равно

∆v=(1/2)*6*9

∆v = 29 м / с.

По изменению скорости мы можем узнать начальную и конечную скорость тела.

Решены задачи о том, как найти скорость с ускорением и временем.

Задача 1) Лодка движется с начальной скоростью 11 м / с. Лодка развивает ускорение 3 м / с.² каждые 10 секунд. Затем рассчитайте изменение скорости и конечную скорость лодки.

Решение:

Данные приведены для расчета:

Начальная скорость лодки v_i = 11 м / с.

Изменение ускорения, достигаемого лодкой a = 3 м / с².

Изменение по времени t = 10 сек.

∆v = ∆a∆t

∆v = 3 × 10

∆v = 30 м / с

Чтобы найти окончательную скорость, уравнение

∆v = v_f -v_i

v_f = ∆v + v_i

v_f = 30 + 11

v_f = 41 м / с.

Задача 2) График ускорение – время приведен ниже. Найдите изменение скорости и вычислите начальную скорость, если конечная скорость равна 54 м / с.

График ускорения-времени

Решение:

Приведенные данные:

Конечная скорость v_f = 54 м / с. На графике ускорение-время покрытая область представляет собой трапецию. Таким образом, площадь трапеции определяется выражением

А=[(а+б)/2)]*ч

Где a и b – прилегающее основание трапеции, h – высота. Из графика; a = 9 единиц, b = 5 единиц, h = 4 единицы.

А=[(9+5)/2]*4

А = 28 шт.

Изменение скорости равно площади трапеции.

∆v = 28 м / с.

Чтобы найти начальную скорость

∆v = v_f -v_i

v_i = V_f – ∆v

v_i= 54 – 28

v_i = 26 м / с.

Задача 3) дается график ускорение – время для определения изменения скорости.

Решение:

Приведенный выше график можно разделить на три части, представленные пунктирной линией, как показано на рисунке ниже.

На приведенном выше графике можно понять следующие термины.

OAD и BCE – треугольник; площадь треугольника задается формулой

а=(1/2)чб

ABCD – прямоугольник; площадь прямоугольника определяется выражением

А = l × b

Чтобы найти изменение скорости, необходимо вычислить сумму площадей всех геометрических структур.

∆v = A=(1/2)hb+lb+(1/2)hb

Изменение скорости ∆v = 180 м / с.

Задача 4) Найдите начальную скорость мяча, который ускоряется со скоростью 6 м / с.² со временем 8 сек. Конечная скорость мяча составляет 100 м / с.

Решение:

Приведены данные: ускорение мяча a = 6 м / с2.

Время t = 8 сек.

Конечная скорость v_f = 100 м / с.

Для нахождения начальной скорости тела задается уравнение

v_i = V_f – в

v_i = 100 – (6 × 8)

v_i = 100 – 48

v_i = 52 м / с.

Задача 5) Рассчитайте изменение скорости движущегося объекта, имеющего начальную скорость 34 м / с. Ускорение объекта 12 м / с.², а изменение по времени – 7 сек.

Решение:

Данный:

Начальная скорость объекта v_i = 34 м / с.

Ускорение объекта a = 12 м / с².

Изменение по времени t = 7 сек.

Конечная скорость объекта определяется выражением;

v_f = V_i + в

v_f = 34 + (12 * 7)

v_f = 34 + 84

v_f = 118 м / с.

Изменение скорости определяется выражением;

∆v = v_f – v_i

∆v = 118 – 34

∆v = 84 м / с.

Задача 6) Диск движется с начальной скоростью 25 м / с. Диск меняет свою скорость каждые 10 секунд. Изменение ускорения 5 м / с.². Рассчитайте конечную скорость диска.

Решение:

Приведенные данные:

Начальная скорость диска v_i = 25 м / с.

Изменение ускорения ∆a = 5 м / с².

Изменение времени ∆t = 10 сек.

Изменение скорости равно

∆v = ∆a∆t

∆v = 5 × 10

∆v = 50 м / с.

Конечная скорость диска может быть рассчитана по формуле, приведенной ниже.

∆v = v_f – v_i

50 = в_f -25

v_f = 50 + 25

v_f = 75 м / с.

Источник

Равноускоренное движение в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного падения

Равноуско́ренное движе́ние — движение тела, при котором его ускорение постоянно по модулю и направлению^[1].

Скорость при этом определяется формулой

${displaystyle {vec {v}}(t)={vec {v}}_{0}+{vec {a}}t}$

где ${displaystyle {vec {v}}_{0}}$ — начальная скорость тела, — время. Траектория имеет вид участка параболы или прямой.

Примером такого движения является полёт камня, брошенного под углом alpha к горизонту в однородном поле силы тяжести: камень летит с постоянным ускорением , направленным вертикально вниз.

Частным случаем равноускоренного движения является равнозамедленное, когда векторы vec{v} и противонаправлены, а модуль скорости равномерно уменьшается со временем (в примере с камнем реализуется для ${displaystyle alpha =90^{0}}$ при подъёме).

Характер равноускоренного движения[править | править код]

Равноускоренное движение происходит в плоскости, содержащей векторы ускорения и начальной скорости ${displaystyle {vec {v}}_{0}}$ . С учётом того, что (здесь — радиус-вектор), траектория описывается выражением

${displaystyle {vec {r}}(t)={vec {r}}_{0}+{vec {v}}_{0}t+{frac {{vec {a}}t^{2}}{2}}}$

На заданном интервале времени она представляет собой участок параболы, который при параллельности (то есть со или противо- направленности) векторов и ${displaystyle {vec {v}}_{0}}$ превращается в отрезок прямой.

Для каждой из координат, скажем , могут быть записаны аналогичные по структуре выражения:

${displaystyle y(t)=y_{0}+v_{0y}t+{frac {a_{y}t^{2}}{2}}}$

где ${displaystyle a_{y}}$ — составляющая ускорения вдоль оси , а ${displaystyle {vec {r}}_{0}=x_{0}{vec {i}}+y_{0}{vec {j}}+z_{0}{vec {k}}}$ — радиус-вектор материальной точки в момент ( vec{i} , vec{j} , vec{k} — орты).

В примере с камнем ${displaystyle x_{0}=y_{0}=z_{0}=0}$ , компоненты ускорения ${displaystyle a_{x}=a_{z}=0}$ , ${displaystyle a_{y}=-g}$ , начальной скорости ${displaystyle v_{x0}=v_{0}cos alpha }$ , ${displaystyle v_{y0}=v_{0}sin alpha }$ , ${displaystyle v_{z0}=0}$ , при этом ${displaystyle x(t)=v_{0x}t}$ , а значит, ${displaystyle y=operatorname {tg} alpha cdot x-g/2v_{0}^{2}cos ^{2}alpha cdot x^{2}}$ .

Перемещение и скорость[править | править код]

В случае равноускоренного движения любая из компонент скорости, например ${displaystyle v_{x}}$ , зависит от времени линейно:

${displaystyle v_{x}=v_{0x}+a_{x}t}$

При этом имеет место следующая связь между перемещением ( ${displaystyle Delta x=x-x_{0}}$ ) вдоль координаты и скоростью вдоль той же координаты:

$Delta x={frac {v_{x}^{2}-v_{{0x}}^{2}}{2a_{x}}}$

Отсюда можно получить выражение для -составляющей конечной скорости тела при известных -составляющих начальной скорости и ускорения:

$v_{x}=pm {sqrt {v_{{0x}}^{2}+2a_{x}Delta x}}$

Если ${displaystyle a_{x}=0}$ , то ${displaystyle v_{x}=v_{ox}}$ , а ${displaystyle Delta x=v_{0x}t}$ .

Выражения для смещений Delta y , Delta z и компонент скорости вдоль координат и принимают точно такой же вид, как для Delta x и $v_{x}$ , но символ всюду заменяется на или .

Суммарно, по теореме Пифагора, перемещение составит

${displaystyle |Delta {vec {r}}|={sqrt {(Delta x)^{2}+(Delta y)^{2}+(Delta z)^{2}}}}$

а модуль конечной скорости находится как

$|{vec v}|={sqrt {v_{{x}}^{2}+v_{{y}}^{2}+v_{{z}}^{2}}}$

Равноускоренное движение не может происходить неограниченно долго: это означало бы, что, начиная с какого-то момента времени , модуль скорости тела превысит величину скорости света в вакууме , что исключается теорией относительности.

Условие осуществления[править | править код]

Равноускоренное движение реализуется при действии на тело (материальную точку) постоянной силы vec{F} , обычно в однородном гравитационном или электростатическом поле, если величина скорости тела значительно меньше, чем скорость света . Тогда, по второму закону Ньютона, ускорение составит

${vec {a}}={frac {{vec {F}}}{m}},$

где через обозначена масса тела. В примере с камнем роль vec{F} играет сила тяжести.

Если же скорость тела сопоставима со скоростью света, то закон Ньютона в выписанном виде неприменим. При этом, в случае действия постоянной силы, происходит так называемое релятивистски равноускоренное движение, при котором постоянно только собственное ускорение, а ускорение в фиксированной ИСО приближается к нулю со временем по мере приближения величины скорости к её пределу .

Теорема о кинетической энергии точки[править | править код]

Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:

$ma_{x}Delta x={frac {mv_{x}^{2}}{2}}-{frac {mv_{{0x}}^{2}}{2}}$

Записав аналогичные соотношения для координат и и просуммировав все три равенства, получим соотношение:

${displaystyle {vec {F}}cdot Delta {vec {r}}={frac {mv^{2}}{2}}-{frac {mv_{0}^{2}}{2}}}$

Слева стоит работа постоянной равнодействующей силы vec F , а справа — разность кинетических энергий в конечный и начальный моменты движения. Полученная формула представляет собой математическое выражение теоремы о кинетической энергии точки для случая равноускоренного движения^[2].

Равнопеременное движение[править | править код]

Равнопеременным называется движение, при котором тангенциальная (параллельная скорости) составляющая ускорения постоянна^[3]. Такое движение не является равноускоренным, кроме ситуации, когда оно происходит по прямой, но в математическом плане может быть рассмотрено аналогично.

В этом случае вводится обобщённая координата , часто называемая путём, соответствущая длине пройденной траектории (длине дуги кривой). Таким образом, формула приобретает вид:

$Delta S={frac {v^{2}-v_{{0}}^{2}}{2a_{tau }}}$

где $a_{tau }$ — тангенциальное ускорение, «отвечающее» за изменение модуля скорости тела. Для скорости получаем:

$v=pm {sqrt {v_{{0}}^{2}+2a_{tau }Delta S}}$

При ${displaystyle a_{tau }=0}$ имеем движение с постоянной по модулю скоростью.

Иногда прилагательное равнопеременное заменяют на криволинейное равноускоренное, что вносит путаницу, так как, скажем, равноускоренное движение камня по кривой (параболе) в поле тяжести не равнопеременное.

См. также[править | править код]

Релятивистски равноускоренное движение

Примечания[править | править код]

↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 37. — 560 с. — ISBN 5-9221-0225-7.
↑ Тарг С. М. Краткий курс теоретической механики. — 11-е изд. — М.: «Высшая школа», 1995. — С. 214. — 416 с. — ISBN 5-06-003117-9.
↑ См. Физический энциклопедический словарь — М.: Советская энциклопедия, под. ред. А. М. Прохорова (1983), статья «Равнопеременное движение», стр. 602.

Источник

В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь – x нулевое- начальная координата. v нулевое – начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.

Примеры равноускоренного движения:

разгон самолета перед взлетом;
падающая с крыши сосулька;
торможение лыжника на горном склоне;
разгоняющийся на склоне сноубордист;
свободное падение в результате прыжка с парашютом;
камень брошенный под углом к горизонту;

Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

V_к=V_н+at

где: V_к — конечная скорость тела,
V_н — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.

Формула для ускорения при равноускоренном движении:

a=(V_к-V_н)/t

Во время движения тела ускорение остается постоянным.

Задача 1

Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.

Формула расстояния при равноускоренном движении

Если известны время, скорость начальная и скорость конечная

S = t*(V_н+ V_к)/2

Если известны время, скорость начальная и ускорение

S = V_нt + at²/2 **= t*(V_н + at/2)**

где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

2аS = V_к²−V_н²

где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.

Задача 2

Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.

Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.

Равноускоренное движение: графически

График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.

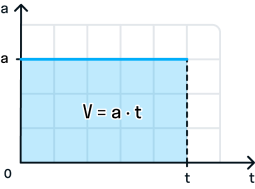
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.

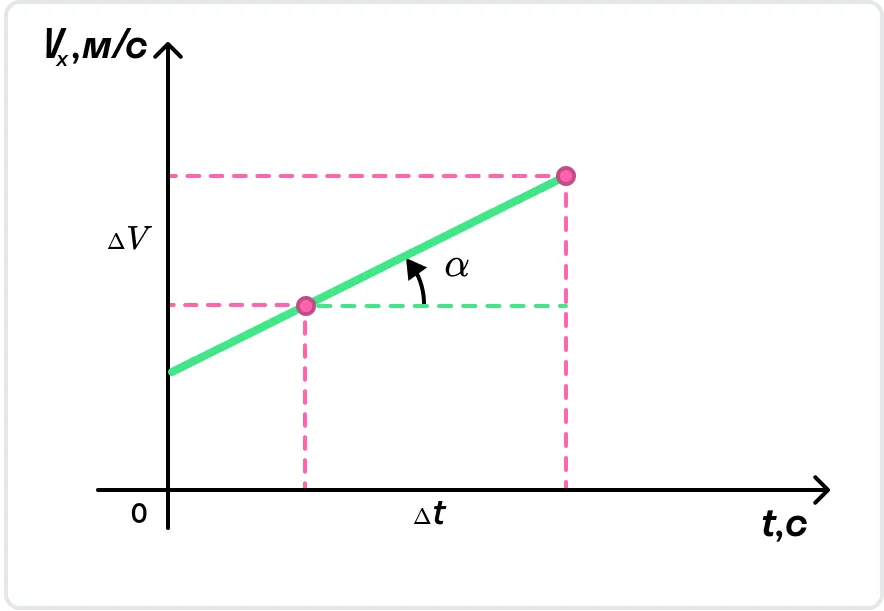
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V_нt и треугольника at²/2. Получим: S = V_нt + at²/2.

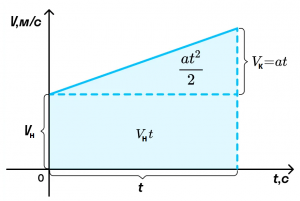
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.

Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = V_к²−V_н²
Получим: а = (V_к²−V_н² )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = V_нt + at²/2.
Получаем: x(t) = 3t + 1,5t²
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*2² =6+6=12 м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.

Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:

Конвертер единиц измерения расстояния (длины)
Конвертер единиц измерения скорости
Конвертер единиц измерения времени

Источник

Ускорение

4.3

Средняя оценка: 4.3

Всего получено оценок: 311.

Обновлено 6 Августа, 2021

4.3

Средняя оценка: 4.3

Всего получено оценок: 311.

Обновлено 6 Августа, 2021

Из курса физики 9 класса известно, что движение бывает равномерным и неравномерным. При неравномерном движении за равные промежутки времени материальная точка проходит разные расстояния, мгновенная скорость её движения также изменяется. Мера быстроты изменения скорости называется ускорением. Поговорим на эту тему, дадим определение ускорения, приведём его формулу.

Ускорение движения

Большинство движений в природе неравномерны. Если рассмотреть такое движение, то расстояния, проходимые за одинаковые промежутки времени будут разными. Следовательно, и скорость (она равна отношению пройденного расстояния ко времени прохождения) тоже будет разной.

Рис. 1. Пример неравномерного движения.

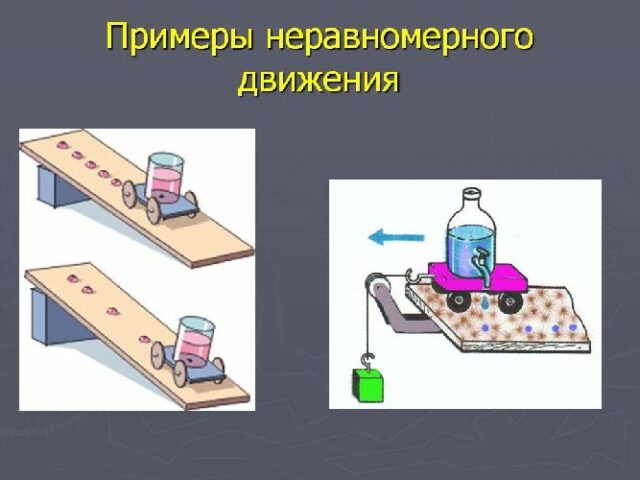
Более того, для разных движений изменение скорости за одинаковые промежутки времени также будет неодинаково. К примеру, рассмотрим разгон мяча и автомобиля. К концу разгона и тот и другой могут достичь мгновенной скорости 50 метров в секунду. Однако автомобиль достигает такой скорости за десять секунд, а мяч — в сто раз быстрее, за одну десятую секунды. Как охарактеризовать такое различие?

Физическая величина, характеризующая быстроту изменения скорости, называется ускорением.

Формулу ускорения легко получить, если учесть, что скорость — это быстрота изменения координаты, а ускорение — это быстрота изменения скорости:

$$overrightarrow a={overrightarrow v – overrightarrow {v_0} over t}$$

где:

$overrightarrow a$ — вектор ускорения;
$overrightarrow {v_0}$ — вектор начальной скорости;
$overrightarrow v$ — вектор скорости в момент времени $t$;
$t$ — время изменения скорости от $overrightarrow {v_0}$ до $overrightarrow v$.

Фактически ускорение — это «скорость изменения скорости». Поэтому формула ускорения аналогична формуле скорости, только в числителе вместо координаты стоит скорость.

Из приведённой формулы можно получить единицу измерения ускорения. Поскольку скорость в системе СИ измеряется в метрах в секунду, а время — в секундах, то ускорение получается в метрах в секунду в квадрате (иногда говорят метр в секунду за секунду).

Рис. 2. Ускорение в физике.

Равноускоренное движение

По аналогии со скоростью ускорение может быть средним и мгновенным. Мгновенное ускорение — это ускорение, для которого промежуток времени измерения стремится к нулю:

$$overrightarrow a_{мгн}={overrightarrow v – overrightarrow {v_0} over t},trightarrow 0$$

В противном случае ускорение получается средним за время $t$.

Движение, при котором мгновенное ускорение в любой момент времени остаётся постоянным и равным среднему ускорению за любой промежуток времени, называется равноускоренным. При равноускоренном движении скорость изменяется по линейному закону.

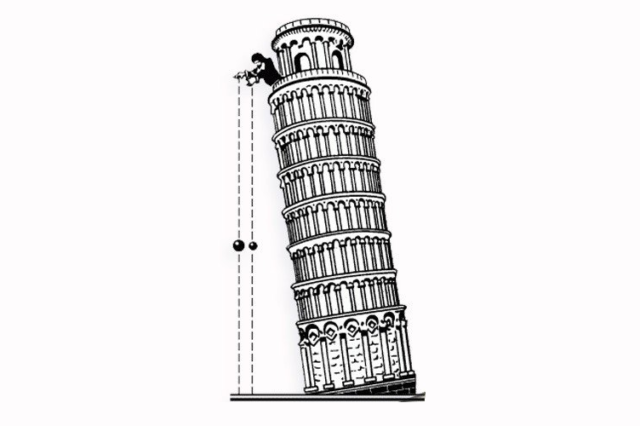
Примером равноускоренного движения является свободное падение тела в первые секунды, когда сопротивление воздуха ещё пренебрежительно мало.

Рис. 3. Свободное падение тела.

Что мы узнали?

Быстроту изменения скорости характеризует такая физическая величина, как ускорение. Единица измерения ускорения — метр в секунду за секунду. Движение, при котором мгновенное ускорение постоянно в любой момент времени, называется равноускоренным.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Лиза Глазунова

5/5

Оценка доклада

4.3

Средняя оценка: 4.3

Всего получено оценок: 311.

А какая ваша оценка?

Источник

Как найти скорость по графику ускорения и времени?

Как найти начальную скорость с ускорением и временем?

Как найти изменение скорости в зависимости от ускорения и времени

Решены задачи о том, как найти скорость с ускорением и временем.

Задача 2) График ускорение – время приведен ниже. Найдите изменение скорости и вычислите начальную скорость, если конечная скорость равна 54 м / с.

Задача 3) дается график ускорение – время для определения изменения скорости.

Задача 4) Найдите начальную скорость мяча, который ускоряется со скоростью 6 м / с.2 со временем 8 сек. Конечная скорость мяча составляет 100 м / с.

Задача 5) Рассчитайте изменение скорости движущегося объекта, имеющего начальную скорость 34 м / с. Ускорение объекта 12 м / с.2, а изменение по времени – 7 сек.

Задача 6) Диск движется с начальной скоростью 25 м / с. Диск меняет свою скорость каждые 10 секунд. Изменение ускорения 5 м / с.2. Рассчитайте конечную скорость диска.

Характер равноускоренного движения[править | править код]

Перемещение и скорость[править | править код]

Условие осуществления[править | править код]

Теорема о кинетической энергии точки[править | править код]

Равнопеременное движение[править | править код]

См. также[править | править код]

Примечания[править | править код]

Траектория, радиус-вектор, закон движения тела

Перемещение и путь

Скорость и ускорение

Закон равноускоренного движения

Пример решения задачи

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

Vк=Vн+at

Формула для ускорения при равноускоренном движении:

a=(Vк-Vн)/t

Задача 1

Формула расстояния при равноускоренном движении

S = t*(Vн+ Vк)/2

S = Vнt + at2/2 = t*(Vн + at/2)

2аS = Vк2−Vн2

Задача 2

Перемещение при равноускоренном движении

Равноускоренное движение: графически

Задача 3

Ускорение

Ускорение движения

Равноускоренное движение

Что мы узнали?

Тест по теме

Оценка доклада

Вам также может понравиться

Как найти письмо от гибдд

Как составить список имущества для банкротства

Формула как найти процент снижения

Добавить комментарий Отменить ответ

Задача 4) Найдите начальную скорость мяча, который ускоряется со скоростью 6 м / с.² со временем 8 сек. Конечная скорость мяча составляет 100 м / с.

Задача 5) Рассчитайте изменение скорости движущегося объекта, имеющего начальную скорость 34 м / с. Ускорение объекта 12 м / с.², а изменение по времени – 7 сек.

Задача 6) Диск движется с начальной скоростью 25 м / с. Диск меняет свою скорость каждые 10 секунд. Изменение ускорения 5 м / с.². Рассчитайте конечную скорость диска.

V_к=V_н+at

a=(V_к-V_н)/t

S = t*(V_н+ V_к)/2

S = V_нt + at²/2 **= t*(V_н + at/2)**

2аS = V_к²−V_н²