Как найти скорость качели

Дано:

m = 40 кг

Р = 800 Н

L = 2,5 м

g = 10 м/с²

υ – ?

Решение:

Распишу подробно.

Рассмотрим качель с ребёнком в нижней точке траектории качели. Ребёнок действует на качель весом Р. Сама качель по Третьему закону Ньютона действуют на ребёнка с такой же по модулю силой, что и он – на неё. Силой реакции опоры N:

N = P

Если теперь рассмотреть все силы, которые действуют на ребёнка в нижней точке, то получим силу тяжести mg и силу реакции опоры N. Кроме того, ребёнок движется криволинейно (траектория качели не прямая). Значит, какая-то сила заставляет его двигаться так. И этой силой является равнодействующая силы тяжести mg и силы реакции опоры N.

Силу, действующую на тело, которое движется с ускорением (а криволинейное движение – это всегда движение с ускорением), находят по Второму закону Ньютона:

F = ma, где а = υ²/R => F = mυ²/R

Длина подвеса качели – это и есть радиус кривизны движения качели (а значит и рассматриваемого тела – ребёнка), следовательно, конечный вид формулы будет следующим:

F = mυ²/L

Остаётся только представить равнодействующую F.

Сила тяжести mg – это сила, с которой Земля притягивает ребёнка, значит она направлена вниз, к земной поверхности. Сила реакции опоры N сопротивляется весу ребёнка P, который направлен туда же, куда и сила тяжести mg. Значит N будет направлена вверх, в противоположную сторону. Равнодействующая F удерживает ребёнка так, что он не падает вниз. Значит, F направлена туда же, куда и N.

Обеспечим все силы, которые направлены в одну и ту же сторону, знаком “+”. Все силы, которые направлены в противоположную сторону – знаком “-“. Например, силу тяжести mg запишем со знаком “-“. Тогда уравнение равнодействующей будет таким:

F = N + (-mg) = N – mg

Т.к. F = mυ²/L, то:

N – mg = mυ²/L – выражаем скорость:

(N – mg)*L = mυ²

(N – mg)*L/m = υ²

υ² = NL/m – mgL/m

υ² = NL/m – gL

υ² = L*(N/m – g)

υ = √(L*(N/m – g)) = √(2,5*(800/40 – 10)) = √(2,5*(20 – 10)) = √(2,5*10) = √25 = 5 м/с

Ответ: 5 м/с .

Рассмотрим в качестве модели качелей маятник переменной длины. Когда качающийся приседает, его центр тяжести опускается, и длина маятника увеличивается. Когда качающийся распрямляет ноги, центр тяжести поднимается, и длина маятника уменьшается.

Пусть наш маятник уже качается с небольшой амплитудой. Мгновенно уменьшим длину маятника в момент прохождения им нижней точки. Из закона сохранения момента импульса следует, что при этом произведение скорости маятника на его длину не изменится. Таким образом, скорость маятника — и, соответственно, энергия — возрастет. Обладая большей энергией, маятник отклонится на больший угол. В момент наибольшего отклонения длину маятника можно вернуть к исходной величине. Повторяя процесс периодически, можно раскачивать маятник всё сильнее.

Можно привести и математический расчет. Пусть в нижней точке длина маятника изменяется от величины L₁ к величине L₂ < L₁. Тогда скорость маятника возрастает: v₂ = v₁·L₁/L₂. Применяя закон сохранения энергии и считая углы малыми, можно найти величины отклонений φ₁ и φ₂: φ_i = v_i/(gL_i)^1/2, где i = 1, 2. Отсюда φ₂/φ₁ = (L₁/L₂)^3/2. То есть, например, если изменять длину маятника на 10%, увеличение амплитуды составит около 15% за один проход, или около 30% за период.

Вернемся теперь от модели к исходной задаче. Становится ясно, что качели будут раскачиваться, если приседать в моменты максимального отклонения, а распрямлять ноги в момент прохода нижней точки. Для оценки рассмотрим ситуацию, когда расстояние от оси качелей до центра тяжести системы «качающийся + качели» составляет 2 метра, а приседает он так, что центр масс опускается на 20 см. Тогда, по формуле из предыдущего параграфа, раскачка происходит со скоростью около 30% за период, то есть довольно быстро.

Подумайте также над следующими вопросами. Во-первых, за счет чего происходит увеличение энергии качелей? Во-вторых, разобравшись с качанием стоя, попробуйте описать механизм качания сидя, когда качающийся сидит на качелях и периодически сгибает-разгибает ноги и перемещает туловище. Ответы можно писать в комментариях к задаче.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Содержание книги

Предыдующая страница

§17. Механические колебания

17.8 Параметрические колебания. Качели.

С детства все хорошо знакома и многими любима такая старинная забава как качели. Тренировкам на этом снаряде придает большое значение даже летчики и космонавты. Когда малыша, сидящего на качелях, раскачивает кто-то из старших, стоящий рядом, то такой механизм разгона и поддержания колебаний нами подробно изучен – это вынужденные колебания под действием внешней периодической силы. Но на качелях можно раскачиваться самостоятельно, сидя или стоя на них. Процедура раскачивания в этом случае заключается, в том, что человек, стоящий на качелях, периодически, в нужные моменты приседает и встает. При этом периодически изменяются параметры самой колебательной системы (момент инерции, расстояние от точки подвеса до центра масс), поэтому такие незатухающие колебания называются параметрическими. Простейшим уравнением, описывающим такие эти колебания, может быть знакомое нам уравнение гармонических колебаний, в котором параметр ω² является периодической функцией времени

(~a = -omega^2(t) x) . (1)

Зависимость параметра от времени может быть, например, представлена в виде

(~omega^2(t) = omega^2_0 (1 + varepsilon cos omega t)) . (2)

где постоянная ω²₀ – собственная частота колебаний при неизменных средних значениях параметров системы (например, частота свободных колебаний качелей при неподвижно стоящем на них человеке), а второе слагаемое описывает периодическое изменение параметров системы.

Не смотря на внешнюю простоту этого уравнения, его анализ и решение очень сложны^[1], поэтому мы рассмотрим параметрические колебания качелей с энергетической точки зрения.

Когда человек приседает и встает он совершает работу, поэтому в принципе, может увеличивать амплитуду колебаний и компенсировать неизбежные потери механической энергии на трение и сопротивление воздуха. Подчеркнем, что в рассматриваемом случае источник энергии находится «внутри» самой колебательной энергии, причем этот источник должен расходовать энергию «сознательно», включаясь и выключаясь в нужные моменты времени. Обратим также внимание, на то обстоятельство, что рассматриваемая система не является замкнутой – раскачиваться на незакрепленных качелях, по меньшей мере, затруднительно. Наконец, движение человека относительно качелей должно быть периодическим, то есть время от времени, он должен возвращаться в исходное положение (сколько раз присел, столько раз встал).

Используем эти общие соображения для описания раскачивания качелей. Предельно упростим ситуацию – будем считать человека материальной точкой, расстояние от которой до оси вращения может изменяться в некоторых небольших пределах «сознательно», то есть в нужные моменты времени. Для того, чтобы максимально увеличить механическую энергию колебаний, человек должен вставать, когда для этого требуется приложить максимальное усилие, так как при этом будет совершена максимальная работа. Очевидно, что это условие достигается, когда качели проходят нижнюю точку. Если человек будет приседать в другом месте, то потери механической энергии при этом будут меньше, чем работа, совершенная при вставании в нижней точке. Таким образом, имеется возможность поддерживать незатухающие колебания.

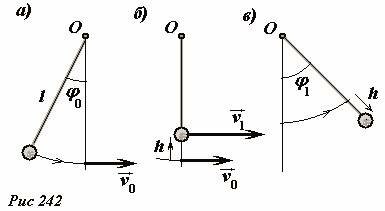
Итак, пусть начальный угол отклонения качелей равен φ₀ и при этом максимальном отклонении центр масс находится на максимальном удалении l от точки подвеса O (Рис. 242а). Когда качели опустятся под действием силы тяжести в нижнее положение, рассматриваемая материальная точка приобретет скорость υ₀, которую можно найти на основании закона сохранения энергии

(~frac{m upsilon^2_0}{2} = mgl (1 – cos varphi_0)) , (3)

из которого следует

(~upsilon^2_0 = sqrt{2 gl (1 – cos varphi_0)}) . (4)

Далее пусть в момент прохождения нижней точки центр масс очень быстро поднимается на малую высоту h (Рис. 242б), при этом его скорость возрастет до некоторой величины υ₁. Проще всего найти эту скорость на основании закона сохранения момента импульса

(~m upsilon_0 l = m upsilon_1 (l – h)) , (5)

из этого уравнения находим

(~upsilon_1 = upsilon_0 frac{l}{l – h} approx upsilon_0 left( 1 + frac{h}{l} right)) . (6)

на последнем шаге мы использовали приближенную формулу, считая, что высота подъема h значительно меньше длины качелей l.

Этот же результат можно получить и на основании рассмотрения энергетического баланса. Так в нижней точке сила давления человека на качели равна (эта формула непосредственно следует из уравнения второго закона Ньютона)

(~F = frac{m upsilon^2_0}{l} + mg) . (7)

Чтобы приподнять тело, к нему следует приложить такую же по модулю силу, направленную вверх. Следовательно, при этом необходимо совершить работу (delta A approx Fh) (это выражение является приближенным, так как, строго говоря, эта силы незначительно должна изменять в при вставании). Эта работа идет на увеличение кинетической и потенциальной энергии тела

(~Fh approx left( frac{m upsilon^2_2}{2} – frac{m upsilon^2_0}{2} right)+ mgh) . (8)

Это уравнение позволяет найти выражение для скорости

(~upsilon_1 = upsilon_0 sqrt{1 + 2 frac{h}{l}} approx upsilon_0 left( 1 + frac{h}{l} right)) , (9)

которое совпадает с выражением (6), полученным на основании закона сохранения импульса. Отличия в малых величинах порядка (~left( 1 + frac{h}{l} right)^2) обусловлены приближенным выражением для совершенной работы. Можете быть уверены, что при точном расчете работы (с учетом изменения силы при изменении расстояния до точки подвеса) эти два подхода дают полностью совпадающие результаты, совпадающие с формулой (6).

Интересен вопрос – а какая горизонтальная сила, действующая на тело, увеличивает его скорость? Отвечаем – чтобы вставать строго вертикально человек должен действовать с некоторой горизонтальной силой на качели, их ответная реакция и приводит к появлению ускорения тела в горизонтальном направлении^[2].

Теперь с помощью закона сохранения энергии

(~mg (l – h) (1 – cos varphi_1) = frac{m upsilon^2_1}{2} = frac{m upsilon^2_0}{2} left(frac{l}{l-h} right)^2 = mgl (1 – cos varphi_0) left(frac{l}{l-h} right)^2) (10)

можно найти максимальный угол отклонения качелей φ₁ в противоположном направлении (Рис. 242в), который удовлетворяет условию

(~(1 – cos varphi_1) = (1 – cos varphi_0) left(frac{l}{l-h} right)^3) . (11)

Ясно, что этот угол больше начального. Далее в верхней точке человек должен быстро присесть, что бы опять подняться в нижней точке. Если человек будет приседать в верхней точке, где скорость качелей равна нулю, то на основании закона сохранения импульса (также как и на основании энергетического баланса) потерь энергии колебаний не произойдет! Если же приседать в другой точке траектории, то скорость колебаний уменьшится, что и является причиной потерь механической энергии. Таким образом, за половину периода колебаний угол отклонения качелей увеличился, и при этом тело вернулось в исходное нижнее положение относительно качелей. Оценим также изменение высоты подъема за этот промежуток времени

(~Delta z = l(1 – cos varphi_1) – l(1 – cos varphi_0) = l left(left(frac{l}{l-h} right)^3 – right) approx 3l frac{h}{l}) . (12)

Легко показать, что соответствующее увеличение потенциальной энергии равно работе, совершенной при вставании. В проведенном расчете мы пренебрегли силами трения в оси вращения качелей и сопротивлением воздуха. Понятно, что в установившемся режиме, рассмотренный механизм «подкачки» энергии (совершение работы при вставании) восполняет потери механической энергии.

Можно подвести некоторые итоги. Мы показали, что периодическое изменение параметров системы может приводить к возникновению и поддержанию незатухающих параметрических колебаний в колебательных системах с трением и другими силами сопротивления. При этом потери механической энергии компенсируются работой сил, изменяющих параметры системы. На примере рассмотренного движения качелей видно, что их максимальное раскачивание достигается в том случае, когда частота изменения параметра в два раза превышает собственную частоту колебаний системы – за один период нужно дважды приседать и дважды вставать.

Это правило является общим и для других систем, в которых совершаются параметрические колебания. Такое возрастание амплитуды колебаний называется параметрическим резонансом. Главное его отличие от резонанса при вынужденных колебаниях заключается в том, что он наступает в том случае, когда частота изменения параметров системы в два раза превышает собственную частоту колебаний.

В отличие от вынужденных колебаний, параметрические не являются самовозбуждающимися – необходимо некоторое начальное отклонение системы от положения равновесия, что начался процесс параметрических колебаний. Посмотрите на проведенные выкладки для описания колебаний качелей, при отсутствии начального угла отклонения – появление колебаний невозможно.

В заключение данного раздела отметим, что параметрические колебаний возможны и других колебательных системах, электрических, оптических и т.д.

Примечания

1. ↑ Это уравнение широко известно, оно даже имеет персональное имя – уравнение Матье. К сожалению, оно не имеет аналитического решения, выражаемого через элементарные функции, поэтому его решают либо приближенными методами, либо численно, с помощью компьютера.
2. ↑ Если рассматривать движение тела во вращающейся неинерциальной системе отсчета, то эта сила называется силой Кориолиса, это та же сила, что подмывает берега рек из-за вращения Земли.

Следующая страница