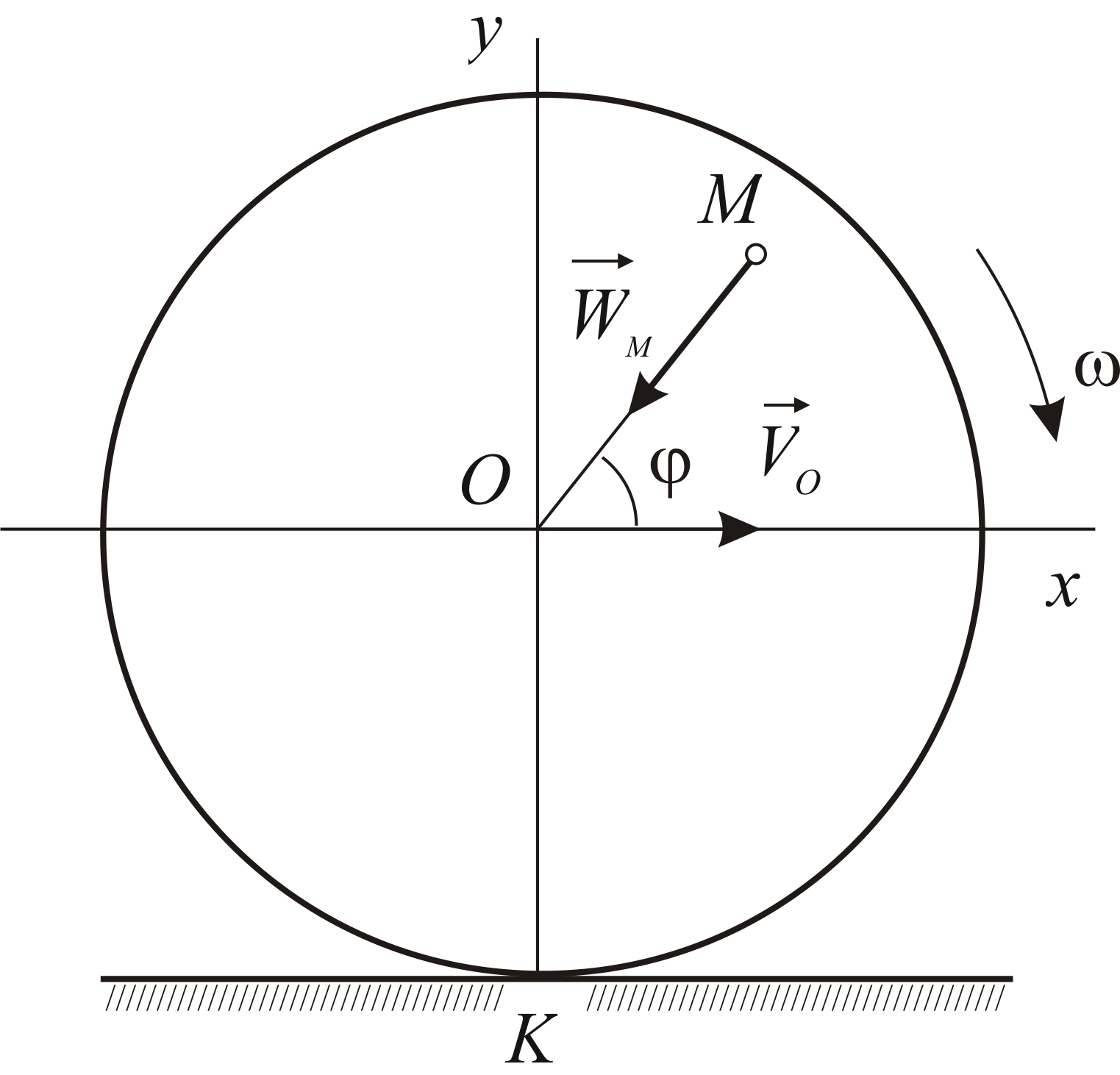
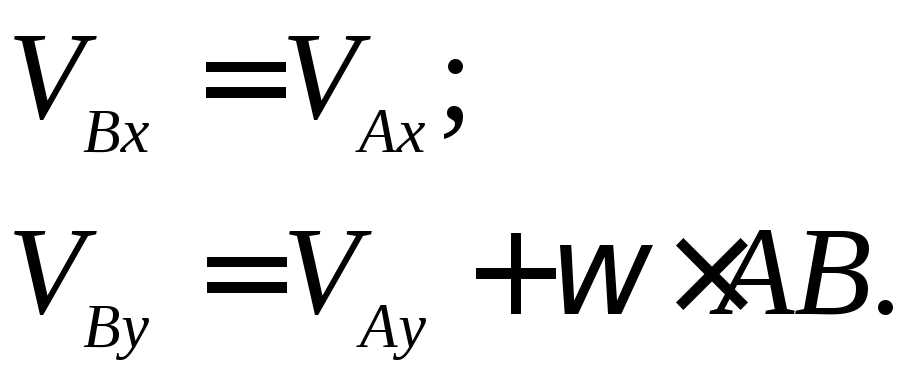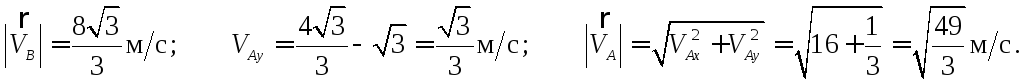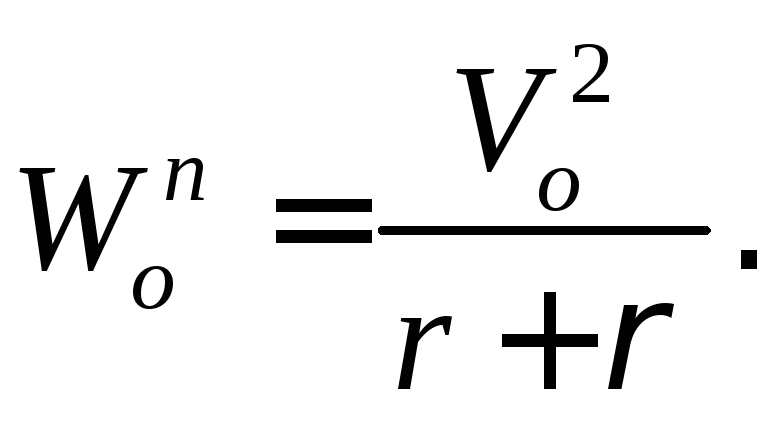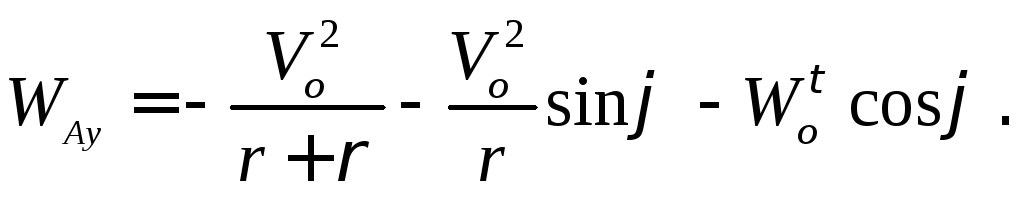Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Расчет скорости колеса
Скорость колеса – это физическая величина, характеризующая скорость, с которой точка движется по окружности вокруг центра вращения.
Формула расчета скорости колеса:
V = 2 * π * R * n, где
V – линейная скорость;
R – радиус окружности;
n – угловая скорость.
Смотрите также перевод угловой скорости в линейную и наоборот – об/мин в м/с.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор для расчета скорости колеса по простой математической формуле в зависимости от скорости вращения и радиуса колеса. С помощью этой программы вы в один клик сможете рассчитать скорость колеса.
Угловая и линейная скорость
Переход от угловой к линейной скорости.
Сегодня смотрел на детей, катающихся на карусели, и подумал — а интересно, с какой скоростью они крутятся.
Подумав еще, понял, что ответить на этот вопрос очень просто, достаточно подсчитать, сколько оборотов в минуту они совершают.
Зная число оборотов в минуту, можно найти угловую скорость в радианах в секунду — за один оборот угол меняется на радиан, за минуту – радиан, и соответственно за секунду — радиан.
Это угловая скорость — радиан/сек. Переход к линейной тривиален — углу в 1 радиан соответствует дуга окружности равная радиусу, соответственно,
Вот и все, а ниже калькулятор. Скорость в м/с приводит к км/час, чтобы было понятнее.
Парадокс колеса
На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.
В то же время из школьного курса математики известно, что длина окружности равна:
Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.
Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:
C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.
Но на самом деле она проходит фактически путь вдвое больший.
Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.
Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.
Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.
Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.
Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:
V = w*R, где w – угловая скорость вращения колеса.
Фактически линейная скорость внутренних точек колеса должна описываться уравнением:
V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.
Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.
Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.
Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:
dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R
Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.
С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.
Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.
[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.
Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.
Сазонов Сергей 3 сентября 2019 года в 12:54
Писать рецензию на Вашу бредятину “Парадокс колеса” считаю излишним (много чести) – найдите в детском журнале “Квант” за 1975 год статью “ЦИКЛОИДА” . Там – примерно этот круг вопросов. Парадокса нет.
(конец цитаты)
К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.
[spoiler title=”источники:”]
http://planetcalc.ru/556/
http://proza.ru/2019/09/02/1746
[/spoiler]
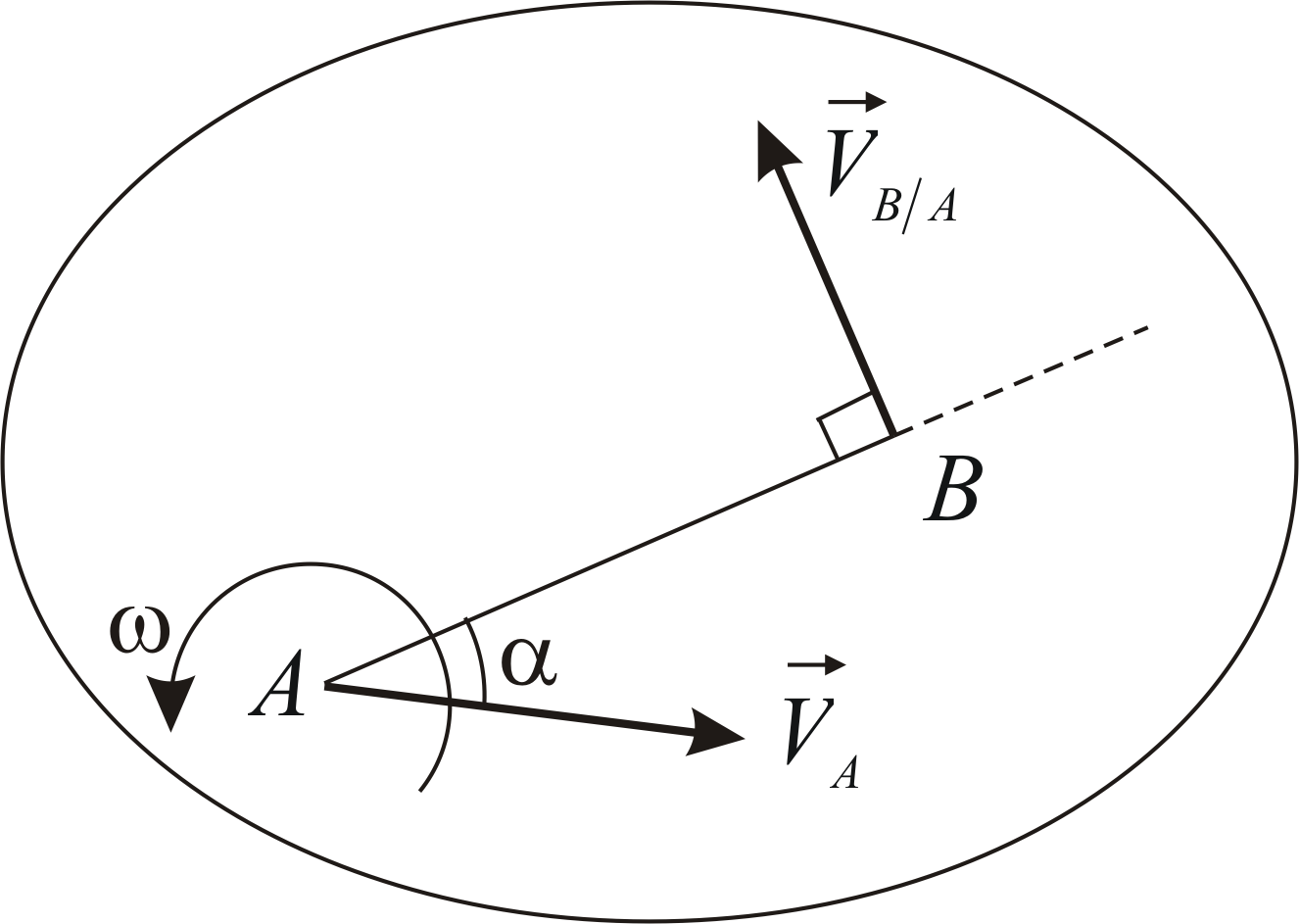
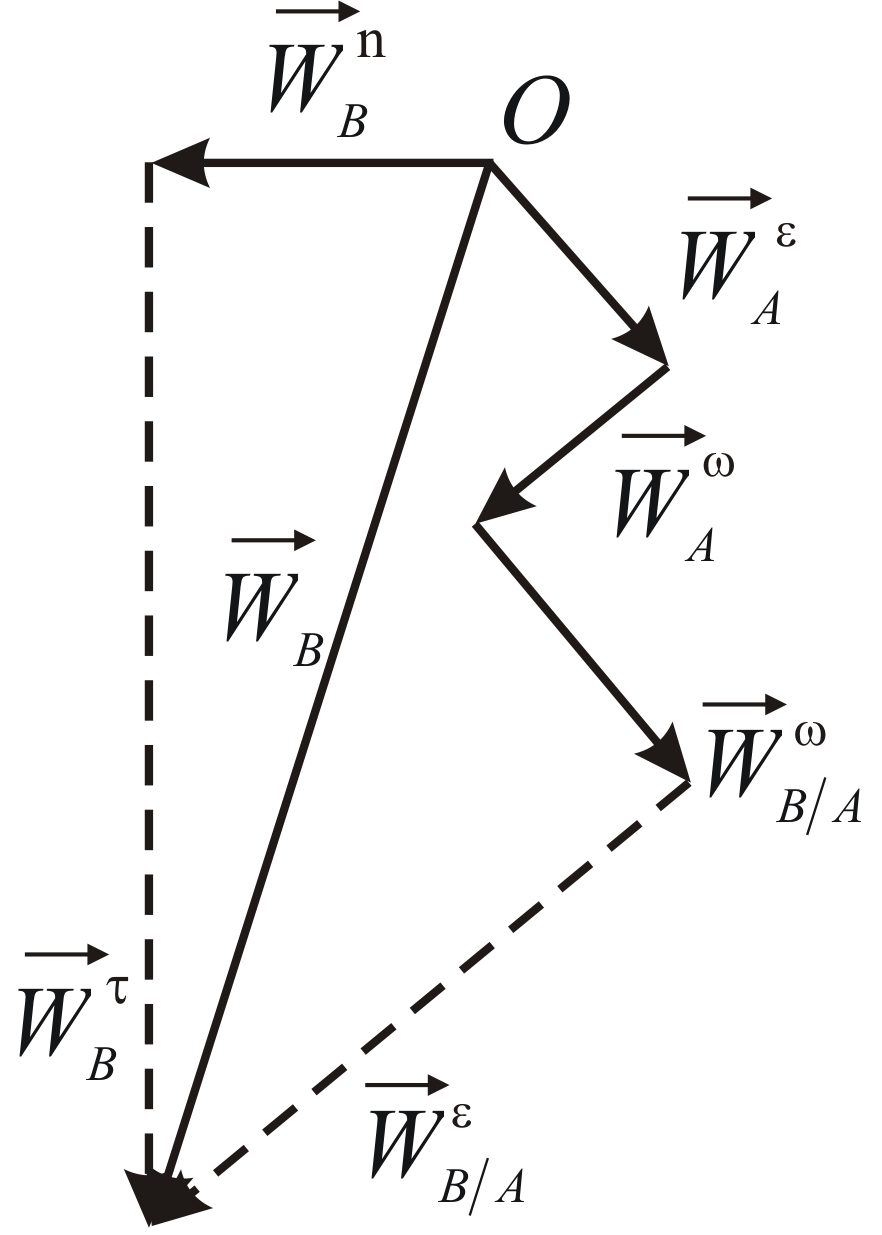
В любой момент времени скорости
любых двух точек плоской фигуры
и
связаны равенством
|
|
|
Рис. 2.3 |
(a)
Вектор
представляет собой скорость, полученную
точкойпри вращении плоской фигуры вокруг оси,
проходящей через полюсперпендикулярно плоской фигуре. Этот
вектор направлен перпендикулярно
отрезку(по касательной к окружности, которую
описывает точкапри вращении тела вокруг оси
),
причем в сторону вращения тела (Рис.
2.3). В соответствии с формулой Эйлера
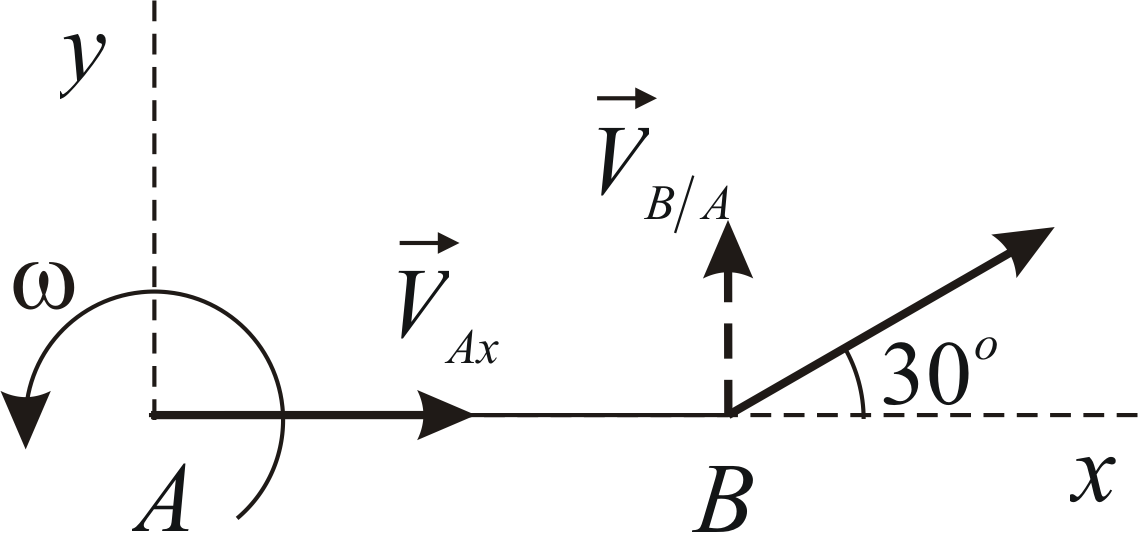
Пример 2.4
Пластина совершает плоскопараллельное
движение. В данный момент времени угловая
скорость пластины равна
,
проекция на осьскорости точки
пластины равна
.
Скорость точкиобразует с осью
угол
(Рис. 2.4). Определить модули скоростей
точеки
,
если.
|
|
|
Рис. 2.4 |
Запишем уравнение (a)
в проекциях на координатные оси:
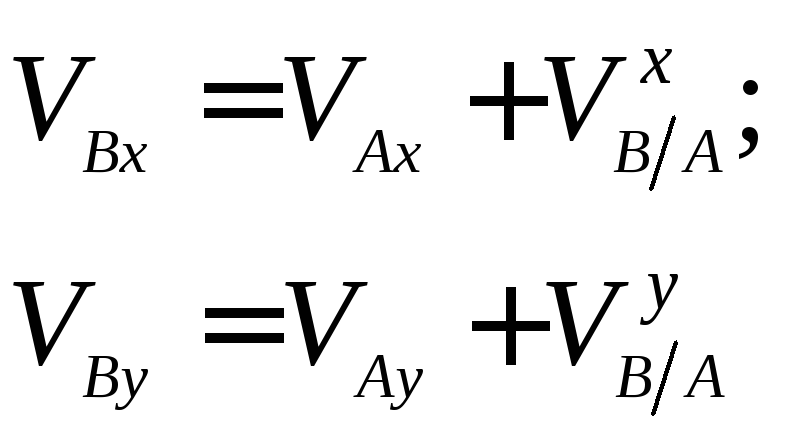
Учитывая данные задачи, получаем:

Отсюда:
Следует заметить, что прямое
использование формулы (a)
целесообразно в довольно небольшом
числе случаев. В некоторых задачах имеет
смысл использовать так называемую
теорему о проекциях. Поскольку векторперпендикулярен отрезку
,
из формулы (a) получаем
утверждение:
проекции скоростей концов отрезка,
соединяющего две точки абсолютно
твердого тела, на направление этого
отрезка равны.
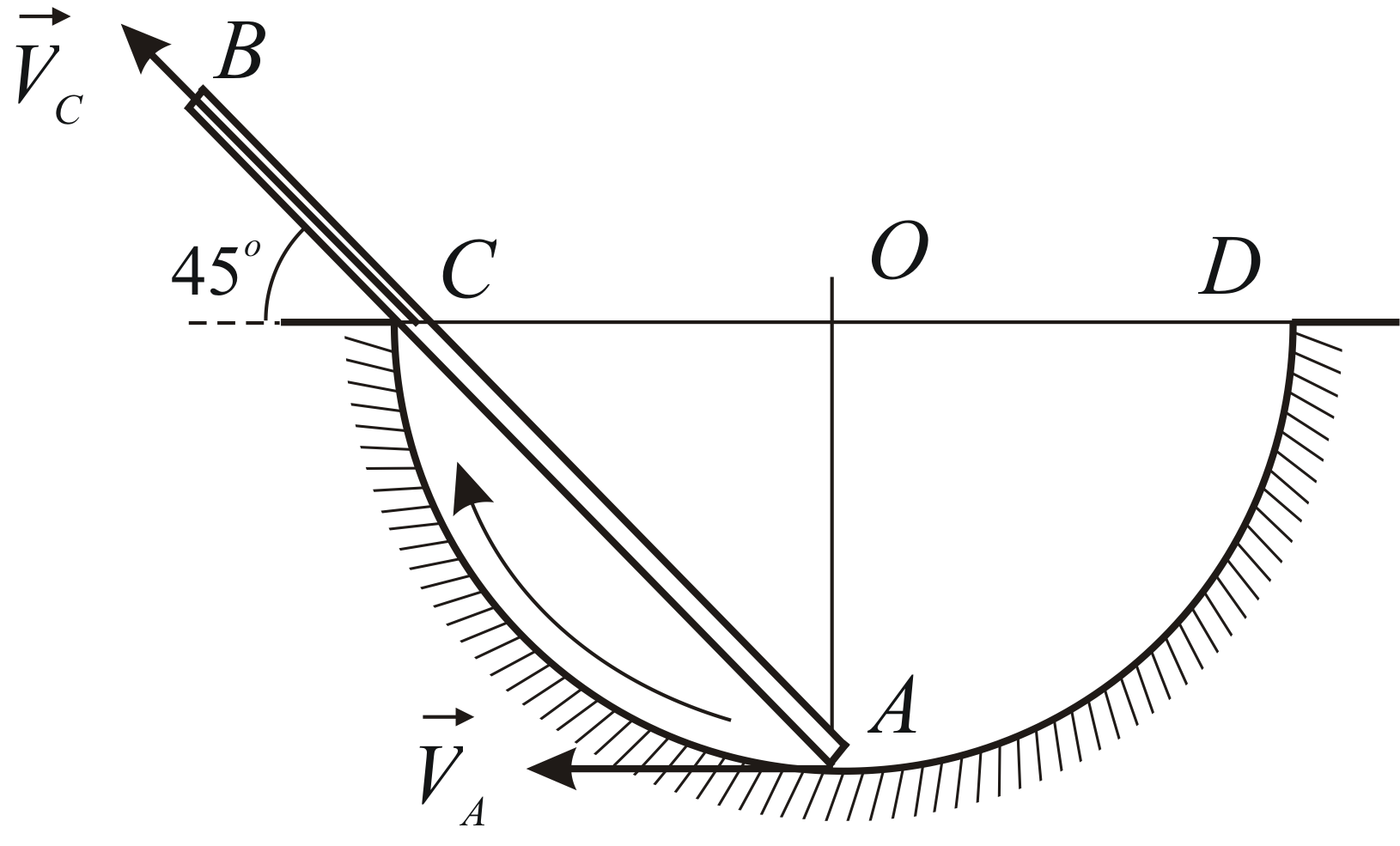
Пример 2.5
Стержень
движется в плоскости рисунка, причём
его конецвсё время находится на полуокружности
,
а сам стержень всё время касается
неподвижного выступа,
расположенного на диаметре(Рис. 2.5). Определить скорость
точки стержня, касающейся выступа, в
тот момент времени, когда радиусперпендикулярен
,
если известно, что скорость точкив этот момент
.
|
|
|
Рис. 2.5 |
Заметим, что направления скоростей
точеки
в данный момент времени известны.
Скорость точкинаправлена по касательной к траектории,
т.е. по касательной к окружности в нижней
точке. Скорость точкинаправлена вдоль стержня, т.к. по условию
задачи стержень не отрывается от выступа.
Таким образом, для заданного положения
стержня известны углы, которые образуют
векторы скоростей точеки
с отрезком
.
В таком случае целесообразно использовать
теорему о проекциях скоростей:
Решение задач с помощью мгновенного
центра скоростей. Основной способ
определения поля скоростей при
плоскопараллельном движении твёрдого
тела основан на использовании мгновенного
центра скоростей.
Как уже говорилось, за полюс можно
принять любую точку плоской фигуры. В
данный момент времени различные точки
тела имеют разные скорости. За полюс
имеет смысл принимать точку, скорость
которой в данный момент времени равна
нулю.
Точка, принадлежащая плоской фигуре
или неизменно с ней связанная, скорость
которой в данный момент времени равна
нулю, называется мгновенным центром
скоростей.
|
|
|
Рис. 2.6 |
Скорость любой точкиплоской фигуры определяется так же, как
если бы тело вращалось вокруг оси,
проходящей через мгновенный центр
скоростей перпендикулярно плоскости
движения плоской фигуры (Рис. 2.6):
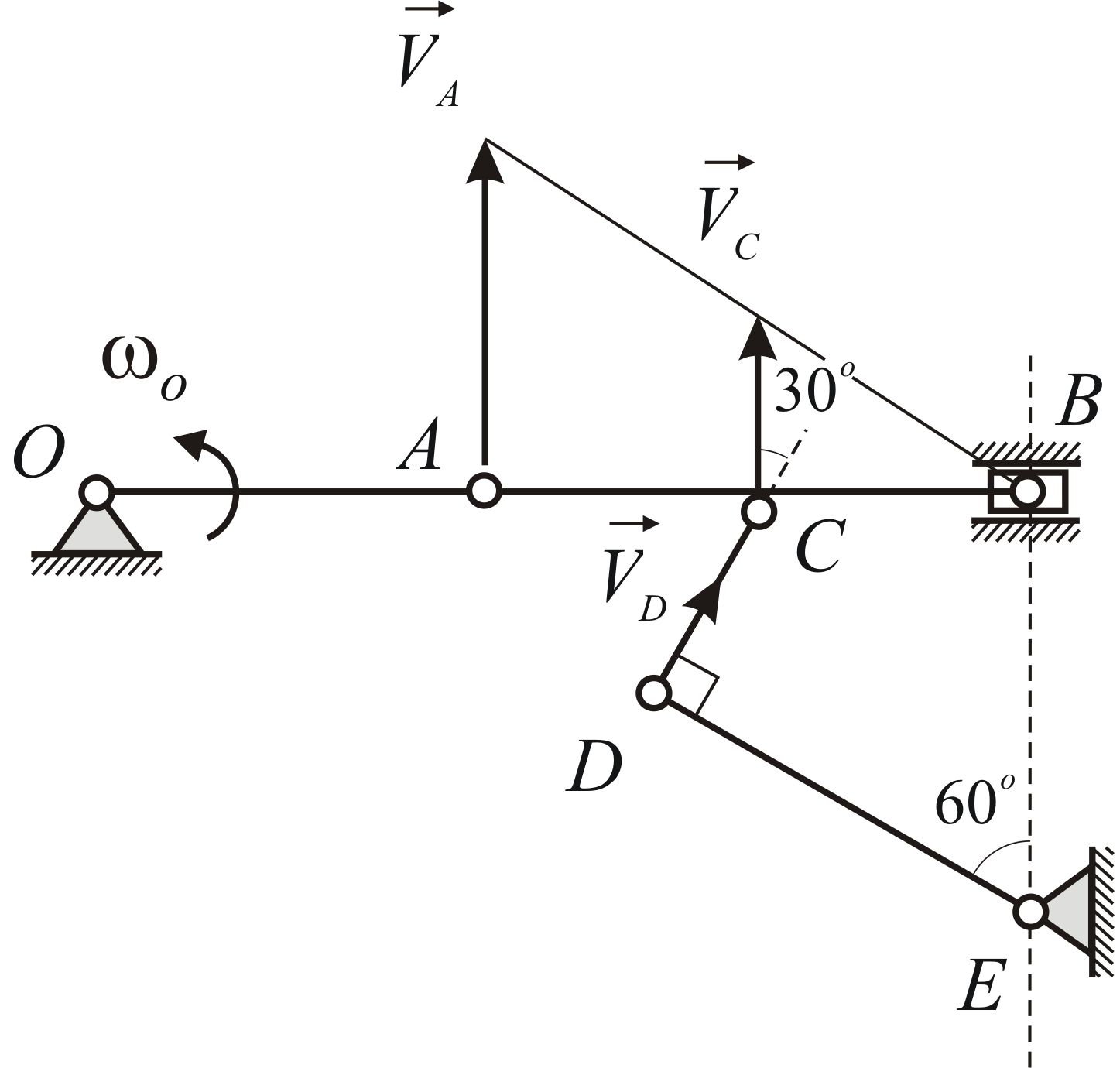
Пример 2.6
Кривошипн0-шатунный механизм связан
шарнирно в середине
шатуна со стержнем
,
а последний – со стержнем,
который может вращаться вокруг оси.
Определить угловую скорость стержняв указанном на Рис. 2.7 положении механизма,
если точкии
расположены на одной вертикали; угловая
скоростькривошипа
равна 8 рад/с,
|
|
|
Рис. 2.7 |
Стерженьвращается вокруг неподвижной оси.
Скорость точкиопределяем по формуле Эйлера:
Движение стержня
плоскопараллельное. Мгновенный центр
скоростей находится в точке.
Учитывая, что скорости точек тела
пропорциональны расстояниям до
мгновенного центра скоростей, получаем:
Отсюда:
Движение стержня
плоскопараллельное. Скорость точки
направлена по касательной к окружности
радиуса,
которая является траекторией точки.
При заданном положении механизма
направление скорости точкисовпадает с направлением стержня
.
Для определения скорости точкиимеет смысл использовать теорему о
проекциях скоростей:
Остаётся определить угловую скорость
стержня
.
Поскольку движение этого стержня
вращательное, используем формулу Эйлера:
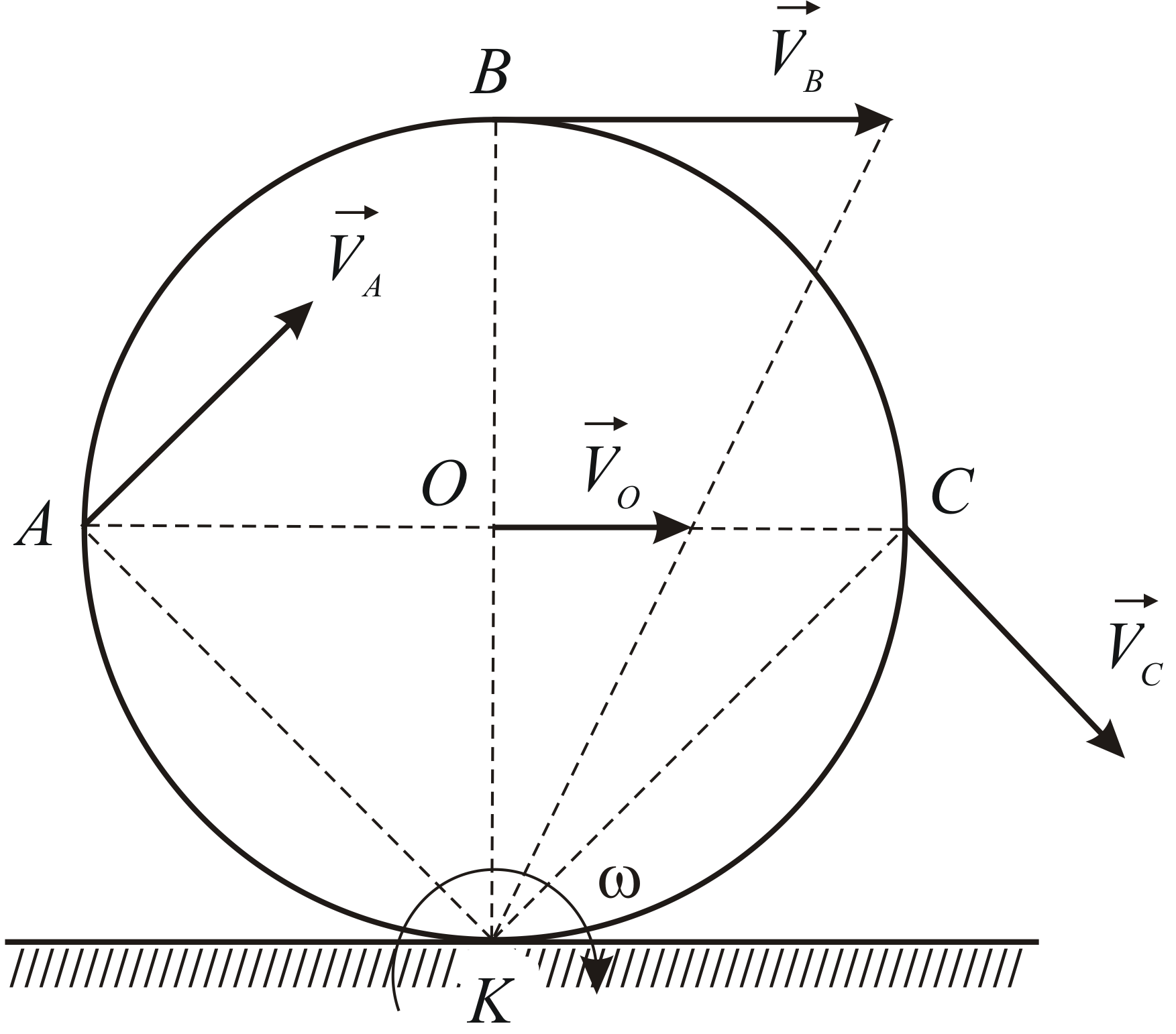
Пример 2.7
Колесо радиуса
катится без скольжения по неподвижной
поверхности (Рис. 2.8). Скорость центра
колеса.
Определить скорости точеки
|
|
|
Рис. 2.8 |
Мгновенный центр скоростейнаходится в точке касания колеса и
дороги. Зная скорость центра, находим
угловую скорость колеса:
Скорости точек колеса определяем по
формуле Эйлера:
Качение колеса представляет интерес
еще и в том отношении, что позволяет
проиллюстрировать смысл формулы (a).
Пусть колесо, движение которого мы
рассматриваем, – ведущее колесо, т.е.
оно принудительно вращается некоторым
приводом. Рассмотрим возможные
режимы движения.
Может случиться так, что колесо
вращается, но автомобиль не перемещается
– буксует. В этом случае движение колеса
представляет собой вращение вокруг
неподвижной оси
.
Все точки колеса будут описывать
окружности с центром в точке,
радиусы которых равны расстояниям от
этих точек до оси колеса. Скорость любой
точки направлена по касательной к этой
окружности и определяется по формуле
Эйлера.
Другое возможное движение колеса
представляет собой качение с
проскальзыванием. Автомобиль при этом
перемещается, но колеса вращаются
несоразмерно быстро. Скорость оси колеса
отлична от нуля и вступает в свои права
формула (a). Скорость,
например, точки,
которая в первом случае была ее полной
скоростью, становится скоростью,
полученной точкойпри вращении колеса вокруг оси
.
Полная же скорость точкитеперь геометрически складывается из
скорости точкии скорости, полученной точкой
при вращении колеса вокруг оси
Заметим, что в этом случае движение
оси (т.е. автомобиля) и вращение колеса
происходят независимо друг от друга и
каждое из них должно быть задано.
Последний режим движения колеса –
качение без скольжения. Именно этот
случай рассмотрен в примере 2.7. Движение
оси и вращение колеса оказываются
взаимосвязанными. В каждое мгновение
очевидно положение точки, скорость
которой равна нулю. В такой ситуации
при определении скоростей точек колеса
удобнее за полюс брать не точку
,
а мгновенный центр скоростей.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 16.3;
16.10; 16.15; 16.16; 16.19; 16.24; 16.28; 16.29; 16.31;
16.32; 16.33; 16.34; 16.35; 16.36; 16.38; 16.39.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплект СР-20.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6
Пример 2.8
Определить скорость и ускорение ползуна
кривошипного механизма, а также угловую
скорость и угловое ускорение шатунав положении, изображенном на Рис. 2.9.
Кривошипвращается замедленно, имея в данный
момент времени угловую скоростьи угловое ускорение
.
Ползун движется по криволинейной
направляющей, имеющей в данном положении
механизма радиус кривизны.
Дано:.
Зная направления скоростей точек
и
,
построим мгновенный центр скоростейстержня
,
после чего определим угловую скорость
стержня
и скорость точки
Попытка определить угловое ускорение
стержня
,
используя определение
закончится неудачей, поскольку зависимость
неизвестна.
Для определения ускорения точки
принимаем за полюс точку
.
Поскольку известны траектории всех
точек во всех их движениях, представим
ускорения точек их составляющими:
Вычислим векторы, входящие в уравнение
.
|
|
|
Рис. 2.9 |
Точка
принадлежит вращающемуся телу
.
Определяем модули составляющих ускорения
этой точки:
направления векторов показаны на
Рис. 2.9.
Точка
движется по криволинейной направляющей.
Касательное и нормальное ускорения
точкиопределяются по формулам:
направления составляющих ускорения
показаны на Рис. 2.9. По приведенной
формуле не удается вычислить касательное
ускорение точки
,
поскольку неизвестны зависимости
расстоянийи
от времени.
Находим составляющие ускорения,
полученного точкой
при вращении шатуна
вокруг оси
.
Заметим, что вращательное ускорение
остается неизвестным по модулю, поскольку
неизвестно угловое ускорение шатуна:
Таким образом, из шести векторов,
входящих в равенство
,
только два неизвестны по модулю. Определим
эти неизвестные из уравнения.
Это уравнение можно решить аналитически
или геометрически. Рассмотрим оба
способа решения.
Имеет смысл выбрать координатные
оси так, чтобы в каждое уравнение в
проекциях входила только одна неизвестная.
Направим ось
вдоль
(перпендикулярно
),
а осьпо направлению
(перпендикулярно
).
Записывая уравнениев проекциях на ось
,
получаем:
Отсюда
Отрицательный знак говорит о том,
что предполагаемое направление вектора
было выбрано ошибочно; в действительности
этот вектор направлен в противоположную
сторону.
Записывая уравнение
в проекциях на ось
,
получаем:
Отсюда
|
|
|
Рис. 2.10 |
Вычислив,
можем определить угловое ускорение
стержня:
Рассмотрим геометрический способ
решения уравнения
.
Построим в масштабе сумму векторов,
стоящих в правой части уравнения.
От некоторой точкиотложим
,
от его конца отложим,
а затем(Рис. 2.10). Остается построить
,
модуль которого неизвестен. Проведем
через конецпунктирную прямую, параллельную
.
Конец суммы векторов, стоящих в правой
части уравнения,
лежит на этой прямой.
Обратимся к левой части уравнения
.
Отложим от точкиизвестный вектор
.
Через его конец проведем пунктирную
прямую, параллельную вектору.
Точка пересечения построенных прямых
определяет положение конца вектора
ускорения точки.
Пример 2.9
Колесо радиуса
катится без скольжения по прямолинейному
пути (Рис. 2.11). Ось колеса движется
ускоренно, имея в данный момент времени
скоростьи ускорение
.
Определить проекции ускорение любой
точкиобода колеса на оси координат.
Принимая за полюс точку
,
получаем:
причем
где
– угловая скорость колеса;
– его угловое ускорение.
|
|
|
Рис. 2.11 |
Зная положение мгновенного
центра скоростей колеса – точка касания
колеса и дороги, определяем угловую
скорость колеса:
В рассматриваемой задаче расстояние
от точки
,
скорость которой известна, до мгновенного
центра скоростейсо временем не изменяется. Это
обстоятельство позволяет найти угловое
ускорение колеса в данный момент времени
по определению углового ускорения:
,
так как
представляет собой проекцию вектора
ускорения точкина направление её вектора скорости,
которая в рассматриваемом случае равна.
Записывая уравнение
в проекциях на координатные оси, получаем
проекции вектора ускорения точки:
Пример 2.10
Колесо радиуса
катится без скольжения по криволинейной
поверхности (Рис.2.12). Ось колеса движется
ускоренно, имея в данный момент времени
скоростьи касательное ускорение
.
Определить проекции ускорения любой
точкиобода колеса на заданные координатные
оси, если радиус кривизны в точкеравен
.
|
|
|
Рис. 2.12 |
Задача решается так же, как в
примере 2.9, но в отличие от предыдущей
задачи, траектория точки– кривая линия. У точки
появляется вторая составляющая ускорения
– нормальная:
В результате получаем:
Пример 2.11
Колесо радиуса
катится без проскальзывания по
прямолинейному пути. Ось колеса движется
равномерно со скоростью(Рис. 2.13). Определить ускорение любой
точкиколеса.
|
|
|
Рис. 2.13 |
Ось колеса движется равномерно
и прямолинейно. Следовательно, точка– мгновенный центр ускорений. Для любой
точкиколеса получаем:
Но угловая скорость колеса
постоянна и, следовательно, угловое
ускорение колеса равно нулю.
Тогда
Таким образом, ускорение любой точки
совпадает с осестремительным ускорением,
полученным этой точкой при вращении
колеса вокруг оси, проходящей через
центр колеса
перпендикулярно плоскости движения.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 18.11;
18.13; 18.16; 18.18; 18.22; 18.23; 18.25; 18.26;
18.28; 18.37; 18.38; 18.39; 18.40.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-21;
СР-22.
ПРАКТИЧЕСКИЕ
ЗАНЯТИЯ № 7-8
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2015560.03 Кб15PSY – recommendation.pdf
- #
- #
Линейная скорость через угловую, теория и онлайн калькуляторы
Линейная скорость через угловую
Определение
Мгновенной (истинной) скоростью ($overline{v}$) называют векторную физическую величину, равную производной от вектора перемещения по времени ($t$):
[overline{v}={mathop{lim }_{Delta tto 0} frac{Delta overline{r}}{Delta t}=frac{doverline{r}}{dt} }left(1right).]
$Delta overline{r}$- вектор перемещения материальной точки, это перемещение точка совершает за отрезок времени $Delta t$.
Выражение линейной скорости через угловую скорость
Скорость называют мгновенной, так как ее значение показывает величину скорости в определенный момент времени.
Так как вектор перемещения $Delta overline{r}$ направлен по хорде, которая соединяет две близкие точки криволинейной траектории движения частицы, при уменьшении расстояния между этими точками, вектор $Delta overline{r}$ занимает положение касательной к линии, по которой движется частица. Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.
Скорость прохождения пути ($s$) определяют:
[v={mathop{lim }_{Delta tto 0} frac{Delta s}{Delta t}=frac{ds}{dt}left(2right). }]
Мгновенную скорость называют линейной тогда, когда хотят подчеркнуть ее отличие от угловой скорости.
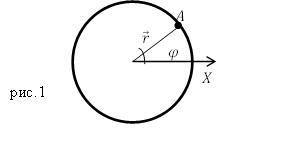
Если материальная точка движется по окружности, то ее положение характеризуют при помощи угла поворота ($varphi $), который образует радиус-вектор ($overline{r}$), определяющий положение рассматриваемой точки А с выделенным неизменным направлением от которого производят отсчет (рис.1).
Быстроту изменения угла поворота $varphi $ характеризуют при помощи такой физической величины как угловая скорость. Обычно угловую скорость обозначают буквой $omega $. Угловая скорость равна:
[omega =frac{dvarphi }{dt}left(3right).]
Вращение называют равномерным, если угловая скорость постоянна $omega =const$. При равномерном вращении $omega $ можно называть угловой частотой.
Линейная скорость движения точки по окружности связана с угловой скоростью. Пусть точка проходит путь равный длине дуги XA (рис.1). Этот путь обозначим $s$. Если радиус окружности равен$ R=const$, то длину дуги найдем как:
[s=Rvarphi left(4right).]
Продифференцируем обе части выражения (4) по времени, имеем:
[frac{ds}{dt}=frac{dleft(Rvarphi right)}{dt}=Rfrac{dvarphi }{dt}left(5right).]
Мы видим, что в левой части получена величина линейной скорости, в правой части радиус окружности умножен на угловую скорость:
[v=Romega left(6right).]
Формула (6) будет справедлива при движении точки по криволинейной траектории отличной от окружности, но в этом случае $R$ – радиус кривизны траектории в месте нахождения частицы.
В векторном виде выражение (6) записывают так:
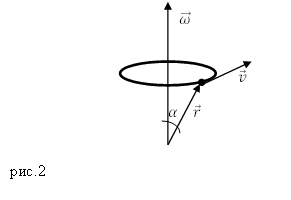
[overline{v}=overline{omega }times overline{r}left(7right),]
$overline{r}$ – вектор, соединяющий ось вращения и движущуюся точку (рис.2). Модуль скорости, используя формулу (7) найдем как:
[v=omega r{sin alpha left(8right), }]
где $alpha $ – угол между вектором угловой скорости и $overline{r}.$
Угловая скорость через линейную
Исходя из приведенных выше формул угловую скорость можно выразить через линейную. При движении по окружности:
[omega =frac{v}{R}left(9right).]
Или используя формулу (8) угловую скорость выразим как:
[omega =frac{v}{r{sin alpha }}left(10right).]
Примеры задач с решением
Пример 1
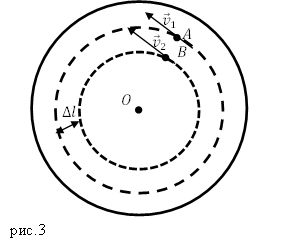
Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($omega $)?
Решение. Основой для решения задачи будет формула:
[omega =frac{v}{R}left(1.1right).]
Угловые скорости движения точки A и B одинаковы (${omega }_A={omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1):
[{omega }_A=frac{v_1}{R_1};; {omega }_B=frac{v_2}{R_2}left(1.2right).]
$R_1$ – расстояние от точки O до точки A; $R_2=R_1-Delta l$ – расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$:
[frac{v_1}{R_1}=frac{v_2}{R_1-Delta l}to R_1=frac{Delta lcdot v_1}{v_1-v_2}left(1.3right).]
Найдем угловую скорость точки A:
[{omega }_A=v_1cdot frac{v_1-v_2}{Delta lcdot v_1}=frac{v_1-v_2}{Delta l}.]
Ответ. Угловая скорость всех точек диска равна $omega =frac{v_1-v_2}{Delta l}$
Пример 2
Задание. Колесо радиусом R=1 м вращается так, что угол поворота изменяется в соответствии с
законом: $varphi left(tright)=2+5t^3(рад)$. Определите, какова линейная скорость точек обода колеса в момент времени,
равный $t’=1 (с)$.
Решение. В качестве основы для решения задачи воспользуемся формулой:
[v=Romega left(2.1right).]
Используя уравнение $varphi left(tright)$ и связь угла поворота и угловой скорости найдем $omega $:
[omega =frac{dvarphi }{dt}=frac{d}{dt}left(A+Bt^3right)=3Bt^2(2.2).]
Подставим результат (2.2) в (2.1), имеем:
[v=Rcdot 3Bt^2.]
Вычислим искомую скорость:
[v=1cdot 3cdot 5cdot 1^2=15 left(frac{м}{с}right).]
Ответ. $vleft(t’right)=15frac{м}{с}$
Читать дальше: масса и плотность вещества.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.