Что такое линейная скорость, единицы измерения
Определение
Скоростью при равномерном движении тела называют физическую величину, с помощью которой определяют путь, преодоленный телом за единицу времени.
В международной системе СИ единицей измерения линейной скорости является производная от двух основных единиц:
- метр;
- секунда.
В международной системе СИ скорость измеряется в метрах в секунду (м/с). За единицу скорости принимают скорость равномерного движения, при которой путь в один метр тело преодолеет в течение одной секунды. Кроме того, скорость можно измерять в:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- км/ч;
- км/с;
- см/с.
Связь между линейной и угловой скоростями
Скорость точки, которая совершает круговое движение, называется линейной скоростью, чтобы отделить это понятие от термина угловая скорость. Во время вращения абсолютно твердое тело в разных точках будет обладать неодинаковыми линейными скоростями, но значение угловой скорости остается стабильным.
Можно установить связь между линейной и угловой скоростью тела, вращающегося по окружности. Путь, который проходит точка, расположенная на окружности с радиусом R, составляет:
2πR
Исходя из того, что время одного оборота тела является периодом Т, модуль линейной скорости будет рассчитан по следующей формуле:
(v=frac{2pi R}{T}=2pi RV)
Зная, что:
(omega =2pi V)
получим справедливое равенство:
(v=omega R)
Данная формула демонстрирует увеличение линейной скорости тела при его удалении от оси вращения. К примеру, точки, которые движутся по земному экватору v=463 м/с, а точки, расположенные на широте города Санкт-Петербург, движутся со скоростью v=233 м/с. При нахождении на полюсах планеты скорость уменьшается до v=0.
Модуль центростремительного ускорения точки тела, которая совершает равномерные вращательные движения, определяют с помощью угловой скорости тела и радиуса окружности. Уравнение будет записано в следующем виде:
(a=frac{v^{2}}{R})
(v=omega R)
Таким образом, формула будет преобразована:
(a=omega ^{2}R)
Подытожив расчеты, можно записать все возможные равенства, справедливые для определения центростремительного ускорения:
(a=frac{v^{2}}{R}=omega ^{2}R=frac{4pi ^{2}}{T^{2}}R=4pi ^{2}V^{2}R)
Таким образом, рассматривают пару простейших движений, характерных для абсолютно твердого тела, включая поступательное и вращательное. При этом стоит отметить, что определить любое сложное движение, которое совершает абсолютно твердое тело, можно с помощью суммы двух независимых движений:
- поступательное;
- вращательное.
С помощью закона независимости движений описывают сложное движение абсолютно твердого тела.
Формулы для нахождения линейной скорости
Тело движется равномерно тогда, когда его скорость характеризуется постоянной величиной. Формула для расчета скорости такого движения будет иметь следующий вид:
V = st
где s является пройденным путем, то есть длиной линии;
t представляет собой время, в течение которого тело преодолевало указанный путь.
Определение
Линейной скоростью V называют физическую величину, которая демонстрирует путь, пройденный телом в течение определенного времени.
Основной формулой для определения линейной скорости является следующее равенство:
V = St
где S является путем,
t обозначает время, в течение которого тело преодолело путь S.
Иной вариант уравнения имеет такой вид:
V = lt
где l является путем,
t обозначает время, в течение которого тело преодолело дугу l.
В некоторых научных источниках скорость обозначают с помощью маленькой буквы v. Другим уравнением для расчета линейной скорости является равенство:
(v=2pi RT)
В данном случае 2π представляет собой полную окружность и составляет 360 угловых градусов. Вектор скорости направлен по касательной к траектории движении тела.
Модуль скорости
Числовое значение скорости может быть разным в зависимости от выбранной единицы измерения. Кроме числового значения, скорость характеризуется направлением. Числовое значение, которым обладает скорость, в физике называют ее модулем.
В случае, когда скорость обладает определенным направлением, такая величина является векторной. Таким образом, скорость представляет собой векторную физическую величину. Записывают модуль скорости в виде буквы v, а вектор скорости, как (vec{v})
Следует отметить, что такие величины, как путь, время, длина обладают только числовым значением. Они называются скалярными. Если тело движется неравномерно, то справедливо использовать в расчетах среднюю скорость.
Задачи с примерами решения
Задача №1
Тело совершает движение по окружности с ускорением 3 м/с в квадрате. Радиус окружности равен 40 метров. Необходимо определить линейную скорость движения тела.
Решение:
Ускорение в данном случае будет нормальным. Исходя из этого, определить линейную скорость тела можно с помощью формулы:
(a=frac{v^{2}}{R})
(v=sqrt{aR}=sqrt{40times 3}=10.9) м/с
Ответ: линейная скорость равна 10,9 м/с.
Задача №2
Поезд совершает равномерное движение. В течение 4 часов он преодолевает путь в 219 километров. Требуется рассчитать скорость движения поезда.
Решение:
Исходя из основной формулы для расчета линейной скорости, получим:
(v=frac{S}{t}=frac{219}{4}=54.75) км/ч
Ответ: скорость движения поезда составит 54.75 км/ч или 15.2 м/с.
Задача №3
Транспортное средство, работая на двигателе внутреннего сгорания, в течение 2,5 часов преодолевает расстояние в 213 километров. Требуется определить скорость движения транспорта.
Решение:
С помощью уравнения расчета скорости можно записать решение задачи:
(v=frac{S}{t}=frac{213}{2,5}=85.2) км/ч
Ответ: Скорость движение транспортного средства составляет 85.2 км/ч или 23.7 м/с.
Интуитивное понятие о скорости мы получаем ещё с детства. Например, глядя в окно или находясь на улице отмечаем про себя, что некоторые из людей идут быстрее, чем другие, а машины на проезжей части движутся быстрее, чем любой из пешеходов. Однако для физики, как науки, такого, бытового понимания о скорости недостаточно, поэтому вводится её точное определение.
Понятие скорости
Скоростью материальной точки (тела) при равномерном движении называется физическая величина, показывающая, какой путь точка (тело), проходит за единицу времени.
Подчеркнём, что речь идёт именно о пути, а не о перемещении. Перемещением называется вектор, соединяющий точку начала и точку конца движения. Его величина равна расстоянию между этими точками. Путь представляет собой длину траектории, по которой происходило движение. Наглядно это можно показать на рисунке.
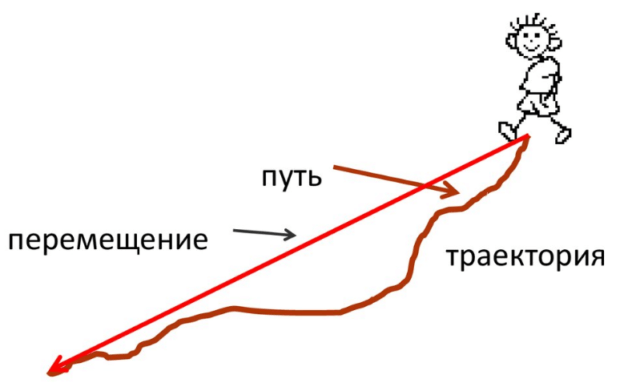
Равномерным движением называют движение, при котором за одинаковые промежутки времени тело проходит одно и то же расстояние. Направление движения при этом может изменяться. В качестве примера можно привести равномерное перемещение точки по окружности.
Формула понятия скорости следующая:
[overline{mathrm{v}}=s / t]
Чёрточка над [overline{mathrm{v}}] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.
Чёрточка над [overline{mathrm{v}}] свидетельство того, что скорость является векторной, т.е. имеющей направление, величиной. Путь s и время t являются скалярными величинами, такими, которые направления в пространстве не имеют.
Из приведённой формулы очень легко найти размерность скорости. Т. к. расстояние измеряется в метрах, а время в секундах, то единицей скорости будет метр в секунду м/с. Отметим, что на практике часто скорость измеряют не в метрах в секунду, а, например, в километрах в час.
Существует ещё так называемая средняя скорость – скалярная величина, равная скорости, с которой бы тело перемещалось, если бы преодолевало путь, двигаясь равномерно.
Примеры
Поезд длиной 300 метров, двигаясь равномерно, проезжает тоннель длиной 420 метров за 3 минуты. Найти скорость поезда.
Решение:
Длину поезда обозначим через l, а длину тоннеля через L.
Словосочетание «проезжает тоннель за 3 минуты» означает, что это время поезд входит в тоннель кабиной машиниста и выходит с концом последнего вагона. Пройденное им расстояние S в таком случае является суммой длины тоннеля и длины поезда.
[S = I + L = 300 + 420 = 720 м/с.]
Скорость поезда – это скорость любой из его точек. Для простоты будем считать, что это скорость кабины машиниста.
Переводим минуты в секунды: 3 * 60 = 180с.
Скорость получаем, разделив перемещение на время: 720/180 = 4 м/с.
Ответ: Скорость поезда равна 4 м/с.
Машина 3 часа едет со скоростью 4 км/ч, затем 4 часа со скоростью 61,2 км/ч. Требуется найти среднюю скорость движения машины на всем её пути.
Решение:
Обозначим время движения машины со скоростью 4 км/ч, как [t_{1}], а время движения машины со скоростью 61,2 км/ч, как [t_{2}].
Находим общий путь, который проехала машина. Обозначим его, как S. Общий равен сумме путей, которые ехала машина со скоростью 58,4 км/ч и 61,2 км/ч. Первый из них обозначим как [S_{1}], он равен [S_{1}] = 3*58,4 = 175,2 км
Второй из них обозначим как S2, он равен: [S_{2} = 4*61,2 = 244,8 км]
Складываем эти расстояния и получаем: S = 175,2 + 244,8 = 420 км
Это есть весь путь, пройденный нашей машиной.
Общее время t, которое она потратила будет [t = t_{1} + t_{2} =3 + 4 = 7 ч]
Чтобы узнать среднюю скорость, делим общее расстояние на общее время v = S/t = 420/7 = 60 км/ч.
Ответ: Средняя скорость машины равна 60 км/ч.
Обращать время в секунды, а скорость в метры в секунду здесь смысла не имеет, можно и так получить нужное решение.
Линейная скорость
Линейной скоростью именуют величину равную пути, проходимым телом за единицу времени. Движение тела при этом может быть как прямолинейным так и совершаться по криволинейной траектории, например, окружности. Отметим, что линейная скорость всегда направлена по касательной к траектории.
Формул для расчета линейной скорости существует множество, но общей можно назвать:
[v=S / t]
S – путь, который прошло тело, t – время, которое оно на это потратило.
Если тело вращается по окружности, то путь, проходимый им, равен её длине. Как известно из геометрии, указанная величина равна 2πR, где R – радиус окружности. Отсюда легко сообразить, что линейная скорость тела при равномерном движении по окружности будет [boldsymbol{v=2 pi R / T}].
Нет времени решать самому?
Наши эксперты помогут!
О связи между линейной и угловой скоростями
Угловой скоростью называется векторная величина, показывающая, насколько быстро и в каком направлении вращается материальная точка или тело относительно центра вращения.
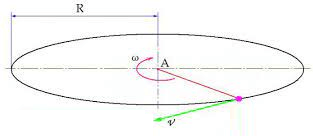
Обозначается она буквой ω. Формула нахождения угловой скорости следующая:
[overline{omega}=phi / t],
где ϕ – угловое перемещение, t – время.
Измеряется угловая скорость в радианах в секунду рад/с.
Теперь о связи между линейной и угловой скоростью. Из формулы[boldsymbol{v=2 pi R / T}] следует, что v также будет равно v = 2πRν, где ν – частота вращения точки. Отсюда легко понять, что v = ωR.
Линейная скорость и ускорение при движении по окружности
Центростремительное ускорение движущейся равномерно по окружности точки вычисляется по формуле:
[a=v^{2} / R]
Оно связывает линейную скорость и ускорение. Исходя из связи линейной и угловой скоростей можно получить:
[a=omega^{2} R]
Сергей Феликсович Савельев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Понятие скорости
Когда мы сравниваем движение каких-либо тел, то говорим, что одни тела двигаются быстрее, а другие – медленнее. Такую простую терминологию мы используем в повседневной жизни, говоря, например, о движении транспорта. В физике быстрота движения тел характеризуется определенной величиной. Эта величина называется скоростью. Общее определение скорости (в случае, если тело движется равномерно):
Определение 1
Скорость при равномерном движении тела – это физическая величина, показывающая, какой путь прошло тело за единицу времени.
Под равномерным движением тела подразумевается, что скорость тела постоянна. Формула нахождения скорости: $v=frac{s}{t}$, $s$ – это пройденный телом путь (то есть длина линии), $t$ – время (то есть промежуток времени, за который пройден путь).
Согласно международной системе СИ, единица измерения линейной скорости является производной от двух основных единиц – метра и секунды, то есть измеряется в метрах в секунду (м/с). Это значит, что под единицей скорости понимается скорость такого равномерного движения, при котором путь в один метр тело проходит за одну секунду.
Также скорость часто измеряют в км/ч, км/с, см/с.
Рассмотрим простой пример задачи на вычисление скорости.
Пример 1
Задача. Двигаясь равномерно, поезд за 4 ч проходит 219 км. Найти его скорость движения.
Решение. $v=frac{219 км}{4 ч}=54,75frac{км}{ч}$. Переведём километры в метры и часы в секунды: $54,75frac{км}{ч}=frac{54750 м}{3600c}approx 15,2frac{м}{c}$.
Ответ. $54,75frac{км}{ч}$ или $15,2frac{м}{c}$.
Из примера мы видим, что числовое значение скорости отличается в зависимости от выбранной единицы измерения.
Кроме числового значения, скорость имеет направление. Числовое значение величины в физике называют модулем. Когда у физической величины есть и направление, то эту величину называют векторной. То есть скорость – это векторная физическая величина.
«Формула для расчета линейной скорости» 👇
На письме модуль скорости обозначается $v$, а вектор скорости – $vec v$.
В свою очередь, такие величины как путь, время, длина и другие характеризуются только числовым значением. Тогда говорят, что это скалярные физические величины.
В случае, когда движение является неравномерным, используют понятие средней скорости. Формула средней скорости: $v_{ср}=frac{s}{t}$, где $s$ – это весь пройденный телом путь, $t$ – всё время движения. Рассмотрим пример задачи на среднюю скорость, чтобы понять разницу.
Пример 2
Задача. Некоторый транспорт за 2,5 часа преодолевает путь в 213 км. Найти его $v_{ср}$.
Решение. $v_{ср}=frac{213 км}{2,5 ч}= 85,2 frac{км}{ч}=frac{213000 м}{9000 с}approx 23,7frac{м}{с} $.
Ответ. $85,2 frac{км}{ч}$ или $23,7frac{м}{с} $.
Линейная скорость
Определение линейной скорости относится к разделу физики о механике и подразделу о кинематике в рамках вопроса движения по окружности. В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость.
Дадим определение линейной скорости.
Определение 2
Линейная скорость $V$ – это физическая величина, показывающая путь, который прошло тело за единицу времени.
Формула линейной скорости:
$V=frac{S}{t}$, где $S$ – путь, $t$ – время, за которое точка прошла путь $S$.
Также существует иной вариант этой формулы:
$V=frac{l}{t}$, где $l$ – путь, $t$ – время, за которое точка прошла по дуге $l$.
В некоторых учебниках линейная скорость также обозначается маленькой буквой $v$.
Есть ещё одна формула, по которой можно найти линейную скорость:
$v=frac{2pi R}{T}$.
$2pi$ соответствует полной окружности (360 угловым градусам).
$vec V$ направленена по касательной к тракетории.
Связь между линейной и угловой скоростями
Чтобы проследить связь между линейной и угловой скоростями, нужно дать определение угловой скорости.
Определение 3
Угловая скорость – это величина, которая равна отношению угла поворота отрезка, соединяющего точку с центром окружности, к промежутку времени, за который этот поворот произошёл.
Записывается эта формула следующим образом:
$omega = frac{phi}{t}$, где $phi$ – это угловое перемещение (или угол поворота, измеряется в радианах), $t$ – промежуток времени, за которое соврешено угловое перемещение.
В системе СИ угловая скорость измеряется в рад/с.
Угловую скорость также называют циклической частотой вращения, потому что при вращении твёрдого тела угловая скорость всех его точек одинакова.
Связь между $V$ и $omega$: $V=omega R$.
Эта формула выводится из определения модуля центростремительного ускорения.
Определение 4
Центростремительное ускорение $a$ – это ускорение точки при равномерном движении по окружности.
$a=frac{V^2}{R}$ и $a=omega^2 R$.
С помощью элементарных математических действий из этих двух формул выводится связь между $V$ и $omega$.
Таким образом, в данной статье мы разобрали следующие понятия:
- скорость;
- линейная и угловая скорость;
- связь между линейной и угловой скоростями.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
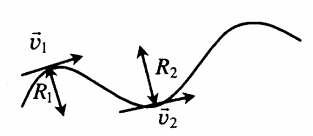
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости
Линейная скорость
Определение и формулы
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
![]()
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость
Определение и формулы
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Полезные факты
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:
![]()
Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:
![]()
Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Определение и формула
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с2). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙103 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙106. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Задание EF18273
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17763
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
- Радиус окружности R1 = R.
- Радиус окружности R2 = 4R.
- Центростремительное ускорение: aц.с. = a1 = a2.
Найти нужно ν2.
Центростремительное ускорение определяется формулой:
![]()
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:
![]()
Или:

Отсюда:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 21.9k
Формула линейной скорости в физике
Формула линейной скорости
Скорость движения тела ($overline{v}$) называют линейной, если хотят подчеркнуть ее отличие от угловой скорости ($omega $). Чаще величину $overline{v}$, являющуюся векторной величиной, основной характеристикой движения тела, называют просто скоростью.
Формула мгновенной скорости
Определение
Мгновенная скорость (обычно просто скорость) – это векторная величина, равная первой производной от радиус-вектора ($overline{r}$), определяющего положение движущейся материальной точки, по времени ($t$):
[overline{v}=frac{doverline{r}}{dt}=dot{overline{r}}left(1right).]
Представим вектор $overline{r}$ в декартовой системе координат в виде:
[overline{r}=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(2right),]
где $overline{i}$; $overline{j}$; $overline{k}$ – единичные орты соответствующих осей координат, постоянные во времени, при этом формулой скорости можно считать выражение:
[overline{v}=overline{i}frac{dx}{dt}+overline{j}frac{dy}{dt}+overline{k}frac{dz}{dt}left(3right).]
Проекциями вектора скорости на оси координат X, Y,Z являются:
[left{ begin{array}{c}
v_x=frac{dx}{dt}, \
v_y=frac{dy}{dt} \
v_z=frac{dz}{dt}. end{array}
right.(4),]
Величину (модуль) скорости найдем в соответствии с формулой:
[v=sqrt{v^2_x+v^2_y{+v}^2_z}.]
Если движение задается при помощи параметров траектории, что означает: известны траектория и функция пути от времени ($s(t)$); путь отсчитывают от точки траектории, которую считают начальной; каждая точка траектории характеризуется своей величиной $s$; радиус – вектор является функцией от $s,$ и траекторию можно задать при помощи уравнения:
[overline{r}=overline{r}left(sright)left(5right),]
в таком случае в формуле (1) $overline{r}left(tright)$ будем рассматривать как сложную функцию: $overline{r}left[sleft(tright)right]$, формулой скорости станет:
[overline{v}=frac{doverline{r}}{dt}=frac{doverline{r}}{ds}frac{ds}{dt}left(6right).]
Величина $Delta s$ – это расстояние между двумя точками по траектории движения тела. Модуль $left|Delta overline{r}right|$ – расстояние между этими точками по кратчайшему направлению – прямой. При сближении рассматриваемых двух точек разница между $Delta s$ и $left|Delta overline{r}right|$ уменьшается. Имеем:
[frac{doverline{r}}{ds}={mathop{lim }_{Delta sto 0} frac{Delta overline{r}}{Delta s} }={mathop{lim }_{Delta sto 0} frac{Delta overline{r}}{left|Delta overline{r}right|} }cdot frac{left|Delta overline{r}right|}{Delta s}=overline{tau }left(7right),]
где $overline{tau }$ – единичный вектор, касательный к траектории движения материальной точки. Кроме этого:
[frac{ds}{dt}=v(8)]
модуль скорости движения точки по траектории. Уравнение (6) представим как:
[overline{v}=frac{doverline{r}}{dt}=frac{ds}{dt}overline{tau }=voverline{tau }left(9right).]
Формула (9) показывает, что мгновенная скорость направлена по касательной к траектории движения тела (материальной точки).
Формулы средней скорости
Вектор средней скорости ($leftlangle overline{v}rightrangle $) при движении между двумя точками определяют как:
[leftlangle overline{v}rightrangle left(t,t+Delta tright)=frac{Delta overline{r}}{left|Delta overline{r}right|}frac{left|Delta overline{r}right|}{Delta t}=frac{Delta overline{r}}{Delta t}left(10right),]
где в скобках у вектора средней скорости указан промежуток времени, для которого найдена средняя скорость; $Delta overline{r}$ – вектор перемещения точки; $Delta t$- время движения.
При неравномерном движении средняя скорость для разных промежутков времени не одинакова. Устремляя $Delta t$ к нулю, мы получим, что средняя скорость стремится к величине мгновенной скорости.
Иногда при вычислении средней скорости (ее называют средне путевой) применяют другую формулу:
[leftlangle vrightrangle =frac{s}{t}left(11right),]
где $s$- весь путь пройденный точкой; $t$ – все время ее движения. В этом случае средняя скорость – это скаляр.
Формулы линейной скорости при движении разных видов
Если тело движется равномерно, скорость постоянная величина. Ее формулой считают:
[v=frac{s}{t}left(12right),]
где $s$ – путь; $t$ – время движения. При равномерном прямолинейном движении у скорости постоянным является не только величина, но и направление, при этом записывают:
[overline{v}=const.]
Если известно ускорение материальной точки как функции от времени ($overline{a}(t)$) и начальная скорость движения тела (${overline{v}}_0(t=0)$), скорость находят, используя формулу:
[overline{v}={overline{v}}_0+intlimits^{t’}_0{overline{a}(t)}dt left(13right).]
Если тело перемещается с постоянным ускорением (при $overline{a}=const$) скорость равна:
[overline{v}={overline{v}}_0+overline{a}t left(14right).]
Угловая и линейная скорости
При движении по кривой вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($omega $), которая характеризует быстроту изменения угла поворота $varphi $:
[omega =frac{dvarphi }{dt}left(15right).]
Связь между линейной и угловой скоростями определена формулой:
[v=Romega left(16right),]
где $R$ – радиус кривизны траектории, по которой движется точка.
Примеры задач с решением
Пример 1
Задание. Положение материальной точки, задано радиус-вектором $overline{r }left(tright),$ который является функцией времени: $overline{r }left(tright)={2t}^4overline{i}+t^2overline{j},$ где $overline{i}$ и $overline{j}$ – единичные векторы осей X и Y (рис.1). Чему равен модуль скорости точки в момент времени $t=1$c?
Решение. В качестве основы для решения задачи воспользуемся формулой скорости:
[overline{v}={frac{doverline{r}}{dt} left(1.1right). }]
Подставим в выражение (1.1) $overline{r }left(tright)=t^4overline{i}+3t^2overline{j},$ получим:
[overline{v}=frac{d}{dt}left({2t}^4overline{i}+t^2overline{j}right)=8t^3overline{i}+2toverline{j} left(1.2right).]
Из уравнения (1.2) имеем:
[left{ begin{array}{c}
v_x=8t^3 \
v_y=2t end{array}
right.left(1.3right).]
Используя теорему Пифагора, величину скорости вычислим как:
[v=sqrt{v^2_x+v^2_y}=sqrt{{left(8t^3right)}^2+{left(2tright)}^2}=sqrt{64t^6+{4t}^2}=sqrt{68}(frac{м}{с}).]
Ответ. $v=sqrt{68}frac{м}{с}$
Пример 2
Задание. С какой скоростью должен лететь самолет с востока на запад на широте $varphi $, чтобы за окном иллюминатора всегда было светло? Радиус Земли считать равным R.
Решение. Сделаем рисунок.
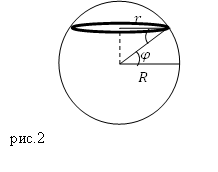
Самолет летит по окружности (рис.2), радиус которой найдем как:
[r=R{cos varphi }left(2.1right).]
Для того чтобы не наступала ночь, тело должно двигаться с угловой скоростью, которая равна скорости вращения Земли вокруг своей оси ($omega $). Для вычисления скорости движения самолета воспользуемся формулой:
[v=omega r=omega R{cos varphi left(2.2right). }]
Угловую скорость вращения Земли найдем, зная, что период вращения Земли составляет 24 ч ($T=24 ч$), следовательно, величину угловой скорости вращения Земли можно считать известной и равной:
[omega =frac{2pi }{T}left(2.3right).]
Окончательно получим, скорость движения самолёта равна:
[v=frac{2pi }{T}R{cos varphi . }]
Ответ. $v=frac{2pi }{T}R{cos varphi }$
Читать дальше: формула модуля равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

