Как найти скорость лодки перпендикулярно течению

Условие задачи:

Определить скорость относительно берега реки лодки, идущей перпендикулярно к течению. Скорость течения реки 1 м/с, скорость лодки относительно воды 2 м/с.

Задача №1.7.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(upsilon_0=1) м/с, (upsilon_1=2) м/с, (upsilon-?)

Решение задачи:

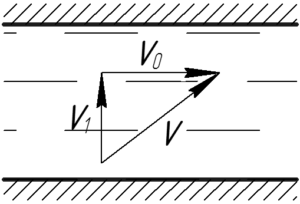Перед нами классическая задача на относительность движения, а точнее на применение правила сложения скоростей. Оно гласит, что скорость тела (лодки в нашем случае) относительно неподвижной системы отсчета (берега) (upsilon) есть векторная сумма скорости тела относительно подвижной системы отсчета (реки) (upsilon_1) и скорость самой подвижной системы отсчета (скорость течения реки) (upsilon_0).

[overrightarrow upsilon = overrightarrow {{upsilon _1}} + overrightarrow {{upsilon _0}} ]

По рисунку к задаче видно, что скорости (upsilon_0) и (upsilon_1) перпендикулярны друг к другу, поэтому искомую скорость (upsilon) можно найти из теоремы Пифагора.

[upsilon = sqrt {upsilon _1^2 + upsilon _0^2} ]

Сосчитаем ответ, подставив в формулу численные значения.

[upsilon = sqrt {{2^2} + {1^2}} = 2,24; м/с = 8,05; км/ч]

Ответ: 8,05 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.6.22 Тело брошено под углом 60 к горизонту с начальной скоростью
1.7.2 Скорость течения реки 1,5 м/с. Какую скорость относительно воды должен иметь
1.7.3 Движение двух автомобилей по шоссе задано уравнениями x1=2t+0,2t^2 и x2=80-4t

Источник

Содержание

Определить скорость относительно берега реки лодки, идущей перпендикулярно
Условие задачи:
Решение задачи:
Ответ: 8,05 км/ч.
Как найти собственную скорость лодки
Сложение скоростей
Как найти скорость лодки перпендикулярно течению
Как найти собственную скорость лодки

Определить скорость относительно берега реки лодки, идущей перпендикулярно

Условие задачи:

Задача №1.7.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

(upsilon_0=1) м/с, (upsilon_1=2) м/с, (upsilon-?)

Решение задачи:

[overrightarrow upsilon = overrightarrow <<upsilon _1>> + overrightarrow <<upsilon _0>> ]

Сосчитаем ответ, подставив в формулу численные значения.

[upsilon = sqrt <<2^2>+ <1^2>> = 2,24; м/с = 8,05; км/ч]

Ответ: 8,05 км/ч.

Источник

Как найти собственную скорость лодки

Как найти собственную скорость лодки
Как решить задачу на скорость реки
Как решать задачи на движение

Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:

Vпр. теч=Vпо теч. — 2Vтеч.

Vпо теч.=Vпр. теч+2Vтеч.

Vтеч.=(Vпо теч. — Vпр. теч)/2

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:

Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Расстояние 24 24

время 24/ (Х-3) 24/ (Х+3)

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

24/ (Х-3) – 24/ (Х+3) = 1/3

Х=21(км/ч) – собственная скорость парохода.

Источник

Сложение скоростей

Пусть человек идёт поперёк плота, плывущего по реке. При этом скорость человека относительно плота перпендикулярна скорости течения (рис. 9.1, вид сверху).

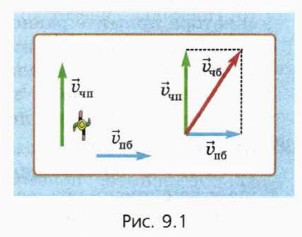
Из правила сложения скоростей (см. § 3) следует:

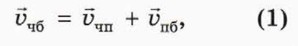
где _чб — скорость человека относительно берега, чп — скорость человека относительно плота, _пб — скорость плота относительно берега (скорость течения).

На рисунке 9.1 справа показано, как графически найти скорость человека относительно берега (красная стрелка). Мы видим, что человек движется не перпендикулярно берегу, поскольку его (вместе с плотом) сносит течением.

Во время переправы через реку лодку тоже сносит течением. Если скорость _лв лодки относительно воды направлена перпендикулярно течению, то её скорость _лб относительно берега (красная стрелка) будет направлена не перпендикулярно берегу, а под некоторым углом α к этому перпендикуляру (рис. 9.2).

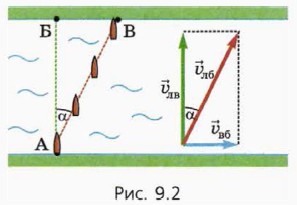
Поэтому лодка попадёт не в точку Б, находящуюся точно напротив начальной точки А, а в точку В, которая расположена ниже точки Б по течению.

На рисунке 9.2 для наглядности изображены некоторые промежуточные положения лодки, чтобы было видно, что она всё время держит курс перпендикулярно берегу, но течение сносит её во время переправы.

1. Моторная лодка переправляется через реку шириной 60 м. Скорость лодки относительно воды направлена перпендикулярно берегу и равна 2 м/с, а скорость течения равна 1 м/с.

а) Сколько времени займёт переправа?

б) Насколько снесёт лодку по течению за время переправы?

в) Какой угол составляет скорость лодки относительно берега с перпендикуляром к берегу?

Обратите внимание: если скорость лодки относительно воды перпендикулярна берегу, течение не влияет на время переправы.

Источник

2020-03-12
Лодка пересекает реку с постоянной относительно воды скоростью $v$, перпендикулярной к течению. Скорость течения реки, ширина которой $d$, равна нулю у берегов и линейно возрастает по мере приближения к середине реки, где она достигает значения $u$. Найти траекторию лодки, а также снос лодки $x_<0>$ вниз по течению, от пункта ее отправления до места причала на противоположном берегу реки.

Написанные уравнения находим для первой параболы из условий:

при $t = 0$ $x = 0$ и $y = 0$, (1)

$v_ = v = const$ или $y = vt$, (2)
$v_ = frac

= ky = frac<2u>y$, (3)

Интегрирование уравнения (3) при учете (1) и (2) дает $x = fract^<2>$. Исключая время $t$, находим уравнение ветви первой параболы. Подставляя в него $y = frac<2>$, находим снос лодки на первой половине ее пути. Уравнение ветви второй параболы легко получить следующим образом. Выберем новое начало координат $X^< prime>O^< prime>Y^< prime>$ в той точке $O^< prime>$ на середине реки, которой достигнет лодка, пройдя первую половину пути. Теперь начальные условия движения запишутся так: при $t = 0$ $x^ < prime>= 0$ и $y^ < prime>= 0$. Далее, $y^ < prime>= vt$, но $v_ = u — frac<2u> y^< prime>$. Решая эти уравнения, как и в первом случае, находим $y^ < prime>= frac <2>— sqrt < frac> <4>— fracd > >$. Возвращаясь к прежним координатам, при помощи соотношений $y = y^ < prime>+ frac<2>$ и $x = x^ < prime>+ frac<2v>$, находим уравнение ветви второй параболы в прежних координатах. Очевидно, что эта ветвь второй параболы будет перевернутым повторением ветви первой параболы.

Траектория состоит из ветвей двух парабол (рис.):

Источник

Как найти собственную скорость лодки

Как найти собственную скорость лодки

Как решить задачу на скорость реки

Как решать задачи на движение

Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:

Vпр. теч=Vпо теч. — 2Vтеч.

Vпо теч.=Vпр. теч+2Vтеч.

Vтеч.=(Vпо теч. — Vпр. теч)/2

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:

Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Расстояние 24 24

время 24/ (Х-3) 24/ (Х+3)

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

24/ (Х-3) – 24/ (Х+3) = 1/3

Х=21(км/ч) – собственная скорость парохода.

Источник

Источник

2.2.1 Как перевести из км/ч в м/с и т. д?

В задачах часто необходимо переводить из одних единиц измерения в другие:

1 км/ч = (1000 м)/(3600 с) = 5/18 м/с,

1 м/с = 18/5 км/ч,

1 км/с = 1000 м/с,

1 см/с = 0,01 м/с,

1 м/мин = 1/60 м/с.

Например, если то для того, чтобы перевести в м/с, нужно умножить на 5/18:

2.2.2 Как найти скорость тела, если известен закон движения?

Закон равномерного движения имеет вид:

Видим, что в этой формуле скорость стоит коэффициентом перед временем. Поэтому, если в условии задачи дан закон движения, необходимо посмотреть на коэффициент перед t — это и есть скорость.

Например, пусть закон движения имеет вид: В данном случае коэффициент перед t равен 5, следовательно,

2.2.3 Как определить скорость по графику координаты от времени?

Закон равномерного движения имеет вид:

Графиком этого закона является прямая линия. Так как nu_x — коэффициент перед t, то nu_x является угловым коэффициентом прямой.

Для графика 1:

То, что график 1 «поднимается вверх», означает — тело едет в положительном направлении оси Ox.

Для графика 2:

То, что график 2 «опускается вниз», означает — тело едет в отрицательном направлении оси Ox.

Для определения Delta x и Delta t выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.

2.2.4 Как найти закон движения, если известны координаты тела в моменты времени и ?

Пусть в момент времени t_1 тело находилось в точке с координатой x_1, а в момент времени t_2 тело находилось в точке с координатой x_2.

Для времени t_1 имеем:

Для времени t_2 имеем:

Решая систему уравнений (2.19) и (2.20), получим

2.2.5 Как найти графически момент и координату встречи двух тел?

Пусть даны законы движения двух тел: и Согласно пункту 2.5 графиками обоих законов являются прямые линии. Необходимо на одном графике построить оба закона.

Графики пересекаются в одной точке. Координаты этой точки и являются временем и местом встречи.

2.2.6 Как аналитически найти координату и время встречи двух тел?

Пусть даны законы движения двух тел: и В момент встречи тела оказываются в одной координате, то есть и необходимо решить уравнение:

Решение уравнения имеет вид:

Для нахождения координаты достаточно подставить вместо t найденное значение в любой из законов движения:

или

2.2.7 Как найти среднюю скорость, если тело половину пути проехало со скоростью а вторую половину пути

По определению (2.8):

В нашем случае, так как на каждой половине пути тело едет с постоянной скоростью, то

Получаем

В общем случае, если весь путь разбить на n равных участков, на каждом из которых тело едет с постоянной скоростью, то

Формула справедлива только если весь путь разбит на равные участки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.8 Как найти среднюю скорость, если тело половину времени проехало со скоростью а вторую половину времени

По определению (2.8):

В нашем случае, так как каждую половину времени тело едет с постоянной скоростью, то

Получаем

В общем случае, если все время разбито на n равных промежутков, на каждом из которых тело едет с постоянной скоростью, то

Формула справедлива только если все время разбито на равные промежутки. Если же разбиение будет иное, то, естественно, формула для нахождения средней скорости, будет иной.

2.2.9 Как найти скорость, с которой движется моторная лодка по течению реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли), равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета nu_0 (в нашем случае — собственная скорость лодки).

При движении по течению вектора и vecu направлены в одну сторону, следовательно, получаем сложение двух векторов, направленных в одну сторону — используем формулу (1.15):

Таким образом, при движении любого тела по течению его скорость определяется формулой

2.2.10 Как найти скорость, с которой движется моторная лодка против течения реки?

Согласно формуле скорость тела относительно неподвижной системы отсчета (в нашем случае земли) равна векторной сумме скорости подвижной системы отсчета u (в нашем случае — скорость реки) и скорости в подвижной системе отсчета nu_0 (в нашем случае — собственная скорость лодки).

Перепишем формулу в виде:

Вектора и направлены в одну сторону, следовательно, получаем вычитание двух векторов, направленных в одну сторону — используем формулу :

2.2.11 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена перпендикулярно течению реки?

В данном случае вектора и vecnu направлены перпендикулярно, следовательно, получаем задачу о сложении взаимно перпендикулярных векторов — используем формулу :

2.2.12 Как найти расстояние, на которое снесет лодку, если ее скорость направлена перпендикулярно скорости реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна vecnu и направлена по прямой OD. В результате, когда тело окажется на противоположном берегу, оно попадет в точке D, и его снесет на длину CD=S.

Треугольник OAB подобен треугольнику OCD:

2.2.13 Как найти скорость, с которой движется моторная лодка, если ее скорость направлена под углом φ к скорости течения реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна vecnu и направлена по прямой OB. Как видим, получили треугольник, в котором известен один из углов — Тогда по теореме косинусов:

2.2.14 Как найти расстояние, на которое снесет лодку, если ее скорость направлена под углом к скорости течения реки?

В результате сложения скоростей по формуле скорость тела относительно земли равна vecnu и направлена по прямой OB. В результате, когда тело окажется на противоположном берегу, оно попадет в точке В, и его снесет на длину АВ=S.

В задачах, когда движение происходит в плоскости, то есть и вдоль оси Ox, и вдоль оси Oy, необходимо введение системы координат для того, чтобы упростить рассмотрение задачи.

Проекция nu_x:

Проекция nu_y:

Формулы и не просто результат математической операции нахождения проекции, nu_x и nu_y имеют физический смысл: со скоростью nu_x тело плывет вдоль оси Ox, то есть по течению; со скоростью nu_y тело переплывает реку. Например, время, за которое тело переплывет реку, можно найти просто поделив ширину реки на nu_y:

Тогда

2.2.15 Под каким углом α нужно направить собственную скорость лодки, чтобы за минимальное время переплыть реку?

Согласно формуле скорость, с которой лодка переплывает реку, равна:

Очевидно, что время будет минимальным, если nu_y будет максимальным, то есть

2.2.16 С какой скоростью машина обгоняет вторую машину, если они движутся в одну сторону?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина также движется вправо со скоростью Скорость обгона — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой :

Так как и направлены в одну сторону, то получили задачу о вычитании векторов, направленных в одну сторону — формула :

Заметим, что при обгоне, естественно поэтому

2.2.17 За какое время проедут мимо друг друга два поезда, двигающиеся в одном направлении?

Пусть длина 1-го поезда L_1, а скорость 2-го поезда L_2. Скорость обгона определяется формулой Тогда

2.2.18 С какой скоростью машина едет навстречу вторую машину, если они движутся в противоположных направлениях?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется влево со скоростью Скорость движения навстречу — это скорость, с которой 1-ая машина движется относительно 2-ой, то есть — это относительная скорость, и она определяется формулой :

Перепишем эту формулу в виде:

2.2.19 За какое время проедут мимо друг друга два поезда, двигающиеся в противоположных направлениях?

Пусть длина 1-го поезда L_1, а скорость 2-го поезда L_2. Скорость обгона определяется формулой Тогда

2.2.20 Как найти относительную скорость, если тела движутся по взаимно перпендикулярным направлениям?

Пусть 1-ая машина движется вправо со скоростью а 2-ая машина движется перпендикулярно первой со скоростью Относительная скорость определяется формулой :

Так как вектора и перпендикулярны, то воспользуемся формулой :

Источник

Продолжаем учиться решать задачи на закон сложения скоростей.

Рассмотрим следующие задачи.

Лодка движется по реке. Опять, в качестве неподвижной системы отсчета – дерево, растущее на Земле, подвижной системы отсчета возьмём течение реки (чтобы это течение визуализировать, представьте опавший лист на поверхности воды).

Тогда,

A) скорость лодки (Тела) Относительно Подвижной системы отсчета (течения реки) (ϑтоп) – скорость лодки относительно листка, т.е. скорость лодки в стоячей воде,

B) скорость лодки относительно Земли (дерева) – скорость лодки (Тела) Относительно неподвижной системы отсчета (Земли) (ϑтоз),

C) скорость течения (листка) – скорость Подвижной системы отсчета (течения реки) Относительно неподвижной (Земли) (ϑпоз).

Задача 1.

Найти скорость лодки относительно берега ϑтоз, если она стартует перпендикулярно берегу, учитывая, что скорость лодки относительно упавшего в воду листа (относительно течения воды) ϑтоп равна 3 м/с, а скорость движения листка относительно берега (скорость течения воды) ϑпоз равна 4 м/с.

Решение.

Запишем «Дано» к этой задаче, сделаем чертёж и запишем закон сложения скоростей в векторном виде. (Наверное, Вы уже успели заметить, что все задачи по этой теме решаются по одному алгоритму).

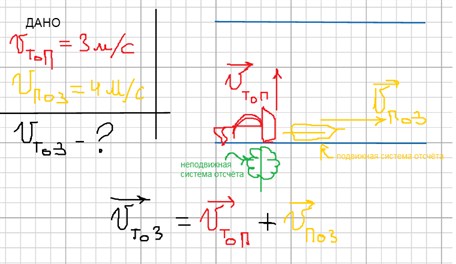
Построим искомый вектор, как сумму векторов.

Видим, что вектор ϑтоз – гипотенуза прямоугольного треугольника с катетами /ϑтоп/ = 3 м/с и /ϑпоз/ = 4 м/с . Решить эту задачу теперь можно и устно.

Ответ: скорость, с какой лодка движется относительно берега ϑтоз = 5 м/с.

Задача 2.

Моторная лодка движется из А в В 80 секунд. Найти скорость и направление движения лодки относительно воды, если скорость течения реки ϑпоз = 3 м/с, а ширина реки 320 м.

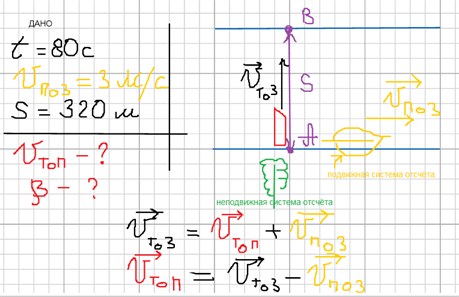ϑтоз = S/t

ϑтоз = 320 м / 80 с = 4 м/с

Построим разность векторов ϑтоз и ϑпоз.Нетрудно посчитать, что ϑтоп = 5 м/с. Теперь осталось вычислить угол α. Так как при помощи построения мы получили прямоугольный треугольник, то sin α = 0,3/0,5 = 0,6, используя таблицу Брадиса, находим α = 36⁰, β= 90⁰ + 36⁰ = 126⁰_.

Ответ: чтобы попасть из А в В моторная лодка должна двигаться относительно воды со скоростью ϑтоп = 5 м/с, под углом 126⁰ к направлению течения.

И ещё одна задачка.

Задача 2.

Лодочник направляет лодку под углом β = 80⁰ к направлению течения. Какой будет скорость движения лодки относительно воды ϑтоп, если скорость течения ϑпоз и относительно берега лодка движется под углом α = 0,5 β?

Решение.

Сделаем чертёж к этой задаче.

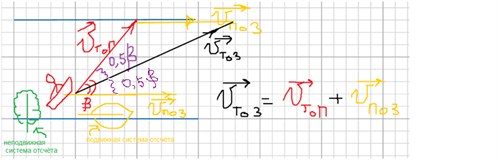0,5 β = 0,5 · 80⁰ = 40⁰

Перечертим чертёж ещё раз, подписав вершины полученного ромба.

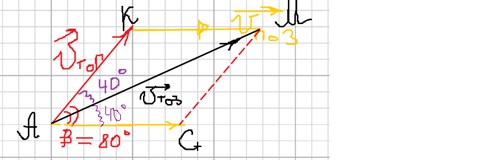Углы КАМ и КМС в ромбе АКМС равны, АМ – гипотенуза, значит, в треугольнике АКМ углы КАМ и АМК тоже равны и, значит, этот треугольник равнобедренный.

Если треугольник АКМ равнобедренный, то катеты АК и КМ равны и следовательно /ϑтоп/ = /ϑпоз/.

Ответ: /ϑтоп / = /ϑпоз/.

Остались вопросы? Не знаете, как решать задачи на звкон сложения скоростей?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Источник

Лодка двигаясь перпендикулярно к берегу, оказалась на другом берегу на расстоянии 25 метров ниже по течению через 1 мин 40 с. Ширина реки 100 м. Определить скорость лодки и скорость течения реки.

Оцените сложность задачи:

0 голосов, средняя сложность: 0.0000

Решения задачи

Данные задачи: лодка переплывает реку

Ширина реки	b	100	м
Смещение лодки	a	25	м
Время в пути	t	100	с
Скорость лодки	υ_л	?
Скорость реки	υ_р	?

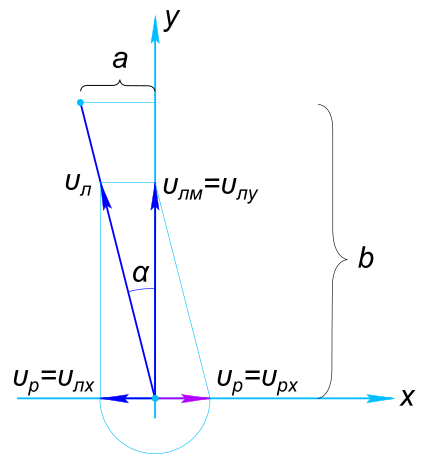
Изобразим на рисунке условие задачи

За время пути перемещение лодки складывается из двух взаимно перпендикулярных перемещений – поперек реки и вдоль реки

$ vect{S_{л}} = vect{S_{x}}+vect{S_{y}} $

Согласно закону прямолинейного равномерного поступательного движения составляем уравнение

$ frac{b}}{υ_{лм}}= frac{S_{x}}{υ_{р}}=t $

Откуда находим

$ υ_{р} = frac{S_{a}}{t}=frac{25}{100}=0,25 frac{м}{с} $

$ υ_{лм} = frac{b}{t}=frac{100}{100}=1 frac{м}{с} $

Тогда

$ υ_{л} = sqrt{(υ_{лм})^{2}+(υ_{р})^{2}}=sqrt{(1)^{2}+(0,25})^{2}}=1,03 frac{м}{с} $

Ответ:

$ Скорость реки 1 frac{м}{с}, а скорость лодки 1,03 frac{м}{с} $

Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь

Источник

Условие задачи:

Дано:

Решение задачи:

Ответ: 8,05 км/ч.

Смотрите также задачи:

Определить скорость относительно берега реки лодки, идущей перпендикулярно

Условие задачи:

Решение задачи:

Ответ: 8,05 км/ч.

Как найти собственную скорость лодки

Сложение скоростей