Как найти скорость лодки в стоячей воде

Как найти собственную скорость лодки

Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение – самое главное в решении любого типа задач.

Инструкция

В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.

Первое, что необходимо выучить и знать “на зубок” – формулы. Запишите и запомните:

Vпо теч=Vс+Vтеч.

Vпр. теч.=Vс-Vтеч.

Vпр. теч=Vпо теч. – 2Vтеч.

Vпо теч.=Vпр. теч+2Vтеч.

Vтеч.=(Vпо теч. – Vпр. теч)/2

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, найдем:

Vтеч = (21,8 – 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Расстояние 24 24

Скорость Х-3 Х+3

время 24/ (Х-3) 24/ (Х+3)

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

20 мин=1/3 часа.

24/ (Х-3) – 24/ (Х+3) = 1/3

24*3(Х+3) – (24*3(Х-3)) – ((Х-3)(Х+3))=0

72Х+216-72Х+216-Х2+9=0

441-Х2=0

Х2=441

Х=21(км/ч) – собственная скорость парохода.

Ответ: 21 км/ч.

Обратите внимание

Скорость плота считается равной скорости водоема.

Источники:

• решение задач на течение

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Привет! У тех, кто готовится к ОГЭ, возникает много вопросов по поводу задач на движение из второй части. И один из возможных вариантов таких задач – это задача про лодку, которая плывёт по течению и против течения. Сегодня разберем конкретный пример такой задачи:

Моторная лодка прошла 45 км против течения реки и вернулась в пункт отправления. При этом на обратный путь она затратила на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.

• Шаг № 1

Давайте для начала разберемся в самой ситуации. У каждой моторной лодки есть двигатель (мотор), который приводит её в движение. Если лодка плывёт, например, по пруду со стоячей водой, то она двигается только благодаря мотору. Скорость лодки в данном случае называется собственная скорость лодки. Её ничего не подгоняет и ничего не тормозит. Именно скорость лодки в неподвижной (стоячей) воде (то есть её собственную скорость) и просят найти авторы задания. То, что нужно найти, в задачах обозначается за «Х».

Итак, собственная скорость лодки = Х.

Лодка будет плыть с собственной скоростью только в неподвижной воде. Если переместить её на реку, то мы столкнёмся с таким явлением, как течение. В реке вода не стоит на месте: она движется в определённую сторону. Скорость течения реки в нашем задании = 3 км/ч.

Что же произойдёт, если лодка будет плыть по течению? Во-первых, её будет приводить в движение мотор. А во-вторых, ее будет подгонять течение. Логично, что по течению лодка будет двигаться быстрее, чем в стоячей воде.

Но как же найти скорость лодки по течению? Очень просто! Она равна сумме собственной скорости лодки и скорости течения реки.

Так как скорость течения нам известна по условию, а собственную скорость лодки мы уже обозначили за «Х», то нам лишь осталось подставить в формулу наши значения. То есть в нашем случае вычислить скорость лодки по течению можно так:

Vпо течению = Vсобственная + Vтечения

Vпо течению = Х + 3 км/ч.

А если лодка будет плыть против течения? В этом случае течение будет её не подгонять, а тормозить. Ведь вода движется в одну сторону, а лодка – в противоположную.

Значит теперь скорость будет меньше, чем в стоячей воде. Найти её можно так: вычесть из собственной скорости лодки скорость течения реки:

Вычислим скорость против течения для нашего случая:

Vпротив течения = Vсобственная – Vтечения

Vпротив течения = Х – 3 км/ч.

Отлично! Перед тем, как перейти к дальнейшим действиям, вспомним формулы для задач на движение:

• Шаг №2

Теперь давайте оформим таблицу, в которую занесем все наши данные. Так мы точно не запутаемся!

Для начала заполним столбик «Расстояние». Для пути против течения оно равно 45 км. Сказано, что лодка вернулась назад. В этом случае на обратном пути по течению она проплыла ровно столько же!

Со скоростями мы уже разобрались. Скорость по течению = Х + 3 км/ч, а против течения = Х – 3 км/ч.

Теперь разберемся со временем. Напомню, что оно вычисляется по формуле: расстояние поделить на скорость. Расстояния у нас есть, скорости тоже, и записать время нам ничего не мешает!

Отлично, все данные записаны, теперь переходим к основному решению!

• Шаг №3

Обратимся к условию ещё раз. Сказано, что на обратный путь по течению лодка затратила на 2 часа меньше, чем на путь против течения. Так что теперь работаем со временем.

Давайте обозначим время движения против течения за t1, а время движения по течению t2. Если на обратный путь было затрачено на 2 часа меньше, то путь «туда» на 2 часа больше.

Из вышесказанного делаем вывод, что t1 > t2 на 2 часа. Это значит, что если из t1 вычесть t2, то получится 2.

t1 – t2 = 2

А теперь подставим в наше выражение t1 – t2 = 2 вместо t1 и t2 наши значения из таблицы. Тогда мы получим замечательное уравнение, которое и поможет нам прийти к ответу.

• Шаг №4

Мы получили дробно-рациональное уравнение. Это значит, что неизвестный «Х» стоит в знаменателе.

И первый шаг в решении подобных уравнений – это запись ОДЗ (области допустимых значений). ОДЗ показывает, каким числом «Х» может быть, а каким – нет.

«Х» стоит в знаменателе, а основное, что мы знаем про знаменатель – это то, что он не может быть равен нулю, потому что на ноль делить нельзя. Запишем знаменатели наших дробей и отметим, что они не равны нулю:

1) Х – 3 ≠ 0

2) Х + 3 ≠ 0

Продолжаем работать с этой записью, как с уравнением:

1) Х ≠ 3

2) Х ≠ – 3

Значит, ОДЗ: Х ≠ ±3. “Х” также должен быть больше нуля, так как скорость (а за “Х” мы обозначили именно её) не может быть отрицательной.

Итог шага №4: ОДЗ: Х ≠ ±3; Х > 0

• Шаг №5

Продолжаем работу с уравнением. Мы разобрались с ОДЗ, а значит, можем с чистой совестью избавиться от знаменателя. Для этого умножим обе части уравнения на наименьший общий знаменатель.

Наименьший общий знаменатель (НОЗ) – это наименьшее число, которое делится на все знаменатели рассматриваемых дробей. В нашем случае это (Х – 3) (Х + 3). Он делится и на (Х – 3), и на (Х + 3). Вперед!

Чтобы лучше разобраться в сложных числовых махинациях, обратимся к подробной записи:

Обратите внимание, что дроби слева сокращаются, таким образом исчезает знаменатель.

Итак, вот что у нас получается:

45(х + 3) – 45(х – 3) = 2(х – 3)(х + 3)

Обратим внимание на скобки (х – 3)(х + 3). Они представляют собой разложенную разность квадратов. Вспомним эту формулу:

Скобки (х – 3)(х + 3) соответствуют части (a + b)(a – b) в формуле. Чтобы свернуть её обратно, нам нужно записать квадрат первого числа(Х^2), поставить знак минус, а затем записать квадрат второго числа (3^2 = 9).

45(х + 3) – 45(х – 3) = 2(х^2 – 9)

Предлагаю перенести все элементы в одну сторону. Напомню, что при переходе в противоположную сторону элемент должен поменять знак. То есть если справа мы видим 2(х^2 – 9), то перенести влево должны
– 2(х^2 – 9). При этом справа ничего не остаётся, поэтому ставим ноль. Приступим!

45(х + 3) – 45(х – 3) – 2(х^2 – 9) = 0

Теперь давайте раскроем скобки и приведем подобные слагаемые.

45(х + 3) – 45(х – 3) – 2(х^2 – 9) = 0

45х + 135 – 45х + 135 – 2х^2 + 18 = 0

Слагаемые 45х и – 45х в сумме дают ноль, поэтому их можно больше не записывать. Они «взаимоуничтожаются»

288 – 2х^2 = 0

Теперь перенесем все числовые значения вправо, а буквенные оставим слева, а затем продолжим решение:

– 2х^2 = – 288

x^2 = – 288/- 2

х^2 = 144

х = ±√144 = ±12.

Мы получили два корня. Корень – 12 нам не подходит, так как он отрицательный, а выше мы писали, что х > 0. А вот корень 12 удовлетворяет всем условиям, он нам подходит. Так как за “Х” мы обозначили собственную скорость лодки, которую и требуется найти в задании, то, решив это уравнение, мы получили ответ!

Ответ: 12 км/ч.

А вот решение без лишних пояснений:

Надеюсь, все было максимально понятно:)

До новых встреч!!

Как найти собственную скорость лодки

Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение — самое главное в решении любого типа задач.

В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.

Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:

Vпр. теч=Vпо теч. — 2Vтеч.

Vпо теч.=Vпр. теч+2Vтеч.

Vтеч.=(Vпо теч. — Vпр. теч)/2

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:

Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Расстояние 24 24

время24/ (Х-3) 24/ (Х+3)

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

24/ (Х-3) – 24/ (Х+3) = 1/3

Х=21(км/ч) – собственная скорость парохода.

Источник

Как найти собственную скорость

Согласно учебной программе по математикедети должны научиться решать задачи на движение еще в начальной школе. Однако задачи такого вида часто вызывают уучащихся затруднение. Важно,чтоб ребенок понял, что такое собственная скорость, скорость течения, скорость по течению и скорость против течения. Только при этом условии школьник сможет легко решать задачина движение.Вам понадобится

Собственная — это скорость катера или другого средства передвижения в неподвижной воде. Обозначьте ее — V собств.
Вода в реке находится в движении. Значит она имеет свою скорость, которая называется скоростью течения (V теч.)
Скорость катера по течению реки обозначьте — V по теч., а скорость против течения — V пр. теч.

Теперь запомните формулы, необходимые для решения задач на движение:
V пр. теч.= V собств. — V теч.
V по теч.= V собств. + V теч.

Итак, исходя из этих формул, можно сделать следующие выводы.
Если катер движется против течения реки, то V собств. = V пр. теч. + V теч.
Если катер движется по течению, то V собств. = V по теч. — V теч.

Решим несколько задач на движение по реке.
Задача 1. Скорость катера против течения реки 12,1 км/ч. Найдите собственную скорость катера, зная , что скорость течения реки 2 км/ч.
Решение: 12,1 + 2 = 14, 1 (км/ч) — собственная скорость катера.
Задача 2. Скорость катера по течению реки 16,3 км/ч, скорость течения реки 1,9 км/ч. Сколько метров прошел бы это катер за 1 мин., если находился в стоячей воде?
Решение: 16,3 — 1,9 = 14,4 (км/ч) — собственная скорость катера. Переведем км/ч в м/мин: 14,4 / 0,06 = 240 (м/мин.). Значит, за 1 минуту катер прошел бы 240 м.
Задача 3. Два катера отправились одновременно навстречу друг другу из двух пунктов. Первый катер двигался по течению реки, а второй — против течения. Встретились они через три часа. За это время первый катер прошел 42 км, а второй — 39 км.Найдите собственную скорость каждого катера, если известно, что скорость течения реки 2 км/ч.
Решение: 1) 42 / 3 = 14 (км/ч) — скорость движения по течению реки первого катера.
2) 39 / 3 = 13 (км/ч) — скорость движения против течения реки второго катера.
3) 14 — 2 = 12 (км/ч) — собственная скорость первого катера.
4) 13 + 2 = 15 (км/ч) — собственная скорость второго катера.

Источник

Как найти собственную скорость лодки

• Как найти собственную скорость лодки
• Как решить задачу на скорость реки
• Как решать задачи на движение

Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:

Vпр. теч=Vпо теч. — 2Vтеч.

Vпо теч.=Vпр. теч+2Vтеч.

Vтеч.=(Vпо теч. — Vпр. теч)/2

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:

Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Расстояние 24 24

время 24/ (Х-3) 24/ (Х+3)

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

24/ (Х-3) – 24/ (Х+3) = 1/3

Х=21(км/ч) – собственная скорость парохода.

Источник

Как найти скорость в стоячей воде

• Как найти собственную скорость лодки
• Как найти скорость, время, расстояние
• Как решать задачи на движение

Первое, что необходимо выучить и знать «на зубок» – формулы. Запишите и запомните:

Vпр. теч=Vпо теч. – 2Vтеч.

Vпо теч.=Vпр. теч+2Vтеч.

Vтеч.=(Vпо теч. – Vпр. теч)/2

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, найдем:

Vтеч = (21,8 – 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Расстояние 24 24

время 24/ (Х-3) 24/ (Х+3)

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

24/ (Х-3) – 24/ (Х+3) = 1/3

Х=21(км/ч) – собственная скорость парохода.

Ответ или решение 1

Скорость лодки плывущей по течению реки, будет больше скорости лодки плывущей в стоячей воде, на скорость этого самого течения. Потому что, течение помогает лодке плыть. Следовательно чтобы узнать скорость лодки в стоячей воде, необходимо от скорости лодки плывущей по течению вычесть скорость течения реки. Узнаем собственную скорость лодки, если, нам известно что ее скорость по течению 19,2 км в час, а скорость течения 2,6 км в час.

19,2 – 2,6 = 16,6 км в час.

Ответ: Скорость лодки в стоячей воде составляет 16,6 км в час.

Разделы: Математика

Данный материал представляет собой систему задач по теме “Движение”.

Цель: помочь учащимся более полно овладеть технологиями решения задач по данной теме.

Задачи на движение по воде.

Очень часто человеку приходится совершать движения по воде: реке, озеру, морю.

Сначала он это делал сам, потом появились плоты, лодки, парусные корабли. С развитием техники пароходы, теплоходы, атомоходы пришли на помощь человеку. И всегда его интересовали длина пути и время, затраченное на его преодоление.

Представим себе, что на улице весна. Солнце растопило снег. Появились лужицы и побежали ручьи. Сделаем два бумажных кораблика и пустим один из них в лужу, а второй – в ручей. Что же произойдет с каждым из корабликов?

В луже кораблик будет стоять на месте, а в ручейке – поплывет, так как вода в нем «бежит» к более низкому месту и несет его с собой. То же самое будет происходить с плотом или лодкой.

В озере они будут стоять на месте, а в реке – плыть.

Рассмотрим первый вариант: лужа и озеро. Вода в них не движется и называется стоячей.

Кораблик поплывет по луже только в том случае, если мы его подтолкнем или если подует ветер. А лодка начнет двигаться в озере при помощи весел или если она оснащена мотором, то есть за счет своей скорости. Такое движение называют движением в стоячей воде.

Отличается ли оно от движения по дороге? Ответ: нет. А это значит, что мы с вами знаем как действовать в этом случае.

Задача 1. Скорость катера по озеру равна 16 км/ч.

Какой путь пройдет катер за 3 часа?

Следует запомнить, что скорость катера в стоячей воде называют собственной скоростью.

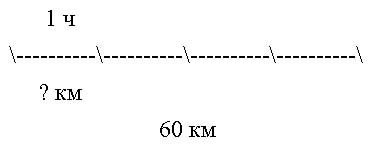
Задача 2. Моторная лодка за 4 часа проплыла по озеру 60 км.

Найдите собственную скорость моторной лодки.

Задача 3. Сколько времени потребуется лодке, собственная скорость которой

равна 28 км/ч, чтобы проплыть по озеру 84 км?

Итак, чтобы найти длину пройденного пути, необходимо скорость умножить на время.

Чтобы найти скорость, необходимо длину пути разделить на время.

Чтобы найти время, необходимо длину пути разделить на скорость.

Чем же отличается движение по озеру от движения по реке?

Вспомним бумажный кораблик в ручье. Он плыл, потому что вода в нем движется.

Такое движение называют движением по течению. А в обратную сторону – движением против течения.

Итак, вода в реке движется, а значит имеет свою скорость. И называют ее скоростью течения реки. ( Как ее измерить?)

Задача 4. Скорость течения реки равна 2 км/ч. На сколько километров река относит

любой предмет (щепку, плот, лодку) за 1час, за 4 часа?

Ответ: 2 км/ч, 8 км/ч.

Каждый из вас плавал в реке и помнит, что по течению плыть гораздо легче, чем против течения. Почему? Потому, что в одну сторону река «помогает» плыть, а в другую – «мешает».

Те же, кто не умеет плавать, могут представить себе ситуацию, когда дует сильный ветер. Рассмотрим два случая:

1) ветер дует в спину,

2) ветер дует в лицо.

И в том и в другом случае идти сложно. Ветер в спину заставляет бежать, а значит, скорость нашего движения увеличивается. Ветер в лицо сбивает нас, притормаживает. Скорость при этом уменьшается.

Остановимся на движении по течению реки. Мы уже говорили о бумажном кораблике в весеннем ручье. Вода понесет его вместе с собой. И лодка, спущенная на воду, поплывет со скоростью течения. Но если у нее есть собственная скорость, то она поплывет еще быстрее.

Следовательно, чтобы найти скорость движения по течению реки, необходимо сложить собственную скорость лодки и скорость течения.

Задача 5. Собственная скорость катера равна 21 км/ч, а скорость течения реки 4 км/ч. Найдите скорость катера по течению реки.

Теперь представим себе, что лодка должна плыть против течения реки. Без мотора или хотя бы весел, течение отнесет ее в обратную сторону. Но, если придать лодке собственную скорость ( завести мотор или посадить гребца), течение будет продолжать отталкивать ее назад и мешать двигаться вперед со своей скоростью.

Поэтому, чтобы найти скорость лодки против течения, необходимо из собственной скорости вычесть скорость течения.

Задача 6. Скорость течения реки равна 3 км/ч, а собственная скорость катера 17 км/ч.

Найдите скорость катера против течения.

Задача 7. Собственная скорость теплохода равна 47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость теплохода по течению и против течения.

Ответ: 51,9 км/ч; 42,5 км/ч.

Задача 8. Скорость моторной лодки по течению равна12,4 км/ч. Найдите собственную скорость лодки, если скорость течения реки 2,8 км/ч.

Задача 9. Скорость катера против течения равна 10,6 км/ч. Найдите собственную скорость катера и скорость по течению, если скорость течения реки 2,7 км/ч.

Ответ: 13,3 км/ч; 16 км/ч.

Связь между скоростью по течению и скоростью против течения.

Введем следующие обозначения:

V_с. – собственная скорость,

V_теч. – скорость течения,

V _{по теч.} – скорость по течению,

V _пр.теч. – скорость против течения.

Тогда можно записать следующие формулы:

Попытаемся изобразить это графически:

Вывод: разность скоростей по течению и против течения равна удвоенной скорости течения.

Vno теч — Vnp. теч = 2 Vтеч.

Vтеч = (V по теч – Vnp. теч ): 2

1) Скорость катера против течения равна 23 км/ч, а скорость течения 4 км/ч.

Найдите скорость катера по течению.

2) Скорость моторной лодки по течению реки равна 14 км/ч/ а скорость течения 3 км/ч. Найдите скорость лодки против течения

Задача 10. Определите скорости и заполните таблицу:

Источник

Как найти собственую скорость лодки

0

Пн-Пт 9:00-19:00
Сб-Вс 10:00-16:00

• Море моторов
• Как рассчитать по формулам скорость лодки?

Как рассчитать по формулам скорость лодки?

Собрали для Вас актуальные формулы, которые могут оказаться полезными каждому

8 июля 2020 1 188

✓ Формула 1

На примере разберем, как находить скорость лодки.

Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:

Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

✓ Формула 2

Самым простым методом самостоятельного расчета предельной скорости лодки считается использование формулы, учитывающей параметры двигателя.

Для этого используется формула вычисления двигателя V = NK/R, где искомый параметр V – скорость километров в час, R – сопротивление движению (его вы можете взять в технической документации своего катера), K – коэффициент полезной деятельности винта. Определяется он в зависимости от типа лодки. Так, для спортивного катера его значение — 160, для крупных винтов — 140, для средних и малых — 120 и 100 соответственно.

Параметр N – мощность работы двигателя катера. Эту информацию вы можете рассчитать самостоятельно или обратиться за помощью к технической документации. Для того, чтобы вычислить предел скорости катера, возьмите максимально допустимую мощность. Этот метод позволяет рассчитать предел максимальной скорости катера достаточно точно, однако не следует забывать про вероятную погрешность.

Возможно вам будет интересным

История производства подвесных лодочных моторов

С чего все началось? Рассказываем!

15 сентября 2020 403

Что такое виндсерфинг и зачем он нужен?

Подробнее рассказываем в нашей статье!

31 августа 2020 323

Этапы получения прав на маломерное судно

Получение любых прав на средства передвижения требуют определенных затрат, например: сбор необходимых документов, обучение, экзамены и многое другое. Рассказываем подробнее.

27 августа 2020 410

В чем плюсы бронирования лодок ПВХ?

Рассказываем особенности, читайте

20 августа 2020 364

5 мифов про лодки ПВХ

Таинственные лодки ПВХ и какие мифы их окружают?

17 августа 2020 331

Почему покупают детские велосипеды?

Хотите порадовать ребенка велосипедом? Отлично, наш ассортимент полон детских велосипедов!

10 августа 2020 319

Что нужно знать перед покупкой велосипеда?

Какие бывают велосипеды? Как выбрать? Читайте в статье

27 июля 2020 364

Как выбрать лодочный мотор?

Отвечаем на Вопросы наших покупателей

21 июля 2020 332

Что такое килеватость судна и на что влияет?

Читайте подробнее в статье!

14 июля 2020 920

Пункт выдачи заказов:
г. Санкт-Петербург, ул. Софийская д. 8к1 БЦ Крол

Пн-Сб 10:00-19:00
Вс 10:00-18:00

Остались вопросы?

Задайте их нам прямо сейчас!

© Море Моторов, 2021 | Все права защищены

Предложения, размещенные на сайте more-motorov.ru, не являются публичной офертой

Пожалуйста, введите Ваши данные, и менеджер свяжется с Вами в ближайшее время

Источник

Задачи на движение по реке

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.

Через уравнение.

S – пройденный путь, растояние, которое прошла, например, лодка. (км)

t – время, за которое она прошла расстояние S. (часов, минут)

V – собственная её скорость (км/ч, м/ч)

Такие задачи решаются далее: если известны: (под формулы подставляем числа)

t и V, то перемножаем – t * V, получаем S.

t и S, то расстояние делим время – S : t, получаем V

S и V, также – S : V, получаем t

Также если в задаче указана V (её ищем)

по течению, то V собственная + V по течению

против течения, то V собств. – V прот. теч.

Тогда формулы звучат так: если известны:

t и V, то t * (V с. +/- V) = S

t и S, то S : t = V с. +/- V

V и S, то S : (V c. +/- V) = t

Теперь ещё раз:

V c. – собственная скорость

V c. + V – скорость + скорость по теч.

V c. – V – скорость + скорость прот. теч.

Ну так чтоли… Плохой из меня учитель(((