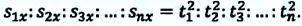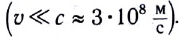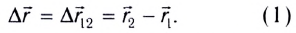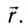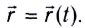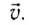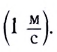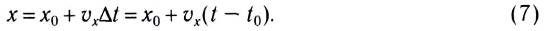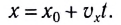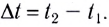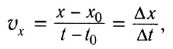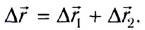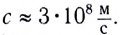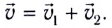Для описания движения используют три величины — скорость, время и расстояние. В координатном углу на горизонтальном луче отмечается время, на вертикальном — пройденное расстояние. Скорость объекта при равномерном движении можно вычислить.
Чтобы по графику движения определить скорость объекта (v), нужно узнать, какое расстояние (s) проходит объект за некоторое время (t), и найти частное расстояния и времени:
v=s:t
.
Для расчёта скорости можно взять любой удобный временной отрезок и пройденное за это время расстояние.
Пример:
по данному графику найти скорость движения объекта.
Решение.
(1) способ. За (1) час пройдено (8) км, то есть скорость объекта равна (8) км/ч.
(2) способ. За (5) часов пройдено (40) км, поэтому скорость объекта равна (40:5=8) км/ч.
Ответ: (8) км/ч.
При равномерном движении график представляет собой отрезок. И наоборот, в каждой точке отрезка скорость одинаковая.
Обрати внимание!
Чем больше скорость движения объекта, тем график круче.
Остановка в пути обозначается на графике движения горизонтальными отрезками, так как пройденное расстояние не меняется.
По данному графику движения можно определить, что с (9):(00) до (11):(00) была остановка в пути.
Источники:
Изображения: график движения. © ЯКласс.
Поскольку при
движении материальной точки изменяется
ее положение относительно выбранной
системы отсчета, то возникает важный
вопрос: Как быстро это положение
изменяется? Физической величиной, с
помощью которой отвечают на этот вопрос,
является скорость.
Скоростью
материальной
точки
называется
вектор, равный производной радиус-вектора
по времени:
(1.5)
или в проекциях
на декартовы координатные оси
,
,
,
(1.6)
.
Так как хорда
(рис 1.2), стягивающая дугу траектории
l12,
в пределе при
совпадает с касательной, то вектор
скорости направлен по касательной к
траектории в сторону движения материальной
точки.
В частности, если
модуль скорости
,
то такое движение называется равномерным.
Если детальная
характеристика движения за промежуток
времени
несущественна, то используют средние
величины:
– средний вектор
скорости
,
(1.7)
– модуль скорости
, (1.8)
– средняя
скорость
,
(1.9)
где S
– путь, пройденный материальной точкой
за время t.
Обратите внимание на то, что
–
скалярная величина. В общем случае
произвольного движения материальной
точки
.
Часто полезно
бывает знать, с какой скоростью изменяется
со временем
расстояние между
материальной точкой и началом координат
(как быстро изменяется модуль радиус-вектора
),
и с какой скоростью изменяется направление
радиус-вектора относительно осей
координат системы отсчета? Ответить на
эти вопросы проще всего, если воспользоваться
естественной формой представления
радиус-вектора
,
(1.10)
которая учитывает
тот факт, что у любого вектора есть две
естественные характеристики: величина
и направление.
Здесь
– орт вектора
,
то есть вектор, модуль которого равен
единице
,
а направление совпадает с направлением
радиус-вектора
.
Используя (1.5) и
(1.10), получим
.
(1.11)
В соотношении
(1.11) вектор
представлен в виде двух составляющих,
первая из которых
(1.12)
характеризует
скорость изменения модуля радиус-вектора
и направлена вдоль
|
|
.
(1.13)
характеризует в сторону его поворота. Действительно,
то |
(угол поворота
радиус-вектора
за время
).
При этом
,
значит при
.
Поэтому
.
Здесь надо учесть, что
.
Таким образом,
;
.
Выводы:
Скорость материальной точки – есть
производная радиус-вектора по времени,
характеризует быстроту изменения
радиус-вектора как по модулю, так и по
направлению, направлена по касательной
к траектории движения.
Контрольные
вопросы
1.4. Покажите,
что
.
1.5. Может ли при
прямолинейном движении выполняться
условие
.
При каком движении выполняется равенство
между этими величинами?
1.6. Что вы можете
сказать о характере движения и виде
траектории, если: а)
;
б)
;
в)
,
;
г)
,
;
д)
,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Давно планировал начать рубрику для школьников и студентов (а может и не только для них), в которой будет рассказываться о методах решения конкретных задачи и подготовке к экзаменам по физике. Само собой, в этой же рубрике мы поговорим и про егэ по физике, которое пугает ребят больше всего. Пусть рубрика на канале называется #инженер репетитор
Ну а начнем с самого простого – научимся решать задачи на скорость. Эти задачки являются базой для дальнейшего понимания кинематики и динамики, и будут вылезать на протяжении всей механики.
Давайте сначала кратенько вспомним, а что такое скорость?
Кратко про скорость в физике
Скорость в физике – это то насколько быстро изменяется некоторая физическая величина с течением времени. Векторная величина, которая имеет размер и направление.
Например, мы нагреваем комнату. Каждый час система отопления прибавляет в комнате один градус. Значит, скорость прогрева комнаты составляет один градус в час. Или едем мы на велосипеде и за один час проезжаем 20 км. Значит, мы едем со скоростью 20 километров в час.
Вот собственно и всё, что нужно помнить из теории по этому вопросу.
Задачки на скорость обычно сконцентрированы в разделе механики, но вылезают и в других более серьезных разделах физики – скорость света, время течения какой-то реакции, скорость изменения чего-то.
Однако, разобравшись как решать подобные задачи для движения чего-то материального, разобраться и в других разделах проблем не составит. Так или иначе, когда говорят про задачи на скорость, обычно подразумевают именно кинематику и динамику.
Итак, а какие собственно задачи в этой теме бывают и как их решать :)?
Задачи по скорости и их типы
Все задачи из этой темы обычно сводятся к тому, что нужно вытащить скорость из некоторой закономерности. Для этого нужно понимать и примерно помнить формулировки, связанные со скоростью. Их не так много. Не забываем и классические косяки – например привести всё к единой системе СИ.
Самые простые задачки на скорость
Самый простой случай, когда нам известно пройденное расстояние и время, а нужно найти скорость:
S = v * t, значит V = S / t
Находим скорость в м/с или км/ч.
Задачки на “встречу”
Задачки на “встречу”. Кто-то едет навстречу кому-то или кто-то кого-то встретил. Обычно такие задачки, с помощью витиеватого условия, пытаются заморочить читателю голову, но суть-то от этого не меняется.
Нам, например, задают граничные условия и указывают, что два мотоциклиста едут по одной дороге в одну сторону и выехали одновременно. Дальше они встретились. Ну и один другого подождал на точке встречи. Один едет 20 минут, а другой едет со скоростью 50 км/ч 60 минут. Найдите скорость первого мотоциклиста. Проблем быть не должно 🙂
Считаем по приведенной выше формуле сколько проехал второй мотоциклист до времени встречи. Из этого расстояния выражаем скорость первого мотоциклиста. Ведь в точке встречи расстояние, которое они проехали было одинаковым. Вот вам и решение.
Вообще, относительно, всей этой тематики, очень полезно освоить процесс рисования чертежей и схем. Нужно сделать доходчивую и понятную схему, которая будет в нужном масштабе отражать все перемещения и их особенность. Это будет залогом практически 100% успеха. Плюс внимательность!
Задачи на скорость в присутствии ускорения
Задачки на равноускоренное движение. Этот тип задач чуть сложнее. В дело вступает ускорение. Что такое ускорение? Это уже, в свою очередь, быстрота изменения скорости. Обозначается буквой а.
Обычно большая часть величин для решения такой задачи дана или выводится из нехитрой формулы:
V = Vo + аt, где V – скорость, а – ускорение, t – время движения.
В отличие от равномерного движения тело тут перемещается равноускоренно. Т.е. за каждый интервал времени скорость изменяется на одинаковую величину. Это применимо, например, к свободному падению с высоту. Пусть всё тот же мотоциклист едет первый час со скоростью 40 км/ч, а потом разгоняется до 60 км/ч и дальше ускоряется на 20 км/ч каждый час.
Опять-таки, все задачи тут завязаны на “кручу верчу обмануть хочу”. И да, на всякий случай отмечу, что все наши рассуждения из пунктов 1 и 2 тут тоже применимы, а ещё ускорение может получиться отрицательным и это не должно вас пугать.
Для решения задач из данной категории вам потребуется внимательно читать условие задачи и включить логику.
Задачки на среднюю скорость
Задачки на среднюю скорость. Тоже очень просто решаются. Что такое средняя скорость – это скорость, полученная как среднее арифметическое от скоростей на каждом из участков.
V средняя = Весь путь (S1+S2+S3+…) / всё время (t1+t2+t3+…)
Ну а дальше опять комбинаторика :). Подставь-посчитай-вырази. Ловкость рук и внимательность.
Сразу отмечу, что когда мы обсуждаем скорость или ускорение в том разрезе, как мы его видели до сих пор, мы всегда подразумевали именно среднее значение величин. Или не совсем-таки среднее, но условно разбитое на удобное для вычисления количество участков. Усредненное если желаете. В жизни же всё немного иначе.
Речь идёт о том, что если вы представите реальное движение того же несчастного мотоциклиста (или любого другого тела), о котором мы уже много раз вспомнили, он не будет ехать равномерно. Он поедет с рваным ритмом. Там на светофоре постоял. Там перед ямой затормозил. Дальше мотобат его хлопнул, документы проверяет…Бед будет много! И всё это отражается на скорости и как следствие – на ускорении. Это значит, что он действительно может проехать за час свои 50 км, но при этом за полчаса он проедет не 25 км, как мы ожидаем, а всего лишь 10 км, а дальше нагонит разницу.
Если мы высчитываем интегральный или усредненный показатель, нам в принципе-то, фиолетово. Главное, чтобы цифры сошлись. Но если нам нужно определить значение в конкретный момент, то расчёты уже будут неточные. И тут…
задачки, где есть мгновенная скорость
Что такое мгновенная скорость?
Это скорость в конкретный момент времени. Берем мотоциклиста, смотрим на его траекторию. Тыкаем пальцем в любую точку и узнаем, что там скорость пусть 10 км/ч. А через 5 минут уже 70 км/ч. А ещё через 10 минут – опять 10 км/ч. И вовсе не 50 км/ч на всём участке. Или ещё лучше – рисуем график изменения его расстояния в зависимости от времени. По такому графику всегда можно найти мгновенную скорость.
Как подступиться к подобным задачкам?
Для начала мы вспомним, что скорость это – первая производная от функции изменения расстояния по времени. Ведь производная – это и есть скорость изменения величины.
Дальше нам нужна функция, по которой изменялось расстояние. Без неё ничего решить не выйдет. Ведь данных попросту нет.
Исходя из формы кривой у нас будет её уравнение. Дальше нужно его дифференцировать.
Также в этом разделе часто вылезает некоторое дельта R. Что это такое и почему оно в формуле? Это всего лишь то самое значение расстояния (ничтожно малое), пройденного телом, за время стремящееся к нулю.
Ну и да…Для решения задач теперь нужно учитывать, что скорость мгновенная. Больше ничего не меняется.
Задачки на скорость при движении по кривой или окружности
Ещё мы можем столкнуться с понятием угловой скорости.
Начнем с того, что определим, чем вообще ситуация при движении по окружности отличается от ситуации с движением по обычной траектории? По сути дела ничем, кроме того, что путь будет высчитываться относительно окружности – будем считать длину окружности или дуги по известным всем формулам и использовать приведенные ранее зависимости для нахождения скорости.
Это тот самый случай, про который я говорю что учить без понимания бессмысленно. Ведь по сути нам сейчас нужно запомнить только формулы, приведенные раннее, а для криволинейного движения всё высчитаем, опираясь на них и понимая суть вопроса.
Но ко всему этому добавится угловая скорость. Что это? При движении материальной точки по окружности у неё есть линейная скорость, а есть угловая. Смотрим картинку.
Линейная скорость обозначена V, а угловая W (омега). Линейная скорость – это та же скорость, что мы разобрали выше. Она же мгновенная в данном случае. Скорость материальной точки, направленна по касательной к траектории.
Угловая скорость – это то, насколько быстро вращается наш радиус R. Представьте себе часы со стрелками. Стрелка вращается с некоторой скоростью, или – изменяет угол с некоторой скоростью. Вот вам и угловая скорость 🙂 И всё! Считается вот так:
Видите, логика совершенно такая же, как мы рассматривали выше.
Соответственно, в задачках на угловую скорость нужно мыслить аналогично самому первому пункту в нашем гиде. Это просто обычная материальная точка (тело) которая перемещается по окружности. Отличается только траектория ,а в отдельную тему это выделяют попросту для удобства восприятия.
Также, если есть задачка на криволинейное движение, то нужно иметь представление о виде траектории движения тела. Если траектория сложная, то её разбивают на простые геометрические формы и суммируют результаты.
Если нужно сложить скорости
Ещё бывают случаи, когда нужно выполнять сложение скоростей. Например, сложить две скорости разных тел и найти результирующую. Или сложить скорости одного тела.
Опять-таки, бояться таких задачек не нужно!
Вся логика строится из навыка оперировать с векторами.
Скорость – это величина векторная. Значит и зарисовать её можно с помощью вектора определенной длины. Вектора скорости могут быть расположены в одной плоскости или в объеме.
Советую посмотреть вот этот ролик на моем канале
Если вектора скорости находятся в одной плоскости то всё совсем просто. Чаще всего решение сводится к операциям над прямоугольными треугольниками. Бывают и очень простые случаи – векторы скорости вообще направлены вдоль одной прямой. Уже неважно разно направлены они или сонаправлены.
Чуть сложнее ситуация, если векторы скорости расположены в объеме. Там мы приходим к единичным векторам. Ситуация более геморройная, но от того не более сложная.
———————-
Итак, друзья!
Я постарался изложить все основы, которые могут помочь вам разобраться с решением задач на скорость. Очень надеюсь, что материал вам поможет.
Писать и разбирать каждую задачку – это довольно объемная штука. Такое нужно рассматривать уже в формате индивидуальных занятий.
Если я забыл осветить что-то в статье или не полностью/непонятно раскрыл теорию вопроса – пожалуйста пишите об этом в комментариях и я дополню статью и отвечу на ваш вопрос :)…Давайте вместе сделаем полезный и полный мануал. Ещё можно спросить меня в социальных сетях прямо на страничке https://vk.com/inznan или на лицекниге https://web.facebook.com/inznan
Ну и ответьте пожалуйста на вопрос, нужны ли такие материалы на моем проекте:
15 мая 2014
Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.
На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.
Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.
Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:
[v={S}’={x}’left( t right)]
Точно так же мы можем посчитать и ускорение:
[a={v}’={{S}’}’={{x}’}’left( t right)]
Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.
Давайте посмотрим, как это работает при решении реальных задач.
Пример № 1
Материальная точка движется по закону:
[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.
Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.
[v={S}’={x}’left( 2 right)]
Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.
Давайте решать. В первую очередь, посчитаем производную:
[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
Нам требуется найти производную в точке 2. Давайте подставим:
[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]
[=-16+32-12+5=9]
Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.
Пример № 2
Материальная точка движется по закону:
[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?
Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.
В первую очередь, вновь ищем производную:
[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]
[{x}’left( t right)={{t}^{2}}-8t+19]
От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:
[{{t}^{2}}-8t+19=3]
[{{t}^{2}}-8t+16=0]
[{{left( t-4 right)}^{2}}=0]
[t-4=0]
[t=4]
Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.
Ключевые моменты
В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.
Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.
Смотрите также:
- Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
- ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
- Схема Бернулли. Примеры решения задач
- Комбинаторика в задаче B6: средний тест
- Как решать задачи про летающие камни?
- B4: счетчики на электричество
Содержание:
Равномерное прямолинейное движение:
Вы изучали равномерное прямолинейное движение, познакомились с понятием «скорость». Скалярной или векторной величиной является скорость? Каковы закономерности равномерного прямолинейного движения?
Вы знаете, что движение, при котором за любые равные промежутки времени тело проходит одинаковые пути, называется равномерным. В каком случае одинаковыми будут не только пути, но и перемещения?
Проделаем опыт. Проследим за падением металлического шарика в вертикальной трубке, заполненной вязкой жидкостью (например, густым сахарным сиропом) (рис. 43). Будем отмечать положение шарика через равные промежутки времени. Опыт показывает, что за равные промежутки времени, например за
Сделаем вывод. При равномерном прямолинейном движении тело за любые равные промежутки времени совершает одинаковые перемещения и проходит одинаковые пути.
В 7-м классе вы находили скорость равномерного движения тела как отношение пути к промежутку времени, за который путь пройден: 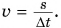
Скорость равномерного прямолинейного движения — это величина, равная отношению перемещения к промежутку времени, за который оно совершено:
Из равенства (1) следует, что скорость 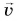
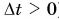
Отношение 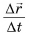
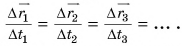
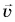
Из формулы (1) легко найти перемещение:
и путь 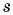
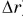
А как определить положение равномерно и прямолинейно движущегося тела в любой момент времени 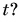
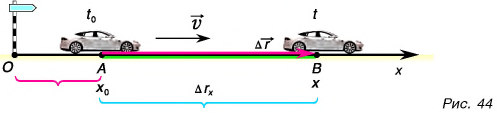
Автомобиль рассматриваем как материальную точку. Из формулы (2) находим проекцию перемещения автомобиля на ось Ох:
Согласно рисунку 44 за время 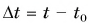
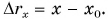
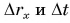
Приняв 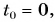
Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.
Зависимость координаты движущегося тела от времени называется кинематическим законом движения. Формула (5) выражает кинематический закон равномерного прямолинейного движения.
Для измерения скорости используются специальные приборы. В автомобилях имеется спидометр (рис. 45), на самолетах — указатель скорости. Эхолокаторы измеряют скорость тел, движущихся под водой, а радиолокаторы (радары) — в воздухе и по земле. Сотрудники службы дорожного движения с помощью портативного радара с видеокамерой (рис. 46) регистрируют скорость транспортных средств.
Для любознательных:
Скорости движения могут сильно отличаться. За одну секунду черепаха может преодолеть несколько сантиметров, человек — до 10 м, гепард — до 30 м, гоночный автомобиль — около 100 м.
Около 8 км за секунду пролетает по орбите спутник Земли (рис. 47). Но даже скорости космических кораблей «черепашьи» по сравнению со скоростью микрочастиц в ускорителях. В современном ускорителе (рис. 48) электрон за одну секунду пролетает почти 300 000 км!
Главные выводы:
- При равномерном прямолинейном движении за любые равные промежутки времени тело совершает одинаковые перемещения.
- Скорость равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.
- При равномерном прямолинейном движении тела модуль перемещения равен пути, пройденному за тот же промежуток времени.
- Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.
Пример решения задачи:
Кинематический закон прямолинейного движения лодки но озеру вдоль оси Ох задан уравнением 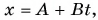
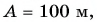
Определите: 1) проекцию скорости лодки 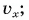
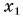
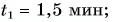
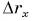
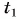
Решение
Сделаем рисунок к задаче.
По условию задачи координата лодки линейно зависит от времени. Значит, лодка движется равномерно. Сравнив 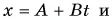
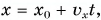
Найдем
Из рисунка 49: проекция перемещения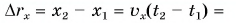
Ответ:
Графическое представление равномерного прямолинейного движения
Зависимости между различными величинами можно наглядно изобразить с помощью графиков. Использование графиков облегчает решение научных, практических задач и даже бытовых проблем.
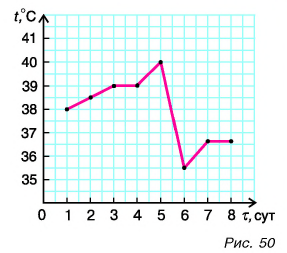
Например, по графику зависимости температуры пациента от времени (рис. 50) видно, что на 5-е сутки температура достигла своего максимума, затем резко упала, а еще через сутки стала приближаться к норме. График дал наглядное представление о течении болезни.
В физике роль графиков чрезвычайно велика. Умение строить и читать графики помогает быстрее и глубже понять физические явления.
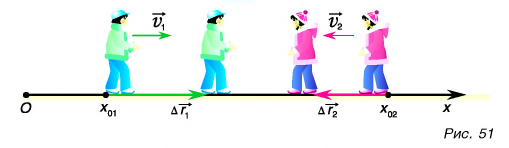
Рассмотрим простой пример из кинематики. Леша и Таня идут навстречу друг другу (рис. 51). Они движутся равномерно и прямолинейно. Модуль скорости Леши 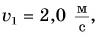
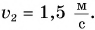
Выберем координатную ось Ох и зададим начальные положения участников движения (см. рис. 51). Пусть при 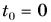
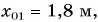
Построим графики зависимости проекции скорости 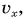
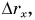
График проекции скорости
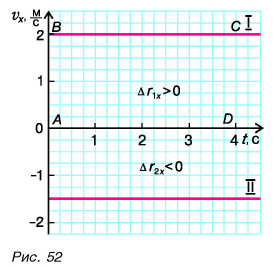
Согласно условию и рисунку 52 для проекций скорости движения Тани и Леши на ось Ох получим: 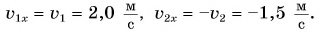
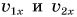
Графики показывают: проекция скорости при равномерном прямолинейном движении с течением времени не изменяется.
График проекции перемещения
Проекция перемещения 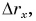
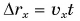
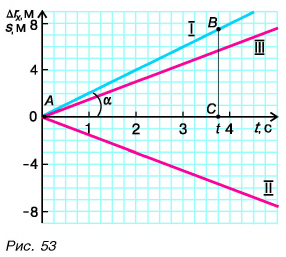
Зависимость проекции перемещения от времени для Леши 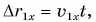
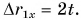
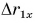
Для Тани 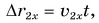
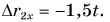
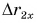
Из графиков и формул следует, что при равномерном прямолинейном движении проекция перемещения прямо пропорциональна времени.
График пути
Путь — величина положительная при любом движении тела. При равномерном прямолинейном движении путь равен модулю перемещения: 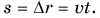
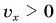
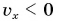
Графики пути показывают: при равномерном прямолинейном движении пройденный путь прямо пропорционален времени.
График координаты
Его называют также графиком движения.
По формуле 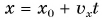
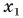
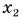
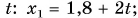
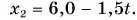
Графики движения показывают: при равномерном прямолинейном движении координата тела линейно зависит от времени.
По точке пересечения графиков I и II (точке А) (рис. 54) легко найти момент и координату места встречи Леши и Тани. Определите их самостоятельно.
Что еще можно определить по графикам?
По графику проекции скорости можно найти проекцию перемещения и пройденный путь
Рассмотрим прямоугольник ABCD на рисунке 52. Его высота численно равна 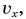
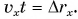
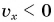
Докажите самостоятельно, что площадь между графиком проекции скорости и осью времени численно равна пройденному пути.
По углу наклона графика проекции перемещения можно оценить скорость движения
Рассмотрим треугольник АВС на рисунке 53. Чем больше угол наклона а графика проекции перемещения, тем больше скорость тела. Объясните это самостоятельно.
Главные выводы:
Для равномерного прямолинейного движения:
- График проекции скорости — прямая, параллельная оси времени.
- Графики проекции перемещения и координаты — прямые, наклон которых к оси времени определяется скоростью движения.
- Площадь фигуры между графиком проекции скорости и осью времени определяет проекцию перемещения.
Пример №1
Мотоциклист едет из города по прямолинейному участку шоссе с постоянной скоростью 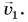
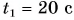
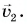
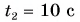
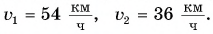
Решение
Изобразим координатную ось Ох, вдоль которой идет движение (рис. 55). Начало системы координат О свяжем с перекрестком.
В начальный момент времени мотоциклист находился на перекрестке, а велосипедист в точке В. Значит, кинематический закон движения мотоциклиста имеет вид:
Найдем координату 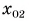
Тогда
Кинематический закон движения велосипедиста имеет вид:
Расстояние между мотоциклистом и велосипедистом через время 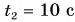
Пример №2
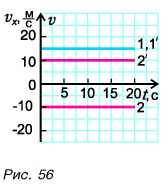
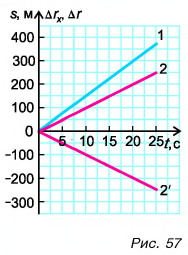
Построим графики проекций и модулей скорости. Для мотоциклиста графики проекции скорости 1 и модуля скорости 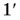
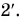
Графиками пути s, проекции 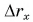
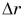
Для мотоциклиста:
Графики пути, модуля и проекции перемещения мотоциклиста совпадают (прямая 1).
Для велосипедиста:
Прямая 2 является графиком пути и модуля перемещения велосипедиста. Прямая 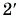
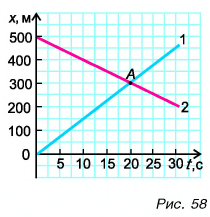
Графики координат представлены на рисунке 58. Они выражают зависимости 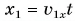
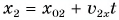
Ответ:
Прямолинейное равномерное движение и скорость
Из курса Физики VII класса вам известно, что равномерное прямолинейное движение является самым простым видом механического движения.
Прямолинейное равномерное движение — это движение по прямой линии, при котором материальная точка за равные промежутки времени совершает одинаковые перемещения.
При прямолинейном равномерном движении модуль и направление скорости с течением времени не изменяются:
Скорость при прямолинейном равномерном движении является постоянной физической величиной, равной отношению перемещения материальной точки ко времени, за которое это перемещение было совершено:
Так как отношение 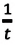
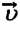
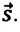
Если скорость 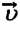
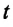
При прямолинейном равномерном движении пройденный телом путь равен модулю перемещения:
Так как уравнение в векторном виде можно заменить алгебраическими уравнениями в проекциях векторов, то для вычисления перемещения используют не формулу, выраженную через векторы, а формулу, содержащую в себе проекции векторов на координатные оси. При прямолинейном движении положение материальной точки определяется одной координатой X, определяются проекции векторов скорости и перемещения материальной точки на эту ось и уравнение решается в этих проекциях. Поэтому выражение (1.2) можно записать в проекциях перемещения и скорости на ось ОХ:
Можно получить формулу для вычисления координаты точки 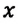
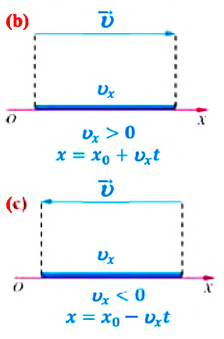
Выражение (1.5) является уравнением прямолинейного равномерного движения тела. Если материальная точка движется по направлению выбранной координатной оси ОХ, то проекция скорости считается положительной (b), если же движется против направления координатной оси, то проекция скорости считается отрицательной (с).
Из формулы (1.5) определяется выражение для проекции скорости:
Из формулы (1.6) становится ясным физический смысл скорости: проекция скорости на ось равна изменению проекции соответствующей координаты за единицу времени.
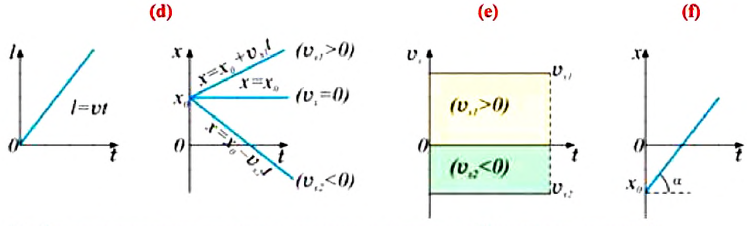
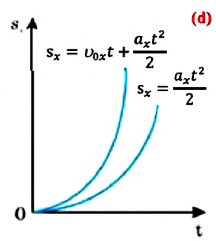
Пройденный путь и координата материальной точки при прямолинейном равномерном движении являются линейной функцией от времени (d). Скорость же является постоянной величиной, поэтому график скорость – время будет представлять собой линию, параллельную оси времени — скорость такого движения не зависит от времени (е):
График координата-время при равномерном движении образует определенный угол с осью времени. Тангенс этого угла равен проекции (модулю) скорости по оси ох (f):
Пример №3
Два велосипедиста одновременно начали движение навстречу друг другу вдоль прямой линии из пунктов А и В, расстояние между которыми 90 км. Скорость первого велосипедиста 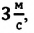
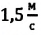
Определите: а) координату и время 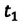
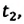
Дано:
Решение:
a) При решении задачи соблюдается следующая последовательность действий:
I действие. Выбирается система координат ОХ с началом координат в точке А и рисуется схема (h).
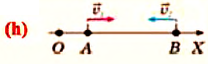
II действие. Уравнение движения записывается в общем виде:
III действие. На основании условия задачи уравнения движения велосипедистов записываются в общем виде:
IV действие. Координаты велосипедистов при встрече равны: 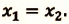
V действие. Для определения координат 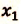
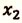
Так как 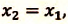
b) Так как по условию задачи велосипедисты движутся прямолинейно и без изменения направления движения, то пройденный путь равен проекции (модулю) перемещения:
c) Время 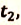
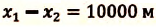
Скорость при равнопеременном прямолинейном движении
Из формулы (1.14) видно, что если известны ускорение 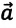
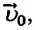
или ее проекцию на ось
Если начальная скорость равна нулю 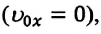
Из этих выражений видно, что скорость при равнопеременном движении является линейной функцией от времени. График зависимости скорости от времени – прямая линия, проходящая через начало координат (или через 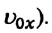
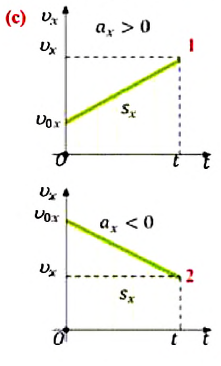
Перемещение при равнопеременном прямолинейном движении
Формулу для определения перемещения при равнопеременном движении можно вывести на основе графика скорость-время. Проекция перемещения равна площади фигуры между графиком 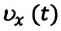
На приведенных графиках — это заштрихованная фигура трапеции (см: с):
или в векторной форме:
Если в последнюю формулу вместо 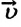
обобщенную формулу перемещения для равнопеременного движения:
Таким образом, формула проекции перемещения (например, на ось 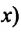
а формула координаты:
(1.23) является формулой перемещения при равнопеременном движении в векторной форме, а (1.24) и (1.25) обобщенными формулами координаты и проекции перемещения, соответственно. Если материальная точка начинает движение из состояния покоя 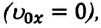
Как видно из формулы, проекция перемещения при прямолинейном равнопеременном движении пропорциональна квадрату времени 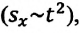
В некоторых случаях возникает необходимость определить перемещение материальной точки, не зная время 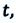
Это выражение подставляется в формулу (1.21):
После простых преобразований получаем:
Для проекции конечной скорости получаем: 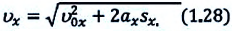
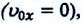
Равноускоренное и равнозамедленное движения
Равнопеременное движение по характеру может быть или равноускоренным, или же равнозамедленным.
При равноускоренном движении векторы 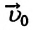
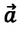
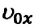
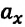
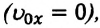
При равнозамедленном движении векторы 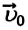
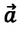
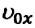
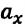
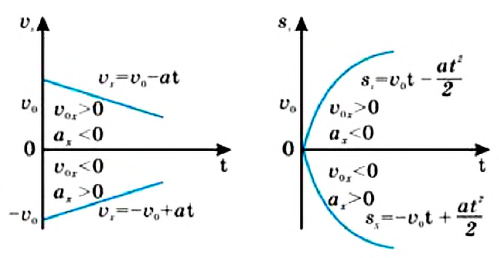
В таблице 1.3 даны формулы и соответствующие графики равноускоренного и равнозамедленного прямолинейного движения.
Таблица 1.3.
| Прямолинейное равноускоренное движение | |
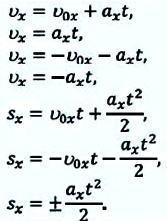 |
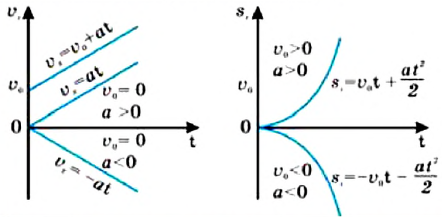 |
|
Примечание: так как Это соотношение иногда называется “правило путей”. |
|
| Прямолинейное равнозамедленное движение | |
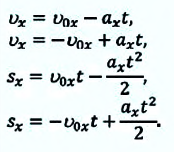 |
|
Кинематика прямолинейного движения
Физические величины бывают скалярные и векторные. Скалярные физические величины характеризуются только численным значением, тогда как векторные определяются и числом (модулем), и направлением. Скалярными физическими величинами являются время, температура, масса, векторными — скорость, ускорение, сила.
Мир вокруг нас непрерывно изменяется, или движется, т. е. можно сказать, что движение (изменение) есть способ существования материи.
Простейшая форма движения материи — механическое движение — заключается в изменении взаимного расположения тел или их частей в пространстве с течением времени. Наука, изучающая механическое движение, называется механикой (от греческого слова 
Даже самое простое движение тела оказывается достаточно сложным для изучения и исследования. Соответственно, для того чтобы в сложном явлении «увидеть» главное, в физике строится его адекватная упрощенная модель.
В механике широко используется простейшая модель реального тела, называемая материальной точкой (МТ). Под материальной точкой понимают тело, размерами и формой которого можно пренебречь при описании данного движения. Хотя МТ представляет собой абстрактное понятие, упрощающее изучение многих физических явлений, она, подобно реальному телу, «имеет» массу, энергию и т. д.
Кроме материальной точки, в механике используется модель абсолютно твердого тела. Под абсолютно твердым телом понимают модель реального тела, в которой расстояние между его любыми двумя точками остается постоянным. Это означает, что размеры и форма абсолютно твердого тела не изменяются в процессе его движения. В противном случае говорят о модели деформируемого тела.
В классической (ньютоновской) механике рассматривается движение тел со скоростями, намного меньшими скорости света в вакууме
Классическая механика состоит из трех основных разделов: кинематики, динамики и статики. В кинематике (от греческого слова 
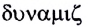
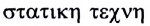
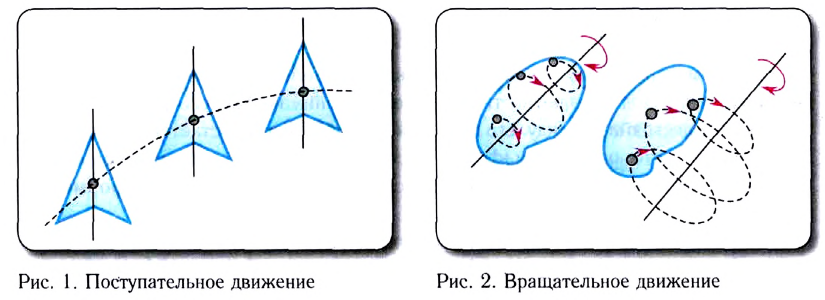
Всякое движение тела можно представить в виде двух основных видов движения — поступательного и вращательного.
Поступательным называется движение тела, при котором прямая, соединяющая в этом теле любые две точки, при перемещении остается параллельной самой себе (рис. 1).
Вращательным называется движение абсолютно твердого тела вокруг неподвижной прямой, называемой осью вращения, при котором все точки тела движутся по окружностям, центры которых лежат на этой оси (рис. 2).
Основными задачами кинематики являются:
описание совершаемого телом движения с помощью математических формул, графиков или таблиц;
определение кинематических характеристик движения (перемещения, скорости, ускорения).
Движение тела можно описать только относительно какого-либо другого тела. Тело, относительно которого рассматривается исследуемое движение, называют телом отсчета (ТО). Для описания движения используются формулы, графики и таблицы, выражающие зависимость координат, скоростей и ускорений от времени.
Основным свойством механического движения является его относительность: характер движения тела зависит от выбора системы отсчета (СО).
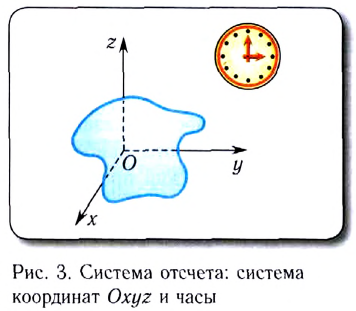
Систему отсчета, выбираемую для описания того или иного движения, образуют: тело отсчета, связанные с ним система координат (СК) и прибор для измерения времени (часы) (рис. 3).
Система координат и часы необходимы для того, чтобы знать, как с течением времени изменяется положение тела относительно выбранного тела отсчета.
Для описания движения материальной точки в пространстве вводятся такие понятия, как траектория, перемещение, путь.
Линию, которую описывает материальная точка в процессе движения по отношению к выбранной СО, называют траекторией (от латинского слова trajectorus — относящийся к перемещению). Если траектория является прямой линией, то движение называется прямолинейным, в противном случае — криволинейным.
Длина участка траектории, пройденного МТ в процессе движения, называется путем (s).
Термин «скаляр», происходящий от латинского слова scalarus — ступенчатый, введен У. Гамильтоном в 1843 г.
Термин «вектор» произошел от латинского слова vector — несущий и введен У. Гамильтоном в 1845 г.
Перемещением называют вектор 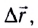
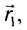
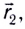
Для количественного описания механического движения тел (МТ) вводятся физические величины, характеризующие пространство и время: длина l, время t.
Длина l определяется как расстояние между двумя точками в пространстве. Основной единицей длины в Международной системе единиц (СИ) является метр (1м).
Время t между двумя событиями в данной точке пространства определяется как разность показаний прибора для измерения времени, например часов. В основе работы прибора для измерения времени лежит строго периодический физический процесс. В СИ за основную единицу времени принята секунда (1с).
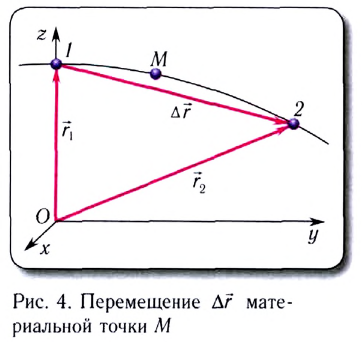
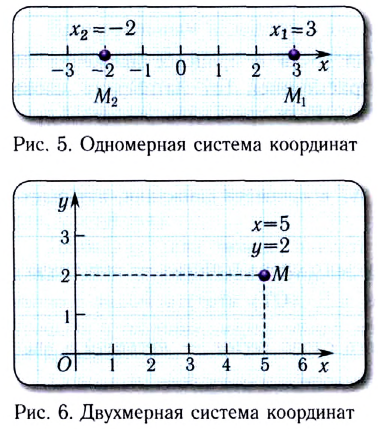
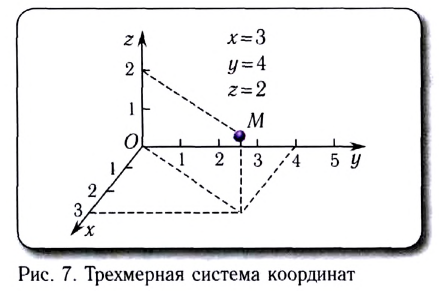
В зависимости от вида движения могут выбираться следующие системы координат: одномерная (на прямой линии) (рис. 5), двухмерная (на плоскости) (рис. 6), трехмерная (в пространстве) (рис. 7).
Произвольное движение материальной точки может быть задано одним из трех способов: векторным, координатным, траекторным (естественным).
При векторном способе описания положение движущейся МТ по отношению к выбранной системе отсчета определяется ее радиус-вектором
Радиус-вектор 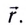
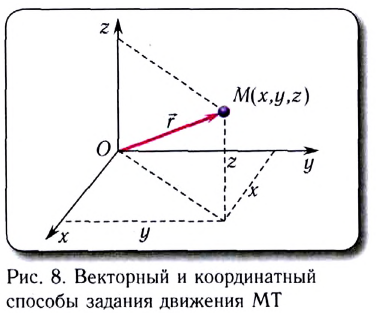
При координатном способе описания положение точки относительно СО определяется координатами х, у, z, а закон движения — уравнениями х = х(t), у = y(t), z = z(t) (см. рис. 8). Исключив из этих уравнений время /, можно найти уравнение траектории движения точки.
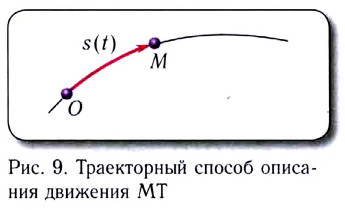
Траекторный (естественный) способ описания движения применяется, когда известна траектория движения материальной точки по отношению к выбранной СО (рис. 9).
Текущее положение материальной точки в данном случае определяется расстоянием s, измеренным вдоль траектории от выбранного на ней начала отсчета (точка О на рисунке 9). Кинематический закон движения МТ при этом задается уравнением s = s(t).
Если положить в основу классификации движений характер изменения скорости, то получим равномерные и неравномерные движения, а если вид траектории, то — прямолинейные и криволинейные.
Для того чтобы описать быстроту изменения положения тела (МТ) и направление движения относительно данной СО, используют векторную физическую величину, называемую скоростью
Чтобы охарактеризовать неравномерное движение тела (МТ), вводят понятие средней скорости 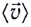
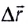
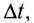
Средней путевой скоростью 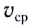
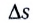
Средняя путевая скорость 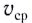
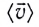
Однако средняя скорость 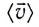
Для того чтобы отразить характер движения в данной точке траектории или в данный момент времени, вводится понятие мгновенной скорости 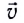
Вектор мгновенной скорости 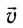
В СИ основной единицей скорости является метр в секунду
Простейший вид движения — равномерное. Равномерным называется движение МТ, при котором она за любые равные промежутки времени совершает одинаковые перемещения.
При прямолинейном движении в одном направлении модуль перемещения 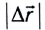
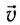
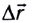
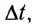
При равномерном движении скорость постоянна 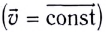
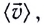
Зависимость перемещения от времени имеет вид 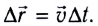
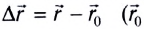
момент времени 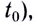
При проецировании радиус-вектора, например, на ось Ох получаем кинематическое уравнение для координаты при равномерном движении:
Здесь 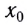
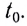
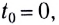
Для наглядности описания механического движения удобно представлять зависимости между различными кинематическими величинами графически.
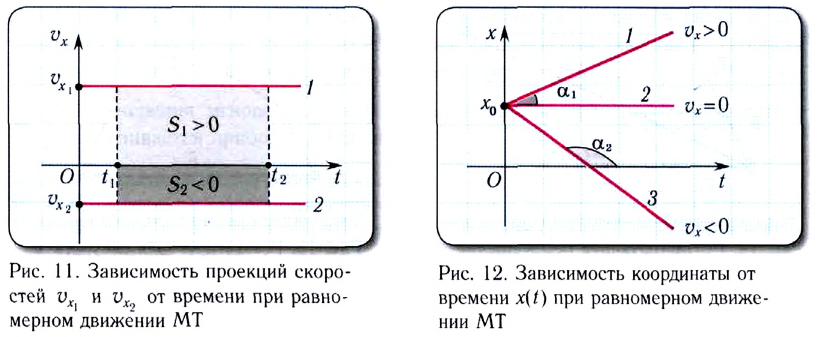
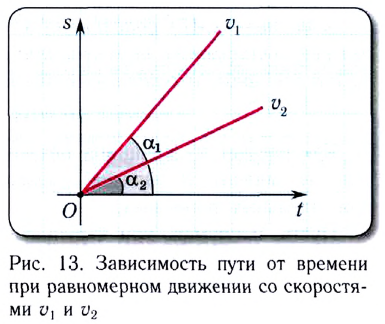
Скорость МТ при равномерном движении постоянна, поэтому график зависимости проекции скорости 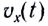
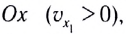
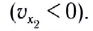
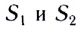
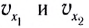
График зависимости координаты материальной точки, движущейся равномерно прямолинейно, от времени x(t) — линейная функция (рис. 12).
На рисунке отрезок / прямой соответствует равномерному движению в положительном направлении оси Ох; отрезок 2 прямой — покою материальной точки; отрезок 3 прямой — равномерному движению в отрицательном направлении оси Ох.
Проекция скорости движения численно равна угловому коэффициенту этой прямой линии:
т. е. тангенсу угла наклона (tga) этой прямой к оси времени.
График зависимости пути (модуля перемещения|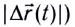
Угловой коэффициент (tga) этой прямой численно равен модулю скорости движения v. Поэтому на рисунке большей скорости у, соответствует больший угловой коэффициент (tg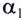
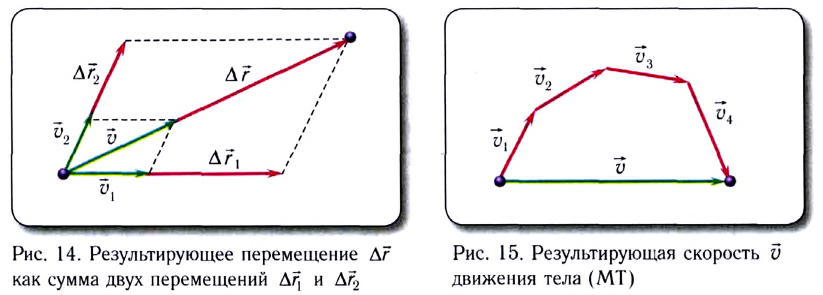
Для тел (МТ), участвующих в нескольких движениях одновременно, справедлив принцип независимости движений:
если тело (МТ) участвует в нескольких движениях одновременно, то его результирующее перемещение равно векторной сумме перемещений за то же время в отдельных движениях:
Как следует из принципа независимости движений, конечное перемещение тела не зависит от порядка (последовательности) суммирования перемещений при отдельных движениях.
Пусть, например, при переправе через реку, скорость течения которой 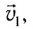
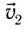
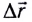
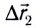
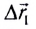
- Заказать решение задач по физике
На основе принципа независимости движений формулируется классический закон сложения скоростей:
результирующая скорость 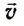
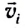
Этот закон справедлив только при условии, что скорость каждого отдельного движения мала по сравнению со скоростью света
Так, для рассмотренного примера (см. рис. 14) результирующая скорость лодки
Равномерное движение по прямой линии в повседневной жизни встречается сравнительно редко. Например, различные транспортные средства (автомобиль, автобус, троллейбус и т. д.) равномерно и прямолинейно движутся лишь на небольших участках своего пути, в то время как на остальных участках их скорость изменяется как по величине, так и по направлению.
Для измерения мгновенной скорости движения на транспортных средствах устанавливается прибор — спидометр.
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Ускорение в физике
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
- Путь и перемещение



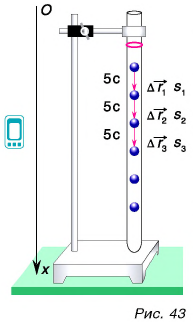
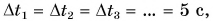




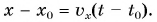




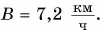
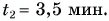


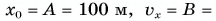
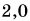
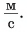
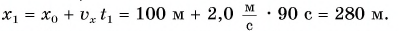
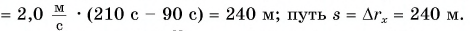
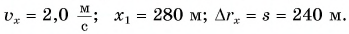
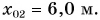
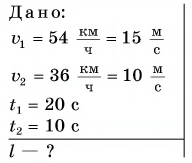

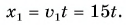
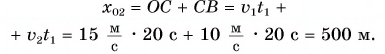
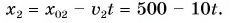
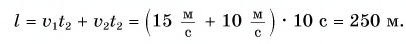
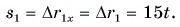
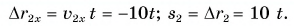
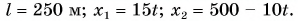
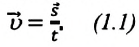
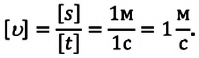

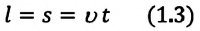
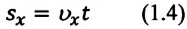
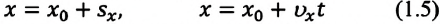
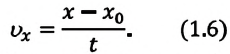
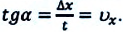
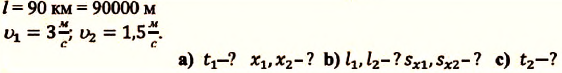
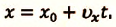
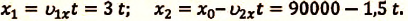
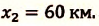
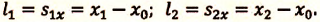
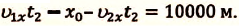
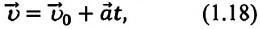
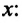
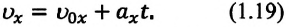

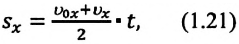
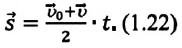
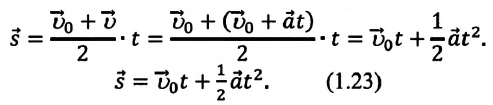
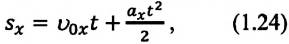
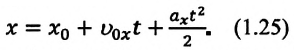
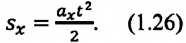
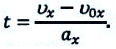
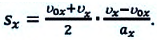

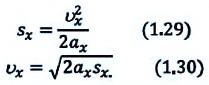
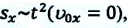 то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени:
то отношение проекций перемещения равно отношению квадратов соответствующих промежутков времени: