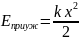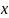Как найти скорость маятника после удара

Федеральное
агентство по образованию

Государственное
образовательное учреждение высшего
профессионального образования

«НАЦИОНАЛЬНЫЙ
ИИСЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ
ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Новокузнецкий
филиал

Кафедра
естественнонаучных и общепрофессиональных
дисциплин

Отчет по лабораторной работе по физике измерение скорости пули с помощью баллистического маятника

Выполнил
____________ А.Уваров, М. Масалимов

(подпись)

студенты
гр. 5Б10НК,
курс 1________

(дата)

Проверила

Доцент
кафедры ЕНПД _________
А.Н. Антоненко

(подпись)

______________

Новокузнецк,
2011

1.1.Задание

Измерение скорости пули с помощью
баллистического маятника.

1.2.Цель работы

Ознакомиться
с одним из примеров применения законов
сохранения импульса и механической
энергии при решении баллистических
задач. С помощью баллистического маятника
определить скорости пуль с различными
массами.

1.3.Учебно-исследовательское
оборудование

Модульный
учебный комплекс МУК-М1: рабочий узел
«баллистический маятник», набор пуль
с разными массами.

1.4. Краткое
теоретическое введение

Баллистический
маятник представляет собой массивный
цилиндр массой М,
который подвешен на невесомых и
нерастяжимых нитях так, что он может
двигаться только поступательно. В
цилиндр в горизонтальном направлении
производят выстрел пулей массы т
из пружинного пистолета, неподвижно
закрепленного вблизи маятника. Если
торцевая стенка цилиндра изготовлена
из мягкого и легко деформируемого
материала, например, пластилина, то пуля
при попадании может испытывать абсолютно
неупругий удар. Абсолютно
неупругий удар
– это удар, при котором потенциальная
энергия упругой деформации не возникает;
кинетическая энергия тел частично либо
полностью превращается во внутреннюю
энергию; после удара тела двигаются с
одинаковой скоростью (т.е. как единое
тело) либо покоятся. При таком ударе
выполняется только закон сохранения
импульса, закон же сохранения механической
энергии не соблюдается – механическая
энергия частично или полностью переходит
во внутреннюю.

Если
зарядить пистолет пулей, то в сжатой
при этом пружине будет запасена
потенциальная энергия:

, (1)

где
k
– коэффициент упругости,

x
– деформация пружины.

Предположим,
что вся энергия сжатой пружины при
выстреле полностью превращается в
кинетическую энергию пули. Это означает,
что мы пренебрегаем потерями энергии
на преодоление трения между пулей и
стволом пистолета и на сообщение
кинетической энергии самой пружине.
Учтем, кроме того, что геометрические
размеры всех пуль одинаковы, а, значит,
одинакова деформация для любой пули,
и, следовательно, одинакова запасаемая
пружиной потенциальная энергия. Тогда
из закона сохранения механической
энергии следует, что пули различных
масс, вылетая из пружинного пистолета,
должны иметь одинаковые кинетические
энергии:

, (2)

где
v
– скорость пули после выстрела,

– масса
пули,кг,

– коэффициент
упругости,

–
деформация пружины.

Из
(2) получаем зависимость скорости пули
после выстрела от ее массы:

, (3)

где

– масса пули,кг,

– коэффициент
упругости,

–
деформация пружины.

Поскольку
величины x
и
k
для
всех пуль одинаковы, то график ожидаемой
зависимости скорости пули


от

,
должен, согласно формуле (3), представлять
собой прямую линию, проходящую через
начало координат.

Пролетев
небольшое расстояние между пистолетом
и маятником, пуля входит в пластилин,
заполняющий
цилиндр, и за счет вязкого трения быстро
теряет скорость. При этом часть
механической энергии пули расходуется
на неупругую деформацию и превращается
во внутреннюю энергию пластилина и
пули, то есть пластилин и пуля нагреваются.

Процесс
удара является кратковременным. Если
масса маятника велика по сравнению с
массой пули (M>>m),
то за время удара он в силу своей
инерционности не успевает выйти из
положения равновесия. Это позволяет
считать систему маятник-пуля в момент
удара замкнутой в горизонтальном
направлении, так как сила тяжести и сила
натяжения подвеса направлены вертикально
при вертикальном положении маятника.
Для замкнутой системы можно применить
закон сохранения импульса:

, (4)

где

– скорость пули до удара (при этом скорость
маятника равна нулю), м/с²,

u
– скорость, приобретенная системой
маятник-пуля сразу после удара, м/с^2,

–
масса маятника, кг,

– масса
пули, кг.

Маятник
вместе с пулей, получив за счет неупругого
удара импульс, отклоняется от положения
равновесия на угол α.
В
процессе отклонения на маятник действует
сила тяжести (вниз) и сила упругости
подвеса (перпендикулярно направлению
мгновенной скорости маятника). Если
пренебречь потерями энергии на трение
в подвесе и на сопротивление воздуха,
то работу при отклонении маятника
совершает только гравитационная сила.
Это позволяет воспользоваться
законом сохранения механической энергии:

, (5)

где
h
– наибольшая высота, м,

–
масса маятника, кг,

– масса
пули, кг,

–
ускорение свободного падения,
м/с²,

– скорость,
приобретенная системой маятник-пуля
сразу после удара, м/с².

Слева
в этой формуле кинетическая энергия
при поступательном движении маятника
сразу после удара (в этой точке
потенциальную энергию принимаем равной
нулю), а справа – потенциальная энергия
системы в момент ее остановки на высоте
h.

Решая
совместно (4) и (5) получим

, (6)

где

– масса маятника, кг,

– масса
пули, кг,

–
ускорение свободного падения,
м/с²,

– длина нити подвеса, м.

рис.
2

h
– наибольшая высота, на которую
поднимается маятник.

Таким
образом, найдя значение высоты подъема
маятника можно рассчитать скорость
полета пули.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Баллистический маятник

#683
2009-06-21 11:51 GMT

Пуля массой 10г. ударяется в баллистический маятник и застревает в нём. Найти скорость пули, если маятник в результате соударения отклонился на 30 градусов, длина нити 90см., масса маятника 5кг.

#706
2009-08-24 12:55 GMT

m=0,01 кг, M=5 кг, l=0,9 м (длина маятника), g=9,8 м/с*с.

до соударения общая энергия состояла из кинетической энергии пули – m*v*v/2,

после соударения маятник отклонился на 30 градусов, т.е. поднялся на высоту h=l*(1-cos30) и ситема приобрела потенциальную энергию (m+M)*g*h=m*V*V/2,

откуда

V=корень кв. от (2*(m+M)*g*l*(1-cos30)/m)~34,75 м/с

#1951
2010-05-07 17:20 GMT

Вообще-то закон сохранения не выполняется, т.к. при столкновении часть энергии пули перешла во внутреннию энергию, т.е. в нагрев.

Закон сохранения ‘энергии можно применить для нахождения начальной скорости маятника вместе с пулей, т.е. (m+M)*g*h=(m+M)*V*V/2, отсюда V=корень квадратный (2*g*h) – это скорость маятника с пулей после соударения. а вот начальную скорость пули можно найти из закона сохранения импульса: m*Vo=(m+M)*V, откуда Vo=(m+M)*V/m.

подставляя V и h получим ответ: Vo=(m+M)*корень_квадратный_[ 2*g*l*(1-cos30 )] / m ~ 768 м/с

#1976
2010-05-11 12:21 GMT

#4944
2011-02-28 12:02 GMT

баллистического маятника

Цель работы: Определение скорости
пули с помощью баллистического маятника с использованием законов сохранения
импульса и энергии.

Приборы и принадлежности: баллистический маятник,
шкала, пружинный пистолет, линейка и пули.

Теоретическое введение

Из
практики известно, что скорость полета пули достигает значительной величины.
Поэтому прямое измерение скорости, т.е. определение времени, за которое пуля
проходит известное расстояние, требует специальной аппаратуры. Много проще
измерять скорость пули косвенными методами, среди которых широко
распространены методы, использующие неупругие соударения, т.е. соударения, в
результате которых столкнувшиеся тела соединяются вместе и продолжают
движение как одно целое.

Пусть летящая пуля испытывает неупругий удар со свободным неподвижным
телом значительно большей массы. После удара тело начинает двигаться, причем
скорость его во столько раз меньше скорости пули, во сколько раз масса пули
меньше массы тела. (Этот результат можно получить с помощью закона сохранения
импульса). Если теперь измерить сравнительно небольшую скорость тела, то
легко можно вычислить и скорость полета пули.

К числу методов, основанных на этой идее, относится и метод
баллистического маятника. В данной работе для определения скорости пули
использованы законы сохранения импульса и полной механической энергии.

Описание рабочей установки и
метода измерений

Баллистический
маятник представляет собой тяжелое тело массой М, подвешенное на двойном бифилярном подвесе (рис.1). Когда после
выстрела пуля попадает в это тело, то оно отклоняется от положения
равновесия.

Пренебрегая сопротивлением воздуха, к системе «маятник-пуля» можно
применить закон сохранения импульса, который в проекции на ось x запишется

где mυ – проекция импульса на
ось x до взаимодействия;

(М+m)U –проекция
импульса системы (пуля +маятник) на ось x неупругого удара.

Закон сохранения
импульса: в изолированной системе тел 
сумма импульсов взаимодействующих тел остается постоянной во времени,
т.е. .

Закон сохранения механической энергии: в изолированной системе тел,
где действуют только консервативные силы, полная механическая энергия
(кинетическая плюс полная потенциальная энергии) остается постоянной, т.е. Е=Е_к+Е_п=const.

При ударе пули маятник вместе с пулей приобретает кинематическую
энергию, равную после соударения

Маятник с пулей приходит в движение, отклоняется на некоторый угол от
вертикали, и центр масс системы «маятник-пуля» поднимается на некоторую
высоту h
(рис.2).

Если
пренебречь трением в подвесе маятника и сопротивлением воздуха, то можно
рассматривать систему «маятник-пуля» как изолированную, консервативную и
применять к ней закон сохранения полной механической энергии.

В
момент наибольшего отклонения маятника его кинетическая энергия Е_к
полностью превратится в потенциальную энергию силы тяжести

где g
– ускорение свободного падения тела.

Тогда

Подставив (5) в (2), найдем выражение для скорости пули

Следовательно, скорость пули можно вычислить, если измерить высоту
подъема h
центра масс маятника. Однако измерение h довольно сложно. Его можно
заменить более простым измерением горизонтального перемещения S, которое определяют по неподвижной
шкале.

Если после соударения маятник отклонился на небольшой угол (рис.2), то
можно считать, что центр масс маятника перемещается вдоль хорды АВ. Тогда из подобия треугольников АКВ и ОАС можно записать отношение

где ВК = S– горизонтальное
смещение маятника; АК = h, ОС^АВ.

При малом отклонении S и
достаточной длине подвеса l (S<<l) можно положить, что

 и

Тогда соотношение (6) можно записать в виде

 или

Поставив (7) в (5), получим формулу для скорости пули:

Формула (8) является расчетной. Определяя величины M,
m, S, l,
экспериментально, по формуле (7) можно определить скорость пули υ.

Ход работы

1.     
Привести маятник в состояние равновесия и подвесить шкалу под
указатель маятника.

2.     
Произвести 5 – 6 выстрелов, каждый раз отмечая смещения указателя по
шкале. Результаты измерений записать в таблицу.

3.     
Вычислить скорость пули по формуле (8).

4.     
Вычислить абсолютную погрешность измерения S по формуле:

где t_p(n)– коэффициент Стьюдента для доверительной
вероятности p
= 0,95 и числа измерений n.

5.     
Вычислить относительную погрешность измерения скорости

6.     
Найти абсолютную погрешность

7.     
Результаты измерения записать в виде

– средние величины.

m = 9,6 г; М =296 г; l = 193 см.

Таблица

№	S	<S>	DS	M	m	l	g	<υ>	Dυ	E
	м	м	м	кг	кг	М	м/с2	м/с	м/с	%

Вопросы для допуска

1.     
Изложите цель работы, назначение приборов и принадлежностей.

2.     
Опишите рабочую установку и ход эксперимента.

3.     
Какие допущения возможны, если рассматривать систему «маятник-пуля»
как замкнутую?

4.     
Напишите рабочую формулу, примененную в данной работе.

5.     
Какие законы Вы использовали для получения расчетной формулы для
скорости пули?

6.     
Оцените погрешность метода измерений.

7.     
Как в установке обеспечить условия, при которых удар пули в маятник
можно считать неупругим, центральным и прямым?

8.     
Какие допущения делаете, используя закон сохранения механической
энергии в форме, выраженной формулой (9)?

Вопросы для защиты работы

1.     
Что называется импульсом тела (количеством движения) и в каких
единицах он измеряется в системе СИ?

2.     
При каком условии систему «маятник-пуля» можно рассматривать как
изолированную?

3.     
В чем состоит закон сохранения импульса? К каким системам он применим?
Дайте вывод этого закона и приведите примеры его проявления (его действия).

4.     
Как найти изменение импульса неизолированной системы?

5.     
Какие существуют виды механической энергии. Дайте их определения.

6.     
Для каких систем справедлив закон сохранения механической энергии и
как он формулируется?

7.     
Выведите формулу кинетической энергии.

8.     
Выведите расчетную формулу.

9.     
Какой удар называют абсолютно упругим и какой
неупругим?

10.  Объяснить происхождение
систематических и случайных ошибок, встречающихся в данной работе.