$begingroup$
A neutron star has radius $10$km and mass $2.5times 10^{29}$kg. A meteorite is drawn into its gravitational field. Calculate the speed with which it will strike the surface of the star. Neglect the initial speed of the meteorite.
In the solution provided, we use the formula for escape speed, which is
$$v = sqrt{frac{2GM}{R}}$$
But the derivation of the formula for escape speed involves a mass has zero kinetic energy and zero gravitational potential energy.
So, my question is: Why can we use escape speed to calculate striking of a meteor in this case?
asked Jul 14, 2016 at 3:35
$endgroup$
$begingroup$
This is a classic example of the conservation of total energy. The meteor is assumed to have zero kinetic energy sufficiently far away from the black hole and the gravitational potential there is zero, as well. As the meteor gains kinetic energy while falling toward the black hole the gravitational energy increases in direct proportion (though the latter is negative so the sum does not change). When reaching the surface of the black hole the meteor’s kinetic energy is equal to the potential energy there, as well.
$$1/2mv^2 = MG/R $$
Turning the problem around, you have the (escape) velocity required to get the meteor unbound from the black hole’s gravitational potential.
answered Jul 14, 2016 at 5:05
$endgroup$
1
С какой скоростью метеорит падает на землю
«Падающие звезды» – такое поэтичное название придумали люди для метеорных тел, захваченных гравитацией Земли и попадающих в ее атмосферу. Дальнейшая судьба метеорных тел определяется их размером: самые маленькие сгорают в атмосфере, более крупные достигают земной поверхности.
Любое небесное тело, превышающее по размерам космическую пыль, но уступающее астероиду, называют метеороидом. Попавший в земную атмосферу метеороид именуется метеором, а упавший на земную поверхность – метеоритом.
Скорость метеороидных тел, движущихся в космическом пространстве, может быть различной, но в любом случае она превышает вторую космическую скорость, равную 11,2 км/с. Такая скорость позволяет телу преодолевать гравитационное притяжение планеты, но она присуща лишь тем метеорным телам, которые родились в Солнечной системе. Для метеороидов, которые прилетают извне, характерны и более высокие скорости.
Минимальная скорость метеорного тела при встрече с планетой Земля определяется тем, как соотносятся направления движения обоих тел. Минимальная сопоставима со скоростью движения Земли по орбите – около 30 км/с. Это относится к тем метеороидам, которые движутся в том де направлении, что и Земля, как бы догоняя ее. Таких метеорных тел большинство, ведь метеороиды возникли из того же вращающегося протопланетного облака, что и Земля, следовательно, должны двигаться в том же направлении.
Если метеороид движется навстречу Земле, то его скорость прибавляется к орбитальной и потому оказывается более высокой. Скорость тел из метеорного потока под названием Персеиды, через который Земля каждый год проходит в августе, равна 61 км/с, а метеороиды из потока Леонид, с которым планета встречается между 14 и 21 ноября, имеют скорость 71 км/с.
Наибольшая скорость характерна для фрагментов комет, она превышает третью космическую – такую, которая позволяет телу покинуть пределы Солнечной системы – 16,5 км/с, к которой нужно прибавить и орбитальную скорость, и сделать поправки на направление движения относительно Земли.
В верхних слоях атмосферы воздух почти не препятствует движению метеора – он здесь слишком разрежен, расстояние между молекулами газа может превышать размеры среднего метеорного тела. Но в более плотных слоях атмосферы на метеор начинает воздействовать сила трения, и движение его замедляется. На высоте 10-20 км от земной поверхности тело попадает в область задержки, теряя космическую скорость и как бы зависая в воздухе.
В дальнейшем сопротивление атмосферного воздуха уравновешивается земной силой тяжести, и метеор падает на поверхность Земли подобно любому другому телу. Скорость его при этом достигает 50-150 км/с, в зависимости от массы.
Не всякий метеор достигает земной поверхности, становясь метеоритом, многие сгорают в атмосфере. Отличить метеорит об обычного камня можно по оплавленной поверхности.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,944 -
разное
16,904
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Прежде всего нужно сказать, что метеориты падают на нашу планету постоянно. Ученые говорят, что на Землю падает порядка 5-6 тонн космических тел каждые сутки. Как правило они сгорают в верхних слоях атмосферы. Поверхности Земли могут достичь только относительно большие метеориты.
К слову, все космические тела, которые вошли в атмосферу Земли и там сгорели нельзя считать метеоритами, это метеоры и болиды. Метеорит – это космическое тело, которое достигло поверхности планеты. И они могут иметь массу от нескольких рам до десятков тонн. Самый большой метеорит, найденный на Земле имеет массу порядка 60 тонн – метеорит Гобба.
А теперь непосредственно о скорости падения метеорита
Астрофизики говорят, что метеориты при входе в атмосферу Земли могут иметь скорость своего движения от 11,2 до 72 километров в секунду. Отмечу что нижний предел скорости, это вторая космическая скорость, а максимум это 42 километра в секунду, но здесь нужно добавить орбитальную скорость вращения нашей планеты что и даст 72 километров в секунду.
Даже на средней скорости падения метеорита в 25 километров в секунду и массе в несколько сотен тонн, он может сгореть дотла или же достигнет поверхности Земли с массой в несколько килограмм или грамм. При этом в атмосфере можно наблюдать четкие следы сгорания.
Кроме горения, атмосфера Земли существенно замедляет метеорит. При замедлении снижается и скорость горения космического тела. В таком случае они падают не Землю не раскаленными, а теплыми. В атмосфере большие метеориты могут разрываться на мелкие части, после чего образуется метеоритный дождь. Самый известный метеорит, который разорвался над поверхностью Земли является Тунгусский болид.
В момент столкновения метеорита с землей он имеет скорость порядка 2-4 километров в секунду. При ударе выделяется колоссальное количество энергии, что может сопровождаться взрывом. На месте падения крупных тел образуются кратеры круглой формы.
В настоящий момент нет информации о прямом попадании метеорита в человека. Но есть данные о двух случаях, когда метеорит отрикошетил и ударил человека.
Жмите палец вверх и подписывайтесь на канал Kvant
Попытка оценить размер метеорита, упавшего сегодня на Урале.
На основании реакций камер видеорегистраторов (см. http://chel.kp.ru/online/news/1367309/), пиковая освещённость в момент вспышки составляет порядка 300 тыс. люкс. По свидетельствам очевидцев, многие получили загар на лице, что говорит о существенном ультрафиолетовом избытке, откуда можно предположить, что на видимую область пришлось не более половины светового излучения. Принимая расстояние до вспышки 15 км, получим мощность 2.5∙1012 Вт. Продолжительность вспышки — около 3 секунд, значит энергия, перешедшая в излучение порядка 7.5∙1012 Дж. Если кинетическая энергия вдвое больше, то для скорости 10 км/с получаем оценку массы 300 тонн. В зависимости от плотности метеорита, получаем оценку его размера от 4 (железо) до 20 (метановый снег) метров.
А тротиловый эквивалент взрыва получается почти 4 килотонны…
UPDATE Я сохранил ролик (http://youtu.be/gQ6Pa5Pv_io) локально, чтобы разобрать его на кадры и измерить.
Итак: между вспышкой (4:40)и приходом звука (7:00) проходит140 секунд. Предположим, что диагональное поле зрения видеорегистратора — 120° (это стандарт для большинства HD-видеорегистраторов). Тогда высота вспышки над горизонтом — ~30°. Скорость ударной волны грубо оценивается как Vзв∙Pф/Pa, где Pф — давление на фронте, Pa — атмосферное давление. Учитывая, что ударная волна не порушила каменных стенок и не сдвинула автомобили, можно предположить, что разность давления на фронте не превышала 10 кПа (это и так очень много — тонна на квадратный метр). А значит, можно считать, что на большей части своего пути ударная волна опережала звук не более, чем на 10%. Если за скорость звука на большей части пути принять 280 м/с (потому что температура вдоль большей части пути около -40°С – -50°С), то не будет большой ошибкой принять за скорость волны круглое число — 300 м/с.
Тогда высота взрыва метеорита получится 140∙300∙sin(30°) = 21 000 м.
Удаление объекта — 42 км. Угловая скорость перемещения 20° в секунду, откуда находим линейную скорость: 14,7 км/с. Таким образом, расчёт следует скорректировать. На данном ролике пиковая освещённость соответствует яркому солнечному дню — насыщения датчика не произошло — значит, не мене 70 тыс. но не более 100 тыс. люкс. Но зато расстояние до вспышки теперь мы знаем точно— 42 км. Спектр близок к солнечному, значит, на видимую область приходится 50% всей излучённой энергии. Продолжительность вспышки — 2 секунды.
Новая оценка энергии вспышки: 1,3∙1013 Дж. Предполагая, как и ранее, что в световое излучение уходит половина кинетической энергии, получаем энергию метеорита 2,6∙1013 Дж, откуда при скорости 14,7 км/с получаем массу в 240 тонн. Размер железного метеорита такой массы — 4 метра, каменного — 6 метров, ледяного — 8 метров.
Тротиловый эквивалент энергии взрыва: 6 килотонн.
UPDATE 2 Уточнение оценки массы и размеров метеорита с учётом новых данных и предположений![[profile]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%2017%2017'%3E%3C/svg%3E){kind=small}
v1adis1av прислал дополнительные ссылки: Вот статья в «Письмах ЖЭТФ», где утверждается, что в свет переходит 5%-10% начальной кинетической энергии. В статье в Nature приводится формула (фит по 15 событиям) для доли световой энергии: 
Я принимал, что в излучение переходит 25% кинетической энергии. Если уменьшить это значение до 5%-10%, то оценка массы метеорита возрастает в 2-5 раз и составит 400-1000 тонн.
Появились сообщения, что найдены фрагменты метеорита, химический состав которых указывает на то, что метеорит являлся каменным хондритом, таким образом, его плотность составляет от 2,2 до 3,2 г/см3. С учётом новой оценки массы размер метеорита будет составлять от 6 до 9 метров.
UPDATE 3 Критические замечания об оценке НАСА
НАСА утверждает, что получило свою оценку на основании энергии, перешедшей в ударную волну по результатам, полученных от своих инфразвуковых датчиков. Откуда может выделиться энергия, которая затем перейдёт в ударную волну? Очевидно, только из взаимодействия метеорита с воздухом (гипотезы ядерного взрыва самого метеорита рассматривать не будем за их неконструктивностью). Нетрудно подсчитать, какая масса воздуха может быть приведена в движение при торможении метеорита в атмосфере. Метеорит движется с гиперзвуковой скоростью и непосредственно взаимодействует только с тем воздухом, который находится внутри цилиндра, осью которого является траектория движения метеорита, а диаметром — диаметр метеорита. Для 15-метрового метеорита эта масса воздуха равна атмосферному давлению на высоте взрыва, умноженному на площадь сечения нашего цилиндра делённому на ускорение свободного падения и на синус угла наклона траектории к горизонту. Атмосферное давление на высоте 20 км 1/15 от нормального, то есть, над каждым квадратным сантиметром на высоте 20 км находится 1/15 кг воздуха. Площадь 15-метрового круга — 1.77∙106 кв. см, то есть, над кругом диаметром 15 метров на высоте 20 км находится 118 тонн воздуха. Итак, если такой метеорит, какой предлагает нам НАСА, падает отвесно, то до высоты 20 км он встречает на своём пути 118 тонн воздуха. Если наклон траектории составляет 10° к горизонту, то Метеорит тормозится уже об воздушную подушку массой 680 тонн. Но при массе метеорита 7000 тонн эта подушка уменьшит его скорость не более чем на 10%.
Какова же будет энергия ударной волны? Даже если весь воздух на пути метеорита разогнать до скорости последнего, ну, скажем, 20 км/с, затраченная энергия составит не более 1.4∙1014 Дж или, переводя в тротиловый эквивалент, 32 килотонны.
С другой стороны, если энергия взрыва составила, как утверждает специалист из НАСА, 500 килотонн ТНТ, и в ударную волну перешло всего 1% энергии взрыва, то для наблюдателя, находящегося в 42 километрах от центра взрыва, эта ударная волна должна ощущаться как взрыв ручной гранаты (заряд 25 г тротила) на расстоянии sqrt(0.025/(500.0e6*0.01)*42000.0 = 3 метра…
(этот аргумент некорректен).
Где-то что-то коллега из НАСА не учитывает, в его оценках элементарно не сходится энергетика. Либо референт, составлявший пресс-релиз, что-то недопонял.
UPDATE 4 Дополнительные соображения по поводу расхождения с НАСА
v1adis1av пишет: Энергия события вычисляется по эмпирической формуле dP(кПа) = 11.8*Е0.4 (кт)/ R1.2 (км), откалиброванной во времена воздушных ядерных испытаний. См. http://www.meteorites.com.au/odds&ends/Vitim%20Bolide%201.pdf
Вот, где, на мой взгляд, может быть нестыковка: ударная волна от ядерного взрыва на первых сотнях метрах своего распространения интенсивно диссипирует за счёт высвечивания на фронте. Светящаяся сфера, расширяющаяся при ядерном взрыве — это и есть фронт ударной волны. В случае с взрывом метеорита характерное время развития процесса измеряется не микросекундами, как при ядерном взрыве, а десятыми долями секунды, и, возможно, столь сильного высвечивания и диссипации энергии ударной волны не происходит. В этом случае приборы, откалиброванные по ядерным взрывам, дадут завышенную оценку энергии взрыва…
Но по сообщению v1adis1av, похоже, этот эффект сейчас учитывается. Вот пара интересных статей о оценке энергий болидов:
https://dl.dropbox.com/u/24173896/Articles/jastp-2006-68-1136.pdf
https://dl.dropbox.com/u/24173896/Articles/jastp-2012-80-208.pdf
UPDATE 5 Расчёт гиперзвукового торможения метеорита в атмосфере
На основании модели стандартной атмосферы и уравнения гиперзвукового сопротивления воздуха оценены зависимость высоты метеорита от времени после входа в атмосферу на высоте 100 км со скоростью 20 км/с под углом к горизонту 15° и зависимость скорости от высоты. Расчёты выполнены для железистого хондрита (плотность 3 г/см3) без учёта абляции и разрушения в атмосфере.
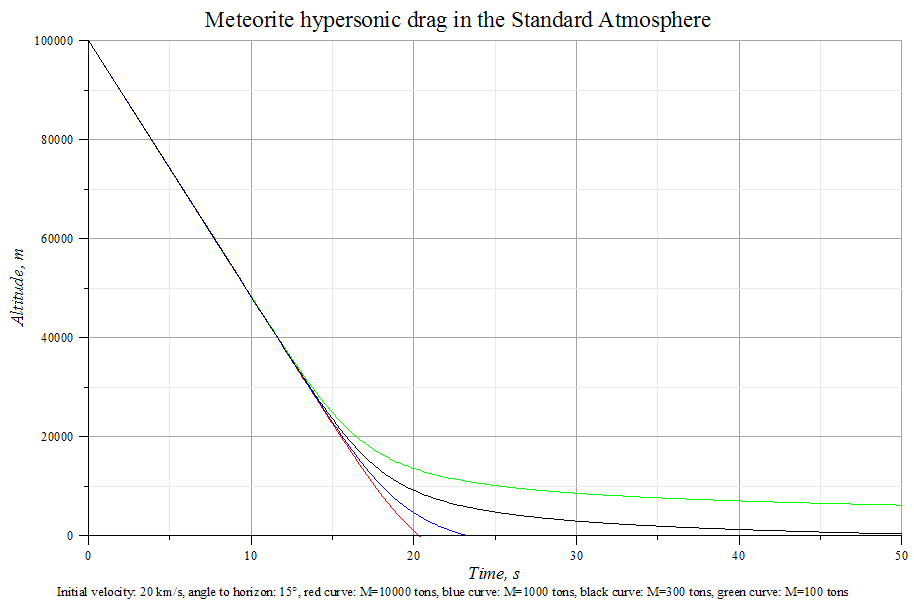
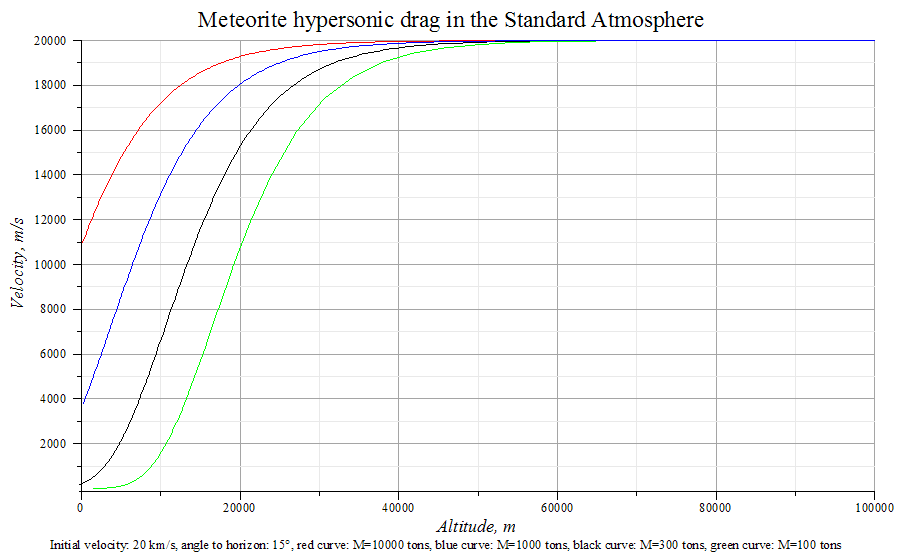
Кривая для метеорита массой 300 тонн лучше всего соответствует результатам, полученным при обработке записей видеорегистраторов, из которых следует, что в момент распада метеорит двигался на высоте 21 км со скоростью 15 км/с.
This entry was originally posted at http://apximhd.dreamwidth.org/12528.html. Please comment there using OpenID.
