Средняя скорость молекул
В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.
Средняя скорость движения молекул
Средняя скорость движения молекул называется также скоростью теплового движения молекул.
Формула средней относительной скорости молекул в физике представлена следующим выражением:
υotn=28kTπm0=2υ.
Средняя квадратичная скорость
Средняя квадратичная скорость движения молекул газа это следующая величина:
υkυ=1N∑i=1Nυi2
Формулу средней квадратичной скорости можно переписать так:
υkυ2=∫0∞υ2Fυdυ.
Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:
υkυ=3kTm0=3RTμ
Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:
p=13nm0υkυ,
где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.
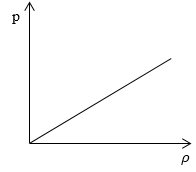
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).
Рисунок 1
Решение
Запишем выражение для средней скорости движения молекул газа следующим образом:
υ=8kTπm0
Из графика видно, что p~ρ или p=Cρ, где C – это некоторая константа.
m0=ρn, p=nkT=Cρ→kT=Cρn
Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:
υ=8kTπm0=8Cρπnnρ=8Cπ
Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.
Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?
Решение
Применим выражение для υkυ:
υkυ=3RTμ
Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:
pV=mμRT=NNART.
Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:
p=nNART→RT=pNAn
Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:
υkυ=3pNAμn
Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.
Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа
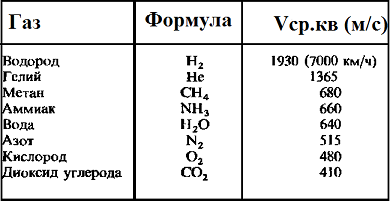
Таблица значений средней квадратичной скорости молекул некоторых газов
Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):
Где у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:
Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):
Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:
Но средняя кинетическая энергия, так же находится, как :
А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат,Число Авогадро на массу молекулы , получается Молярная масса то у нас и получится формула для средней квадратичной скорости молекулы газа:
А если расписать универсальную газовую постоянную, как , и за одно молярную массу
, то у нас получится?
В Формуле мы использовали :
— Средняя квадратичная скорость молекул
— Постоянная Больцмана
— Температура
— Масса одной молекулы
— Универсальная газовая постоянная
— Молярная масса
— Количество вещества
— Средняя кинетическая энергия молекул
— Число Авогадро
Значительная часть явлений молекулярной физики определяется скоростями молекул. Несмотря на это, нахождение скоростей молекул газа приобретает как теоретического, так и практического значения.
Виды скоростей молекул газа
Скорости газовых молекул в результате их хаотического движения отличаются как по величине, так и по направлению. Скорость данной молекулы газа в данный момент времени есть величина случайная. В молекулярно-кинетической теории газов пользуются понятиями средней (vv), средней квадратичной (vквv_{кв}) и наиболее вероятной (νHν_H) скоростей. Эти скорости задаются для равновесных состояний газа.
Средняя (или среднеарифметическая) скорость определяется уравнением
v=1n∑i=1nviv=frac{1}{n}sumlimits_{i=1}^{n}{{{v}_{i}}}
где viv_i – скорость ii-й молекулы;
nn –количество молекул.
Средняя квадратичная скорость определяется как:
vкв=v2=3kTm{{v}_{кв}}=sqrt{{{v}^{2}}}=sqrt{frac{3kT}{m}}
По этой формуле можно вычислить также скорость броуновских частиц. Конечно, при этом mm –масса броуновской частицы.
Выражению vквv_{кв} можно придать более удобный вид, умножив числитель и знаменатель под корнем на число Авогадро и учитывая, что kN=RkN = R и mN=МmN = М,
vкв=3RTM{{v}_{кв}}=sqrt{frac{3RT}{M}}
Среднюю квадратичную скорость называют еще тепловой. Значение vкв для газов достаточно велики. Так, для водорода при комнатной температуре vкв=1,9⋅103v_{кв} = 1,9 · 10^3 м/с, то есть около 2 км/с.
Тепловая скорость, как видно из уравнения, пропорциональна корню температуры и обратно пропорциональна корню массы. Это обстоятельство определяет, что тепловое движение– достаточно интенсивно для молекул, заметно для микроскопически малых частиц, которые осуществляют броуновское движение, и совершенно незаметно для тяжелых тел.
Экспериментальное определение скоростей газовых молекул
Большой интерес представляет непосредственное экспериментальное определение скоростей газовых молекул. Оно является прямым подтверждением многих результатов и положений молекулярно-кинетической теории. Впервые такое исследование провел А. Штерн в 1920 г. Источником атомов, скорость которых измерялась, в опыте Штерна был молекулярный пучок атомов серебра Ag. Схема установки приведены на рис. 1. На оси системы двух коаксиальных цилиндрических поверхностей натянуто платиновый провод, покрытый слоем серебра.
В других опытах использовали также висмут, кадмий, цезий.
Проволока разогревается электрическим током. Так, при температуре около 1300°С серебро с поверхности проволоки испаряется. Таким образом создавался линейный источник «Ag-лучей» и в камере цилиндров, воздух из которой предварительно откачивался при давлении 1,3 · 10-4 Па, образовывался одноатомный газ серебра. Часть атомов серебра через диафрагмы s1 и s2 проходила, образуя молекулярный пучок, к поверхности внешнего цилиндра, где оседала на прозрачной пластинке, создавая слой в виде узкой полосы.
Рис. 1
На первой стадии опыта Штерна установка находится в состоянии покоя. При достижении равновесного состояния (температура проволоки достигала определенного значения, которое определяли по её свечению) атомы серебра оседали у точки а1. На второй стадии опыта оба цилиндра приводились в достаточно быстрое вращение с частотой 41,7 с-1.
При этом атомы серебра, двигаясь в вакууме прямолинейно, оседали у точки b. Смещение полосы объясняется тем, что пока атомы серебра пролетают по инерции путь r, внешний цилиндр успевает вернуться на угол φ=ωtφ = ωt, то есть каждая точка внешнего цилиндра смещается на расстояние Δs=ωrtΔs = ωrt, где ωω –угловая скорость его вращения; tt –время, за который атомы серебра проходят путь r. Таким образом,
t=rv=Δsωrt=frac{r}{v}=frac{Delta s}{omega r}
где vv – скорость атомов серебра.
Отсюда
v=ωr2Δsv=frac{omega {{r}^{2}}}{Delta s}
Измеряя смещение полос атомов серебра ΔsΔs и угловую скорость вращения прибора, можно определить скорость атомов серебра. Она приблизительно описывалась выражением
(3,5kTm)12{{left( 3,5frac{kT}{m} right)}^{frac{1}{2}}}
что согласуется со средней скоростью молекул, которые определяются по формуле
v=8kTπmv=sqrt{frac{8kT}{pi m}}
Результаты опытов Штерна показали, что на самом деле картина структуры полосы сложнее.
Смещенная возле точки b полоса была не резко ограниченной, а размытой (рис. 2).
Рис. 2
Несмотря на то, что атомы серебра имеют разные скорости, более быстрым атомам должны соответствовать меньшие смещения, а тем более медленным – большие. Таким образом, результаты опыта Штерна вполне передают реальную картину теплового движения молекул.
Тест по теме «Скорость движения молекул»
Как определить скорость молекул газа? Помогите ответить!
Дима Федоренко
Ученик
(87),
закрыт
10 лет назад
Leonid
Высший разум
(388685)
11 лет назад
Строго – по распределению Максвелла.
Если нужна среднеквадратическая скорость – то по формуле Больцмана E = 3/2 kT. Это кинетическая энергия, приходящаяся в среднем на одну молекулу. По энергии и массе молекулы не штука найти скорость, соответствующую вот такой энергии.
Скорость молекул идеального газа
Средняя скорость молекул идеального газа (или средняя квадратичная скорость молекул) вычисляется по формулам, описанным ниже, и измеряется в м/с.
Формула скорости молекул газа
По формуле средней квадратичной скорости молекул вычисляется и скорость молекул идеального газа (v):

где R – универсальная газовая постоянная, равная 8,31, Дж/К•моль;
Т – температура, К;
М – молярная масса, кг/моль;
k – постоянная Больцмана, равная 1,38*10-23, Дж/К;
m – масса одной молекулы идеального газа, кг.
Известно, что молярная масса М равна произведению массы молекулы на число Авогадро 6,02*1023 (моль-1) , т.е. М = Nam.
Скорость молекул газа вычисляется в м/с.
Следовательно, скорость частичек газа зависит от температуры и их массы. Чем выше температура, тем быстрее движутся молекулы газа, а чем они тяжелее, тем медленнее их скорость.
Что такое идеальный газ
Идеальным считается настолько разряженный газ, что в нем можно пренебречь взаимодействием между молекулами. Иными словами в таком газе молекул настолько мало, что между ними почти не происходит столкновений и взаимного притяжения.
При небольшом давлении и не самой низкой температуре обычные газы близки к идеальному состоянию. Например, водород и кислород в обычных условиях можно считать идеальными газами.
Скорость молекул некоторых газов в обычных условиях приведены в таблице: