Как найти скорость моторной лодки по течению

Как найти собственную скорость лодки

Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение – самое главное в решении любого типа задач.

Инструкция

В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.

Первое, что необходимо выучить и знать “на зубок” – формулы. Запишите и запомните:

Vпо теч=Vс+Vтеч.

Vпр. теч.=Vс-Vтеч.

Vпр. теч=Vпо теч. – 2Vтеч.

Vпо теч.=Vпр. теч+2Vтеч.

Vтеч.=(Vпо теч. – Vпр. теч)/2

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, найдем:

Vтеч = (21,8 – 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Расстояние 24 24

Скорость Х-3 Х+3

время 24/ (Х-3) 24/ (Х+3)

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

20 мин=1/3 часа.

24/ (Х-3) – 24/ (Х+3) = 1/3

24*3(Х+3) – (24*3(Х-3)) – ((Х-3)(Х+3))=0

72Х+216-72Х+216-Х2+9=0

441-Х2=0

Х2=441

Х=21(км/ч) – собственная скорость парохода.

Ответ: 21 км/ч.

Обратите внимание

Скорость плота считается равной скорости водоема.

Источники:

• решение задач на течение

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Как найти собственную скорость лодки

• Как найти собственную скорость лодки
• Как решить задачу на скорость реки
• Как решать задачи на движение

Первое, что необходимо выучить и знать «на зубок» — формулы. Запишите и запомните:

Vпр. теч=Vпо теч. — 2Vтеч.

Vпо теч.=Vпр. теч+2Vтеч.

Vтеч.=(Vпо теч. — Vпр. теч)/2

Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.

На примере разберем, как находить собственную скорость и решать задачи такого типа.

Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:

Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.

За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.

Против теч. По течению

Расстояние 24 24

время 24/ (Х-3) 24/ (Х+3)

Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.

24/ (Х-3) – 24/ (Х+3) = 1/3

Х=21(км/ч) – собственная скорость парохода.

Источник

Какая скорость у моторной лодки: как правильно измерить и рассчитать?

Если лодка используется для водных прогулок, служебных нужд или для того, чтобы быстро добираться до места рыбалки, ключевым моментом при выборе моторки становится её скорость. В отношении того, какая скорость моторной лодки, точной цифры никто не скажет, потому что лодки отличаются друг от друга по конструкции, весу и т.п.. Поэтому мы расскажем вам, от чего зависит этот показатель, как он измеряется, приведём таблицы, в которых математические гении сделали некоторые расчеты и дадим формулы для самостоятельного расчёта.

Что влияет на скорость лодки?

Интересный факт! Spirit of Australia признан самым быстрым катером. Кен Варби спроектировал этот катер и показал на нем в 1978 году скорость 511 кмчас!

Факторы, от которых зависит скорость лодки:

1. Мощность двигателя. У каждого мотора свои характеристики, но мощность ограничивается конструктивными особенностями лодочного корпуса. Производители лодок указывают максимальную мощность и вес мотора, который допустимо ставить на конкретное судно. Превышать эти параметры крайне не рекомендуется, если вы не хотите пожертвовать своей безопасностью ради увеличения скорости. Кстати, от мощности установленного на вашу лодки мотора и от её веса зависит, нужно ли регистрировать судно в ГИМС или нет.
2. Гребной винт. Если правильно подобрать винт, это хорошо скажется на скорости. Во многих лодочных моторах установлены трёхлопастные винты. Винтовой диаметр зависит и от модели двигателя. Важная характеристика, которую нужно учитывать при выборе винта — шаг, измеряемый в миллиметрах и указывающий угол наклона лопастей.
3. Корпус лодки. Одна лодка может легко рассекать по воде, а другую нужно будет “заставлять” это делать. Многое зависит от корпусных обводов, материалов. Имеет значение и вес лодки. Например, если судно тяжело держит курс, на большую скорость рассчитывать не приходится. Стоит учитывать и загрузку лодки.
4. Погода. Если бушует ветер, и волны становятся всё активнее, скорость моторной лодки будет значительно ниже, чем на стоячей воде. Нельзя не учитывать направление течения реки или другого водоёма, которое тормозит или ускоряет судно.

Именно поэтому скорость движка не бывает одинаковой. Но, учитывая эти факторы, всегда можно рассчитывать на определённые показатели скорости. И, конечно, будьте внимательны, когда покупаете мотор. Смотрите на все параметры!

В нашем магазине вы найдёте отличные моторы с разными характеристиками. У нас есть движок, который даст нужную вам скорость!

Чем и как измеряется скорость лодки?

Скорость морских судов издавна принято измерять в узлах. Связано это с тем, что древние моряки узнавали скорость корабля с помощью устройства под названием “лаг” (название пошло от голландского слова log, означающего “расстояние”). Это было простое бревно, к которому привязывали верёвку. По её длине располагались завязанные узлы на равном друг от друга расстоянии. Второй конец такого каната закрепляли на борту корабля.

Чтобы измерять скорость, моряки бросали бревно в воду и считали, сколько узлов проходит через руки за конкретный промежуток времени. По числу таких узлов и определяли скорость корабля. Слово “узел” применяется до сих пор. В современном понимании под узлом понимается скорость (V), с которой судно проплывает одну морскую милю (1852 метра). Такой стандарт используется в разных странах как 1852 мчас или 1,852 кмчас. Значит, чтобы передать V в узлах в километрах, нужно умножить её на 1,852.

Приборы для измерения скорости

Конечно, сейчас бревна и веревки никто не используют. Современные судна требуют современных навигационных приборов! И такие есть. Разработаны вполне удобные спидометры, благодаря которым можно измерить скорость судна. Вот пара примеров устройств:

1. Манометрический спидометр. Аппарат со шкалой показывает V в км или милях в час. Есть модели, которые определяют скорость до 90 кмчас и выше. Выбирайте прибор, который подходит для вашей лодки. К примеру, зачем переплачивать за манометр со шкалой до 90 кмчас, если наибольшая скорость вашего судна 30 кмчас?
2. GPS-спидометр. Сигналы ему передают навигационные спутники. На плавсредстве крепится датчик рядом с самим прибором. Такое устройство отличается высокой точностью, но стоит дороже «обычных» моделей.

Интересный факт! Самой быстрой понтонной лодкой считается Brad Rowland’s South Bay 925CR, которая развила скорость 184 кмчас.

Есть такое понятие как «крейсерская скорость» моторки. Определение простое — это V при минимальных топливных затратах. Практически всегда это значение ниже максимального, зато расход топлива значительно меньше. Указывая характеристики моторок, часто указывают километры пути на 1 л топлива. В случае с парусными яхтами говорят о “средней скорости”, потому что парусник часто ходит галсами (галс — курс судна относительно ветра).

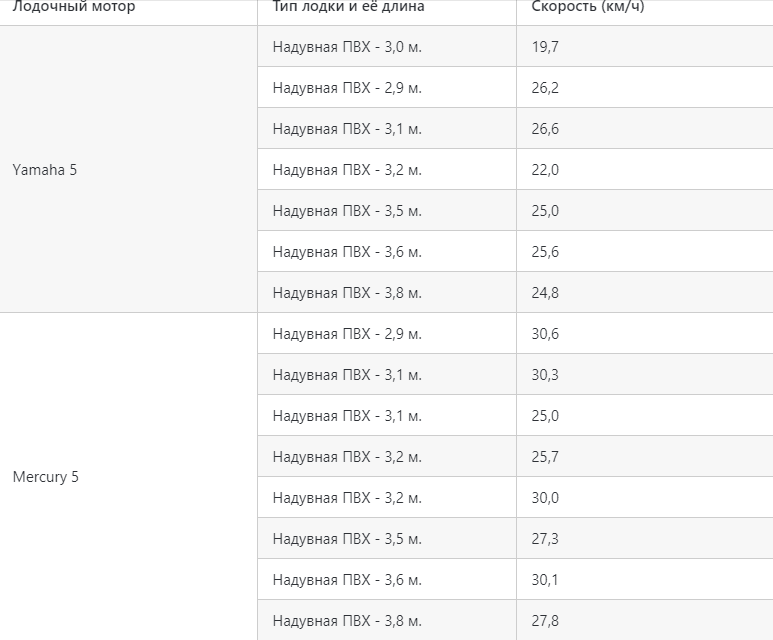
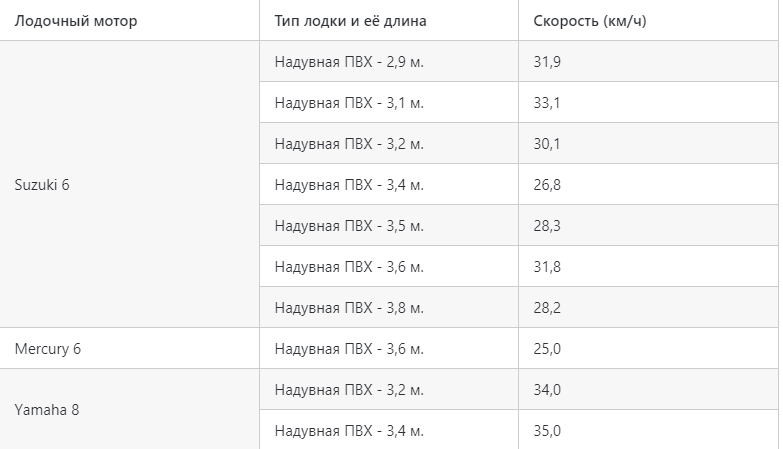
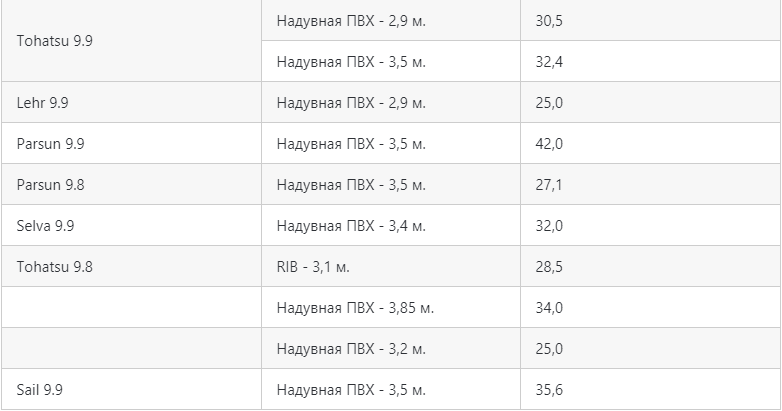
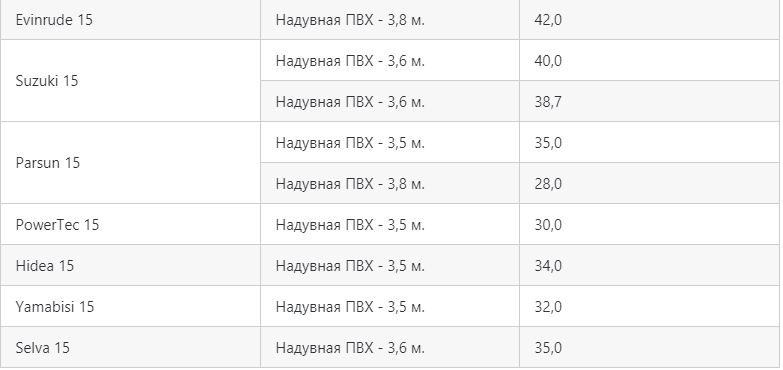
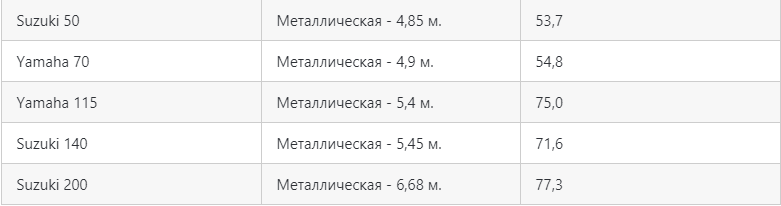
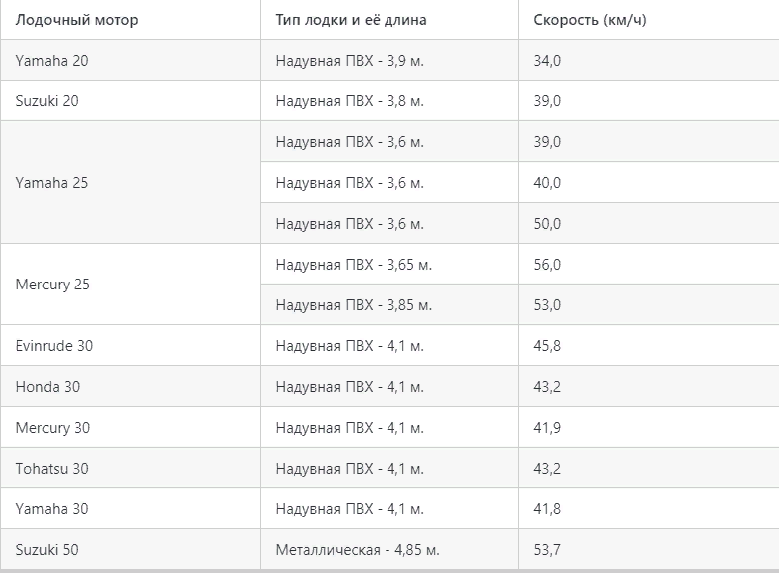
Полезные таблицы скоростей в зависимости от л.с

Некоторые любители математических расчётов провели исследования и показали, какая скорость моторной лодки в обычных условиях в зависимости от мощности. Мы нашли и привели эти расчеты ниже. Помните, что эти расчёты не претендуют на истину в последней инстанции, но помогают увидеть примерную картину.

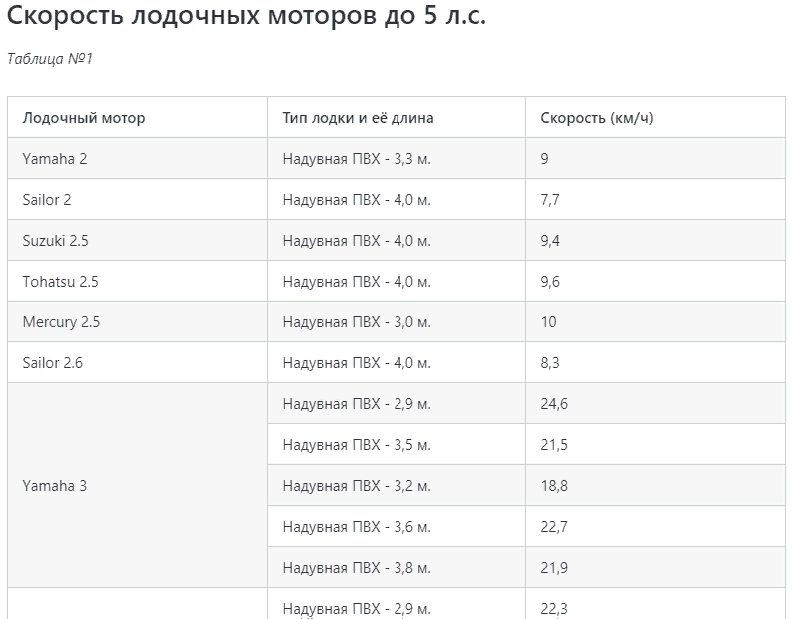
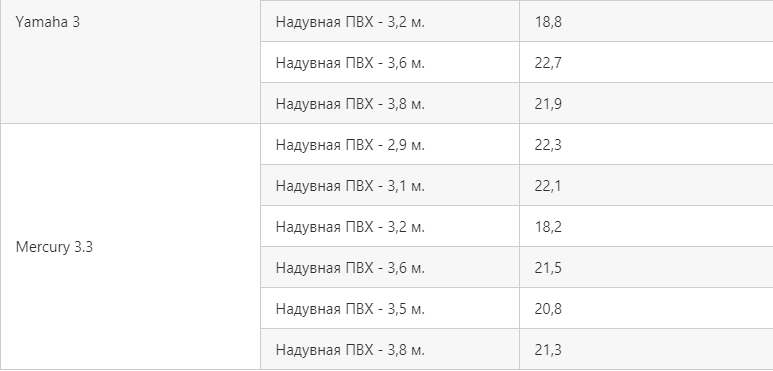
Средние и малопопулярные моторы свыше 5 и до 10 л.с:

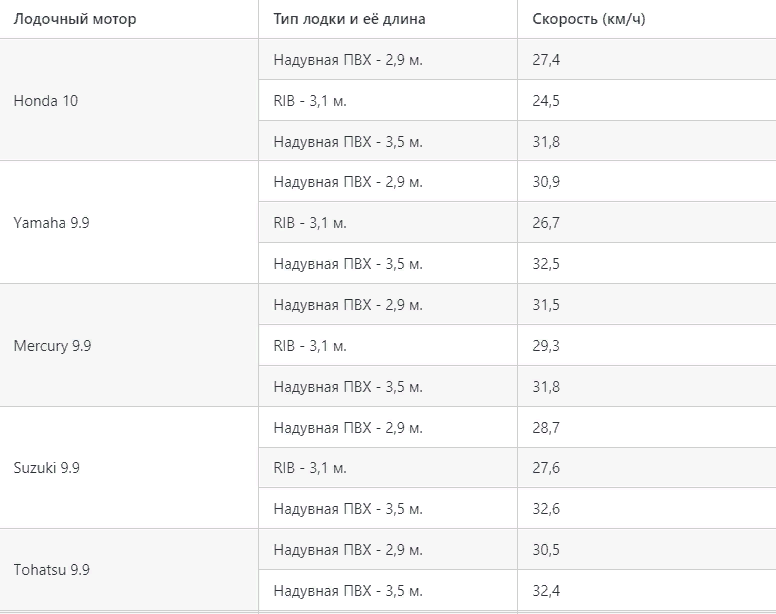
Скорость самых популярных лодочных моторов 9,9 л.с.:

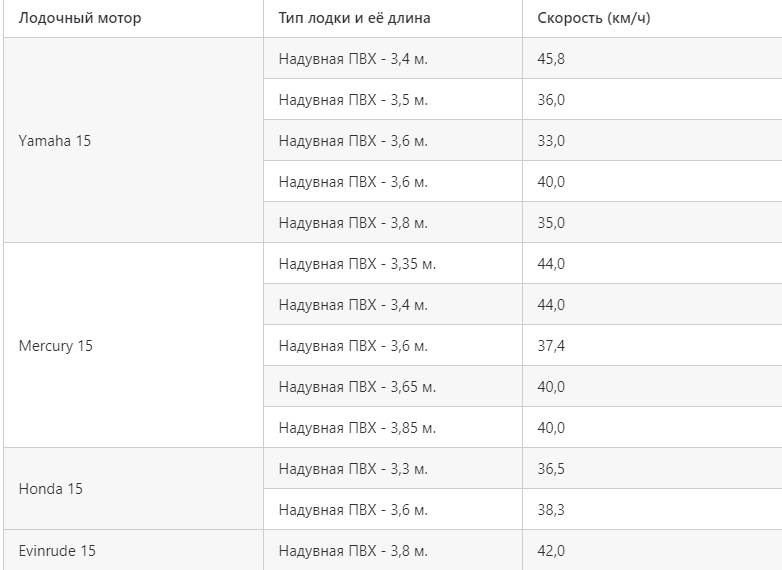
Лодочные моторы 15 л.с.:

Скорость движков, мощность которых превышает 15 л.с.:

Как рассчитать скорость своей моторной ПВХ лодки?

Находить V собственной лодки можно по простым формулам, как в школьных задачах.

Предположим, что V судна по течению воды составляет 30 кмчас, а против течения – 18 кмчас. Определяться со скоростью своей моторки можно с помощью такой формулы:

Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2.

Vтеч.= (30-18)/2 = 6 кмчас

Vс= (30+18) /2 = 24 кмчас

Ещё один легкий способ для самостоятельного расчёта предельной V судна основан на применении формулы, которая учитывает параметры мотора: V = NK/R, где R – сопротивление движению (есть в технической документации), K – коэффициент полезной деятельности винта (зависит от типа лодки), N – мощность работы двигателя (есть в технической документации). Для вычисления предела скорости судна нужно взять максимально допустимую мощность. Так можно высчитать предел максимальной скорости.

И, конечно, не забываем о старом добром способе измерения скорости в зависимости от времени и расстояния:

Теперь вы знаете, как понять, какая скорость моторной лодки. В нашем магазине вы можете купить не только отличные моторы, но и классные ПВХ-лодки.

Желаем вам хорошей и безопасной скорости и богатого улова!

Вопрос — ответ

Вопрос: Какая максимальная скорость у моторной лодки?

Имя: Камиль

Ответ: Всё зависит от нескольких факторов, главным образом, от мощности мотора. Производитель плавсредств указывает максимальную мощность и вес движка, который можно ставить на конкретную лодку. На скорость влияет ее корпус, гребной винт и погода.

Вопрос: Как и чем можно определить скорость своей лодки?

Имя: Рамиль

Ответ: Для этого используются спидометры, которые делятся на несколько видов. Наиболее точными считаются GPS-спидометры, которые связаны с навигационными спутниками. Могут помочь и готовые расчеты скорости для разных лодок и моторов.

Вопрос: С какой скоростью сейчас плывет моя моторная лодка?

Имя: Илья

Ответ: Кроме спидометра определить скорость своей лодки можно с помощью формул. Самая простая основана на использовании значений расстояния и времени (первое поделить на второе).

Источник

Как определить скорость движения лодки по течению реки

0

Пн-Пт 9:00-19:00
Сб-Вс 10:00-16:00

• Море моторов
• Как рассчитать по формулам скорость лодки?

Как рассчитать по формулам скорость лодки?

Собрали для Вас актуальные формулы, которые могут оказаться полезными каждому

8 июля 2020 1 132

✓ Формула 1

На примере разберем, как находить скорость лодки.

Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.

Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. — Vпр. теч)/2, найдем:

Vтеч = (21,8 — 17,2)/2=4,62=2,3 (км/ч)

Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)

Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).

✓ Формула 2

Самым простым методом самостоятельного расчета предельной скорости лодки считается использование формулы, учитывающей параметры двигателя.

Для этого используется формула вычисления двигателя V = NK/R, где искомый параметр V – скорость километров в час, R – сопротивление движению (его вы можете взять в технической документации своего катера), K – коэффициент полезной деятельности винта. Определяется он в зависимости от типа лодки. Так, для спортивного катера его значение — 160, для крупных винтов — 140, для средних и малых — 120 и 100 соответственно.

Параметр N – мощность работы двигателя катера. Эту информацию вы можете рассчитать самостоятельно или обратиться за помощью к технической документации. Для того, чтобы вычислить предел скорости катера, возьмите максимально допустимую мощность. Этот метод позволяет рассчитать предел максимальной скорости катера достаточно точно, однако не следует забывать про вероятную погрешность.

Возможно вам будет интересным

История производства подвесных лодочных моторов

С чего все началось? Рассказываем!

15 сентября 2020 401

Что такое виндсерфинг и зачем он нужен?

Подробнее рассказываем в нашей статье!

31 августа 2020 320

Этапы получения прав на маломерное судно

Получение любых прав на средства передвижения требуют определенных затрат, например: сбор необходимых документов, обучение, экзамены и многое другое. Рассказываем подробнее.

27 августа 2020 403

В чем плюсы бронирования лодок ПВХ?

Рассказываем особенности, читайте

20 августа 2020 361

5 мифов про лодки ПВХ

Таинственные лодки ПВХ и какие мифы их окружают?

17 августа 2020 327

Почему покупают детские велосипеды?

Хотите порадовать ребенка велосипедом? Отлично, наш ассортимент полон детских велосипедов!

10 августа 2020 315

Что нужно знать перед покупкой велосипеда?

Какие бывают велосипеды? Как выбрать? Читайте в статье

27 июля 2020 360

Как выбрать лодочный мотор?

Отвечаем на Вопросы наших покупателей

21 июля 2020 331

Что такое килеватость судна и на что влияет?

Читайте подробнее в статье!

14 июля 2020 912

Пункт выдачи заказов:
г. Санкт-Петербург, ул. Софийская д. 8к1 БЦ Крол

Пн-Сб 10:00-19:00
Вс 10:00-18:00

Остались вопросы?

Задайте их нам прямо сейчас!

© Море Моторов, 2021 | Все права защищены

Предложения, размещенные на сайте more-motorov.ru, не являются публичной офертой

Пожалуйста, введите Ваши данные, и менеджер свяжется с Вами в ближайшее время

Источник

Задачи на движение по реке

Задачи на движение по реке трудны для пятиклассников, а взрослые недоумевают: чего же там трудного? Бревно или плот плывут со скоростью течения реки V т., которая считается постоянной.

Скорость катера в стоячей воде V с. называют собственной скоростью катера. Скорость катера по течению реки V по теч. больше собственной скорости катера на скорость течения реки: V по теч. = V с. + V т.

Скорость катера против течения реки V пр теч. меньше собственной скорости катера на скорость течения реки: V пр. теч. = V с. – V т.

Эти соотношения полезно проиллюстрировать рисунком.

Скорость катера по течению больше его скорости против течения на две скорости течения.

Задача 1. Скорость катера в стоячей воде равна 15 км/ч, а скорость течения реки – 3 км/ч. Какова скорость катера по течению и против течения реки?

Решение.
1) 15 + 3 = 18 (км/ч) — скорость катера по течению реки,
2) 15 – 3 = 12 (км/ч) — скорость катера против течения реки.

Ответ. 18 км/ч и 12 км/ч.

Обратим внимание: скорость катера по течению реки — это сумма его собственной скорости и скорости течения реки, а скорость катера против течения реки— это разность его собственной скорости и скорости течения реки, поэтому скорость по течению реки больше скорости против течения на удвоенную скорость течения .

Задача 2. Скорость моторной лодки по течению реки равна 48 км/ч, а против течения — 42 км/ч. Какова скорость течения реки и собственная скорость моторной лодки?

Решение.
1) 48 – 42 = 6 (км/ч) — удвоенная скорость течения реки,
2) 6 : 2 = 3 (км/ч) — скорость течения реки,
3) 48 – 3 = 45 (км/ч) — собственная скорость.

Ответ. 3 км/ч и 45 км/ч.

Задачи для закрепления берём в учебнике «Математика» для 5 класса (Просвещение, С.М. Никольский и др.) или в книге для учителя «Обучение решению текстовых задач в 5-6 классах» (раздел Книги на сайте www.shevkin.ru ). Приведём только три задачи из учебника.

Если текст понравился, то ставим «палец вверх», подписываемся на канал. В комментариях оставляем возражения, предложения и пожелания.

Ваш наблюдатель Шевкин Александр Владимирович.

Источник

Данный материал представляет собой систему
задач по теме “Движение”.

Цель: помочь учащимся более полно овладеть
технологиями решения задач по данной теме.

Задачи на движение по воде.

Очень часто человеку приходится совершать
движения по воде: реке, озеру, морю.

Сначала он это делал сам, потом появились плоты,
лодки, парусные корабли. С развитием техники
пароходы, теплоходы, атомоходы пришли на помощь
человеку. И всегда его интересовали длина пути и
время, затраченное на его преодоление.

Представим себе, что на улице весна. Солнце
растопило снег. Появились лужицы и побежали
ручьи. Сделаем два бумажных кораблика и пустим
один из них в лужу, а второй – в ручей. Что же
произойдет с каждым из корабликов?

В луже кораблик будет стоять на месте, а в
ручейке – поплывет, так как вода в нем “бежит”
к более низкому месту и несет его с собой. То же
самое будет происходить с плотом или лодкой.

В озере они будут стоять на месте, а в реке –
плыть.

Рассмотрим первый вариант: лужа и озеро. Вода в
них не движется и называется стоячей.

Кораблик поплывет по луже только в том случае,
если мы его подтолкнем или если подует ветер. А
лодка начнет двигаться в озере при помощи весел
или если она оснащена мотором, то есть за счет
своей скорости. Такое движение называют движением
в стоячей воде.

Отличается ли оно от движения по дороге? Ответ:
нет. А это значит, что мы с вами знаем как
действовать в этом случае.

Задача 1. Скорость катера по озеру равна 16 км/ч.

Какой путь пройдет катер за 3 часа?

Ответ: 48 км.

Следует запомнить, что скорость катера в
стоячей воде называют собственной скоростью.

Задача 2. Моторная лодка за 4 часа проплыла по
озеру 60 км.

Найдите собственную скорость моторной лодки.

Ответ: 15 км/ч.

Задача 3. Сколько времени потребуется лодке,
собственная скорость которой

равна 28 км/ч, чтобы проплыть по озеру 84 км?

Ответ: 3 часа.

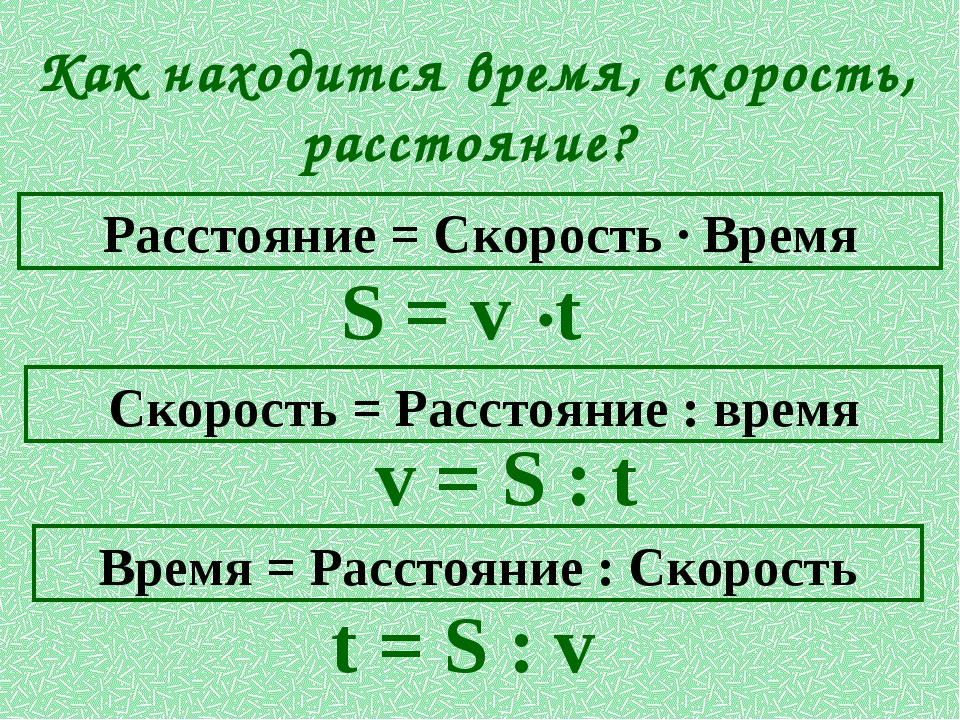
Итак, чтобы найти длину пройденного пути,
необходимо скорость умножить на время.

Чтобы найти скорость, необходимо длину пути
разделить на время.

Чтобы найти время, необходимо длину пути
разделить на скорость.

Чем же отличается движение по озеру от
движения по реке?

Вспомним бумажный кораблик в ручье. Он плыл,
потому что вода в нем движется.

Такое движение называют движением по течению.
А в обратную сторону –  движением против
течения.

Итак, вода в реке движется, а значит имеет свою
скорость. И называют ее скоростью течения реки.
( Как ее измерить?)

Задача 4. Скорость течения реки равна 2 км/ч. На
сколько километров река относит

любой предмет (щепку, плот, лодку) за 1час, за 4
часа?

Ответ: 2 км/ч, 8 км/ч.

Каждый из вас плавал в реке и помнит, что по
течению плыть гораздо легче, чем против течения.
Почему? Потому, что в одну сторону река
“помогает” плыть, а в другую – “мешает”.

Рис.1

Те же, кто не умеет плавать, могут представить
себе ситуацию, когда дует сильный ветер.
Рассмотрим два случая:

1) ветер дует в спину,

2) ветер дует в лицо.

И в том и в другом случае идти сложно. Ветер в
спину заставляет бежать, а значит, скорость
нашего движения увеличивается. Ветер в лицо
сбивает нас, притормаживает. Скорость при этом
уменьшается.

Остановимся на движении по течению реки. Мы уже
говорили о бумажном кораблике в весеннем ручье.
Вода понесет его вместе с собой. И лодка,
спущенная на воду, поплывет со скоростью течения.
Но если у нее есть собственная скорость, то она
поплывет еще быстрее.

Следовательно, чтобы найти скорость движения
по течению реки, необходимо сложить собственную
скорость лодки и скорость течения.

Задача 5. Собственная скорость катера равна 21
км/ч, а скорость течения реки 4 км/ч. Найдите
скорость катера по течению реки.

Ответ: 25км/ч.

Теперь представим себе, что лодка должна плыть
против течения реки. Без мотора или хотя бы весел,
течение отнесет ее в обратную сторону. Но, если
придать лодке собственную скорость ( завести
мотор или посадить гребца), течение будет
продолжать отталкивать ее назад и мешать
двигаться вперед со своей скоростью.

Поэтому, чтобы найти скорость лодки против
течения, необходимо из собственной скорости
вычесть скорость течения.

Задача 6. Скорость течения реки равна 3 км/ч, а
собственная скорость катера 17 км/ч.

Найдите скорость катера против течения.

Ответ: 14 км/ч.

Задача 7. Собственная скорость теплохода равна
47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите
скорость теплохода по течению и против течения.

Ответ: 51,9 км/ч; 42,5 км/ч.

Задача 8. Скорость моторной лодки по течению
равна12,4 км/ч. Найдите  собственную скорость
лодки, если скорость течения реки 2,8 км/ч.

Ответ: 9,6 км/ч.

Задача 9. Скорость катера против течения равна
10,6 км/ч. Найдите собственную скорость катера и
скорость по течению, если скорость течения реки
2,7 км/ч.

Ответ: 13,3 км/ч; 16 км/ч.

Связь между скоростью по течению и
скоростью против течения.

Введем следующие обозначения:

V_с. – собственная скорость,

V_теч. – скорость течения,

V _{по теч.} – скорость по течению,

V _пр.теч. – скорость против течения.

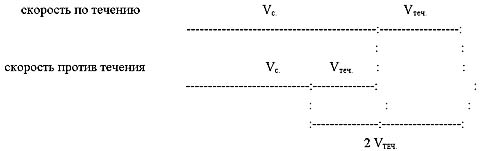
Тогда можно записать следующие формулы:

V _{no теч} ⁼ V_c + V_теч ;

V _{np. теч} ⁼ V_c – V _теч.;

Попытаемся изобразить это графически:

Рис. 2

Вывод: разность скоростей по течению
и против течения  равна удвоенной скорости
течения.

Vno теч — Vnp. теч = 2 Vтеч.

Vтеч = (V по теч – Vnp. теч ): 2

Задача.

1) Скорость катера против течения равна 23 км/ч, а
скорость течения 4 км/ч.

Найдите скорость катера по течению.

Ответ: 31 км/ч.

2) Скорость моторной лодки по течению реки равна
14 км/ч/ а скорость течения 3 км/ч. Найдите скорость
лодки против течения

Ответ: 8 км/ч.

Задача 10. Определите скорости и заполните
таблицу:

	V С.	Vтеч.	Vпо теч.	Vпр.теч.
1	12 км/ч	3 км/ч
2	23 км/ч		25 км/ч
3	24 км/ч			20 км/ч
4		4 км/ч	17 км/ч:
5		5 км/ч		18 км/ч
6			42 км/ч	34 км/ч

* – при решении п.6 смотри рис.2.

Ответ: 1) 15 и 9; 2) 2 и 21; 3) 4 и 28; 4) 13 и 9; 5)23 и 28; 6) 38 и 4.

Задачи на движение по реке

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.

Здравствуйте, дорогие читатели, подписчики и гости канала. Продолжаем разбор текстовых задач из ОГЭ 2021 года, входящие в 21 задание. Рассмотрим решение задач на движение по воде. В задачах за неизвестное (Х) будем брать то, что нужно найти.

Задача №1

Пусть Х – собственная скорость баржи. Если баржа плывет по течению реки, то ее собственная скорость увеличивается на скорость реки, и наоборот. Все данные из задачи перенесем в таблицу.

Так как весь путь по течению реки и против течения составил 5 часов, то составим уравнение:

Решим уравнение:

Задача №2

Пусть Х – скорость лодки в неподвижной воде. Тогда по течению реки будет Х+5, против течения реки Х-5.

Важно! Скорость течения реки равна 3 км/ч, с этой же скорость плывет плот, так как у плота нет своей скорости. Зная скорость плота и расстояние, которое плыл плот. Время, которое плыл плот равно: 33:3=11 часов.

Моторная лодка вышла вслед за плотом через один час, значит она плыла 10 часов. Составим уравнение:

Решим уравнение:

Задача №3

Пусть Х – скорость лодки в неподвижной воде. Тогда скорость лодки по течению будет равна Х+4, против течения Х-4. Внесем все данные в таблицу и найдем время движения лодки по течению и против течения реки.

Время движения против течения реки больше чем время движения по течению на 2 часа. Составим уравнение:

Решим уравнение, найдем скорость лодки в неподвижной воде:

Задача №4

Пусть Х – скорость течения реки. Тогда скорость теплохода по течению реки будет 25+х, против течения – 25-х.

Найдем, сколько времени был теплоход в пути. Теплоход вернулся в пункт отправления через 32 часа, а стоял в пункте назначения 21 час, значит в пути по воде в обе стороны теплоход плыл 32-21=11 часов.

Составим уравнение:

Решим уравнение и найдем скорость течения реки:

Спасибо, что дочитали. Вы меня очень поддержите, если поставите класс и подпишитесь на мой блог.

Путеводитель по каналу здесь