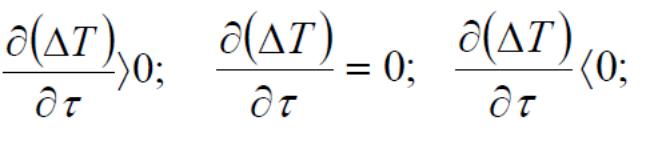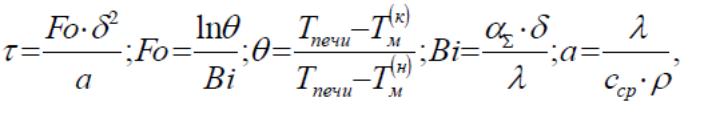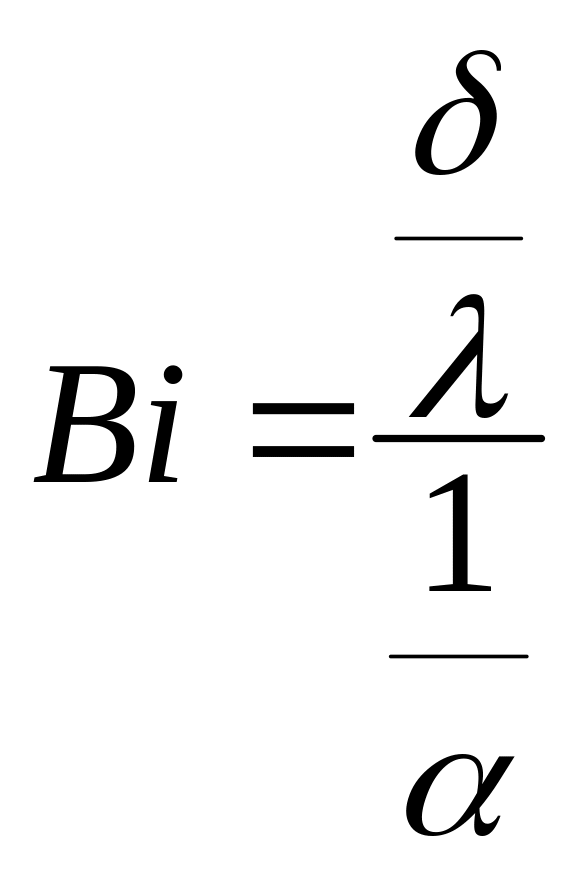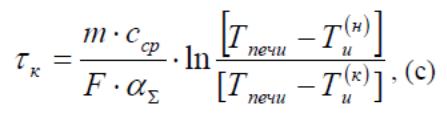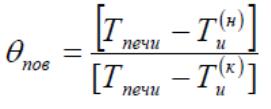График плавления и отвердевания тела показывает нам
все этапы процесса. Из него мы можем извлечь информацию о температуре плавления
тела, например, о том, как долго это тело потребовалось нагревать, чтобы
достичь той или иной температуры. Для понимания того, как строятся подобные
графики, рассмотрим некоторые примеры.
На рисунке представлен график плавления и отвердевания
железа.
В начальный момент времени, температура была равна
1200 оС, и пока она не достигла 1539 оС, плавление не
началось. Молекулы сохраняли свой порядок, что характерно для твёрдого тела. По
достижении температуры плавления, порядок нарушается, поскольку тело переходит
в жидкое состояние. Его температура какое-то время остаётся постоянной, о чем
свидетельствует горизонтальный участок графика. После того, как железо
полностью расплавилось, температура снова начала увеличиваться. Порядок
полностью нарушился, поскольку этот участок графика соответствует периоду,
когда железо было полностью жидким. Достигнув отметки 1880 оС,
железо перестали нагревать, и температура начала падать. Достигнув температуры
кристаллизации, железо начало твердеть. Это заняло какое-то время, в течение
которого температура вновь не менялась, начал восстанавливаться порядок. После
этого, температура стала ниже температуры отвердевания, и железо вновь стало
полностью твёрдым, а порядок молекул восстановился. Этому соответствует
последний участок графика.
Упаржнения.
1. Построить график
плавления олова. Температура плавления составляет 232 оС, а
начальная температура 200 оС. За 5 мин олово достигнет температуры
плавления, и ещё 5 мин будет плавиться. 2,5 мин занимает нагревание олова от
температуры плавления до 250 оС, и столько же займет охлаждение до
232 оС.
Итак, возьмём 20 оС за одну клетку по
вертикали и 2,5 мин за одну клетку по горизонтали. Тогда первая точка будет
иметь координаты 0 минут и 200 градусов, а вторая — 5 минут и 232 градуса.
Соединим эти две точки. В этой точке начинается плавление длительностью 5
минут. Температура не меняется, поэтому координаты третьей точки будет 10 минут
и 232 градуса. После этого, олово нагревается до 250 градусов за 2,5 минуты,
поэтому координаты четвёртой точки будут 12,5 минут и 250 градусов. Это точка
является пиком графика, поскольку в этот момент олово достигло наивысшей
температуры. Дальше график симметричен, поэтому абсолютно аналогичным способом
достраиваем и вторую часть графика.
Для построения этого графика мы использовали некую
начальную информацию о теле. Значит, из готового графика можно извлечь
информацию.
2. На рисунке представлен график
плавления и отвердевания для какого-то вещества.
И нам надо найти ответы на вопросы:
— Какой самой высокой температуры достигло вещество?
Итак, смотрим на график. Вертикальная ось
соответствует температуре, следовательно, наивысшая температура соответствует
пику графика. Это 1250 оС.
— Какова температура плавления данного вещества?
Температуре плавления соответствуют горизонтальные
участки графика, поскольку температура остаётся неизменной во время плавления
или кристаллизации. На графике видно, что горизонтальные участки соответствуют
температуре 1000 оС, поэтому, это и есть температура плавления.
— Сколько времени заняло плавление, и сколько времени
заняла кристаллизация?
На графике мы видим, что по горизонтальной оси,
соответствующей времени между отметкой 0 и отметкой 40 — две клетки. Длина
горизонтальных отрезков тоже составляет две клетки. Поэтому, и плавление, и
кристаллизация заняли по 40 минут.
— Какова скорость нагревания данного вещества в
твердом состоянии, и какова скорость нагревания в жидком состоянии?
По вертикальной оси расстояние между отметкой 1000 и
отметкой 1250 — одна клетка. Следовательно, расстояние в две клетки
соответствует пятистам градусам. Тогда, в начальный момент времени, температура
составляла 500 градусов. Мы видим на графике, что температура достигла
температуры плавления за 40 минут. Поэтому, скорость нагревания в твердом
состоянии равна 500 оС за 40 минут, т.е. 12,5 оС/мин.
На графике видно, что вещество в жидком состоянии
нагрелось от 1000 оС до 1250 оС. По горизонтальной оси,
длина этого процесса соответствует одной клетке, а, значит, двадцати минутам,
т.к. 40 минут — это две клетки. Значит, скорость нагревания в жидком состоянии
равна 250 оС за 20 минут, т.е. 12,5 оС/мин.
Следует помнить о том, что нагревание вещества в
твердом состоянии на самом деле может происходить не с той же скоростью, что и
нагревание вещества в жидком состоянии. Да и зависимость скорости нагревания
или остывания от температуры может быть нелинейной. Несмотря на это, даже из
такого графика можно извлечь, некоторую информацию.
Данный график предполагает достаточно сложные математические
операции для подробного анализа, с которыми мы познакомимся намного позже.
Однако, у нас достаточно знаний, чтобы ответить на следующие вопросы:
— Какая максимальная температура была достигнута
данным веществом?
Опять же, обращаемся к самой высокой точке. Она
соответствует 450 оС.
Держалась ли в какой-нибудь момент времени постоянная
температура свыше 315 оС?
Постоянной температуре будет соответствовать
горизонтальный участок графика. На данном графике, такой участок только один.
Исходя из того, что отметка 450 оС находится на расстоянии 3 клетки
от нулевой отметки по оси температуры, одна клетка соответствует 150 оС,
а 2 клетки — 300 оС. Мы видим, что наш горизонтальный участок
находится ниже отметки оС градусов, следовательно, температура выше
315 оС не держалась.
— Определите, нагревалось тело или остывало в первые
12 минут?
Одна клетка по горизонтальной оси соответствует 20
минутам. Мы видим, что на промежутке, более длительном, чем 12 минут,
температура увеличивалась с течением времени. Следовательно, тело нагревалось.
Определите среднюю скорость нагревания в период с 40
до 100 минут.
Итак, отмечаем на графике интервал от 40 до 100 минут.
Мы видим, что в этот период температура менялась по какому-то сложному закону.
Однако, мы знаем, что бы ни происходило в этот период, температура возросла от
150 оС до 450 оС за 60 минут. Поэтому, в среднем, тело
нагревалось со скоростью 300 оС в час или 5 оС в минуту.
При построении графиков помните, что очень важно
соблюдать масштабирование, т.е. равные интервалы, относящиеся к одной и той же
величине, обозначать равным количеством клеток.
Уравнение нагревания
Хотя электрическая машина имеет сложное устройство, в основу анализа процесса ее нагревания может быть положена теория нагревания идеального однородного твердого тела, под которым здесь понимается тело, обладающее равномерным рассеянием тепла со всей поверхности и бесконечно большой теплопроводностью, вследствие чего все точки тела имеют одинаковую температуру. Составим дифференциальное уравнение нагревания такого тела, для чего рассмотрим его тепловой баланс.
Пусть в единицу времени в теле выделяется количество теплоты Q. Тогда за бесконечно малый промежуток времени выделяемое количество теплоты будет равно Q × dt. Эта теплота частично аккумулируется в теле при повышении температуры и частично отдается во внешнюю среду.
Если за время dt температура тела повысилась на dΘ, то количество аккумулируемой за это время теплоты равно G × c × dΘ, где G – масса тела и c – его удельная теплоемкость.
Пусть в рассматриваемом бесконечно малом интервале времени превышение температуры тела над температурой окружающей среды равно Θ. Тогда количество теплоты, отдаваемое в окружающее пространство за время dt вследствие лучеиспускания, конвекции и теплопроводности, будет равно S × λ × Θ × dt, где S – площадь тела и λ – коэффициент теплоотдачи с поверхности.
На основе закона сохранения энергии
| Q × dt = G × c × dΘ + S × λ × Θ × dt . | (1) |
Прежде чем приступить к решению уравнения нагревания (1), несколько преобразуем его.
Установившееся превышение температуры и постоянная времени нагревания
После истечения достаточно длительного времени (теоретически при t = ∞) температура тела достигает установившегося значения. Тогда dΘ = 0 и Θ = Θ∞. Подставив эти значения в выражение (1), получим
Q ×dt = S × λ × Θ∞ × dt ,
откуда
| (2) |
Установившееся превышение температуры Θ∞ тем больше, чем больше выделяется тепла и чем хуже условия ее отдачи, то есть чем меньше S × λ.
Разделим обе части выражения (1) на S × λ, используем равенство (2) и обозначим
| (3) |
Тогда вместо (1) получим
| Θ∞ × dt = T × dΘ + Θ × dt. | (4) |
Размерность всех членов (4) должна быть одинакова – температура, умноженная на время. Поэтому T имеет разность времени, что можно установить также по формуле (3). Величина T называется постоянной времени нагревания тела; согласно формуле (3), она тем больше, чем больше теплоемкость тела G × c и чем меньше интенсивность отдачи тепла, то есть меньше S × λ.
Если определить из равенства (2) S × λ и подставить в (3), то получим еще одно выражение для T:
| (5) |
Числитель этого выражения равен количеству теплоты, накопленной в теле при достижении Θ = Θ∞.
Следовательно, в соответствии с выражением (5) постоянная времени нагревания T равна времени, в течение которого температура достигла бы установившегося значения Θ∞, если бы отсутствовала передача тепла в окружающую среду и все выделяемое тепло накапливалось в теле.
Решение уравнения нагревания
В уравнении (4) можно разделить переменные и привести его к виду
| (6) |
При интегрировании уравнения (6) получим
| t / T = – ln (Θ∞ – Θ) + C . | (7) |
Постоянная C определяется из начального условия: при t = 0 тело в общем случае имеет некоторое превышение температуры Θ = Θ0. Подставив указанные значения t и Θ в (7), найдем, что
C = ln (Θ∞ – Θ0) .
Подставим это значение C в (7) и переменим знаки. Тогда
откуда окончательно для Θ = f(t) находим
| Θ = Θ∞ × (1 – e–t/T) + Θ0 × e–t/T . | (8) |
Случай нагревания при Θ0 = 0
В этом случае вместо выражения (8) имеем
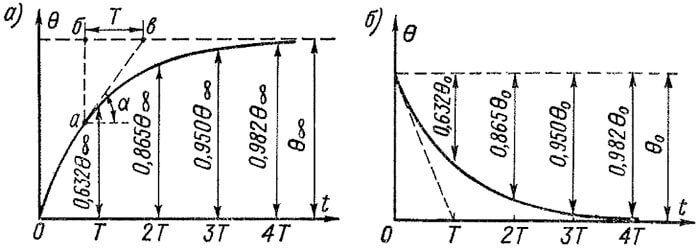
чему соответствует экспоненциальная кривая нагревания, изображенная на рисунке 1, а. При малых t, когда и Θ мало, теплопередача в окружающее пространство также мала, большая часть тепла накапливается в теле и температура его растет быстро, как это видно из рисунка 1, а. Затем с ростом Θ теплоотдача увеличивается и рост температуры тела замедляется. При t = ∞, согласно равенству (9), Θ = Θ∞.
На рисунке 1, а указаны значения Θ, достигаемые через интервалы времени T, 2T, 3T и 4T. Из этого рисунка видно, что тело достигает практически установившегося превышения температуры через интервал времени t = 4T.
Охлаждение тела
Если тело имеет некоторое начальное превышение температуры Θ ≠ 0, но Q = 0 и, следовательно, в соответствии с выражением (2) Θ∞ = 0, то происходит охлаждение тела от Θ = Θ0 до Θ = Θ∞ = 0.
Подставив в (8) Θ∞ = 0, получим уравнение охлаждения тела
Экспоненциальная кривая охлаждения тела согласно уравнению (10) представлена на рисунке 1, б. Сначала, когда Θ и соответственно также теплоотдача велики, охлаждение идет быстро, а по мере уменьшения Θ охлаждение замедляется. При t = ∞ будет Θ = 0.
Рисунок 1. Кривые нагревания (а) и охлаждения (б) идеального однородного твердого тела
Общий случай нагревания тела
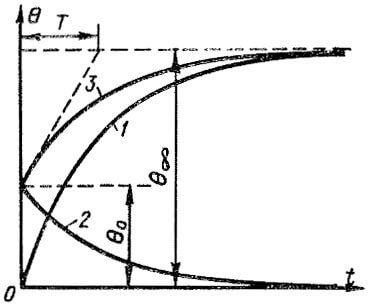 |
| Рисунок 2. Общий случай нагревания идеального однородного твердого тела |
Общий случай нагревания тела, описываемый уравнением (8), на основании формул (9) и (10) можно рассматривать как наложение двух режимов: 1) нагревания тела от начального превышения температуры Θ = 0 до Θ = Θ∞ и 2) охлаждения тела от Θ = Θ0 до Θ = 0. На рисунке 2 кривая 3 представляет собой кривую нагревания, построенную по уравнению (8). Эту кривую можно получить путем сложения ординат кривых 1 и 2, соответствующих уравнениям (9) и (10).
Графический способ определения T
Найдем подкасательную бв (рисунок 1, а), отсекаемую на асимптоте Θ = Θ∞ касательной к кривой Θ = f (t). Из рисунка 1, а следует, что
| (11) |
где α – угол наклона касательной к кривой Θ = f(t).
Как известно,
Но, согласно выражению (6),
| (12) |
Подставив tg α из (12) в (11), получим
бв = T .
Таким образом, подкасательная к любой точке кривой нагревания или охлаждения равна постоянной времени нагревания T. Этим свойством кривых Θ = f(t) можно воспользоваться для графического определения T, если имеется кривая Θ = f(t), снятая, например, опытным путем. На рисунке 1, б и 2 показан способ определения T при построении касательной к начальной кривой.
Заключительные замечания
Выше была изложена теория нагревания идеального однородного твердого тела. В действительности электрическая машина не представляет собой такого тела, так как она состоит из разных частей, обладающих конечной теплопроводностью, причем теплопроводность электрической изоляции достаточно мала. Поэтому отдельные части машины (обмотка, сердечники и другие) имеют различные температуры. В связи с этим более правильно было бы рассматривать электрическую машину как совокупность нескольких однородных тел, между которыми существует теплообмен. В действительных условиях величина T также не вполне постоянна, так как коэффициенты теплоотдачи зависят в определенной мере от температуры. Кроме того, воздух или другой охлаждающий агент при протекании по вентиляционным каналам нагревается, и поэтому температура охлаждающей среды для различных участков охлаждаемой поверхности имеет различные значения.
Таким образом, кривые нагревания и охлаждения не являются, строго говоря, экспоненциальными. Однако в большинстве практических случаев мы не делаем существенных ошибок, считая их экспоненциальными, то есть применяя изложенную выше теорию нагревания идеального однородного тела.
Источник: Вольдек А. И., “Электрические машины. Учебник для технических учебных заведений” – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
При любом
технологическом процессе тепловой
обработки основными
параметрами нагрева
материала являются:
– конечная
температура нагрева;
– температурная
скорость нагрева
до конечной температуры;
– время
выдержки при конечных температурах
нагрева;
– количество
теплоты
для обеспечения заданного нагрева;
– температурная
скорость
охлаждения
после выдержки до заданной температуры.
Конечная
температура нагрева
Любая тепловая
обработка материала связана с его
нагревом от начальной температуры (Тн)
до заданной
конечной температуры (Тк).
Значение конечной температуры зависит,
главным образом, от цели (технологической
задачи) процесса нагрева материала
(сушки, нагрева, плавки и т.п.).
При термообработке
конечная температура нагрева назначается
в соответствии с видом термообработки
по значениям критических
температур изменения
структуры
или свойств сплава в отливке (они
характерны только для этого типа сплава).
Например,
для
осуществления полного отжига
стальных отливок необходимо их нагревать
до конечной температуры, равной на
30-50К выше критической точки окончания
образования аустенита (точки АС3),
что составляет 1223-1323К (950-10500С).
При плавке конечная
температура
нагрева
(перегрева) определяется прежде всего
температурой
плавления сплава,
а затем уже характером внепечной
обработки жидкого сплава, условиями
его заливки в литейную форму и
конструктивной сложностью изготовляемой
отливки (габаритными размерами, массой,
толщиной стенки
и т.д.). Например,
температура выпуска ЧПГ из печей, в
зависимости от вида литья, находится в
пределах 1583-1653К (1310-13800С),
а температура выпуска нелегированных
сталей из печей – 1793-1823К (1520-15500С).
При
сушке материалов
конечная температура
нагрева
определяется критическими
температурами
необратимых физико-химических процессов,
происходящих в материале или в каких-то
его компонентах. Например,
конечная температура сушки формовочного
песка находится в пределах 773-873К
(500-6000),
стержней и форм на органических водных
связующих – в пределах 423-453К (150-1800),
а на глинистых связующих – в пределах
723-773К (450-5000).
Температурная
скорость нагрева
Скорость нагрева
материала, или температурная скорость
нагрева
в основном
определяется следующими тремя факторами:
– поставленной
технологической задачей
нагрева
(сушка, термообработка, плавка и т.п.);
– теплофизическими
характеристиками
материала (теплоемкостью, теплопроводностью,
температуропроводностью и т.п.);
– размерными
и количественными характеристиками
материала
или изделия (массой, габаритными
размерами, толщиной стенок и т.п.).
Часто скорость
нагрева является основополагающим
параметром тепловой обработки материала.
Поэтому необходимо более подробно
рассмотреть вопрос выбора данного
параметра.
Если исходить из
экономических
соображений
выбора
температурной скорости нагрева материала,
то ее значение
должно быть максимально возможным.
Т.к. в этом случае сокращается время
тепловой обработки и повышается тепловое
к.п.д. Именно такой нагрев применяется
в основном при плавке шихты в печах,
т.к. скорость нагрева и плавления шихты
не оказывает значительного влияния на
физико-химические свойства конечного
изделия – отливки.
Для
обеспечения максимально допустимой
скорости нагрева
необходимо создать в печи такие тепловые
условия, при которых возникал бы
максимально возможный тепловой поток
к поверхности обрабатываемого материала.
Такие тепловые условия в печи могут
возникать:
– при создании
максимально
возможной разности температур
(ΔТ) между
теплоносителем и нагреваемым материалом
(т.е. создании максимального градиента
температур);
– при создании
интенсивного
движения теплоносителя
(печных газов) в рабочем пространстве
топливных печей, что увеличивает тепловой
поток к нагреваемому материалу за счет
конвективной составляющей теплообмена.
Однако,
во многих случаях, очень высокая скорость
нагрева может вызвать опасность перегрева
поверхности материала (особенно
массивного) и даже его разрушения под
действием температурных напряжений.
Это говорит о том, что скорость нагрева
материала в каждом конкретном случае
должна иметь вполне определенное
значение.
Критерием оценки
правильного
выбора
значения температурной скорости нагрева
может служить температурная
равномерность нагрева
материала. Показателем
температурной равномерности нагрева
является скорость
изменения разности температур
поверхности и центральной части
нагреваемого материала (ΔТ
= Тпов. – Тц) во
времени:
(1.1)
В случае когда ΔТ
не изменяется
во времени (ΔТ-
const) нагрев
считается равномерным.
Равномерность
или неравномерность нагрева
всегда связана с совместным решением
внутренней и внешней задач нагрева.
Решение
внешней задачи нагрева
обеспечивается
определенным количеством
теплового потока
(Qпов)
от
теплоносителя к поверхности материала.
Например,
если принять, что теплоотдача в основном
осуществляется по закону Ньютона-Рихмана,
то тогда значение
внешнего теплового потока
можно определить по следующему уравнению:
(1.2)
где
– суммарный
коэффициент теплоотдачи (
);
F –
тепловопринимающая поверхность материала
(м2);
ТТ;
Тпов.
– температуры
теплоносителя и поверхности материала
соответственно (К).
Решение
внутренней задачи нагрева
обеспечивается
определенным тепловым потоком от
поверхности внутрь материала.
Решение этой задачи зависит
от свойств материала
(геометрических, теплофизических и
т.п.).
При этом внутренний
тепловой поток к центру изделий можно
определить по следующей формуле:
(1.3)
где λ
– коэффициент
теплопроводности материала
;
δ –
расчетная толщина материала (м);
Тпов.;
Тц
– температуры
поверхности и центра материала (К);
F –
тепловоспринимающая поверхность
материала (м2).
Здесь следует
отметить, что при
нагреве жидких материалов решение
внутренней задачи ускоряется за счет
перемешивания,
т.е. внутренний теплоперенос начинает
осуществляться не только за счет
теплопроводности, но и за счет конвекции.
Равномерность
нагрева материала будет соблюдаться
только при
равенстве внешнего и внутреннего
тепловых потоков:
Qпов.
= Qц.
(1.4)
В случае, когда
Qпов.
> Qц
, нагрев
внешней поверхности
материала будет осуществляться быстрее,
чем его центральная часть, т.е.:
(1.5)
Чем выше
скорость роста
ΔТ, тем
выше
перегрев поверхности материала,
тем вероятнее
возникновение недопустимых термических
напряжений.
Поэтому скорость
нагрева должна быть ограничена
каким-то предельно допустимым значением.
Во многих случаях,
особенно при термообработке отливок,
скорость
нагрева
определяется скоростью
заданного изменения структуры
сплава, скоростью диффузии и т.п. Поэтому
скорость нагрева, особенно при
термообработке, назначается специальным
температурным графиком нагрева материала.
В качестве примера,
на рис. 1.1 представлен температурный
график нагрева отливок различной толщины
из стали марки 40ГЛ для проведения
специального вида термообработки –
отжига.
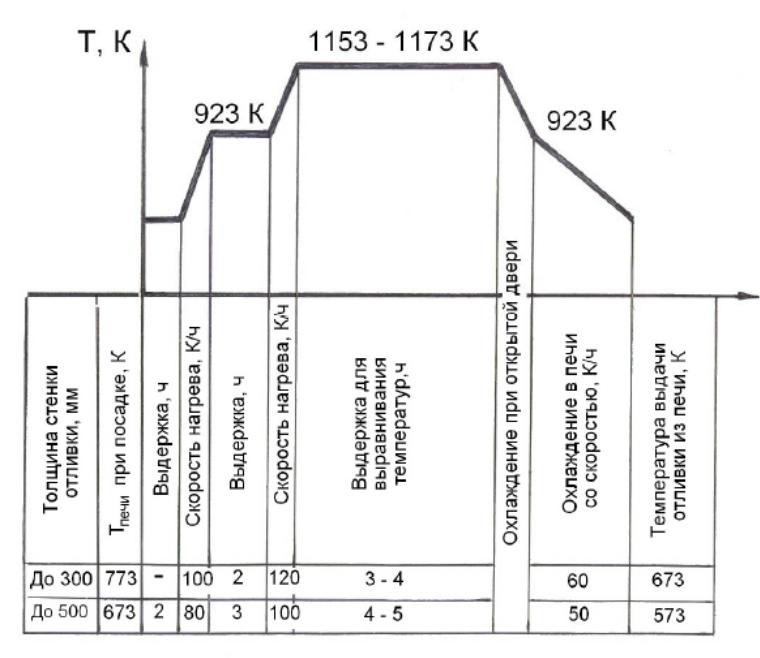
Рис.
1.1. Температурный график нагрева отливок
из стали марки 40ГЛ для термообработки
Время нагрева
и выдержки при конечных температурах
нагрева При
нагреве всегда температура
центральной части материала
меньше
температуры поверхности
(если нагрев осуществляется внешним
источником тепловой энергии). Поэтому
для выравнивания температур по сечению
материала, а также для наиболее полного
осуществления технологических задач
тепловой обработки (изменение структуры,
гомогенизации, снятия напряжений и
т.п.) необходимо определенное
время выдержки при заданных конечных
температурах
нагрева. Чем сложнее изделие, тем сложнее
определить время выдержки,
т.к. для ее определения требуется
множество факторов (режимы нагрева,
теплофизические характеристики материла,
скорости их изменения от изменения
температуры и т.п.). Поэтому время нагрева
и выдержки часто определяют по значениям
безразмерных критериев:
– критерия Био
(Bi), который характеризует
тепловую инерционность системы;
– критерия Фурье
(Fо), который характеризует
температурную инерционность системы;
– температурного
критерия поверхности (θ), который
характеризует
температурную напряженность системы.
Время нагрева и
выдержки приближенно можно найти из
следующих эмпирических зависимостей
данных критериев:
(1.6)
где а
–
температуропроводность материала
(м2/с);
δ –
расчетная толщина нагреваемого тела
(расстояние от поверхности до центра)
(м);
Тпечи;
;
–
температуры печи, поверхности материала
в конце и начале нагрева соответственно
(К);
–
суммарный коэффициент теплоотдачи
;
λ – коэффициент
теплопроводности материала
;
сср
– средняя
удельная теплоемкость материала
;
ρ –
плотность материала (кг/м3).
Теплофизические
характеристики основных литейных
сплавов, материалов литейных форм и
иных материалов, используемых в литейном
производстве, представлены в приложении
А.
Рассмотрим, в
качестве примера, режимы нагрева для
отжига отливок из стали и чугуна.
Так, при
полном отжиге стальных отливок,
необходимо обеспечивать время
выдержки
при Тк
(1223-1323К) около
1 часа
на каждые 25 мм их толщины стенок. А, при
высокотемпературном
отжиге
отливок из ЧПГ, время выдержки при Тк
(1113-1173К)
зависит от содержания цементита в
структуре чугуна (который должен
полностью разложиться) и колеблется от
0,5 до 5,0 час.
С теплотехнической
точки зрения все изделия, подвергаемые
термической обработке, подразделяются
на термически «тонкие» и термически
«массивные».
В
термически «тонких» телах,
при их нагреве, перепадом
температур между центром и поверхностью
изделия можно пренебречь,
т.е. можно принимать распределение
температуры по сечению изделия
равномерным.
В термически
«массивных» телах
перепад температур составляет значительную
величину и пренебречь
им нельзя
при выборе скорости нагрева.
Условное разделение
тел на термически “тонкие” или
термически «массивные» производят по
значению безразмерного критерия Био:
,
(1.7)
где δ
– расстояние
(толщина) от центра до поверхности (м);
λ –
коэффициент теплопроводности
;
α –
коэффициент теплоотдачи
.
Величина δ/λ
представляет
собой тепловое
сопротивление нагреваемого
(охлаждаемого) материала
(его называют внутренним). Величина 1/α
– представляет
собой тепловое
сопротивление
на пути переноса
теплоты от теплоносителя к поверхности
материала
(это тепловое сопротивление называют
внешним по отношению к материалу).
Следовательно, число
Вi
можно
охарактеризовать как отношение
внутреннего теплового сопротивления
изделия при нагреве к внешнему.
Чем меньше величина δ/λ
и больше
1/α,
тем меньше
перепад температур по сечению изделия.
Увеличение δ/λ
и снижение
1/α приводят
к росту
перепада температур
и, если этот перепад значителен, тело
следует отнести к
классу «массивных».
Расчеты показывают, что принадлежность
тел к классу «тонких» определяется
значениями критерия Био в пределах:
Вi = (0÷0,25).
Принадлежность к
«массивным» телам проявляется при
значениях Био:
Вi >0,5.
Область 0,25 ≤ Вi
≤ 0,5 является
переходной.
Рассмотрим нагрев
изделий с учетом значения критерия Био
при постоянной температуре температурного
поля.
Нагрев термически
“тонких” тел при постоянной
температуре.
При
постоянной температуре
в рабочем пространстве печи (Тпечи
– const) время
нагрева термически “тонких” тел
зависит только
от интенсивности внешнего теплообмена.
В данном случае изменения температуры
тела
за время (τ)
можно
определить из следующей эмпирической
зависимости:
(1.8)
где Тпечи;
– температуры
печи и начальная изделия (К);
F –
площадь поверхности изделия (м2);
τ –
время нагрева (с)
m –
масса изделия (кг);
сср
– средняя
удельная теплоемкость материала изделия
– средний суммарный
коэффициент теплоотдачи за период
нагрева
.
Исходя из данной
эмпирической зависимости, можно найти
продолжительность окончательного
нагрева изделия (τк)
при его
нагреве до конечной температуры
(1.9)
Нагрев термически
“массивных” тел при постоянной
температуре.
Расчет
нагрева “массивных” тел
основывается на решениях задач
теплопроводности для нестационарного
температурного поля. В частности при
нагреве “массивных” тел в температурном
поле с Т=const
температурную
скорость нагрева и продолжительность
нагрева можно найти через значения
безразмерных критериев нагрева (Био,
Фурье и температурного) по эмпирическим
зависимостям (1.6).
Расчет ведется в
следующей последовательности.
1. Находят
значение безразмерного критерия Био
(Bi) по
уравнению (1.6).
2. Находят безразмерный
температурный критерий поверхности
нагреваемого изделия, при нагреве от
начальной температуры
до
конечной
температуры
:
(1.10)
3. По значениям
критериев θпов
и Вi,
пользуясь специальными номограммами
для расчета нагрева Д.В. Будрина, находим
значение безразмерного критерия Фурье
(Fо).
4. По значениям
критериев Fо
и Вi,
пользуясь номограммами Д.В. Будрина,
находим безразмерный температурный
критерий центра нагреваемого изделия
(θц).
5. По значению
температурного критерия центра (θц)
находят
конечную температуру нагрева центра
:
(1.11)
6. Находят
разность конечных температур нагрева
поверхности и центра
изделия:
(1.12)
7. Находят
температуропроводность
изделия
(а) по
уравнению (1.6).
8. Находят конечное
время нагрева
(τк),
исходя из значений критерия Фурье (Fо),
температуропроводности (а)
и расчетной
толщины нагреваемого тела (δ),
по уравнению (1.6).
Количество
теплоты, необходимое для проведения
тепловой обработки.
Любая тепловая
обработка материала, связанная с его
нагревом до определенной конечной
температуры (Тк),
возможна только при
передаче ему определенного количества
теплоты
(полезная теплота нагрева, Qп).
Данное количество
теплоты зависит:
– от
разности температур
нагрева (ΔТ
= Тк – Тн);
– от
массы нагреваемого изделия
или от массовой (объемной) производительности
тепловой обработки;
– от
теплофизических характеристик материала
или изделий (теплоемкости, скрытых
теплот плавления, испарения и т.п.).
Полезную теплоту
для обеспечения нагрева материала можно
определить по уравнению:
QП
= М ·(сср.к.
· Тк – сср.н.·
Тн) = М · ΔН,
(Дж или Вт)
(1.13)
где сср.к.и
сср.н
– средние
удельные теплоемкости нагреваемого
материала при Тк
и Тн
соответственно
;
М –
масса нагреваемого материала (кг
или кг/с);
ΔН –
изменение энтальпии (теплосодержания)
материала при его нагреве от Тн
до Тк
(Дж/кг);
Тк и
Тн –
температуры материала в конечный и
начальный период нагрева соответственно
(К).
Удельная
теплоемкость –
это количество
теплоты, необходимое для нагрева тела,
массой в 1 кг,
на 1 градус (К). Различают
удельные теплоемкости
при изобарном или изохорном процессе.
Известно, что при изобарном процессе
(Р = const) удельная теплоемкость – есть
функция температуры. Поэтому в теплотехнике
часто пользуются значениями средней
теплоемкости в пределах изменения
температур до (Тк).
Обычно используются
значения средних удельных теплоемкостей
при изобарных процессах (сср),
т.к. в печах термодинамические процессы
происходят в основном при постоянном
давлении (Р ≈ 100 кПа), или при незначительном
его изменении.
При расчетах,
связанных с газообразными веществами,
используются объемные средние теплоемкости
изобарного процесса (Дж/м3
· град).
Энтальпия –
в данном случае, это количество
тепловой энергии, которое содержится
в материале массой 1 кг,
участвующем в термодинамическом процессе
(в расчетах значение энтальпии приняты
при нормальном атмосферном давлении Р
≈ 100 кПа) и имеющем определенную
температуру (Тм). Для газов часто значение
энтальпии относят к 1 м3.
При этом объем газов должен быть приведен
к нормальным условиям.
Изменение энтальпии
материала можно определить по следующей
формуле:
ΔН = Нк – Нн.
(1.14)
Если давление в
печи будет постоянным, равным атмосферному
(Р = Р0
= const),
то:
Нк = сср.к.
· Тк; Нн = сср.н.·
Тн, (1.15)
где Нк
и Нн
– значения
энтальпий материала при Тк
и Тн
(Дж/кг).
Следует напомнить,
что значения средних удельных теплоемкостей
и иных теплофизических свойств основных
материалов, подвергаемых тепловой
обработке в литейном производстве
(металлов, сплавов, формовочных материалов
и изделий, и т.д.), представлены в приложении
А.
Если в процессе
нагрева происходит изменение агрегатного
состояния материала или его составных
компонентов, то на данный процесс также
затрачивается определенное количество
теплоты, которое должно учитываться
при определении значения полезно
затрачиваемой теплоты (Qп).
Количество теплоты, затрачиваемое на
изменение агрегатного состояния можно
определить по следующей формуле:
Qагр.
= qагр.
· М, (Дж
или Вт),
(1.16)
где qагр.
– удельная
скрытая теплота агрегатного превращения
(плавления, испарения, кристаллизации
или конденсации) (Дж/кг);
М –
масса компонента материала, меняющего
агрегатное состояние (кг
или кг/с).
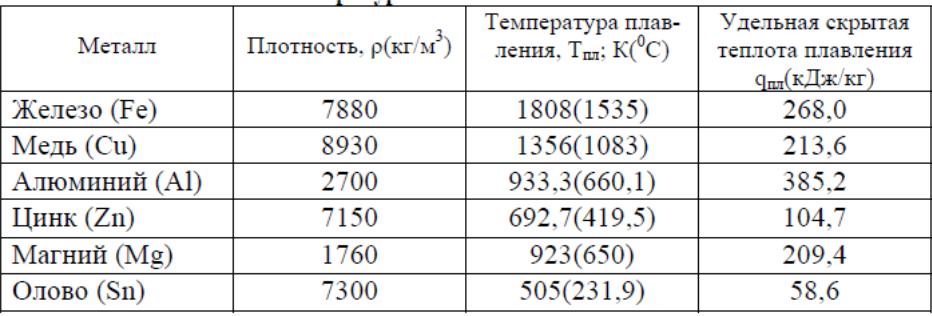
Удельная скрытая
теплота является одной из теплофизических
характеристик материала. В качестве
примера, в табл. 1.1 приведены значения
удельных скрытых теплот плавления для
некоторых чистых металлов.
Каждая печь, как
тепловой агрегат, имеет определенный
тепловой к.п.д. (η). Поэтому необходимое
количество теплоты для осуществления
нагрева будет равно:
(Дж или Вт)
(1.17)
Таблица 1.1.
Температуры и
теплоты плавления металлов.
Температурная
скорость охлаждения
Для определенных
процессов тепловой обработки требуется
вполне определенное значение температурной
скорости охлаждения материала (особенно
в процессах термообработки).
Например,
при низкотемпературном отжиге (старении)
заготовок из ВЧШГ охлаждение, после
выдержки при Тк = 773-873 К, ведут медленно
с температурной скоростью 20-50 град/ч до
температуры 573 К.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как узнать за сколько времени вещество нагреется до определенной температуры
Мыслитель
(6445),
закрыт
12 лет назад
Марина Киквадзе
Профи
(958)
12 лет назад
если считать, что потерь от нагревателя не происходит, то все тепло, выделяемое нагревателем идет на повышение температуры. Qнагр = Q масла, Q масла=с*m*Δt,
Δt = 1К или 1С, это без разницы,
Qнагревателя = Р*t
с*m*Δt = Р*t
t = с*m*Δt / Р
OdyМыслитель (6445)
12 лет назад
Спасибо огромное! Только подскажите что такое “с” и “Р”? И можно ли подставлять в формулу значения в ватах, джоулях и килограмах? Или нужно переводить?
OdyМыслитель (6445)
12 лет назад
У меня малое значение выходит. Получаеться что трансформаторное масло 17 кг нагреется, при мощности 250 Вт, на 1 градус менее чем за секунду. А до 70 тогда менее минуты. Помогите, пожалуйста )
OdyМыслитель (6445)
12 лет назад
Удельная теплоемкость 1,46 Дж/г*К
На грам… вот где я ошибся…
OdyМыслитель (6445)
12 лет назад
Получается около 2-х минут будет нагреваться на 1 градус, а это значит что до 70 градусов, масло нагрется за 2 х 50 = 100 минут? (50, так как температура воздуха около 20 градусов)
Марго
Ученик
(206)
12 лет назад
На фиг Кельвинов, узнавайте опытным путем!
OdyМыслитель (6445)
12 лет назад
Если бы это было так просто, я бы сейчас не парилься с расчетами.
Хотя если поможете достать литров 20 трансформаторного масло, желательно на шару (для расчетов), то буду благодарен!
Серёга
Мыслитель
(6658)
12 лет назад
Возьмите учебник по физике за 7-8 классы или посетите портал естественных наук. Такие задачи рассматриваются в школьной программе, ну или просто ждите ответа на вопрос здесь.
При изучении механики нас интересовало движение тел. Теперь мы рассмотрим явления, связанные с изменением свойств покоящихся тел. Мы будем изучать нагревание и охлаждение воздуха, таяние льда, плавление металлов, кипение воды и т. д. Подобные явления называют тепловыми явлениями.
Мы знаем, что при нагревании холодная вода сначала становится теплой, а затем горячей. Вынутая из пламени металлическая деталь постепенно охлаждается. Воздух, окружающий батареи с горячей водой, нагревается и т. д.
Словами «холодный», «теплый», «горячий» мы обозначаем тепловое состояние тел. Величиной, характеризующей тепловое состояние тел, является температура.
Всем известно, что температура горячей воды выше температуры холодной. Зимой температура воздуха на улице ниже, чем летом.
Приборы, служащие для измерения температуры, называются термометрами. Один из них изображен на рисунке 58. Действие такого термометра основано на тепловом расширении вещества. При нагревании столбик используемого в термометре вещества (например, ртути или спирта) увеличивается, при охлаждении уменьшается Использующиеся в быту термометры позволяют выразить температуру вещества в градусах Цельсия (°С).
А. Цельсий (1701 —1744) —шведский ученый, предложивший использовать стоградусную шкалу температур. В температурной шкале Цельсия за нуль (с середины XVIII в.) принимается температура тающего льда, а за 100 градусов — температура кипения воды при нормальном атмосферном давлении. Некоторые из температур, встречающиеся в при-Рис. 58 роде и технике, можно найти в таблице 7.
Следует помнить, что любой термометр всегда показывает свою собственную температуру. Для определения температуры среды термометр следует поместить в эту среду и подождать до тех пор, пока температура прибора не перестанет изменяться, приняв значение, равное температуре окружающей среды. При изменении температуры среды будет изменяться и температура термометра.
Несколько иначе действует медицинский термометр, предназначенный для измерения температуры тела человека. Он относится к так называемым максимальным термометрам, фиксирующим наибольшую температуру, до которой они были нагреты. Измерив свою собственную температуру, вы можете заметить, что, оказавшись в более холодной (по сравнению с человеческим телом) среде, медицинский термометр продолжает показывать прежнее значение. Чтобы вернуть столбик ртути в исходное состояние, этот термометр необходимо встряхнуть.
С лабораторным термометром, используемым для измерения температуры среды, этого делать не нужно.
Первый жидкостный термометр был изобретен в 1631 г. французским физиком Ж. Реем. Однако, научившись измерять температуру, люди не понимали, что же именно они измеряют. Вопрос о том, что такое температура, оказался очень сложным. Чем, например, горячая вода отличается от холодной? В течение долгого времени на этот вопрос не было ясного ответа.
Сегодня мы знаем, что при любой температуре вода состоит из одних и тех же молекул. Тогда что именно изменяется в воде при увеличении ее температуры?
Обратимся к опыту. Возьмем два куска сахара и один из них бросим в холодную воду, а другой — в кипяток. Мы увидим, что в горячей воде сахар растворится значительно быстрее. Растворение происходит из-за диффузии. Таким образом, диффузия при более высокой температуре происходит быстрее, чем при низкой.
Но причиной диффузии является движение молекул. Значит, между скоростью движения молекул и температурой тела есть связь: в теле с большей температурой молекулы движутся быстрее.
Например, средняя скорость молекул кислорода при 0 °С составляет 425 м/с, а при 20 °С она равна 440 м/с. Подчеркнем, что температура определяется именно средней скоростью молекул. Скорости движения отдельных молекул тела отличаются друг от друга и при заданной температуре могут быть как больше средней, так и меньше ее.
Но температура зависит не только от средней скорости молекул. Так, например, кислород, средняя скорость движения молекул которого составляет 440 м/с, имеет температуру 20 °С, а азот при той же средней скорости молекул имеет температуру 16 °С. Меньшая температура азота обусловлена тем, что молекулы азота легче молекул кислорода. Таким образом, температура вещества определяется не только средней скоростью движения его молекул, но и их массой.
Мы знаем величины, которые зависят как от скорости, так и от массы частицы. Это — импульс и кинетическая энергия. Учеными установлено, что именно кинетическая энергия молекул определяет температуру тела:
температура является мерой средней кинетической энергии частиц тела; чем больше эта энергия, тем выше температура тела.
Итак, при нагревании тел средняя кинетическая энергия молекул увеличивается, и они начинают двигаться быстрее; при охлаждении энергия молекул уменьшается, и они начинают двигаться медленнее.
Беспорядочное движение частиц, из которых состоят тела, называют тепловым движением. Тепловое движение отличается от обычного механического движения тем, что его интенсивность зависит от температуры тела и в нем всегда участвует очень много частиц, движущихся по очень сложным и запутанным траекториям.
1. Какие тепловые явления вы знаете? 2. Как протекает диффузия при разных температурах? 3. Как температура вещества зависит от средней скорости молекул и их массы? 4. Мерой чего является температура тела? 5. Чем отличается горячая вода от холодной? 6. В каком растворе — горячем или голодном — быстрее просаливаются огурцы? Почему? 7. Что такое тепловое движение? Почему оно так называется? Чем оно отличается от механического движения тел? 8. На чем основано действие термометров? 9. Когда и кем был изобретен первый жидкостный термометр?