Для правильного расчета должно быть известно назначение трубопровода: всасывающая магистраль, напорная или сливная.
Справочник по допустимой скорости жидкости в пределах этих типов магистралей приведен ниже. Расчетная скорость жидкости (м/с) должна находится в пределах этих диапазонов.
Чтобы вычислить скорость жидкости v (м/с), Вы должны ввести следующие данные:
1. Диаметр d (мм) – внутренний диаметр трубы.
2. Подача насоса Q (л/мин)
Чтобы правильно подобрать трубу для всасывающей, напорной или сливной магистралей:
1. Выберите в таблице оптимальную скорость для соответствующей магистрали (v), м/сек
2. Введите подачу насоса Q (л/мин)
Нажмите “вычислить d”
Таблица рекомендуемой скорости потока рабочей жидкости в гидроприводе:
| тип магистрали | скорость | допустимая скорость потока |
| всасывающая труба | v | от 0.5 до 1 м/с |
| сливная магистраль | v | от 1.25 до 3 м/с |
| напорная магистраль | v | 3.25 м/с при давлении более 100 бар |
| напорная магистраль | v | от 3.5 до 5 м/с при давлении более 150 бар |
| напорная магистраль | v | от 5.25 до 7 м/с при давлении более 200 бар |
| напорная магистраль | v | от 7.25 до 9 м/с при давлении более 350 бар |
Как найти скорость движения среды которую перекачивает циркуляционный насос какие данные для этого нужны?
Ученик
(24),
закрыт
6 лет назад
Евгений Павлов
Просветленный
(47824)
6 лет назад
В паспорте нет скорости, зато там есть объёмная производительность (л/мин, например). Если знать сечение трубы, то легко посчитать примерную скорость движения жидкости: если поделить секундный объём (куб. м в секунду) на площадь сечения в квадратных метрах, то получится величина скорости в метрах в секунду.
Основная погрешность будет, если диаметр трубы отличается от диаметра выходного патрубка насоса (и от высоты много зависит, остальные погрешности чуть меньше), тогда реальную объёмную производительность надо будет как-то померить. Например, расходомером или просто ведром в самой верхней точке системы – таким нехитрым способом учтутся все параметры, типа напора, вязкости, температурных коэффициентов и т. д..
Сталин
Искусственный Интеллект
(243065)
6 лет назад
Это достаточно сложная задача..
Скорость ГДЕ?
Как минимум напор развиваемый насосом, площадь проточной части, в которой определяется скорость, физические свойства среды, и тип движения среды..
Объясняя на пальцах, при одинаковом напоре скорость в трубе с большим диаметром меньше скорости в трубе с маленьким диаметром..
Содержание
- Давление
- Абсолютное и относительное давление
- Напор
- Давление насоса — описание давления насоса
- Уравнение энергии для течения идеальной жидкости
- Мощность
- Полезная мощность
- КПД
- NPSH — допускаемый кавитационный запас
- Осевая нагрузка
- Радиальная нагрузка
Показатели насоса обычно описываются с помощью набора кривых, которые называются характеристиками насоса. В этой части приведено описание таких кривых и методы их анализа.
Характеристики насоса используются заказчиком для выбора насоса, соответствующего требованиям для данного применения.
Заказная спецификация содержит информацию о напоре (H) для разной подачи (Q), см. рисунок 2.1. Требования к напору и подаче определяют габаритные размеры насоса.
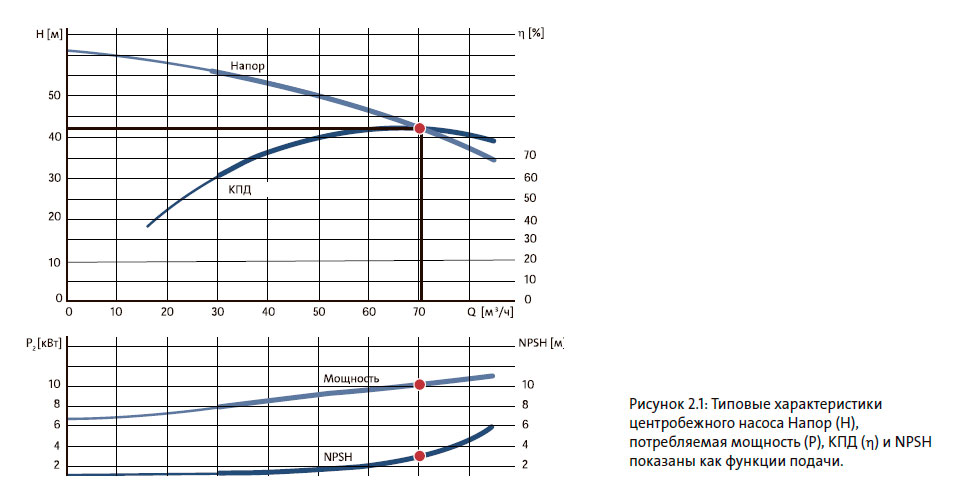
Кроме напора, в заказных спецификациях также приводится потребляемая мощность насоса (P). Потребляемая мощность используется для расчета мощности источника питания насоса. Потребляемая мощность также отображается как функция подачи.
Информация о КПД насоса (η) и NPSH также содержится в заказной спецификации. NPSH — это сокращение термина «допускаемый кавитационный запас» (Net Positive Suction Head). Кривая NPSH показывает напор на входе, который необходим для предотвращения кавитации. Кривая КПД предназначена для выбора самого экономичного насоса в определенном рабочем диапазоне. Пример характеристик в заказной спецификации приведен на рисунке 2.1.
Желаемые характеристики являются важной частью технических условий на проектирование при создании нового насоса. Подобные кривые осевых и радиальных нагрузок используются для расчета подшипников насоса.
Характеристики описывают показатели всей насосной установки, см. рисунок 2.2. Если выбран насос без электродвигателя, то для привода насоса можно использовать стандартный электродвигатель соответствующей мощности, Характеристики могут быть пересчитаны с учетом выбранного двигателя.
Для насосов, которые поставляются как с электродвигателем, так и без него, приводятся характеристики только для проточной части, то есть без электродвигателя и контроллера. Для комплектных изделий характеристики приводятся для изделия в целом.

Давление
Давление (p) выражает силу, действующую на единицу площади, и делится на статическое и динамическое давление. Сумма этих двух давлений представляет собой полное давление.

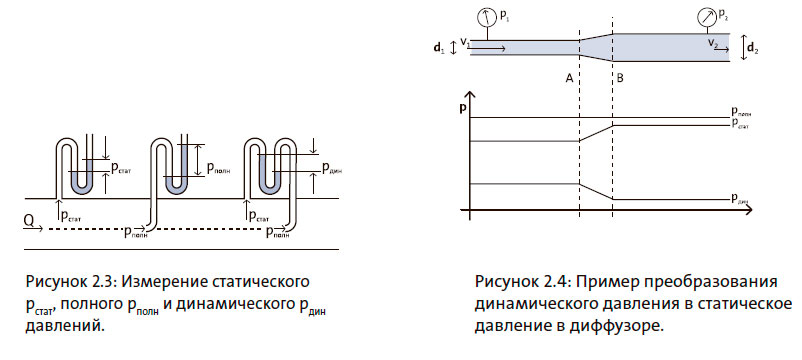
Измерение статического давления производится с помощью манометра, исключительно при неподвижной жидкости или с помощью отвода давления, установленного перпендикулярно направлению потока, см. рисунок 2.3.
Для измерения полного давления приемное отверстие отвода давления следует расположить навстречу направлению потока, см. рисунок 2.3. Динамическое давление определяется как разность между полным и статическим давлением. Такое измерение может быть выполнено с помощью трубки Пито.
Динамическое давление зависит от скорости жидкости, Динамическое давление может быть рассчитано по следующей формуле, в которой скорость (V) получена с помощью измерения, а плотность (ρ) жидкости известна:
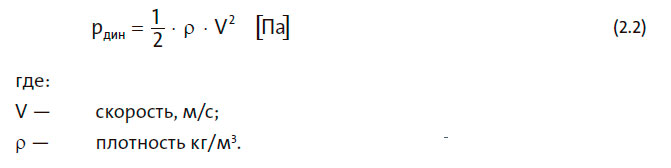
Динамическое давление может быть преобразовано в статическое, и наоборот. При течении в расширяющейся трубе происходит преобразование динамического давления в статическое, см. рисунок 2.4. Течение в трубе называется потоком в трубе, а участок трубы, в котором диаметр трубы увеличивается, называется диффузором.
Абсолютное и относительное давление
Давление может быть выражено двумя различными способами — как абсолютное или относительное давление. Абсолютное давление измеряется относительно абсолютного 0 и, таким образом, может иметь только положительное значение. Относительное давление измеряется относительно давления окружающей среды. Положительное относительное давление означает, что давление выше барометрического давления, а отрицательное относительное давление указывает на то, что давление ниже барометрического давления.
Определение абсолютной и относительной величины известно также по измерениям температуры, где абсолютная температура измеряется в Кельвинах (K), а относительная температура измеряется в градусах Цельсия (°C). Температура в Кельвинах всегда положительна и измеряется относительно абсолютного 0. В отличие от этого, температура в градусах Цельсия измеряется относительно точки замерзания воды (соответствует 273,15 K), и поэтому может быть отрицательной.
Барометрическое давление измеряется как абсолютное давление. Барометрическое давление зависит от погоды и высоты. Переход от относительного давления к абсолютному осуществляется добавлением существующего барометрического давления к измеренному относительному давлению.

На практике статическое давление измеряется с помощью манометров трех различных типов.
- Манометр абсолютного давления, например, барометр, измеряет давление относительно абсолютного 0.
- Стандартный манометр измеряет давление относительно атмосферного давления. Такой тип манометров используется чаще всего.
- Дифференциальный манометр измеряет разность давлений между двумя отводами давления независимо от барометрического давления.
Напор
На следующих страницах представлены различные характеристики.
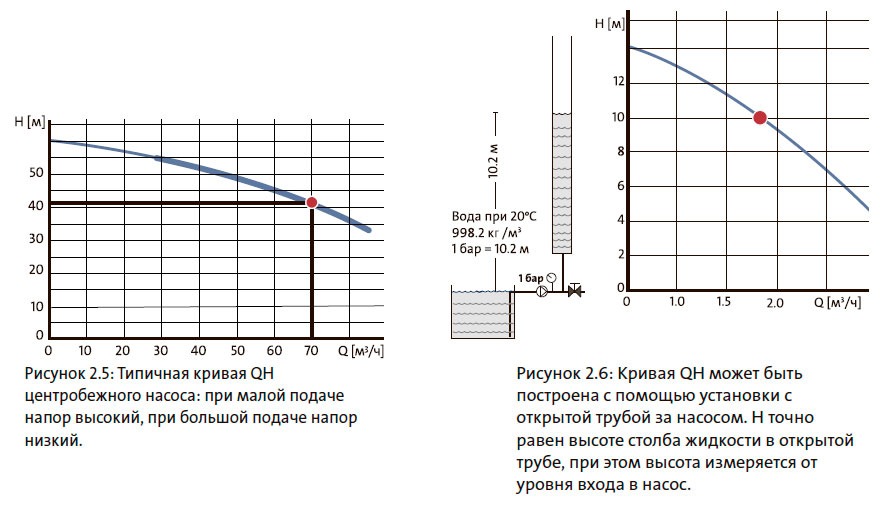
Кривая QH показывает напор (H) как функцию подачи (Q). Подача (Q) — это объем жидкости, проходящей через насос на единицу времени. Подача обычно выражается в кубических метрах в час (м3/ч), но в формулах используются кубические метры в секунду (м3/с). Типичная кривая QH показана на рисунке 2.5.
Построение кривой QH для заданного насоса производится с помощью установки, показанной на рисунке 2.6.
Насос запускается и работает с постоянной частотой вращения. При полном закрытии арматуры Q равно нулю, а H достигает максимального значения. При постепенном открытии арматуры Q увеличивается, а H уменьшается. H — это высота столба жидкости в открытой трубе за насосом. Кривая QH представляет собой последовательность точек, соответствующих парам значений Q и H, см. рисунок 2.5.
В большинстве случаев измеряется давление насоса Dpполн, а напор H рассчитывается по следующей формуле:

Кривая QH будет точно такой же, если опыт, изображенный на рисунке 2.6, провести с жидкостью, плотность которой отличается от плотности воды. Таким образом, кривая QH не зависит от перекачиваемой жидкости. Это можно объяснить с помощью теории, где доказано, что Q и H зависят от геометрии насоса и скорости вращения рабочего колеса, но не от плотности перекачиваемой жидкости.
Повышение давления в насосе можно измерить в метрах водяного столба (м вод. ст.). Метр водяного столба — это единица давления, которую нельзя путать с напором, выраженным в метрах. Как видно из таблицы физических свойств воды, при повышении температуры плотность воды существенно изменяется. Таким образом, необходимо выполнять преобразование давления в напор.
Давление насоса — описание давления насоса
Полное давление
Полное давление насоса рассчитывается как сумма трех составляющих:

Статическое давление
Статическое давление может быть измерено непосредственно с помощью датчика дифференциального давления, или можно установить датчики давления на входе и выходе насоса. В этом случае статическое давление может быть найдено по формуле:
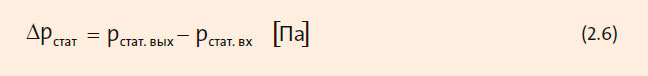
Динамическое давление
Динамическое давление (разность динамических давлений между входом и выходом насоса) определяется по следующей формуле:
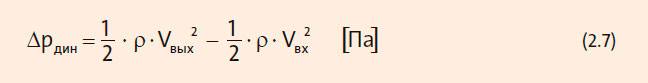
На практике при испытаниях насоса измерение динамического давления и скорости потока на входе и выходе насоса не производится. Вместо этого динамическое давление определяется расчетным методом на основе расхода жидкости и диаметра трубы на входе и выходе насоса:
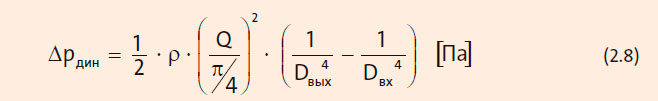
Как следует из формулы, динамическое давление равно нулю, если диаметры трубы до и после насоса одинаковы.
Разность барометрических давлений
Разность барометрических давлений в точках установки датчиков давления на входе и выходе насоса может быть определена следующим образом:

где:
Δz — разность высот между точками установки манометра, соединенного с трубой на выходе, и манометра, соединенного с трубой на входе.
Разность барометрических давлений имеет значение, только если Δz не равно нулю. Таким образом, положение отводов давления на трубе не имеет значения при определении разности барометрических давлений.
Если для измерения статического давления используется дифференциальный манометр, то разность барометрических давлений принимается равной нулю.
Уравнение энергии для течения идеальной жидкости
Согласно уравнению энергии для течения идеальной жидкости сумма энергии давления, кинетической энергии и потенциальной энергии является постоянной величиной. Это уравнение называется уравнением Бернулли по имени швейцарского физика Даниэля Бернулли.
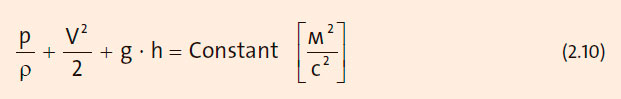
Уравнение Бернулли справедливо при следующих условиях:
- 1. Течение установившееся — не изменяется со временем.
- 2. Жидкость несжимаема — справедливо для большинства жидкостей.
- 3. Течение без трения — потери на трение не учитываются.
- 4. Свободное течение — нет подвода механической энергии.
Формула (2.10) применяется для струйки жидкости или траектории частицы жидкости. Например, с помощью формулы может быть описано течение жидкости в диффузоре (2.10), но не поток через рабочее колесо, так как рабочее колесо подводит к жидкости механическую энергию.
В большинстве применений не все условия для уравнения энергии соблюдаются, Несмотря на это, уравнение может быть использовано для приблизительных вычислений.
Мощность
Кривые мощности показывают потребляемую мощность как функцию подачи, см. рисунок 2.7. Мощность выражается в ваттах (Вт). Следует различать три вида мощности, см. рисунок 2.8.
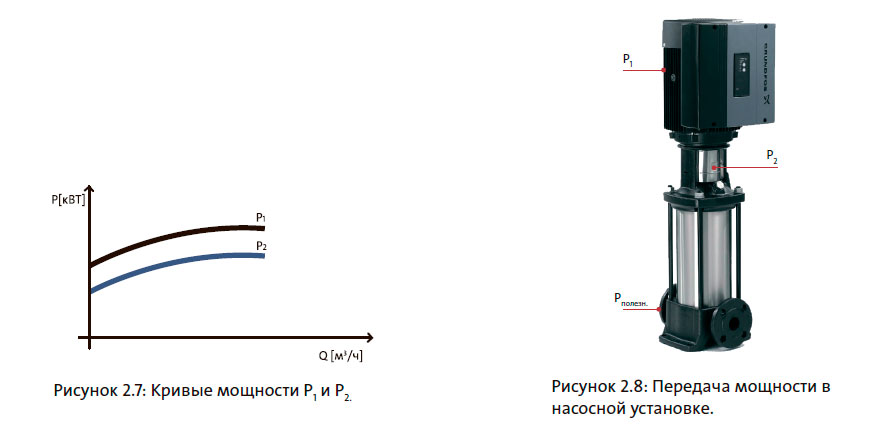
- Мощность насосной установки, передаваемая от внешнего источника к электродвигателю и контроллеру (P1).
- Мощность насоса, передаваемая электродвигателем на вал (P2).
- Полезная мощность, передаваемая от рабочего колеса насоса к жидкости (P полезн).
Потребляемая мощность зависит от плотности жидкости. Кривые мощности обычно строятся для стандартной жидкости, имеющей плотность 1000 кг/м3, что соответствует воде при температуре 4°C. Таким образом, мощность, измеренная на жидкости с другой плотностью, должна быть пересчитана.
Обычно в заказных спецификациях P1 приводится для комплектных изделий, в то время как P2 приводится для насосов, поставляемых со стандартным электродвигателем.
Частота вращения
Подача, напор и потребляемая мощность изменяются в зависимости от частоты вращения насоса. Сравнение характеристик насоса возможно только если они построены для одинаковой частоты вращения. Возможно приведение характеристик к одинаковой скорости с использованием уравнений, приведенных ниже.
Регулирование частоты вращения
При регулировании частоты вращения насоса характеристики QH, мощности и NPSH изменяются. Пересчеты характеристик насоса при изменении его частоты вращения выполняются с помощью уравнений подобия.
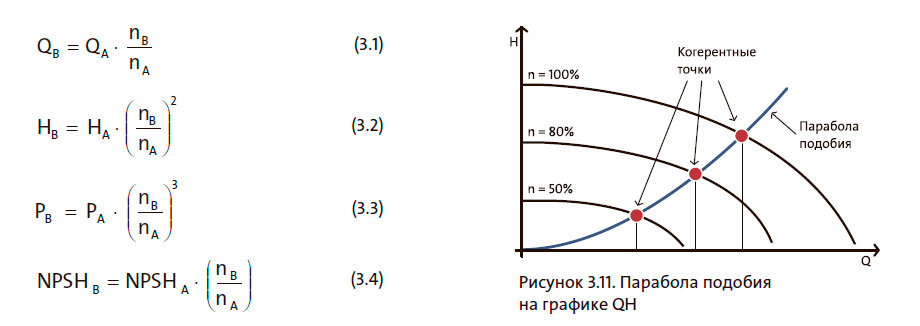
Индекс A в уравнениях указывает исходные значения, а индекс В указывает измененные значения.
Эти уравнения позволяют получить когерентные точки на параболе подобия на графике QH. Парабола подобия показана на рисунке 3.11.
На основании соотношения между характеристикой насоса и его частотой вращения могут быть получены различные регулировочные характеристики. Наиболее распространенными методами регулирования являются метод пропорционального регулирования и метод регулирования в режиме поддержания постоянного давления.
Полезная мощность
Полезная мощность (P полезн) — это мощность, передаваемая от насоса к жидкости. Как видно из следующей формулы, полезная мощность рассчитывается по подаче, напору и плотности.
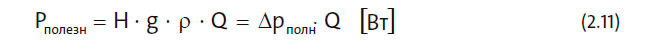
Отдельная кривая полезной мощности обычно не приводится в заказных спецификациях, однако используется для расчета КПД насоса.
КПД
КПД насосной установки (ηполн) — это отношение полезной мощности к мощности насосной установки. На рисунке 2.9 показаны кривые КПД для насоса (ηполезн) и для насосной установки, включающей электродвигатель и контроллер (ηполн).
Гидравлический КПД относится к P2 , а КПД насосной установки — к P1:
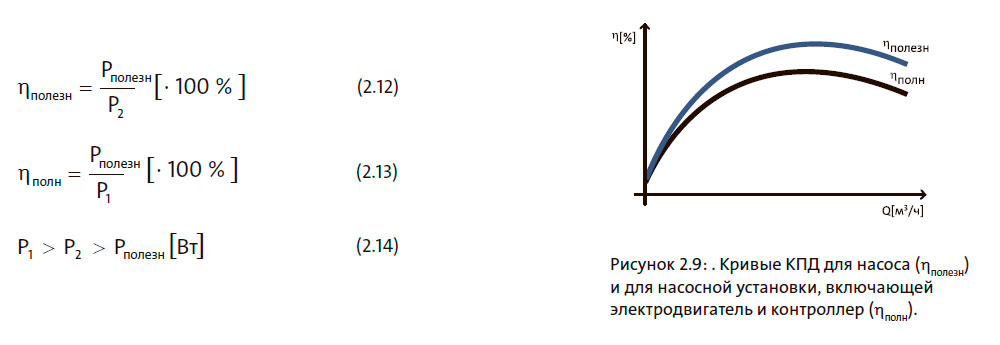
КПД всегда меньше 100 %, так как мощность насосной установки всегда больше, чем полезная мощность, вследствие потерь в контроллере, электродвигателе и насосе. КПД насосной установки (контроллер, электродвигатель и насос) является произведением отдельных КПД:

Подача, при которой насос имеет максимальный КПД, называется точкой оптимального режима или точкой наибольшего КПД (QBEP).
NPSH — допускаемый кавитационный запас
Кавитацией называется процесс образования пузырьков пара в областях, где локальное давление падает до значения давления насыщенного пара. Степень кавитации зависит от того, насколько низким будет давление в насосе. При кавитации происходит снижение напора и появление шума и вибрации.
Кавитация вначале возникает в областях наименьшего давления в насосе, чаще всего образуются на кромках лопаток на входе в рабочее колесо, см. рисунок 2.10.
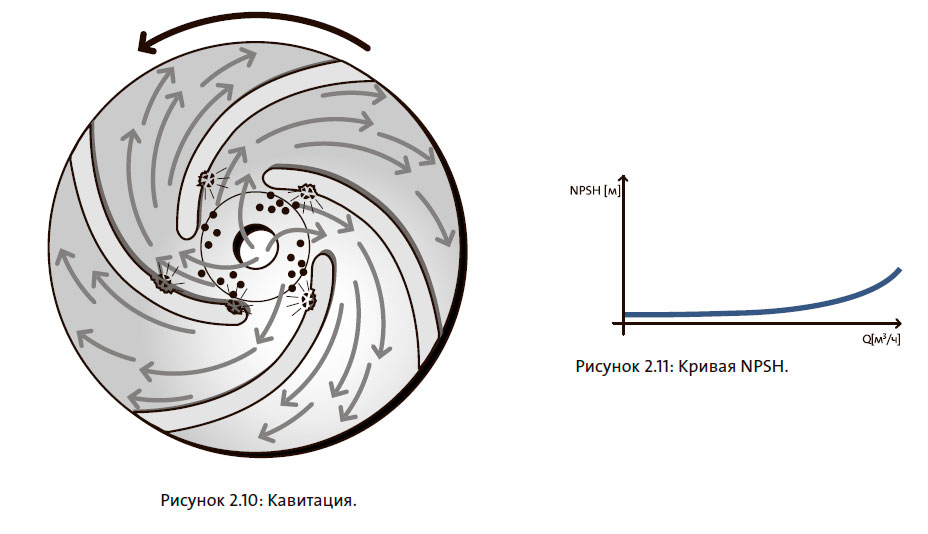
Значение NPSH — абсолютное и всегда положительное. NPSH измеряется в метрах, как напор, см. рисунок 2.11. Так как NPSH измеряется в метрах, нет необходимости учитывать плотность различных жидкостей.
Существуют два различных значения NPSH: NPSHR и NPSHA.
NPSHA обозначает имеющийся NPSH и определяет, насколько близко к парообразованию находится жидкость во всасывающем трубопроводе. NPSHA определяется по формуле:

NPSHR обозначает требуемый NPSH и выражает наименьшее значение NPSH, требуемое для приемлемой работы насоса. Абсолютное давление на входе может быть рассчитано по заданному значению NPSHR и давлению насыщенных паров жидкости путем подстановки в формулу (2.16) NPSHR вместо NPSHA.
Чтобы определить, может ли насос быть безопасно установлен в систему, следует найти NPSHA и NPSHR для наибольших значений подачи и температуры в пределах рабочего диапазона.
Рекомендуется добавить минимальный запас безопасности 0,5 м. В зависимости от применения может понадобиться больший запас безопасности. Например, для применений, чувствительных к шуму, или для мощных насосов, таких как питательные насосы котлов, европейская ассоциация производителей насосов рекомендует применять к значению NPSH3% коэффициент безопасности SA=1,2 – 2,0.
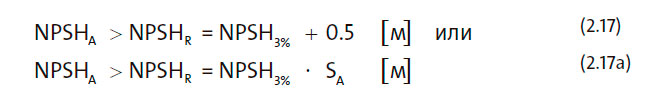
Риск кавитации в системах может быть снижен или исключен с помощью следующих мер:
- установка насоса ниже по отношению к уровню жидкости в открытых системах;
- повышение давления в закрытых системах;
- уменьшение длины линии всасывания для снижения потерь на трение;
- увеличение площади поперечного сечения всасывающего трубопровода для снижения скорости движения жидкости и, как следствие, уменьшения потерь на трение;
- исключение локальных падений давления, возникающих вследствие изгибов и других препятствий во всасывающем трубопроводе;
- снижение температуры жидкости для уменьшения давления паров.
Следующие два примера показывают, как рассчитывается NPSH.
Пример 2.1 Насос для подачи жидкости из колодца
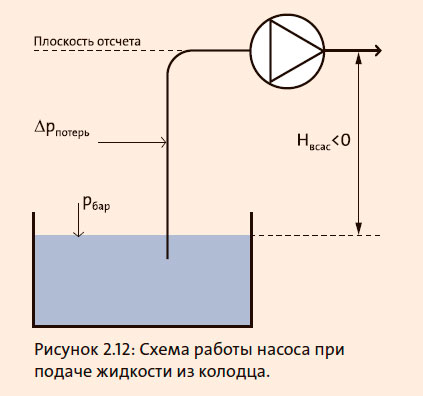
Насос должен подавать жидкость из резервуара, уровень воды в котором на 3 метра ниже уровня насоса. Для расчета значения NPSHA необходимо знать потери на трение во всасывающем трубопроводе, температуру воды и барометрическое давление, см. рисунок 2.12.
Температура воды 40°C
Барометрическое давление 101,3 кПа.
Потери давления во всасывающем трубопроводе при существующей подаче 3,5 кПа.
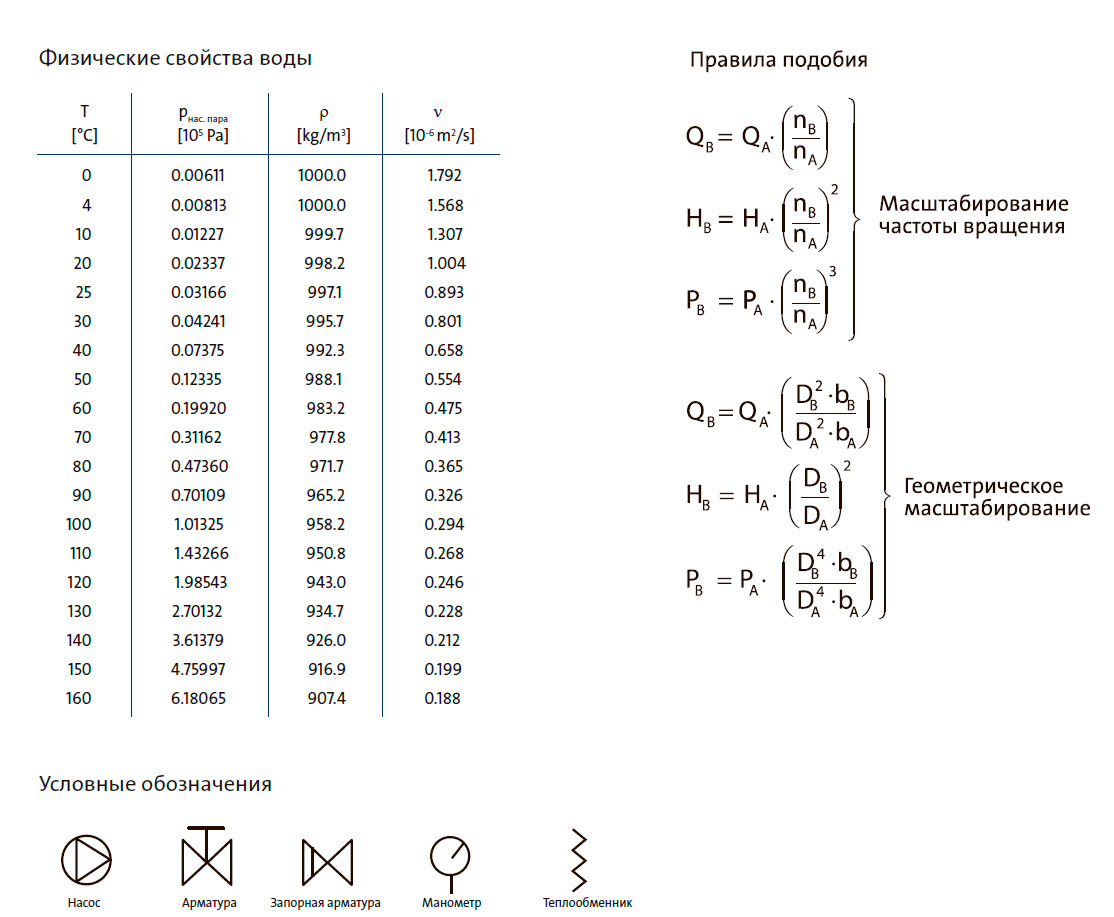
При температуре воды 40°C давление паров равно 7,37 кПа, а ρ равно 992,2 кг/м3.
Значения взяты из таблицы «Физические свойства воды» в конце статьи.
Для этой системы выражение NPSHA в формуле (2.16) может быть записано в следующем виде:
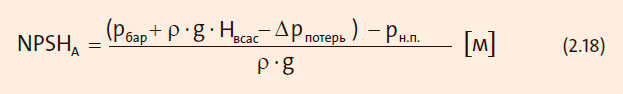
Hвсас— уровень воды относительно насоса. Hвсас может быть выше или ниже насоса и выражается в метрах. В этой системе уровень воды находится ниже насоса. Таким образом, Hвсас отрицательно, Hвсас = –3 м.
Значение NPSHA для системы:

Насос, предназначенный для работы в рассматриваемой системе, должен иметь значение NPSHR меньше, чем 6,3 м минус запас безопасности 0,5 м. Таким образом, при существующей подаче для насоса требуется значение NPSHR меньшее, чем 6,3 – 0,5 = 5,8 м.
Пример 2.2 Насос в закрытой системе
В закрытой системе отсутствует свободная поверхность воды для использования в качестве плоскости отсчета. Этот пример показывает, как датчик давления, расположенный выше плоскости отсчета, может использоваться для определения абсолютного давления в линии всасывания, см. рисунок 2.13.
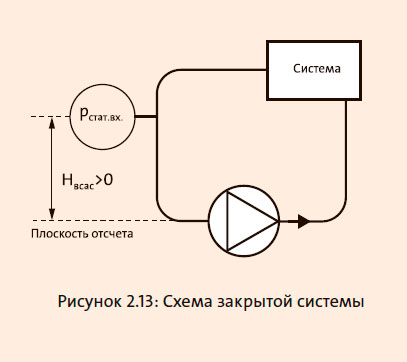
Измеренное относительное статическое давление на стороне всасывания pстат.вх = -27.9 кПа. Таким образом, в точке установки манометра имеется отрицательное давление. Манометр установлен выше насоса. Следовательно, разность между высотой манометра и высотой входа в рабочее колесо имеет положительное значение Hвсас = +3 м. Скорость в трубе, где измеряется давление, создает дополнительное динамическое давление 500 Па.
Барометрическое давление 101 кПа.
Рассчитанные потери на трение в трубах между точкой измерения (pстат.вх.) и насосом Hпотерь труб. = 1м.
Температура системы 80°C.
Давление паров pн.п. = 47.4 кПа, плотность ρ = 973 кг/м3, значения взяты из таблицы «Физические свойства воды».
Для этой системы формула 2.16 для NPSHA имеет следующий вид:
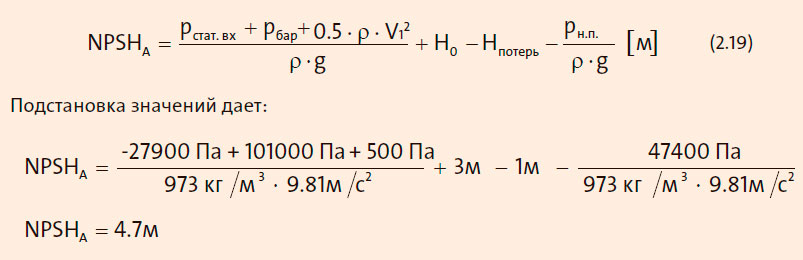
Несмотря на отрицательное давление в системе, значение NPSHA для существующего расхода превышает 4 м.
Осевая нагрузка
Осевая нагрузка является суммой сил, действующих на вал в осевом направлении, см. рисунок 2.14. Осевая нагрузка в основном возникает вследствие
разности давлений на переднем и заднем диске рабочего колеса.
Значение и направление осевой нагрузки может использоваться для определения типоразмера подшипников и конструкции электродвигателя.
Насосы с нагрузкой, направленной вверх, требуют применения фиксированных подшипников. Дополнительно к осевой нагрузке необходимо учесть силы,
действующие на вал вследствие давления в системе. Пример кривой осевой нагрузки представлен на рисунке 2.15.
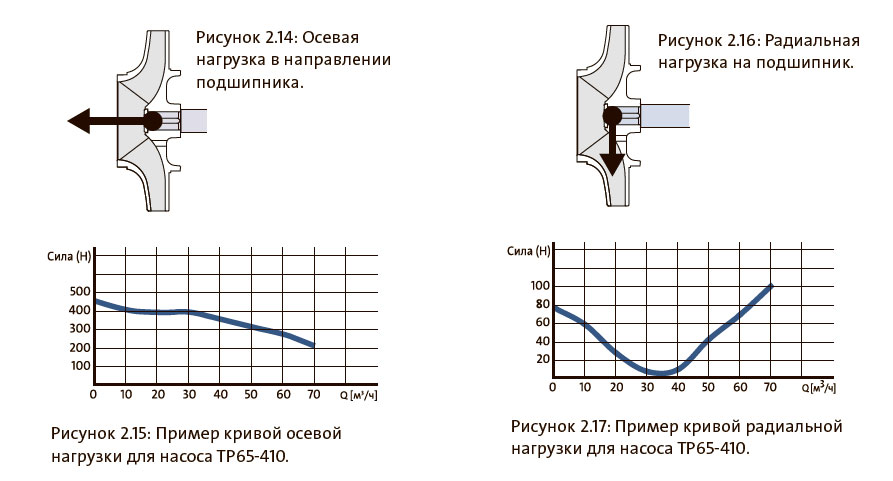
Осевая нагрузка связана с напором и поэтому пропорциональна квадрату скорости.
Радиальная нагрузка
Радиальная нагрузка является суммой сил, действующих на вал в радиальном направлении, см. рисунок 2.16. Гидравлическая радиальная нагрузка возникает
вследствие разности давлений в спиральной камере. Значение и направление изменяются в зависимости от подачи. Силы минимальны при расчетном
режиме, см. рисунок 2.17. Для правильного выбора радиального подшипника важно знать значение радиальной нагрузки.
Выводы
В статье приведено объяснение терминов, применяемых для описания показателей насоса, и приведены кривые напора, мощности, КПД, NPSH и действия нагрузок. Кроме того, два термина — напор и NPSH — были пояснены на примерах расчета.
Литература
Центробежный насос – GRUNDFOS [2012]
www.grundfos.com
Удельная скорость концепция, разработанная для водяных турбин в 1915 году, который впоследствии был применен для центробежных насосов (Степанов, 1948). Конкретные скорости способ «нормализации» выполнения этих гидравлических машин.
Часто используемых уравнения для определенной скорости выглядит как показано на рисунке.
Когда я впервые познакомился с определенной скоростью, я должен признаться, что не впечатлило. Мне показалось, что концепция может быть полезна для насоса дизайнеров, но я видел никакой ценности для конечного пользователя. Позже я узнал, что концепция имеет важное значение для дизайнера, и, поскольку он указывает на форму головы, мощность и эффективность кривых и максимально достижимой эффективности, но и стоимость для конечных пользователей.
Одно из определений конкретных скорости является то, что скорость, с которой моделируемой насос будет работать для получения одной ногой голову, когда насосная одного галлона в минуту, но я считаю, что определение неловко.
Я предпочитаю думать о нем, как порядковый номер. В Европе, удельная скорость иногда называют “форма номер”, и я предпочитаю, чтобы имя. Это указывает на форму кривых производительности, а также определяет, в значительной степени, профилем формы рабочего колеса.
Рабочее колесо с низкой удельной скорости имеет тонкий профиль (кожухи близко друг к другу) и большой внешний диаметр (OD) по отношению к диаметру глаза. Рабочее колесо с высокой удельной скорости имеет толстый профиль (кожухи далеко друг от друга) и имеет диаметр глаза, что ближе по размерам с рабочим колесом диаметром.
Рисунок помогает проиллюстрировать эту концепцию. График был разработан лет назад группой Уортингтон и широко используется в промышленности. Обратите внимание, что значения удельной скорости в единицах США, приведены в таблице в нижней части графика. Небольшие рисунки ниже график показывает профилей колес, которые соответствуют конкретные цифры скорости.
Небольшой кривых производительности в верхней части графика иллюстрирует типичную форму корреспондент производительность кривые значения удельной скорости. Обратите внимание, что насосы с низкой удельной скорости имеют плоскую кривую головы, иногда с небольшой спад на запорный (нулевой мощности). Такой спад не делает насос неустойчивой. Кривую мощности крутой. Это значительно увеличивает с запорной для лучшей эффективности точка (BEP).
В средние значения Н.С., начальник кривая постоянно поднимается до отключения воды, и кривая мощности мало меняется с запорными в НПД. Когда NS превосходит 5000, наклон кривой мощности меняет, с максимальным значением находясь на запорные, и голова кривая очень крутой, с запорным значение быть столько, сколько три раза BEP значение. (Не начинайте один из этих парней с выпускной клапан закрыт.)
ВыводДля тех, кто хотел бы увидеть вывод Н.С., предлагается следующее. Я использую то, что называется “моделирование закон” или “модельный закон” или “факторинг закона». Этот «закон» используется, когда дизайнер хочет, чтобы “модель” насос с одним из разного размера.
Каждое измерение насоса умножается на тот же фактор, моделирование факторов, существующих насоса обозначается индексом «1» и новый насос с индексом затем “F”. “2”.:
Полученная является определенной скоростью. Когда насос моделируется с другой, как насосы имеют те же конкретные скорости.
Посылка и безразмерныеОн обычно говорил, что конкретные безразмерные скорости, но обычно это не так. В США с выше единицы, это не безразмерные. Это можно сделать безразмерные, однако, путем преобразования скорости рад / сек, возможность кубических футов / сек и, умножив голову гравитационная постоянная “G”.
NS значений на графике Уортингтон работать от 500 до 15000. Что бы значения, если бы мы были перейти на безразмерные числа? Мы должны разделить N на 9,55, чтобы преобразовать в радианы / сек. Вопрос должен быть разделен на 449, чтобы преобразовать в ft3/second и H следует умножить на 32,2.
Результат говорит нам, что для преобразования единиц США в безразмерных значений требует, чтобы США значений NS делится на 2735. Таким образом, 500 станут около 1/5, 15000 станут около 5, а безразмерные значения 1,0 упадет очень близко к центру графика, в котором максимальной эффективности достигают своего пика.
Есть ли смысл в максимальной эффективностью происходящих где безразмерные NS равен 1,0? Я не знаю, но он уверен, кажется, счастливая случайность.
СсылкиСтепанов, AJ, центробежные и осевые насосы, John Wiley & Sons, Нью-Йорк, 1948.Степанов, AJ, насосы и вентиляторы – двухфазного потока, John Wiley & Sons, Нью-Йорк, 1965 год.
ПримечанияРеакции турбины, в основном, только центробежный насос работает в обратном направлении, с жидкостью толкают обратно через него.Если речь идет о двойной крыльчаткой всасывания, не делим на 2. При определенной скорости всасывания, мы делим емкость 2, но не для (разряда) определенной скоростью.
Насосы и системы, сентябрь 2011
Основное уравнение центробежных насосов
(УРАВНЕНИЕ ЭЙЛЕРА)
Основное
уравнение центробежного насоса впервые
в самом общем виде было получено в
1754 г. Л.
Эйлером и носит ею имя.
Рассматривая
движение жидкости внутри рабочего
колеса, сделаем следующие допущения:
насос перекачивает идеальную жидкость
в виде струй, т. е. в насосе отсутствуют
все виды потерь энергии. Число одинаковых
лопастей насоса бесконечно большое (z
= µ),
толщина их равна нулю (d=
0), а угловая
скорость вращения колеса постоянна (w=
const.).
К
рабочему колесу центробежного насоса
со скоростью Vo
жидкость подводится аксиально, т. е. в
направлении оси вала. Затем направление
струй жидкости изменяется от осевого
до радиального, перпендикулярного оси
вала, а скорость благодаря центробежной
силе увеличивается от значения V1
в пространстве между лопастями рабочего
колеса до значения V2
на выходе из колеса.
В
межлопастном пространстве рабочего
колеса при движении жидкости различают
абсолютную и относительную скорости
потока. Относительная
скорость
потока
— скорость
относительно рабочего колеса, а абсолютная
—
относительно корпуса насоса.


Рис.
Схема
движения жидкости в рабочем колесе
центробежного насоса
Абсолютная
скорость равна геометрической сумме
относительной скорости жидкости и
окружной скорости рабочего колеса.
Окружная скорость жидкости, выходящей
между лопастями рабочего колеса,
совпадает с окружной скоростью колеса
в данной точке.
Окружная
скорость жидкости (м/с) на входе в рабочее
колесо
![]()
Окружная скорость
жидкости на выходе из рабочего колеса
(м/с)
![]()
где
n—частота
вращения рабочего колеса, об/мин; D1
и D2
— внутренний
и внешний диаметры рабочего колеса, м,
w—
угловая скорость вращения рабочего
колеса рад/с
При
движении рабочего колеса частицы
жидкости движутся вдоль лопастей.
Вращаясь вместе с рабочим колесом, они
приобретают окружную скорость, а
перемещаясь вдоль лопастей
— относительную.
Абсолютная
скорость v
движения жидкости равна геометрической
сумме ее составляющих: относительной
скорости w
и окружной
u,
т. е.
v = w
+ и.
Связь
между скоростями частиц жидкости
выражается параллелограммом или
треугольниками скоростей, что позволяет
дать понятие о радиальной и окружной
составляющих абсолютной скорости.
Радиальная
составляющая
![]()
окружная
составляющая
![]()
где
a—
угол между абсолютной и окружной
скоростями (на входе рабочего колеса
a1
и на выходе a2).
Угол
b
между относительной и окружной скоростями
характеризует очертание лопастей
насоса .
Исследуем
изменение за
1 с момента
количества движения Массы жидкости т
=
rQ,
где r
— плотность
жидкости; Q—
подача насоса.
Используя
теорему механики об изменении моментов
количества движения применительно
к движению жидкости в канале рабочего
колеса, выведем основное уравнение
центробежного насоса, которое позволит
определить развиваемый насосом напор
(или давление). Эта теорема гласит:
изменение во времени главного момента
количества движения системы материальных
точек относительно некоторой оси равно
сумме моментов всех сил, действующих
на эту систему.
Момент
количества движения жидкости относительно
оси рабочего колеса во входном сечении
![]()
Момент
количества движения на выходе из рабочего
колеси
![]()
где
r1
и r2
—
расстояния от оси колеса до векторов
входной V1
и выходной
V2
скоростей
соответственно.
Согласно
определению момента системы можно
записать:
![]()
Так
как в соответствии с рис
![]()
![]()
![]()
Группы
внешних сил
— силы
тяжести, силы давления в расчетных
сечениях (входа-выхода) и со стороны
рабочего колеса и силы трения жидкости
на обтекаемых поверхностях лопастей
рабочего колеса
— действуют
на массу жидкости, заполняющей межлопастные
каналы рабочего колеса.
Момент
сил тяжести относительно оси вращения
всегда равен нулю, так как плечо этих
сил равно нулю. Момент сил давления в
расчетных сечениях по этой же причине
также равен нулю. Если силами трения
пренебрегают, то и момент сил трения
равен нулю. Тогда момент всех внешних
сил относительно оси вращения колеса
сводится к моменту Мк
динамического воздействия рабочего
колеса на протекающую через него
жидкость, т. е.
![]()
Произведение
Мк
на относительную скорость равно
произведению расхода на теоретическое
давление PT,
создаваемое насосом, т. е. равно
мощности, передаваемой жидкости рабочим
колесом. Следовательно,
![]()
Это
уравнение
можно
представить в виде
![]()
Разделив
обе его части на Q,
получим
![]()
Учитывая,
что напор Н
= Р/(pg)
и подставив
это
значение получим
![]()
Если
пренебречь силами трения, то можно
получить зависимости, называемые
основными
уравнениями лопастного насоса.
Эти уравнения
отражают зависимость теоретического
давления или напора от основных параметров
рабочего колеса. Переносные скорости
на входе в осевой насос и на выходе из
него |одинаковы, поэтому уравнение
принимает
вид
![]()
В
большинстве насосов жидкость в рабочее
колесо поступает практически радиально
и, следовательно, скорость
V1
»
0. C
учетом
вышеизложенного
![]()
или
![]()
Теоретические
давление и напор, развиваемые насосом,
тем больше, чем больше окружная скорость
на внешней окружности рабочего колеса,
т. е. чем больше его диаметр, частота
вращения и угол b2
, т. е. чем
«круче» расположены лопатки рабочего
колеса.
Действительные
давление и напор, развиваемые насосом,
меньше теоретических, так как реальные
условия работы насоса отличаются от
идеальных, принятых при выводе уравнения.
Давление, развиваемое насосом, уменьшается
главным образом из-за того, что при
конечном числе лопастей рабочего
колеса не все частицы жидкости отклоняются
равномерно, вследствие чего уменьшается
абсолютная скорость. Кроме того, часть
энергии расходуется на преодоление
гидравлических сопротивлении. Влияние
конечного числа лопастей учитывают
введением поправочного коэффициента
k
(характеризующею уменьшение окружной
составляющей скорости V2u),
уменьшение давления вследствие
гидравлических потерь
— введением
гидравлического коэффициента полезного
действия hr
. С учетом
этих поправок полное давление
Соседние файлы в папке лекции ОГИТ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
