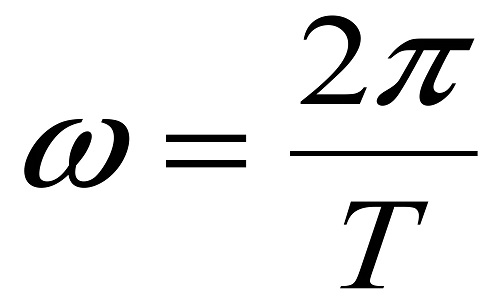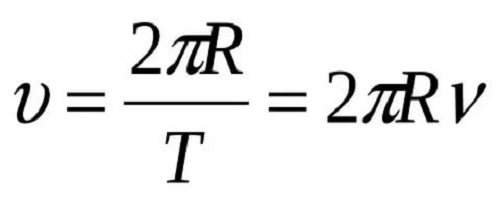Как найти скорость обращения земли

Как найти скорость обращения земли

Мы уже рассчитывали линейную и угловую скорости вращения Земли вокруг своей собственной оси. Давайте сегодня рассмотрим движение Земли вокруг Солнца, и найдем скорость этого движения. Ну, и заодно, рассмотрим три закона Кеплера. Куда без них.

Первый способ

С какой скоростью вращается Земля вокруг Солнца? Первое что приходит в голову, это воспользоваться уже знакомым уравнением для нахождения линейной скорости:

    [upsilon =frac {2pi R}{T}]

Расстояние от Земли до Солнца одна астрономическая единица или 149 597 870 700 м. Период обращения составляет один год. Если перевести это в секунды мы получим 31 536 000 с.

Подставляем это все в наше уравнение и считаем.

upsilon =frac {2*3,14 *149 597 870 700}{31536000} approx 29 790,545м/с

Второй способ

Но можно и пойти другим путем. Скорость движения Земли будет являться первой космической скоростью в поле тяготения Солнца. По этому, вспоминаем уравнение для нахождения первой космической скорости.

    [v =sqrt{frac {G*M_c}{R}}]

Где G -это гравитационная постоянная, R — расстояние от Земли до Солнца, ну и M — масса самого Солнца. Остается только взвесить Солнце и произвести расчет:

v =sqrt{frac {G*M_c}{R}} = sqrt{frac {6.67cdot 10^{-11}cdot 1.9985 cdot 10^{30}}{1.496cdot 10^{11}}}approx 29775.559 м/с

Часто для удобства скорость округляют и представляют как 30 км/с или 108 000 км/ч. Последний вариант, кстати, очень любят индусы. Так как в индуизме число 108 считается священным. Они даже число Пи, в свое время, определяли как отношение 339/108. Но вернемся к скорости.

Первый закон Кеплера

В наших расчетах мы принимали что Земля равномерно движется по окружности. Хотя в реальности это не совсем так.

Иоганн Кеплер

Иоганн Кеплер (1571 — 1630 гг).

Еще в начале XVII века немецкий астроном Иоганн Кеплер, опираясь на данные многолетних наблюдений за планетой Марс, полученные его учителем — датским астрономом Тихо Браге, заключил, что все планеты солнечной системы движутся не по окружности, а по эллипсу, в одном из фокусов которого находится Солнце. Этот закон называют первым законом Кеплера.

Все планеты Солнечной Системы движутся по эллипсу, в одном из фокусов которого находится Солнце.

Так что давайте разобраться что такое такое эллипс, и в чем его фокус.. или фокусы.

Что такое эллипс?

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

Рассмотрим все на простом примере. Берем шнурок с канцелярскими кнопками-гвоздиками на концах. Втыкаем кнопки в кусок гипсокартонна, который завалялся в гараже после ремонта.

Эллипс

Далее карандашом, опираясь на шнурок рисуем линии. Получившаяся фигура и есть эллипс, а точки куда мы втыкали кнопки называются фокусами.

Большая и малая полуось

Важными характеристиками эллипса являются его полуоси. Большая ее обычно обозначают латинской буквой «a», и малая, которую обозначают буквой «b». Тоже латинской.

Большая полуось — это расстояния от центра эллипса до самой дальней его точки. Соответственно, малая полуось — это расстояние от центра до самой ближней точки эллипса.

Эксцентриситет

Еще одна важная характеристика эллипса носит шикарное название — эксцентриситет. Его обычно обозначают буквой «е» и определяют как отношение фокусного расстояния эллипса (c) к большой полуоси (a).

    [e =frac {c}{a}]

Эллипс иногда называют сплющенной окружностью. Так вот эксцентриситет как раз показывает насколько эта окружность сплющена.

Для эллипса:

    [0<e<1]

Чем ближе эксцентриситет к единице, тем более вытянутый эллипс мы получим. И наоборот эксцентриситет близкий к 0, будет иметь эллипс ну очень похожий на окружность. В принципе можно сказать что окружность это эллипс с е=0.

В солнечной системе самый маленький эксцентриситет у Венеры всего 0,007, то есть траектория ее движения это практически окружность. Эксцентриситет близкий к единице имеют кометы. К примеру у кометы Галея е=0,967.

Что же касается Земли, то эксцентриситет земной орбиты тоже очень близок к нулю, всего 0,017. Но тем не менее это не ноль. А это значит что расстояние от Земли до Солнца величина отнюдь не постоянная.

Афелий и перигелий

Точка в которой планета находится ближе всего к Солнцу называется перигелий. От греческого perihelion, “peri“ — рядом и “helios“ — Солнце. Противоположная перигелию точка называется афелий. Соответственно это точка где планета максимально удалена от светила.

Земля находится перигелии, начале января. Она приближается к Солнцу на расстояние в 147,1 миллионов километров. Афелий она проходит в начале июля, когда удаляется на 152,1 миллионов километров. Разница выходит около 5 миллионов километров.

афелий и перигелий

Этим иногда объясняют то что зимы в северном полушарии менее суровые, нежели в южном. Все таки зимой мы чуть ближе к солнцу. С другой стороны так как земля получает меньше солнечной энергии в июле, лето в северном полушарии более прохладное.

Второй закон Кеплера

Итак, мы сказали что согласно первому закону Кеплера Земля движется не по круговой, а по эллиптической орбите. Что же касается ее скорости, то она возрастает при приближении к Солнцу, и убывает при удалении от него.

Кеплер сформулировал это следующим образом:

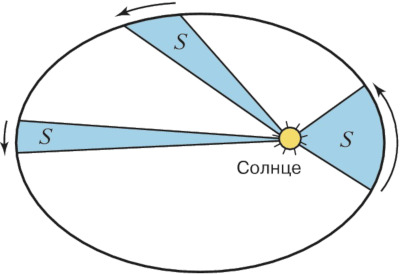
За одинаковые промежутки времени радиус-вектор планеты описывает одинаковые площади.
Второй закон Кеплера

Это так называемый закон площадей или второй закон Кеплера, пожалуй в самой бесполезной его формулировке. Но фактически мы имеем дело с законом сохранения момента импульса. И куда больший интерес для нас будет иметь следующее уравнение:

    [upsilon_1cdot r_1 =upsilon_2cdot r_2]

Произведение линейной скорости и радиус-вектора в перигелии, равно произведению скорости и радиус-вектора афелии. Это частный случай второго закона Кеплера, соответственно для максимального и минимального значений скорости движения планеты.

Максимальная и минимальная скорость движения Земли

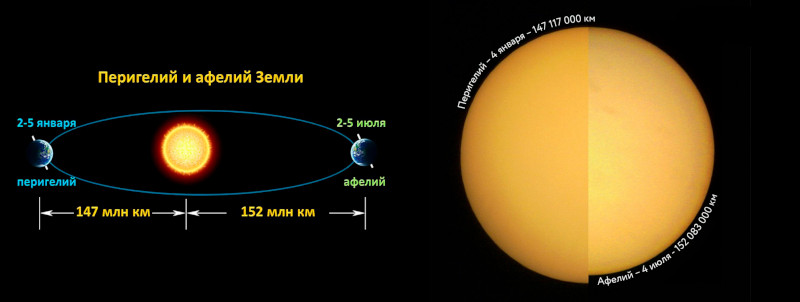
Зная это можно, рассчитать с какими скоростями движется Земля перигелии и афелии. То есть найти ее максимальную и минимальную скорости. Но здесь нам понадобится закон сохранения энергии.

    [frac {mupsilon_1^2}{2} - G frac { M_c cdot m}{r_1} = frac {mupsilon_2^2}{2} - G frac {M_c cdot m}{r_2}]

А так же, формулы для определения расстояний от солнца до афелия и перигелия, через эксцентриситет и большую полуось:

    [r_1 = a(1-e)]

    [r_2 = a(1+e)]

Ну и пожалуй уравнение для нахождения первой космической скорости.

    [upsilon =sqrt{frac {G*M_c}{R}}]

Единственное в формуле расстояние R мы заменим на a, то есть на большую полуось. Большая полуось земной орбиты — это среднее расстояние от Земли до Солнца, и именно значение большой полуоси мы использовали в расчетах в самом начале. А значит скорость которую мы рассчитывали в самом начале есть средняя орбитальная. Она нам пригодится.

    [upsilon =sqrt{frac {G*M_c}{a}}]

Составляем небольшую систему уравнения и с точки зрения физики задача решена. Остается только математика.

    [begin{cases} upsilon_1cdot r_1 =upsilon_2cdot r_2\ frac {mupsilon_1^2}{2} - G frac { M_c cdot m}{r_1} = frac {mupsilon_2^2}{2} - G frac {M_c cdot m}{r_2}\ r_1 = a(1-e)\ r_2 = a(1+e)\ upsilon =sqrt{frac {G*M_c}{a}} end{cases}]

Начнем с того, что сократим массу Земли в законе сохранения энергии, а так же заменим радиус векторы r_1, r_2 на, соответственно, a(1-e), a(1+e).

    [begin{cases} upsilon_1cdot a(1-e) =upsilon_2cdot a(1+e)\ frac {upsilon_1^2}{2} - G frac { M_c}{a(1-e)} = frac {upsilon_2^2}{2} - G frac {M_c}{a(1+e)}\ upsilon =sqrt{frac {G*M_c}{a}} end{cases}]

Если внимательно посмотреть, то можно увидеть что в отношениях G frac { M_c}{a(1-e)}, и G frac {M_c}{a(1+e)}, G frac {M_c}{a}, это квадрат средней орбитальной скорости upsilon ^2. А ее мы уже рассчитали в самом начале. Так что здесь удобно будет выполнить замену.

    [begin{cases} upsilon_1cdot a(1-e) =upsilon_2cdot a(1+e)\ frac {upsilon_1^2}{2} - frac { upsilon ^2}{1-e} = frac {upsilon_2^2}{2} - G frac {upsilon ^2}{1+e}]

Теперь из первого уравнения выражаем upsilon_2, и подставляем это все во второе. Делаем все необходимые преобразования и выражаем upsilon_1:

    [upsilon_1 =upsilon sqrt{frac {1+e}{1-e}}]

Ну и теперь так же выражаем upsilon_2:

    [upsilon_2 =upsilon sqrt{frac {1-e}{1+e}}]

Остается только подставить значения, и посчитать.

upsilon_1 = 29775.559 sqrt{frac {1+0.017}{1-0.017}} approx 30 286,1м/с

upsilon_2 = 29775.559 sqrt{frac {1-0.017}{1+0.017}} approx 29 273,6м/с

Третий закон Кеплера

Опубликовав в 1609 г. два своих закона Иоганн Кеплер так и не остался удовлетворен, и продолжил поиски, которые спустя десять лет привели его к открытию третьего закона.

Квадраты звездных периодов обращений планет относятся между собой как кубы больших полуосей их орбит.

    [frac {T_1^2}{T_2^2}} =frac {a_1^3}{a_2^3}}]

Но это уже совсем другая история…

Источник

Физика, космос, планеты, астрономия, космонавтика. Автор одноименного Дзен канала dzen.ru/…  · 23 мая 2021

Для этого нужно вспомнить формулу линейной скорости при круговом вращении

V = (2*П*R)/T,

где R – радиус, он же расстояние от Земли до Солнца (150 млн. км),

Т – период обращения Земли (1 год).

Затем нужно перевести километры в метры, года в секунды и подставить численные значения. При правильных расчетах должно получиться 30000 м/сек, т.е. 30 км/сек.

2,5 K

средняя скорость движения Земли по орбите вокруг Солнца составляет

29,78 км/с

Комментировать ответ…Комментировать…

Ответы на похожие вопросы

С какой скоростью вращается земля по солнечной орбите? — 2 ответа, задан 23 мая 2021

Космология, физика, военная техника, авиация и ракетостроение. Шахматы слегка, поделки и…  · 8 июл 2021

Земля ВРАЩАЕТСЯ вокруг своей оси со скоростью один оборот в сутки, а ОБРАЩАЕТСЯ вокруг Солнца за один год. При этом поступательная скорость движения Земли по орбите вокруг Солнца составляет около 30 кмсек. В свою очередь Солнце, находясь в одном из трех рукавов Галактики, обращается вокруг ее центра с известной скоростью, увлекая за собой все планеты и другие объекты Солнечной системы, тем самым придавая им соответствующую дополнительную скорость поступательного движения (но это вне рамок заданного вопроса)…

423

Комментировать ответ…Комментировать…

Источник

Как известно, наша планета движется, и не только вокруг Солнца, но и вокруг своей оси. Вдобавок, мы знаем, что для любого движения характерна определённая скорость, которая может зависеть (как и само движение) от различных факторов. Следовательно, вращение Земли также имеет свою скорость.

Земля

Земля

Скорость — это векторная физическая величина, характеризующая быстроту перемещения материальной точки за любой отрезок времени относительно величины промежутка.

Скорость вращения Земли

Правда, земная скорость — вещь относительна. Так как для её расчёта нужна определённая точка отсчёта. Например, для того, чтобы вычислить с какой скоростью движется Земля вокруг своей оси, такой точкой является центр планеты.

Однако, говоря о подобном параметре земельного кружения, важно знать, что скорость разделяют на угловую и линейную.

Угловая скорость

Это величина, которая равна отношению угла тела к отрезку времени, затраченному на этот поворот. Можно сказать, что это быстрота изменения угла тела за промежуток времени. Выражается она в радианах в секунду, и для всех точек имеет постоянное значение.

Как выяснилось, на полный оборот нашей планеты вокруг своей оси требуется 23 часа 56 минут 4,09053 секунды. Проще говоря, одни звездные сутки.

Формула угловой скорости: отношение изменения угла за время.

Формула угловой скорости

Формула угловой скорости

Так как земной оборот равен 360 градусов или 2π (2*3,14=6,28), а время этого оборота в секундах 86344, то угловая скорость вращения Земли вокруг своей оси приблизительно равна 7,26851851851-5с-1.

Линейная скорость

Такую характеристику применяют для того, чтобы выразить темп движения по окружности. Как известно, при круговом вращении тела его разные точки имеют разные скорости. Хотя угловая величина перемещения для них остаётся неизменной.

Формула линейной скорости

Формула линейной скорости

А это значит, что скорость вращения Земли равна примерно 465 м/сек. То есть расчет производится путём деления окружности на время, затраченное на весь оборот.

Однако скорость движения Земли изменяется, потому как её окружность также меняется относительно широты. Ведь радиус планеты уменьшается к полюсам. Соответственно, на разных широтах разный темп вращения. Другими словами, где меньший радиус медленнее и скорость. К примеру, на полюсах она почти нулевая, а на экваторе составляет 1674 км/час.

Для того, чтобы рассчитать скорость вращения Земли на другой широте, необходимо косинус выбранной широты умножить на экваторную скорость. Например, быстроту движения планеты на широте 30 градусов мы вычислим, если косинус 30 градусов, который равен 0,866, умножим на 1674. Таким образом, получаем 1449,7 км/час.

С какой скоростью Земля движется относительно Солнца

Поскольку наша планета, как и другие планеты звездной группы, движутся вокруг Солнца, у данного движение также есть своя скоростная величина.

На полный оборот вокруг главного светила уходит 365 дней 5 часов 48 минут и 46 секунд. Хотя мы привыкли округлять и говорить просто один год. Между прочим за каждый такой год накапливается по пять часов, так сказать, лишних. Но и им нашли место, их объединяют и каждому следующему четвертому году добавляют один день. Наверняка вы догадались, что такие года называются високосными.

Вращение Земли вокруг Солнца

Вращение Земли вокруг Солнца

На основании данных о времени полного оборота планеты вокруг Солнца, не трудно вычислить с какой быстротой она движется относительно него. Следует учитывать, что двигаемся мы по орбите. А значит определяем с какой скоростью Земля летит именно по орбите.

Как рассчитать темп земного движения вокруг Солнца

Для этого необходимо радиус орбиты или расстояние до Солнца (≈150 млн км) умножить на 2π (23,14=6,28), что составляет 942 млн км. Все это разделим на время, затраченное на этот промежуток (365 дней 24 часа*3600 секунд=31 536 000 секунд). В итоге получаем 29,87 км в секунду.

Принято считать, что средняя скорость Земли по орбите (по окружности Солнца) равна 30 км/сек.

По данным учёных, скорость вращения Земли вокруг своей оси постепенно уменьшается. Причем наблюдаются пятилетние циклы то ускорения, то замедления движения планеты. Но объяснить по какой причине происходят такие изменения пока не получается. Поэтому за движением нашей планеты ведётся постоянное наблюдение и мониторинг. Возможно, отыщется какая-либо взаимосвязь данного явления.

Источник

Как можно вычислить скорость движения Земли вокруг Солнца?

Александра Шилова



Ученик

(82),
закрыт



9 лет назад

Дополнен 9 лет назад

Вот есть формула: скорость движения тела = путь пройденный телом разделить на время движения тела.

Дополнен 9 лет назад

Еще есть несколько формул…. Или l или t =2п=пd….и l=150000000 км. ну путь пройденый телом это понятно…. что такое п и пd?

Трудное детство

Оракул

(70151)


9 лет назад

среднюю скорость из равенства сил, тяготения и центробежной. mV^2/R=GMm/R^2. отсюда V=(GM/R)^1/2, где M масса солнца, а R – средний радиус земной орбиты. для нахождения мгновенной скорости надо использовать 2 закон кеплера.

daybit

Высший разум

(146228)


9 лет назад

Длина орбиты Земли равна 2*pi*R, где pi = 3.14, а радиус орбиты R = 150 млн км. Итого длина орбиты = 942 000 000 км.

В году 365.25 дней, в сутках 24 часа, в 1 часе 3600 секунд, все перемножаем и получаем 365,25*24*3600 = 31 557 600 сек.

Делим 942 000 000 км на 31 557 600 сек, получаем 29.85 км/сек

Источник

$begingroup$

I know that there are several formulae that one can plug numbers into to arrive an estimate of Earth’s speed around the sun (Kepler’s third law for instance), but I’m wondering how these things are measured.

Since Earth is moving in an ellipse around the Sun, I thought doppler measurements of spectral lines would help tell where we were on the ellipse, since the velocity won’t be constant everywhere.

But other than that, I’m not sure how one measures Earth’s velocity.

Waffle's Crazy Peanut's user avatar

asked Dec 31, 2012 at 12:39

Kitchi's user avatar

$endgroup$

0

$begingroup$

There is a lovely presentation by Terence Tao of UCLA, The Cosmic Distance Ladder, that explains this, and much, much more, in detail. Here’s a youtube of it, and here are the slides he used.

As a brief summary, to measure Earth’s velocity, you need to know the distance to the Sun, plus its orbital period of 1 year. The earliest method to do so is due to Aristarchus, and was based on the half moon not happening exactly midway between the full and new moons. It required knowing the Earth-Moon distance, which required knowing the Moon size, which required knowing the Earth size, hence the distance ladder.

I won’t spoil the fun of reading/watching it by trying to reproduce any more of it here.

answered Dec 31, 2012 at 13:22

Jaime's user avatar

JaimeJaime

3,89818 silver badges24 bronze badges

$endgroup$

2

$begingroup$

The orbital velocity of the Earth can be measured via the annual Doppler effect, or by aberration. The Doppler effect measurement requires a star near the ecliptic, and the aberration measurement requires a star normal to it. Both techniques involve comparing two observations taken six months apart.

For example the aberration constant is 20.496 arcseconds, or .000099365 radians. Multiplying the aberration constant in radians by the speed of light gives the mean orbital velocity of the Earth-Moon barycenter: $ .000099365 , c = 29.79 mathrm{km}/mathrm s $.

The annual Doppler effect must be removed from all spectroscopic radial velocity measurements in order to find the radial velocity of the observed star with respect to the solar system barycenter.

answered Jul 26, 2013 at 18:20

Nick's user avatar

NickNick

1,59212 silver badges25 bronze badges

$endgroup$

Источник

Добавить комментарий