Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.
Кинематические характеристики движения
Важные факты!
Графически движение горизонтально брошенного тела описывается следующим образом:
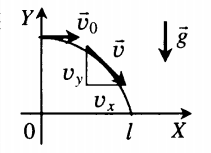
- Вектор скорости горизонтально брошенного тела направлен по касательной к траектории его движения.
- Проекция начальной скорости на ось ОХ равна v0: vox = v0. Ее проекция на ось ОУ равна нулю: voy = 0.
- Проекция мгновенной скорости на ось ОХ равна v0: vx = v0. Ее проекция на ось ОУ равна нулю: vy = –gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
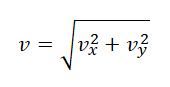
Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:
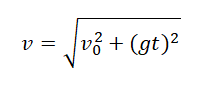
Минимальная скорость в течение всего времени движения равна начальной скорости: vmin = v0.
Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: vmax = v.
Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:
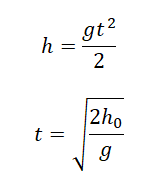
h0 — высота, с которой тело бросили в горизонтальном направлении.
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0tпад
Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид:
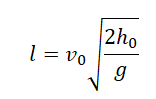
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
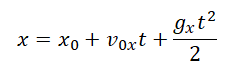
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:
x = v0t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
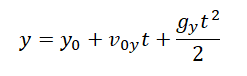
Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?
Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:
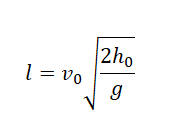
Выразим начальную скорость и вычислим ее:
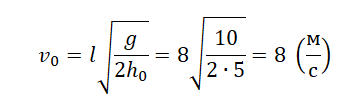
Горизонтальный бросок тела с горы
Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.
График горизонтального броска тела с горы
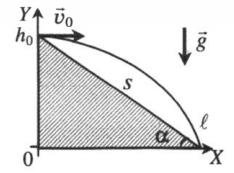
α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения
Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:
l = s • cosα
Начальная высота — высота, с которой было брошено тело. Обозначается h0. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:
h0 = s sinα
Пример №2. На горе с углом наклона 30о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?
Выразим это расстояние через дальность полета:
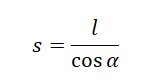
Дальность полета выражается по формуле:
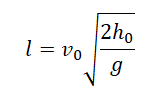
Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:
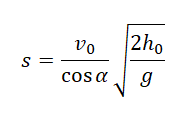
Выразим с учетом формулы начальной высоты:
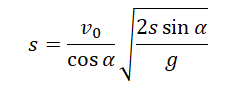
Преобразуем:
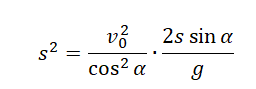
Поделим обе части выражения на общий множитель s:
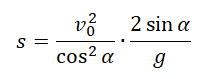
Подставим известные значения:
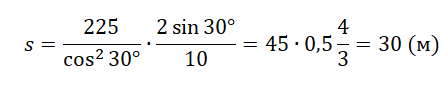
Задание EF18083
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
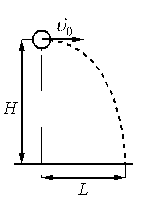
В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2υ0.
Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости и массы.
- Определить характер изменения физической величины при увеличении начальной скорости и массы шарика.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
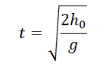
Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
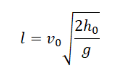
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 313.
Ответ: 313
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18048
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
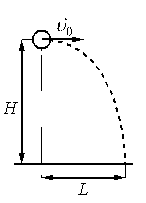
Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости.
- Определить характер изменения физической величины при уменьшении начальной скорости.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
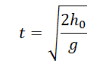
Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
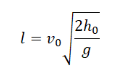
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 323.
Ответ: 323
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 18.2k
Движение горизонтально брошенного тела:
Рассмотрим движение шара, движущегося прямолинейно по поверхности стола с высотой 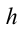
При достаточно малом сопротивлении воздуха, которым можно пренебречь, тело будет двигаться в горизонтальном направлении равномерно со скоростью 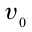 . Поэтому перемещение
. Поэтому перемещение
в горизонтальном направлении в любой момент времени 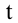 , или длина полета, определяется следующей формулой:
, или длина полета, определяется следующей формулой:

Проекции скорости тела на оси 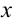 и
и 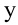 определятся следующими соотношениями:
определятся следующими соотношениями:

В вертикальном же направлении, двигаясь равноускоренно без начальной скорости, тело будет свободно падать с высоты 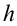 . Следовательно, положение тела в вертикальном направлении после произвольного времени
. Следовательно, положение тела в вертикальном направлении после произвольного времени 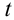 будет определяться формулой:
будет определяться формулой:

Из соотношений (1.21) и (1.22) уравнение траектории движения горизонтально брошенного тела на плоскости 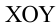 будет иметь следующий вид:
будет иметь следующий вид:

Выражение (1.24) является уравнением параболы. Значит, горизонтально брошенное тело будет двигаться по параболической линии. Время полета тела, брошенного горизонтально с высоты 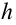 , определяется выражением:
, определяется выражением:

В этом случае формула для расчета длины полета тела будет иметь вид:

Горизонтально брошенное тело, одновременно двигаясь в горизонтальном направлении равномерно и в вертикальном направлении равноускоренно, свободно падает. К концу движения (после истечения времени 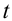 ) скорости в горизонтальном и вертикальном направлении будут
) скорости в горизонтальном и вертикальном направлении будут 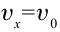 и
и 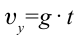 соответственно. Таким образом, скорость тела при падении на землю определяется выражением:
соответственно. Таким образом, скорость тела при падении на землю определяется выражением:
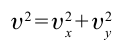
или

Перемещение и траектория тела при криволинейном движении неравны между собой. Модуль вектора и направление движения горизонтально брошенного тела на протяжении движения меняются непрерывно.
Образец решения задачи:
Тело брошено горизонтально на высоте 35 м со скоростью 30м/с. Найти скорость тела при падении на землю.
Дано:
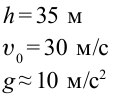
Найти:
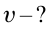
Формула:
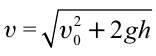
Решение:
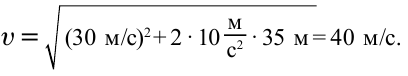
Ответ: 40 м/c.
Движение тела, брошенного горизонтально и под углом к горизонту
Если материальная точка участвует одновременно в нескольких движениях, то такое движение называют сложным.
Примером сложного движения является движение под действием силы тяжести в том случае, если падающему телу сообщена начальная скорость, непараллельная вектору ускорения свободного падения.
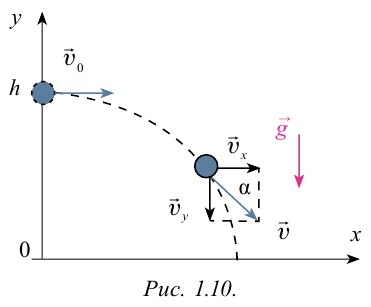
Рассмотрим движение тела, брошенного горизонтально со скоростью 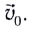 Выберем систему координат так, что ее начало находится на поверхности Земли, направив ось Ох горизонтально, а ось Оу — вертикально (рис. 23).
Выберем систему координат так, что ее начало находится на поверхности Земли, направив ось Ох горизонтально, а ось Оу — вертикально (рис. 23).
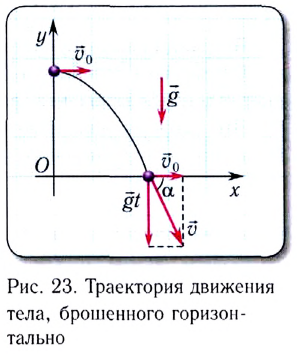
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного с постоянной скоростью 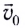 вдоль горизонта (оси Ох) и свободного падения в вертикальном направлении с ускорением
вдоль горизонта (оси Ох) и свободного падения в вертикальном направлении с ускорением 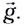
Движение тела в горизонтальном направлении будет описываться уравнением

а в вертикальном — уравнением

Здесь 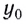 — координата тела по оси Оу в начальный момент времени
— координата тела по оси Оу в начальный момент времени 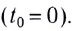 Если тело брошено с высоты
Если тело брошено с высоты 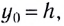 то время падения
то время падения 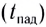 определяется из
определяется из
условия 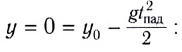
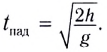
Для получения уравнения траектории движения у(х) необходимо исключить время из уравнений движения (1) и (2). Из уравнения (1) выражаем время t и подставляем в уравнение (2). Получаем 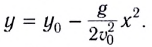
Это уравнение параболы, ветви которой направлены вниз, так как коэффициент перед множителем 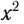 отрицательный.
отрицательный.
Скорость вдоль направления оси Ох остается неизменной и равной 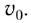
Вдоль оси Оу движение равноускоренное. В начальный момент времени вертикальная составляющая скорости равна нулю 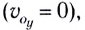 поэтому мгновенная скорость вдоль оси Оу находится из соотношения
поэтому мгновенная скорость вдоль оси Оу находится из соотношения 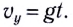 Модуль мгновенной скорости определяется по теореме Пифагора (см. рис. 23):
Модуль мгновенной скорости определяется по теореме Пифагора (см. рис. 23):
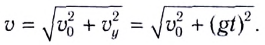
Угол между начальной скоростью 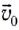 и мгновенной скоростью и в момент времени t можно найти из соотношения
и мгновенной скоростью и в момент времени t можно найти из соотношения
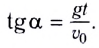
В приведенных формулах сопротивление воздуха не учитывается.
Рассмотрим теперь движение тела, брошенного со скоростью 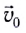 под некоторым углом
под некоторым углом 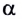 к горизонту (рис. 24).
к горизонту (рис. 24).
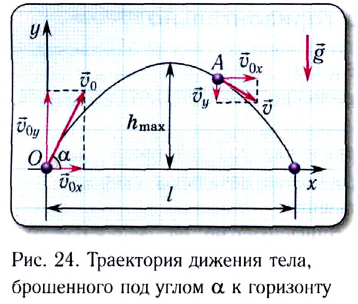
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного в горизонтальном направлении со скоростью 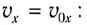

и равноускоренного в вертикальном направлении с ускорением 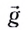 и начальной
и начальной
скоростью 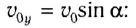

В том случае, если система координат выбрана так, что начальные координаты 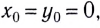 уравнение траектории движения имеет вид
уравнение траектории движения имеет вид

Как и при движении тела, брошенного горизонтально, траектория представляет собой параболу, ветви которой направлены вниз, поскольку коэффициент перед 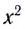 отрицателен. Вершина параболы при этом имеет координаты
отрицателен. Вершина параболы при этом имеет координаты 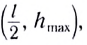
где l — дальность полета тела, 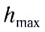 — максимальная высота его подъема в процессе полета.
— максимальная высота его подъема в процессе полета.
Модули горизонтальной 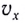 и вертикальной
и вертикальной 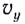 составляющих мгновенной скорости
составляющих мгновенной скорости 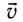 движения определяются из следующих соотношений:
движения определяются из следующих соотношений:

Мгновенную скорость 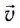 и движения тела в произвольной точке Л траектории можно найти как векторную сумму горизонтальной
и движения тела в произвольной точке Л траектории можно найти как векторную сумму горизонтальной 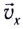 и вертикальной
и вертикальной 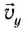 мгновенных скоростей движения (см. рис. 24).
мгновенных скоростей движения (см. рис. 24).
Время подъема тела можно найти из условия 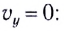
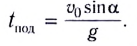
Если сопротивление воздуха при движении не учитывается, то время подъема равно времени падения: 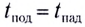 (докажите это самостоятельно).
(докажите это самостоятельно).
Таким образом, время полета тела можно найти как
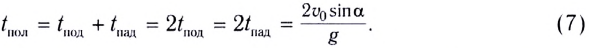
Определив вертикальную составляющую скорости 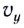 в искомый момент времeни, по формуле
в искомый момент времeни, по формуле 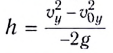 можно найти высоту, на которой находится тело.
можно найти высоту, на которой находится тело.
Максимальная высота подъема тела 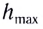 легко определяется из условия, что вертикальная составляющая скорости в этой точке равна пулю
легко определяется из условия, что вертикальная составляющая скорости в этой точке равна пулю 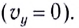 Тогда
Тогда

Дальность полета l — расстояние, пройденное телом за время полета 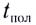 вдоль оси Ох с постоянной скоростью
вдоль оси Ох с постоянной скоростью 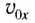 (см. рис. 24). Она определяется по формуле
(см. рис. 24). Она определяется по формуле
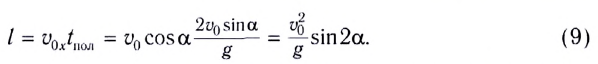
Таким образом, дальность полета определяется модулем начальной скорости 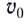 тела и углом его бросания
тела и углом его бросания 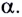
Заметим, что согласно формуле (9) при неизменном модуле начальной скорости тела максимальная дальность 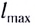 полета достигается при
полета достигается при 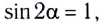 т. е. при угле бросания
т. е. при угле бросания 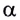 = 45°.
= 45°.
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея
- Движение в гравитационном поле
- Зависимость веса тела от вида движения
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Взаимная передача вращательного и поступательного движения
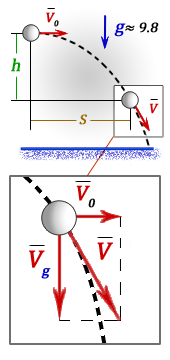
h – высота на которую опустилось тело за время t
S – расстояние по горизонтали, пройденное телом за время t
V – скорость тела, направленная по касательной к траектории движения, через время t
Vo – начальная скорость тела, которая является составляющей скорости V и направленна по горизонтали (не меняется со временем)
Vg – составляющая скорости V, направленная по вертикали вниз, возникает под воздействием силы тяжести и в начале броска равна нулю
t – время падения тела на высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
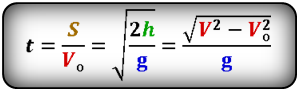
Используя теорему Пифагора, по формуле, находим численное значение скорости V, а по правилу сложения векторов, можем определить направление , которое всегда будет по касательной к траектории движения :
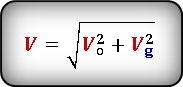
Формула скорости тела в момент времени t (V):
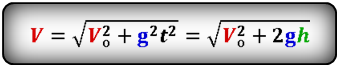
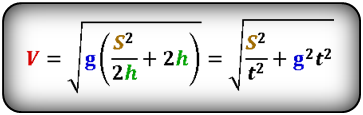
Формула начальной скорости тела (Vo):
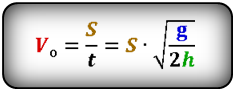
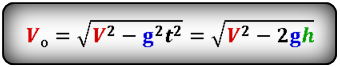
Формула расстояния по горизонтали, которое пролетело тело при падении (S):

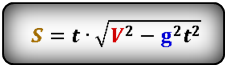
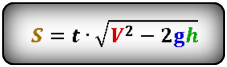
Формула высоты, на которую опустилось тело при падении (h):
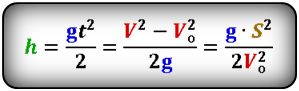
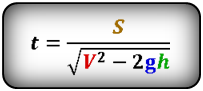
Формула времени падения тела (t):
- Подробности
-
Опубликовано: 11 августа 2015
-
Обновлено: 13 августа 2021
Движение тела брошенного горизонтально, теория и онлайн калькуляторы
Движение тела брошенного горизонтально
Постановка задачи. Начальные условия
Рассмотрим движение тела, которое бросили с начальной скоростью ${overline{v}}_0 $параллельно Земле (горизонтально) рис.1. с некоторой высоты $h_0.$
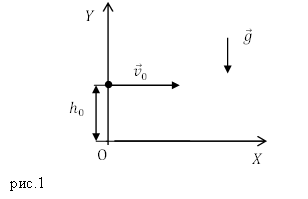
Систему отсчета свяжем с Землей. Ось X направим параллельно Земле, ось Y перпендикулярно оси X, вверх. Тело движется под воздействием силы тяжести, если не учитывать силу трения, то другие силы на тело не действуют. Движение тела происходит в плоскости, в которой лежат векторы: начальной скорости тела ${overline{v}}_0$ и ускорения $overline{g}. $
Начальные условия при рассматриваемом нами движении точки:
[при t=0 cleft{ begin{array}{c}
x_0=0, \
y_0=h_0, \
v_{0x}=v_0, \
v_{0y}=0 end{array}
right.left(1right).]
Вектор ускорения при движении под действием силы тяжести считают постоянным:
[overline{a}=overline{g}left(2right),]
так как textit{ }$overline{g}$ направлен вертикально вниз, то:
[left{ begin{array}{c}
a_x=0, \
a_y=g end{array}
right.left(3right).]
где $gapprox $ 9,8 $frac{м}{с^2}.$
Кинематические уравнения движения тела брошенного горизонтально
Кинематическое уравнение для скорости равнопеременного движения в поле тяжести имеет вид:
[overline{v}left(tright)={overline{v}}_0+overline{g}t left(4right),]
где ${overline{v}}_0$ – начальная скорость тела. Движение материальной точки в рассматриваемом случае можно представить сумму двух независимых движений по прямым линиям, в которых участвует тело, брошенное горизонтально. Это равномерное движение с неизменной скоростью ${overline{v}}_0$ в горизонтальном направлении и равноускоренное движение с ускорением $overline{g}$ без начальной скорости в направлении вектора ускорения свободного падения.
В проекциях на оси координат получаем:
[left{ begin{array}{c}
v_x=v_0 \
v_y=-gt end{array}
left(5right).right.]
Модуль скорости движения точки при этом равен:
[v=sqrt{v^2_x+v^2_y}=sqrt{v^2_0+g^2t^2}left(6right).]
Уравнение для перемещения тела, брошенного горизонтально, запишем как:
[overline{s}left(tright)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}(7),]
где ${overline{s}}_0$ – смещение тела в начальный момент времени. В нашем случае $s_0=y_0=h_0$. Векторное уравнение (7) даст два скалярных выражения для координат падающей точки:
[left{ begin{array}{c}
x=v_0t \
y{=h}_0-frac{gt^2}{2} end{array}
left(8right).right.]
Ка уже говорилось, каждое из двух отдельных движений тела происходит по прямой, но траекторией движения падающего тела является ветвь параболы, находящаяся в плоскости в которой лежат ${overline{v}}_0$ и $overline{g}$.
Из системы уравнений (8) легко получить уравнение траектории движения точки, исключая из уравнений время:
[t=frac{x}{v_0};; y{=h}_0-frac{g{left(frac{x}{v_0}right)}^2}{2}to y=h_0-frac{gx^2}{{2v}^2_0}left(9right).]
Высшей точкой траектории движения тела в нашем случае является точка бросания.
Время полета тела брошенного горизонтально, дальность полета
Время полета тела просто найти из второго уравнения системы (8), если положить, что в момент падения координата точки $y=0$:
[y{=h}_0-frac{g{t_{pol}}^2}{2}=0to h_0=frac{g{t_{pol}}^2}{2}to t_{pol}=sqrt{frac{2h_0}{g}}left(10right).]
Дальность полета (s) – это расстояние, которое тело преодолело по горизонтали (по оси X). Его найдем, подставив время полета в первое уравнение системы (8):
[s=v_0sqrt{frac{2h_0}{g}} left(11right).]
Примеры задач с решением
Пример 1
Задание. Маленький шарик бросили горизонтально со скоростью $v_0$. Какова высота, с которой бросили шарик, если он упал на землю, пролетев расстояние s по горизонтали в n раз большее, чем высота бросания?
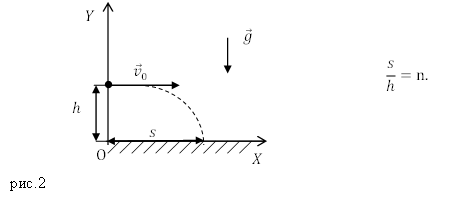
Решение. Для решения задачи воспользуемся формулой, которую получили в теоретической части статьи, связывающую дальность полета тела и высоту, с которой это тело бросили горизонтально:
[s=v_0sqrt{frac{2h}{g}} left(1.1right).]
Воспользуемся условием, которое задано:
[frac{s}{h}{rm =n}to s=nh left(1.2right).]
Выразим из формулы (1.1) искомую высоту, приняв во внимание (1.2), имеем:
[nh=v_0sqrt{frac{2h}{g}}to n^2h^2=v^2_0frac{2h}{g}to h=frac{2v^2_0}{gn^2}.]
Ответ. $h=frac{2v^2_0}{gn^2}$
Пример 2
Задание. Напишите уравнения траектории движения материальной точки М для случая, который изображен на рис. 3.
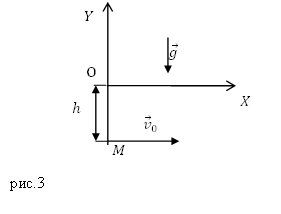
Решение. Основой решения задачи служит кинематическое уравнение для перемещения при равноускоренном движении:
[overline{s}left(tright)={overline{s}}_0+{overline{v}}_0t+frac{overline{a}t^2}{2}left(2.1right).]
Спроектируем выражение (2.1) на оси X и Y:
[left{ begin{array}{c}
x=v_0t, \
y=-h-frac{gt^2}{2} end{array}
left(2.2right).right.]
Для того чтобы получить уравнение траектории выразим время из первого уравнения системы (2.2):
[t=frac{x}{v_0} left(2.3right).]
Подставим найденное время (2.3) во второе уравнение системы (2.3):
[y=-h-frac{g}{2}frac{x^2}{{v_0}^2}.]
Ответ. $y=-h-frac{g}{2}frac{x^2}{{v_0}^2}$
Читать дальше: движение тела под углом к горизонту.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
2010-03-24 22:32
Рассмотрим движение тела, брошенного горизонтально и движущегося под действием одной только силы тяжести (сопротивлением воздуха пренебрегаем). Например, представим себе, что шару, лежащему на столе, сообщают толчок, и он докатывается до края стола и начинает свободно падать, имея начальную скорость
![]()
, направленную горизонтально (рис. 174).
Спроектируем движение шара на вертикальную ось
![]()
и на горизонтальную ось
![]()
. Движение проекции шара на ось
![]()
— это движение без ускорения со скоростью
![]()
; движение проекции шара на ось
![]()
— это свободное падение с ускорением
![]()
бее начальной скорости под действием силы тяжести. Законы обоих движений нам известны. Компонента скорости
![]()
остается постоянной и равной
![]()
. Компонента
![]()
растет пропорционально времени:
![]()
. Результирующую скорость легко найти по правилу параллелограмма, как показано на рис. 175. Она будет наклонена вниз, и ее наклон будет расти с течением времени.
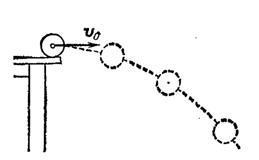
Рис. 174. Движение шара, скатившегося со стола
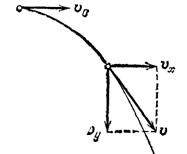
Рис. 175. Шар, брошенный горизонтально со скоростью ![]()
имеет в момент
![]()
скорость
![]()
Найдем траекторию тела, брошенного горизонтально. Координаты тела в момент времени
![]()
имеют значения
![]()
, (112.1)
![]()
(112.2)
Чтобы найти уравнение траектории, выразим из (112.1) время
![]()
через
![]()
и подставим это выражение в (112.2). В результатё получим
![]()
(112.3)
График этой функции показан на рис. 176. Ординаты точек траектории оказываются пропорциональными квадратам абсцисс. Мы знаем, что такие кривые называются параболами. Параболой изображался график пути равноускоренного движения (§ 22). Таким образом, свободно падающее тело, начальная скорость которого горизонтальна, движется по параболе.
Путь, проходимый в вертикальном направлении, не зависит от начальной скорости. Но путь, проходимый в горизонтальном направлении пропорционален начальной скорости. Поэтому при большой горизонтальной начальной скорости парабола, по которой падает тело, более вытянута в горизонтальном направлении. Если из расположенной горизонтально трубки выпускать струю воды (рис. 177), то отдельные частицы воды будут, так же как и шарик, двигаться по параболе. Чем больше открыт кран, через который поступает вода в трубку, тем больше начальная скорость воды и тем дальше от крана попадает струя на дно кюветы. Поставив позади струи экран с заранее начерченными на нем параболами, можно убедиться, что струя воды действительно имеет форму параболы.

Рис. 176. Траектория тела, брошенного горизонтально

Рис. 177. Струя имеет форму параболы, тем более вытянутой, чем больше начальная скорость воды
Зная начальную скорость
![]()
и высоту падения
![]()
, можно найти расстояние
![]()
по горизонтали до места падения. Действительно, положив в формуле (112.3)
![]()
и
![]()
, получим
![]()
.
112.1.
Какова будет через 2с полета скорость тела, брошенного горизонтально со скоростью 15м/с? В какой момент скорость будет направлена под углом 45° к горизонту? Сопротивлением воздуха пренебречь.
112.2.
Шарик, скатившийся со стола высоты 1м, упал на расстоянии 2м от края стола. Какова была горизонтальная скорость шарика? Сопротивлением воздуха пренебречь.
