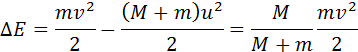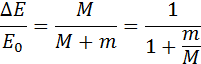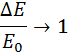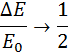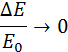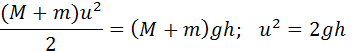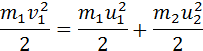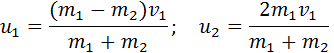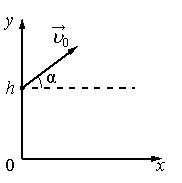Как определить скорость тела в момент удара о землю?
Ученик
(231),
на голосовании
8 лет назад
Голосование за лучший ответ
Александра Левина
Профи
(990)
8 лет назад
по закону сохранения энергии Е1=Е2
Е1-мех. энергия тела, когда оно начало падать
Е2-мех. энергия тело в момент удара о землю
Е1=К1+П1 ( в этот момент К1=0, т. к. когда тело начало падать, его скорость равна 0)
П1=mgh
E1=mgh
Е2=К2+П2 (в этот момент П2=0, т. к. высота равна 0)
К2=mv^2/2
E2=mv^2/2
т. к. Е1=Е2 то mgh=mv^2/2
сократим на m: gh=v^2/2
h=v^2/2g= 100^2/2*10=500 м
2.1
Расчет скорости шарика до удара.
Формула
:
1=2*Sin(
i
/
2)*g*L
L
– Длинна
нити.
g
– Скорость свободного падения.
1
–
Скорость
шарика до удара.
I
– Угол
отклонения шарика.
2.2
Расчет скорости шарика после удара.
Формула
:
2=2*Sin(<
i>
/
2)*g*L
<i>
– Среднее
значение угла отскока шарика.
Производим
вычисления :
1
= 2*Sin(200/2)*9,81*0,315
= 0,605 (м/с).
2= 2*Sin(17.50/2)*
9,81*0,315
= 0,532 (м/с).
1
= 2*Sin(300/2)*9,81*0,315
= 0,905 (м/с).
2
= 2*Sin(26.50/2)*9,81*0,315
= 0,802 (м/с).
1
= 2*Sin(400/2)*9,81*0,315
= 1,197 (м/с).
2
= 2*Sin(35.50/2)*9,81*0,315
= 1,067 (м/с).
1= 2*Sin(500/2)*
9,81*0,315
= 1,479 (м/с).
2
= 2*Sin(430/2)*9,81*0,315
= 1,282 (м/с).
1
= 2*Sin(600/2)*9,81*0,315
= 1,757 (м/с).
2
= 2*Sin(500/2)*9,81*0,315
= 1,479 (м/с).
Результаты расчетов
сведем в таблицу
Таблица
5
|
|
|
|
|
|
|
|
|
0,605 |
0,905 |
1,197 |
1,479 |
1,757 |
|
|
0,532 |
0,802 |
1,067 |
1,282 |
1,479 |
3. Расчет среднего значения силы удара
Формула
:
<
F >
=
<F>
– Среднее
значение силы удара.
m – Масса
шарика.
1
–
скорость
шарика до удара.
2
– скорость
шарика после удара.
–время удара.
Производим
вычисления :
<F1>
= 0,0195*(0,605-0,532)
/
0,0000309 = 46,06 H.
<F2>
= 0,0195*(0,905-0,802)
/ 0,0000287 = 69,98 H.
<F3>
= 0,0195*(1,197-1,067)
/ 0,0000269 = 94,23 H.
<F4>
= 0,0195*(1,479-1,282)
/ 0,0000217 = 177,02 H.
<F5>
= 0,0195*(1,757-1,479)
/ 0,0000191 = 283,82 H.
4. Расчет коэффициента восстановления.
Формула
:
ε
=
2
/
1
ε
– коэффициент восстановления.
ε
1 = 0,532 / 0,605
= 0,878 ε
5 = 1,479 / 1,757
= 1,187
ε
2 = 0,802 / 0,905
= 0,886
ε
3 = 1,067
/ 1,197 = 0,891
ε
4 = 1,282 / 1,479
= 0,866
5.Расчет погрешностей прямых измерений.
5.1
Определяем стандартную погрешность
измерения угла отскока шарика.
Формула
:
SI
=
(
S/I
)2
+
(
S//2
)2.
SI
– среднеквадратичное
отклонение.
S/I
– стандартная
случайная погрешность.
S//2
= 0, 5 – стандартная
систематическая погрешность.
S/I
=
∑(
I
–
<i>)2
/
N
( N
– 1 )
N=10
количество
измерений угла.
S/1=
(180-17.50)2+(17.50-17.50)2+(170-17.50)2+(180-17.50)2+(18.50-17.50)2+(170-17.50
)2
+(17.50-17.50)2+(170-17.50)2+(180-17.50)2+(180-17.50)2
/ 10( 10-1) = 0,176;
S=
(0,
5)2+(0,176)2
= 0,530;
S/2=
(270-26.50)2+(27.50+26.50)2+(260-26.50)2+(26.50-26.50)2+(270-26.50)2+(
270-26.50)2+(26.50-26.50)2+(
270-26.50)2+(
26.50-26.50)2+(
26.50-26.50)2
/ 10( 10-1) = 0,148;
S=
(0,
5)2+(0,148)2
= 0,521;
S/3=
(350-35.50)2+(35.50-35.50)2+(35.50-35.50)2+(360-35.50)2+(
35.50-35.50)2+(35.50-35.50)2+(
350-35.50)2+
(350-35.50)2+(
350-35.50)2+(
35.50-35.50)2
/ 10( 10-1) = 0,104
S=
(0,
5)2+(0,104)2
= 0,510;
S/4=
(43-43)2+(43-43)2+(43.5-43)2+(42-43)2+
(43-43)2+(
43.5-43)2+(
42.5-43)2+
(43-43)+ (43-43)2
+( 42.5-43) / 10( 10-1) = 0,139
S=
(0,
5)2+(0,139)2
= 0,518;
S/5=
(500-500)2+(500.5-500)2+
(500-500)2+(50.50-500)2+
(50.50-500)2+
(50.50-500)2+
(510-500)2+
(500-500)2+(49.50-500)2+
(50.50-500)2
/ 10( 10-1) = 0,158;
S=
(0,
5)2+(0,158)2
= 0,524
5.2
Расчет абсолютной погрешности угла
отклонения шарика
∆i
Формула
:
∆i
=
(kn
*
S/i)2+(1/3*k*S//
2
)2
kn
= 2.3 – соответствующий
коэффициент Стьюдента;
k
=
2.0
– соответствующий
коэффициент Стьюдента;
Производим
вычисления :
∆1=
(2.3*0,176)2+
(1/3*2.0*0, 5)2=
0,524
∆2=
(2.3*0,148)2+
(1/3*2.0*0, 5)2=
0,476
∆3=
(2.3*0,104)2+
(1/3*2.0*0, 5)2=
0,410
∆4=
(2.3*0,139)2+
(1/3*2.0*0, 5)2=
0,461
∆5=
(2.3*0,158)2+
(1/3*2.0*0, 5)2=
0,493
5.2
Определяем относительную погрешность
измерения угла отскока шарика.
Формула
:
εi=
∆I
/
<i>
ε1
=
0,524
/
17,50
= 0,029;
ε2
=
0,476
/
26,50
= 0,016;
ε3
=
0,410
/
35,50
= 0,012;
ε4
= 0,461
/ 43,00
= 0,011;
ε5
= 0,493
/ 50,00
=
0,010;
5.3
Определяем относительную и абсолютную
погрешность измерения угла отклонения
шарика .
Формулы
:
∆i
=
(kn
*
S/i)2+(1/3*k*S//
2
)2
ε
i=
∆I
/
<i>
т.к.
(kn
*
S/i)2
=
0
, то
∆i
=
(1/3*k*S//
2
)2.
Производим
вычисления :
∆I
=(1/3*2.0*0.5)2
= 0,33
ε1
=
0,33/20
= 0,016;
ε2
=
0,33/30
= 0,011;
ε3
=
0,33/40
= 0,008;
ε4
=
0,33/50
= 0,007;
ε5
=
0,33/60 = 0,006;
5.4
Рассчитаем относительную погрешность
измерения времени соударения шарика.
Формула
:
SI
=
∑(
i–
<i>)2
/
N ( N – 1 )
Производим
вычисления
:
S1=10-7*
(321-309)2+(312-309)2+(304-309)2+(312-309)2+(303-309)2+(307-309)2+(315-309)2+(309-309)2+(302-309)2+(311+309)2
/ 10( 10-1) =1,8*10-7
S2=10-7*
(272-287)2+(288-287)2+(271-287)2+(297-287)2+(287-287)2+(301-279)2+(286-287)2
+(291-287)2+(300-287)2
+(279-287)2
/ 10( 10-1) =3,37*10-7
S3=10-7*
(262-269)2+(267-269)2+(269-269)2+(262-269)2+(258-269)2+(252-269)2+(261-269)2
+(243-269)2+(255-269)2+
(261-269)2
/ 10( 10-1) = 4,10*10-7
S4=10-7*
(217+217)2+(216-217)2+(208-217)2+(212-217)2+(206-217)2+(231-217)2+(214-
-217)2+
(227-217)2+(221-217)2+(211-217)2
/ 10( 10-1) = 2,71*10-7
S5=10-7*
(
191-191)2+(189-191)2+(192-191)2+(184-191)2+(190-191)2+(183-191)2+(202-
191)2+
(193-191)2+(201-191)2+(186-191)2
/ 10( 10-1) = 2,27*10-7
5.5
Определим абсолютную погрешность
измерения времени соударения шарика.
Формула
:
∆I
=
(kn*S
)2+(1/3*k*
S/)2
S
–
стандартная
случайная погрешность.
S/
=1*10-7
–
стандартная
систематическая погрешность.
Производим
вычисления :
∆1
=
10-7*(2,3*1,8)2+(1/3*2,0*1)2
= 4,14*10-7;
∆2
=
10-7*(2,3*3,37)2+(1/3*2,0*1)2
= 7,75*10-7;
∆3
=
10-7*(2,3*4,10)2+(1/3*2,0*1)2
= 9,43*10-7;
∆4
=
10-7*(2,3*2,71)2+(1/3*2,0*1)2
= 6,23*10-7;
∆5
=
10-7*(2,3*2,27)2+(1/3*2,0*1)2
= 2,28*10-7;
5.6
Определим относительную погрешность
измерения времени соударения шарика.
Формула
:
ε=
∆I
/
<i>
ε1=
4,
14*10-7
/ 309 * 10-7
= 0,013;
ε2=
7,
75*10-7
/ 287* 10-7
= 0,027;
ε3=
9,
43*10-7
/ 269 *10-7
= 0,035;
ε4=
6,
23*10-7
/ 217* 10-7
= 0,028;
ε5=
2,
28*10-7
/ 191* 10-7
= 0,012;
Соседние файлы в папке Отчёты 1 семестр
- #
- #
28.03.2015126.98 Кб46маятник максвела(1).doc
- #
- #
- #
28.03.2015560.13 Кб43Мех. удар(1).doc
- #
- #
- #
28.03.2015891.39 Кб42Мех.удар(1).doc
- #
- #
- #
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
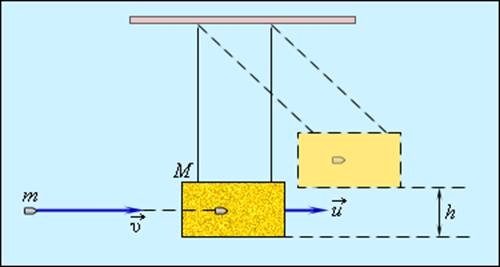
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
Обозначим скорость ящика с застрявшей в нем пулей через Тогда по закону сохранения импульса
При застревании пули в песке произошла потеря механической энергии:
Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.
При m << M
почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M
во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение
Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
где h – максимальная высота подъема маятника. Из этих соотношений следует:
Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.
|
|
|
Рисунок 1.21.1. Баллистический маятник |
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
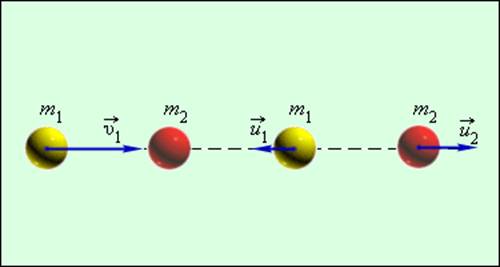
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
|
|
|
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров |
В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u1 и u2 шаров после столкновения:
В частном случае, когда оба шара имеют одинаковые массы (m1 = m2), первый шар после соударения останавливается (u1 = 0), а второй движется со скоростью u2 = υ1, т. е. шары обмениваются скоростями (и, следовательно, импульсами).
Если бы до соударения второй шар также имел ненулевую скорость (υ2 ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ2 относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ1‘ = υ1 – υ2. Определив по приведенным выше формулам скорости u1 и u2 шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.
Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.
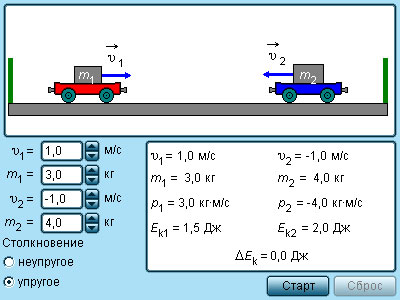 |
|
Модель. Упругие и неупругие соударения. |
Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
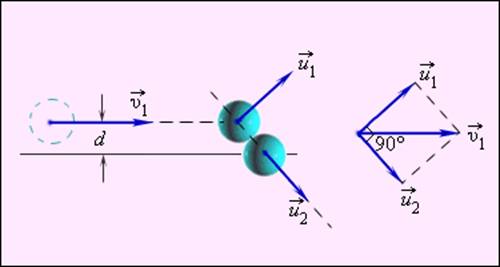
Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).
|
|
|
Рисунок 1.21.3. Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние |
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей и
после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости
налетающего шара. Если массы шаров одинаковы, то векторы скоростей
и
шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m1 = m2 = m эти законы принимают вид:
Первое из этих равенств означает, что векторы скоростей ,
и
образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами
и
равен 90°.
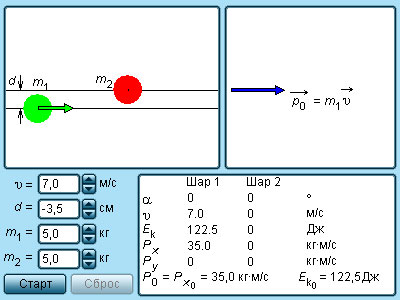 |
|
Модель. Соударения упругих шаров. |
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17980
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
Ответ: 42
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 42.9k
Unit Converter
Enter the height at which an object is being dropped into the calculator to determine the impact velocity. This calculator can also calculate the height when given the impact velocity.
- Final Velocity Calculator
- Free Fall Velocity Calculator
- Initial Velocity Calculator
- Maximum Height of a Projectile Calculator
- Angle of Impact Calculator
- Falling Force Calculator
- Impact G Force Calculator
- Average Impact Force Calculator
- Force From Height Calculator
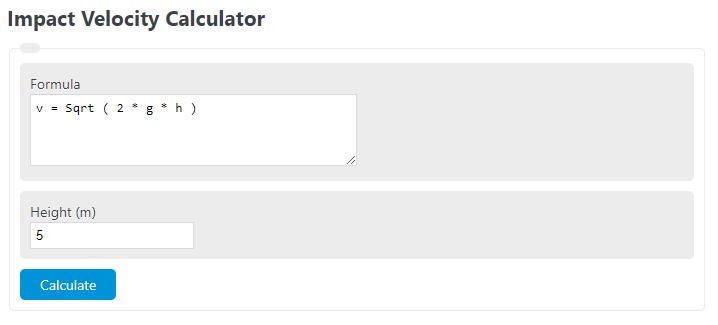
Impact Velocity Formula
The following formula is used to calculate an impact velocity.
- Where v is the impact velocity (m/s)
- g is the acceleration due to gravity (9.8 m/s^2)
- h is the height of the object (m)
To calculate impact velocity, multiply the height by 2 times the acceleration due to gravity, then take the square root of the result.
Impact Velocity Definition
An impact velocity is the total speed of an object when it makes an impact with the ground or another object after falling from a certain distance.
Impact Velocity Example
How to calculate impact velocity?
The following example goes over the necessary steps to calculate the impact velocity of a falling object given the height of the object and assuming that there is no air resistance and no other forces acting on the object.
The first step is to determine or measure the height that the object is going to be dropped from.
For this example, the height of the object is 10 meters (m).
The next and last step is to use the formula above to calculate the impact velocity:
v = Sqrt ( 2 * g * h )
v = Sqrt ( 2 * 9.81 * 10 )
v = 14.007 m/s.
FAQ
What is an impact velocity?
An impact velocity is a measure of the speed of an object when it impacts another surface. It’s most often used when analyzing objects that are dropped from a certain height.