ПЕРЕДАЧА ИНФОРМАЦИИ. РЕШЕНИЕ ЗАДАЧ
Соотношения между единицами пропускной способности канала передачи информации:
1 байт/с = 23 бит/с = 8 бит/с
1 Кбит/с = 210 бит/с = 1024 бит/с
1 Мбит/с = 210 Кбит/с = 1024 Кбит/с
1 Гбит/с = 210 Мбит/с = 1024 Мбит/с
Решение задач
I = v*t, где
I – количество передаваемой информации;
v – пропускная способность канала (скорость передачи информации);
t – время передачи информации.
-
Какое количество байтов будет передаваться за 1 секунду по каналу передачи информации с пропускной способностью 100 Мбит/с?
Дано:
v = 100 Мбит/с
t = 1 с
I – ?
I = v*t = 100*1024*1024*1/8 = 13 107 200 байт
Ответ: 12,5 Мбайт
-
Максимальная скорость передачи данных по модемному протоколу V.92 составляет 56 000 бит/c. Какое максимальное количество байт можно передать за 5 секунд по этому протоколу?
Дано:
v = 56 000 бит/с
t = 5 с
I – ?
I = v*t = 56 000*5/8 = 35 000 байт
Ответ: 35 000 байт
-
Скорость передачи данных через ADSL-соединение равна 1 024 000 бит/c. Передача файла через данное соединение заняла 5 секунд. Определите размер файла в Кбайт.
Дано:
v = 1 024 000 бит/c
t = 5 с
I – ?
I = v*t = 1 024 000*5/8 = 640 000 байт = 625 Кбайт
Ответ: 625 Кбайт
-
Скорость передачи данных составляет 56 000 бит/c. Необходимо передать файл размером 280 000 байт. Определите время передачи файла в секундах.
Дано:
v = 56 000 бит/c
I = 280 000 байт
t – ?
I = v*t; t = I/v = 280 000 * 8 / 56 000 = 40 c
Ответ: 40 секунд
Решение задач в классе
-
Скорость передачи данных составляет 56 000 бит/c. Необходимо передать файл размером 280 000 байт. Определите время передачи файла в секундах.
Дано:
v = 56 000 бит/c
I = 280 000 байт
t – ?
I = v*t; t = I/v = 280 000 * 8 / 56 000 = 40 c
Ответ: 40 секунд
-
Файл размером 64 Кбайт передаётся через некоторое соединение со скоростью 1024 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 256 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
Пояснение.
Определим время передачи:
64 Кбайт/1024 бит в секунду = (64 · 1024 · 8 бит)/(1024 бит в секунду) = 64 · 8 секунд.
Вычислим размер файла:
64 · 8 секунд · 256 бит в секунду = 64 · 256 байт = 16 Кбайт.
Ответ: 16.
-
Файл размером 160 Кбайт передаётся через некоторое соединение со скоростью 2048 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 768 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
Пояснение.
Определим время передачи:
160 Кбайт/2048 бит в секунду = (160 · 1024 · 8 бит)/(2 · 1024 бит в секунду) = 160 · 4 секунд.
Вычислим размер файла: 160 · 4 секунд · 768 бит в секунду = 60 Кбайт.
-
Файл размером 60 Кбайт передаётся через некоторое соединение со скоростью 3072 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 256 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
Пояснение.
Определим время передачи:
60 Кбайт/3072 бит в секунду = (60 · 1024 · 8 бит)/(3 · 1024 бит в секунду) = 20 · 8 секунд.
Вычислим размер файла: 20 · 8 секунд · 256 бит в секунду = 5120 · 8 бит = 5 Кбайт.
Домашнее задание 9 класс
-
Файл размером 80 Кбайт передаётся через некоторое соединение со скоростью 2048 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 768 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
-
Файл размером 120 Кбайт передаётся через некоторое соединение со скоростью 3072 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 1024 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
-
Файл размером 1000 Кбайт передаётся через некоторое соединение в течение 1 минуты. Определите размер файла (в Кбайт), который можно передать через это соединение за 36 секунд. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
Самостоятельная работа по теме «Скорость передачи данных»
-
Скорость передачи данных составляет 56 000 бит/c. Необходимо передать файл размером 280 000 байт. Определите время передачи файла в секундах.
-
Файл размером 64 Кбайт передаётся через некоторое соединение со скоростью 1024 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 256 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
-
Файл размером 160 Кбайт передаётся через некоторое соединение со скоростью 2048 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 768 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
-
Файл размером 60 Кбайт передаётся через некоторое соединение со скоростью 3072 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 256 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
-
Скорость передачи данных через ADSL-соединение равна 1 024 000 бит/c. Передача файла через данное соединение заняла 5 секунд. Определите размер файла в Кбайт.
Самостоятельная работа по теме «Скорость передачи данных»
-
Скорость передачи данных составляет 56 000 бит/c. Необходимо передать файл размером 280 000 байт. Определите время передачи файла в секундах.
-
Файл размером 64 Кбайт передаётся через некоторое соединение со скоростью 1024 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 256 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
-
Файл размером 160 Кбайт передаётся через некоторое соединение со скоростью 2048 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 768 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
-
Файл размером 60 Кбайт передаётся через некоторое соединение со скоростью 3072 бит в секунду. Определите размер файла (в Кбайт), который можно передать за то же время через другое соединение со скоростью 256 бит в секунду. В ответе укажите одно число — размер файла в Кбайт. Единицы измерения писать не нужно.
-
Скорость передачи данных через ADSL-соединение равна 1 024 000 бит/c. Передача файла через данное соединение заняла 5 секунд. Определите размер файла в Кбайт.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:
-
Скорость передачи данных через ADSL-соединение равна 256 000 бит/c. Передача файла через данное соединение заняла 16 секунд. Определите размер файла в Кбайт.
-
Скорость передачи данных составляет 56 000 бит/c. Необходимо передать файл размером 210 000 байт. Определите время передачи файла в секундах.
-
Скорость передачи данных через ADSL-соединение равна 2 621 440бит/с. Через данное соединение передают файл размером 10 Мбайт. Определите время передачи файла в секундах.
-
Скорость передачи данных через ADSL-соединение равна 256 000 бит/с. Определите наибольший размер файла в килобайтах, который может быть передан через данное соединение за 10 минут.
-
Сколько секунд потребуется модему, передающему информацию со скоростью 102 400 бит/с, чтобы передать цветное растровое изображение размером 1024×800 пикселей, при условии, что в палитре 65 536 цветов (216). Результат представьте целым числом.
-
Скорость передачи данных через ADSL-соединение равна 5 242 880 бит/с. Через данное соединение передают файл размером 1 Гбайт. Определите время передачи файла в минутах.
-
Скорость передачи данных через ADSL-соединение равна 128 000 бит/с. Определите наибольший размер файла, который может быть передан через данное соединение за 7 минут.
-
Сколько секунд потребуется модему, передающему информацию со скоростью 33 600 бит/с, чтобы передать цветное растровое изображение размером 640×480 пикселей, при условии, что в палитре 16 777 216 цветов (224). Результат представьте целым числом.
-
Скорость передачи данных через ADSL-соединение равна 256 000 бит/с. Через данное соединение передают файл размером 3,5 Мбайт. Определите время передачи файла в секундах.
-
Скорость передачи данных через ADSL-соединение равна 512 000 бит/с. Определите наибольший размер файла, который может быть передан через данное соединение за 3 минуты.
-
Сколько секунд потребуется модему, передающему информацию со скоростью 9 600 бит/с, чтобы передать цветное растровое изображение размером 1024×800 пикселей, при условии, что в палитре 16 777 216 цветов (224). Результат представьте целым числом.
-
Скорость передачи данных через ADSL-соединение равна 1 000 000 бит/с. Через данное соединение передают файл размером 100 Мбайт. Определите время передачи файла в минутах.
-
Скорость передачи данных через ADSL-соединение равна 1 000 000 бит/с. Определите наибольший размер файла, который может быть передан через данное соединение за 11 секунд.
-
Сколько секунд потребуется модему, передающему информацию со скоростью 24 000 бит/с, чтобы передать цветное растровое изображение размером 1440×800 пикселей, при условии, что в палитре 65 536 цветов (216). Результат представьте целым числом.
-
Скорость передачи данных через ADSL-соединение равна 128 000 бит/с. Через данное соединение передают файл размером 8 Мбайт. Определите время передачи файла в секундах.
-
Скорость передачи данных через ADSL-соединение равна 3 000 000 бит/с. Определите наибольший размер файла, который может быть передан через данное соединение за 9 секунд.
-
Сколько секунд потребуется модему, передающему информацию со скоростью 14 400 бит/с, чтобы передать цветное растровое изображение размером 800×600 пикселей, при условии, что в палитре 256 цветов. Результат представьте целым числом.
-
Скорость передачи данных через ADSL-соединение равна 256 000 бит/с. Через данное соединение передают файл размером 3,5 Мбайт. Определите время передачи файла в секундах.
-
Скорость передачи данных через ADSL-соединение равна 128 000 бит/с. Определите наибольший размер файла, который может быть передан через данное соединение за 7 минут.
-
Сколько секунд потребуется модему, передающему информацию со скоростью 24 000 бит/с, чтобы передать цветное растровое изображение размером 1440×800 пикселей, при условии, что в палитре 65 536 цветов (216). Результат представьте целым числом.
Скорость передачи данных
- Главная
- /
- Информатика
- /
- Скорость передачи данных
Скорость передачи данных — объём данных (информации), переданный за единицу времени (как правило 1 секунду). Базовой единицей измерения скорости передачи данных является бит в секунду. Также к базовым единицам можно отнести байт в секунду, который равен 8 битам в секунду. Все остальные единицы измерения скорости передачи данных являются производными от этих двух.
Они образуются при помощи приставок:
- используемых для обозначения десятичных кратных единиц: кило- (103), мега- (106), гига- (109) и т.д.
- используемых для обозначения 2-x кратных единиц — двоичные (бинарные) приставки: киби- (210) , меби- (220), гиби- (230) и т.д.
При этом, к примеру:
1 килобит в секунду = 1×103 = 1000 бит в секунду
1 кибибит в секунду = 1×210 = 1024 бит в секунду
1 кибибит в секунду = 1.024 килобит в секунду
1 килобит в секунду = 0.9765625 кибибит в секунду
1 килобит в секунду ≠ 1024 бит в секунду
Хотя до введения двоичных приставок международной электротехнической комиссией (МЭК) в 1999 году, принято было считать, что 1 килобит равняется именно 1024 бит. Но по сути это было не верно.
К сожалению новый стандарт до сих пор используется не повсеместно и из-за этого могут возникнуть ошибки и недопонимания.
Онлайн конвертер
Чтобы перевести скорость передачи данных из одних единиц измерения в другие, введите значение и выберите единицы измерения скорости.
Онлайн калькулятор
Скорость передачи данных
Объём данных (размер файла) I =
Время передачи данных t =
Скорость передачи данных V =
0
Округление ответа:
Объём данных
Скорость передачи данных V =
Время передачи данных t =
Объём данных (размер файла) I =
0
Округление ответа:
Время передачи данных
Объём данных (размер файла) I =
Скорость передачи данных V =
Время передачи данных t =
0
Округление ответа:
Теория
Как найти скорость передачи данных
Чему равна скорость передачи данных (V), если известен объём переданных данных (I) и время (t), за которое эти данные переданы?
Формула
V = I ⁄ t
Пример
Через некое соединение был передан файл размером 5MB (мегабайт), передача заняла 16 секунд. Необходимо определить скорость передачи данного файла в мегабитах в секунду.
Для начала переведём 5 мегабайт в биты (cм. таблицу ниже):
5MB = 5 ⋅ 8000000 = 40 000 000 бит
Далее считаем по формуле:
V = 40000000/16 = 2 500 000 бит/с
Переводим полученный результат в мегабиты в секунду:
V = 2500000/1000000 = 2.5 Мбит/с
Как найти объём данных
Чему равен объём данных (I), если известны скорость передачи данных (V) и время (t), за которое эти данные переданы?
Формула
I = V ⋅ t
Пример
Скорость передачи данных через ADSL-соединение равна 512000 бит/с. Передача файла заняла 16 секунд. Определим объем файла в килобайтах.
Для начала определим размер переданного файла в битах:
I = 512000 ⋅ 16 = 8192000 бит
Переведём полученный результат в килобайты:
I = 8192000/8000 = 1024 Кбайт
Этот результат верен если 1 Кбайт = 1000 бит. Если же вы производите расчет с устаревшими единицами (1 Кбайт = 1024 бит), то:
I = 8192000/8192 = 1000 Кбайт
А если результат записать в кибибайтах:
I = 8192000/8192 = 1000 КиБ
Как найти время передачи данных
Чему равно время передачи данных (t), если известны объём переданных данных (I) и скорость передачи данных (V):
Формула
t = I ⁄ V
Пример
За сколько секунд скачается файл размером в 1GB (гигабайт), если скорость соединения 2 Мбит/с?
1GB = 8 000 000 000 бит = 8 000 Мбит
t = 8000/2 = 4000 сек
Таблица преобразования единиц скорости передачи данных
| Обозначение RU |
Обозначение EN |
бит в секунду | байт в секунду | перевод в бит/с формула |
перевод в Б/с формула |
|
| бит в секунду | бит/с | bit/s | 1 | 0.125 | 1 | 1⁄8 |
| байт в секунду | Б/с | B/s | 8 | 1 | 8 | 1 |
| килобит в секунду | Kбит/с | kbit/s | 1,000 | 125 | 103 | 1⁄8 × 103 |
| кибибит в секунду | Кибит/с | Kibit/s | 1,024 | 128 | 210 | 27 |
| килобайт в секунду | Кбайт/с | kB/s | 8,000 | 1,000 | 8 × 103 | 103 |
| кибибайт в секунду | КиБ/с | KiB/s | 8,192 | 1,024 | 213 | 210 |
| мегабит в секунду | Мбит/с | Mbit/s | 1,000,000 | 125,000 | 106 | 1⁄8 × 106 |
| мебибит в секунду | Мибит/с | Mibit/s | 1,048,576 | 131,072 | 220 | 217 |
| мегабайт в секунду | Мбайт/с | MB/s | 8,000,000 | 1,000,000 | 8 × 106 | 106 |
| мебибайт в секунду | МиБ/с | MiB/s | 8,388,608 | 1,048,576 | 223 | 220 |
| гигабит в секунду | Гбит/с | Gbit/s | 1,000,000,000 | 125,000,000 | 109 | 1⁄8 × 109 |
| гибибит в секунду | Гибит/с | Gibit/s | 1,073,741,824 | 134,217,728 | 230 | 227 |
| гигабайт в секунду | Гбайт/с | GB/s | 8,000,000,000 | 1,000,000,000 | 8 × 109 | 109 |
| гибибайт в секунду | ГиБ/с | GiB/s | 8,589,934,592 | 1,073,741,824 | 233 | 230 |
| терабит в секунду | Тбит/с | Tbit/s | 1,000,000,000,000 | 125,000,000,000 | 1012 | 1⁄8 × 1012 |
| тебибит в секунду | Тибит/с | Tibit/s | 1,099,511,627,776 | 137,438,953,472 | 240 | 237 |
| терабайт в секунду | Тбайт/с | TB/s | 8,000,000,000,000 | 1,000,000,000,000 | 8 × 1012 | 1012 |
| тебибайт в секунду | ТиБ/с | TiB/s | 8,796,093,022,208 | 1,099,511,627,776 | 243 | 240 |
Ссылки
способности
каналов связи
В
условиях отсутствия помех скорость
передачи информации
определяется
количеством информации, переносимым
символом
сообщения
в единицу времени, и соответственно
равна:
C
= n
(9)
Где
n
—
количество символов, вырабатываемых
источником
сообщений
за единицу времени; H
—
энтропия (неопределённость),
снимаемая
при получении одного символа сообщений,
вырабатываемых
данным
источником.
Скорость
передачи информации также может быть
представлена
следующим
образом:
C
=

(10)
Где
τ
— время передачи одного двоичного
символа.
Скорость
передачи информации всегда определяется
относительно
первичного
алфавита и зависит от его энтропии, а
скорость передачи
сигналов
вычисляется относительно вторичного
алфавита (если аппаратура
обеспечивает
передачу всех качественных признаков
вторичного алфавита). Таким образом,
скорость передачи информации зависит
от информационных характеристик
источника сообщений, а скорость передачи
сигналов — от быстродействия аппаратуры.
Величины эти не следует путать, так как
они вычисляются по разным формулам и
имеют разные единицы измерения. Так, в
отличие от формулы (10), скорость передачи
сигналов может быть вычислена по формуле:
V=
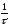
Где
τ
— время передачи одного символа
вторичного алфавита.
Для
сообщений, составленных из равновероятностных
взаимонезависимых
символов равной длительности, скорость
передачи
информации
может быть определена следующим образом:
С
=

бит/с (11)
В
случае неравновероятностных символов
равной длительности,
скорость
передачи информации определяется
согласно формуле:
C=
(12)
В
случае неравновероятностных и
взаимонезависимых символов
разной
длительности, скорость передачи
информации может быть
вычислена
следующим образом:
С
=
бит/с (13)
Где
ai—
передаваемый сигнал; bj—
сигнал, соответствующий
переданному
ai
сигналу. События A
и B
статистически жёстко связаны. При
отсутствии помех, условная вероятность
максимальна p(bj
/ ai)
= 1, а условная энтропия:
H(A/B)
=

p(bj
/ ai)
=
0,
таккакlog2p(bj
/ ai)
= log21
= 0.
При
высоком уровне помех любой из принятых
сигналов bjможетсоответствовать
любому переданному сигналу ai
— статистическая связь между переданными
и принятыми сигналами отсутствует. В
этом случае вероятности p(ai)
и p(bj)
есть вероятности независимых событий
и p(bj
/ ai)
= p(bj);
p(ai
/ bj)
= p
(ai).
Информационные
характеристики реальных каналов лежат
между этимидвумя предельными случаями.
Пропускная
способность (или ёмкость канала связи)
— есть
максимальная
скорость передачи информации по данному
каналу связи. Под каналом связи
подразумевается совокупность средств,
предназначенных для передачи информации
от данного источника сообщений к
адресату. Выражение для пропускной
способности отличается от выражения
(9) тем, что пропускную способность
характеризует максимальная
энтропия:
Сmax=

(14)
В
случае для двоичного кода, выражение
для расчёта пропускной
способности
примет вид:
Cmax
=

При
наличии помех, пропускная способность
канала связи вычисляетсякак произведение
количества принятых в секунду знаков
n на разность энтропии источника сообщений
и условной энтропии источника сообщений
относительно исходного сигнала:
Cn
=n
(15)
или
следующим образом:
Cn
=

В
общем случае:
Cn=
n
=n
(16)
Если
символы источника сообщений неравновероятны
и
взаимозависимы,
то энтропия источника вычисляется по
формуле общей
условной
энтропии.
Для
симметричных бинарных каналов, в которых
сигналы передаются при помощи двух
качественных признаков и вероятность
ложного приёмаpл
= p(1/0) = p(0/1),
а вероятность правильного приёма pп
= 1 – pл,
потери учитываются при помощи условной
энтропии вида:
H(B/A)=
бит/c
(17)
Пропускная
способность для таких каналов может
быть определена
следующим
образом:
Cn
= n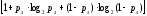
(18)
Таким
образом, формула пропускной расчёта
способности для
симметричного
бинарного канала будет иметь следующий
вид:
Cn
=

(19)
Для
симметричных дискретных каналов связи
с числом качественных
признаков
m>
2, формула расчёта пропускной способности
может быть
представлена
в следующем виде:
Cn=
бит/c
(20)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
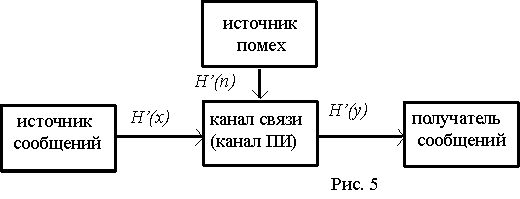
В дискретной системе связи при отсутствии помех информация на выходе канала связи (канала ПИ) полностью совпадает с информацией на его входе, поэтому скорость передачи информации численно равна производительности источника сообщений:
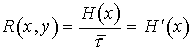
При наличии помех часть информации источника теряется и скорость передачи информации оказывается меньшей, чем производительность источника. Одновременно в сообщение на выходе канала добавляется информация о помехах (рис.5).
Поэтому при наличии помех необходимо учитывать на выходе канала не всю информацию, даваемую источником, а только взаимную информацию:
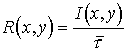
На основании формулы (20) имеем
или
, (23)
где H¢(x) – производительность источника;
H¢(x/y) – “ненадёжность” канала(потери) в единицу времени;
H¢(y) – энтропия выходного сообщения в единицу времени;
H¢(y/x)=H’(n) –энтропия помех ( шума) в единицу времени.
Пропускной способностью канала связи (канала передачи информации) C называется максимально возможная скорость передачи информации по каналу
. (24)
Для достижения максимума учитываются все возможные источники на выходе и все возможные способы кодирования.
Таким образом, пропускная способность канала связи равна максимальной производительности источника на входе канала, полностью согласованного с характеристиками этого канала, за вычетом потерь информации в канале из-за помех.
В канале без помех C=max H¢(x), так как H¢(x/y)=0. При использовании равномерного кода с основанием k, состоящего из n элементов длительностью tэ, в канале без помех
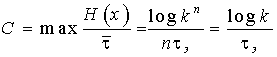
при k=2 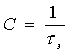
Для эффективного использования пропускной способности канала необходимо его согласование с источником информации на входе. Такое согласование возможно как для каналов связи без помех, так и для каналов с помехами на основании двух теорем, доказанных К.Шенноном.
1-ая теорема (для канала связи без помех):
Если источник сообщений имеет энтропию H (бит на символ), а канал связи – пропускную способность C (бит в секунду), то можно закодировать сообщения таким образом, чтобы передавать информацию по каналу со средней скоростью, сколь угодно близкой к величине C, но не превзойти её.
К.Шеннон предложил и метод такого кодирования, который получил название статистического или оптимального кодирования. В дальнейшем идея такого кодирования была развита в работах Фано и Хаффмена и в настоящее время широко используется на практике для “cжатия сообщений”.
2-ая теорема (для каналов связи с помехами):
Если пропускная способность канала равна C, а производительность источника H’(x)<C, то путём соответствующего кодирования можно передавать информацию по каналу связи со скоростью, сколь угодно к C и с вероятностью ошибки, сколь угодно близкой к нулю. Если же H’(x)>C, то можно закодировать источник таким образом, что ненадёжность будет меньше, чем H’(x)-C+e, где e. – сколь угодно малая величина.
Не существует способа кодирования, обеспечивающего ненадёжность, меньшую, чем H'(x)-C.
К сожалению, теорема К.Шеннона для каналов с шумами(помехами) указывает только на возможность такого кодирования, но не указывает способа построения соответствующего кода. Однако известно, что при приближении к пределу, устанавливаемому теоремой Шеннона, резко возрастает время запаздывания сигнала в устройствах кодирования и декодирования из-за увеличения длины кодового слова n. При этом вероятность ошибки на выходе канала стремится к величине
. (26)
Cледовательно, имеет место “обмен” верности передачи на скорость и задержку передачи.
Вопросы
- Что такое пропускная способность канала связи, как она определяется?
- Чему равна пропускная способность канала связи без помех?
- Как влияют помехи на величину пропускной способности?
- Что утверждает теорема Шеннона для канала связи без помех?
- Что утверждает теорема Шеннона для канала связи с помехами?
7. Передача данных. Размеры файлов.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Передача данных. Простейшие задачи на скорость, время и размер файла.
Игорь отправил файл весом (128) Кбайт своему другу. Файл пришёл другу Игоря через (64) секунды.
Укажите максимальный размер файла в Мбайтах, который сможет передать Игорь по этому же каналу связи за (512) секунд.
В ответе укажите только целое число, единицу измерение писать не нужно.
Найдём скорость данного канала связи: (cfrac{128}{64} = 2) Кбайт/с.
Найдём максимальный размер файла в Мбайтах, который можно передать за (512) секунд по этому же каналу связи: (512 cdot 2 = 1) Мбайт
Ответ: 1
Григорий сравнивает скорости двух модемов. Первый передаёт файл размером (3200) Мбайта за (256) секунд, а второй файл размером (400) Мбайт за (64) секунд.
Какой модем работает быстрее? Укажите в ответе модуль разности скоростей этих модемов в Мбит/с.
Найдём скорость первого модема в Мбит/с: (cfrac{3200 cdot 8}{256} = 100) Мбит/с
Найдём скорость второго модема в Мбит/с: (cfrac{400 cdot 8}{64} = 50) Мбит/с
(|v_1 – v_2| = 100 – 50 = 50) Мбит/с.
Ответ: 50
Анатолий сравнивает скорости двух модемов. Первый передаёт файл размером (2) Гбайта за (2048) секунд, а второй файл размером (2000) Мбайт за (4096) секунд.
Какой модем работает быстрее? Укажите в ответе модуль разности скоростей этих модемов в Кбит/с.
Найдём скорость первого модема в Кбит/с: (cfrac{2 cdot 2^{23}}{2^{11}} = 2^{13} = 8192) Кбит/с
Найдём скорость второго модема в Кбит/с: (cfrac{2000 cdot 2^{13}}{2^{12}} = 2000 cdot 2 = 4000) Кбит/с
(|v_1 – v_2| = 8192 – 4000 = 4192) Кбит/с.
Ответ: 4192
Яна отправила свой доклад, в котором (6000) символов(каждый символ кодируется (8) битами), своей подруге через канал связи со скоростью (15) Кбит/с.
Через сколько секунд доклад придёт подруге Яны? В ответе укажите только значение, единицу измерение писать не нужно.
Вес сообщения составил (6000 cdot 8 = 46,875) Кбит. Откуда время (= cfrac{46,875}{15} = 3,125) секунды.
Ответ: 3, 125
По защищённому каналу связи Школково((125) Мбит/с()) передаётся (3) файла: изображение, аудиофайл и видеофайл.
Файлы имеют следующие характеристики:
1) Изображение (-) (FullHD(1920 times 1080) пикселей().)
2) Аудиофайл (-) (64) Мбайт.
3) Видеофайл (-) (60) Мбайт.
Какое максимальное количество цветов могло быть использовать в палитре этого изображения, если передача файлов шла (8,189125) секунды?
Так как передача файлов шла (8,189125) секунды, было передано: (8,189125 cdot 125 cdot 2^{20} = 65513 cdot 2^{14}) бит.
Из них: (64) Мбайт (-) аудиофайл, (60) Мбайт (-) видеофайл.
Откуда, изображение могло занимать (65513 cdot 2^{14} – 124 cdot 2^{23} = 2025 cdot 2^{14}) бит.
Для хранения растрового изображения нужно выделить в памяти (I=N cdot i) бит, где (N) (-) количество пикселей и (i) (-) количество бит, отводимое на (1) пиксель.
Подставим известные значения в формулу: (I=N cdot i) и найдем глубину кодирования (-) (i:)
(2025 cdot 2^{14} = 1920 cdot 1080 cdot i Rightarrow 16)
Глубина кодирования (-) это количество бит, которые выделяются на хранение цвета одного пикселя. При глубине кодирования (i) бит на пиксель, код каждого пикселя выбирается из (2^i) возможных вариантов, поэтому можно использовать не более (2^i) различных цветов. Следовательно, изображение использует: (2^{16}=65536) цветов.
Ответ: 65536
По защищённому каналу связи Школково((50) Мбит/с()) передаётся (3) файла: изображение, аудиофайл и видеофайл.
Файлы имеют следующие характеристики:
1) Изображение (-) (2240) Кбайт.
2) Аудиофайл (-) (128) c; (32) кГц, глубина кодирования – (8) бит.
3) Видеофайл (-) (30) Мбайт.
Найдите количество каналов аудиозаписи, если передача файлов шла (6,4) секунды? В ответе укажите только целое число.
Так как передача файлов шла (6,4) секунды, было передано: (6,4 cdot 50 cdot 2^{20} = 320 cdot 2^{20} = 40) Мбайт.
Из них: (2,1875) Мбайт (-) изображение, (30) Мбайт (-) видеофайл.
Откуда, аудиофайл мог занимать (40 – 30 – 2,1875 = 125 cdot 2^{19}) бит.
Для хранения информации о звуке длительностью (t) секунд, закодированном с частотой дискретизации (f) Гц и глубиной кодирования (B) бит с (k) каналами записи требуется (t cdot f cdot B cdot k) бит памяти.
(f)(Гц) – частота дискретизации определяет количество отсчетов, запоминаемых за (1) секунду.
(B)(бит) – глубина кодирования – это количество бит, которые выделяются на один отсчет.
(I=tcdot f cdot Bcdot k)
(125 cdot 2^{19} = 128 cdot 32000 cdot k cdot 8 Rightarrow k = 2)
Ответ: 2
Яна сравнивает скорости двух модемов. Первый передаёт файл размером (2220000) Кбайт за (2) минуты, а второй файл размером (2250000) Кбайт за 3 минуты.
Какой модем работает быстрее? Укажите в ответе модуль разности скоростей этих модемов в Кбит/с.
Найдём скорость первого модема в Кбит/с: (cfrac{2220000 cdot 8}{2 cdot 60} = 148000) Кбит/с
Найдём скорость второго модема в Кбит/с: (cfrac{2250000 cdot 8}{3 cdot 60} = 100000) Кбит/с
(|v_1 – v_2| = 148000 – 100000 = 48000) Кбит/с.
Ответ: 48000

УСТАЛ? Просто отдохни