Вы, наверное, сразу же скажете, что скорость электрического тока равна скорости света и будете неправы. В этом материале я на простом примере объясню, каким образом и с какой скоростью перемещается электрический ток по проводам.
Давайте для примера смоделируем следующую ситуацию:
Пусть у нас будет лампочка соединенная с постоянным источником питания двужильным экранированным кабелем, причем длина этого кабеля будет 10 километров.
Теперь если мы включим выключатель в этой цепи, то лампочка загорится через 10 км/300 000 км/с, где 10 км – это длина нашего проводника, а 300 000 км/с – это скорость распространения электромагнитной волны (света) в вакууме.
То есть, произведя расчет, получается, лампочка загорится через 0,00003333 сек или 33,333 мксек (в расчет не принята емкость проводника). Из этого следует вывод, что «движение электронов» распространится по проводнику со скоростью света.
Но то обстоятельство, что электроны начинают перемещаться друг за другом со скоростью света совсем не говорит о том, что они перемещаются в проводнике с этой же скоростью.
Здесь скорость света эта та скорость, с которой заряженные частицы начинают двигаться друг за другом, а перемещаться по проводнику они могут со скоростью всего лишь несколько миллиметров в единицу времени.
Непонятно? Сейчас объясню почему так.
Итак, мы замкнули цепь, нажав выключатель. В этот момент электроны начинают покидать минусовую клемму нашего с вами конденсатора, при этом происходит уменьшение электрического поля в диэлектрике конденсатора и электроны (с подключенного проводника) начинают заходить на плюсовую клемму конденсатора.
Таким образом, разность потенциалов между обкладками конденсатора уменьшается. А по причине того, что электроны в присоединённом участке проводника пришли в движение, то их пустующее место занимают электроны из соседнего участка провода (под действием электромагнитного поля замкнутой цепи).
Этот процесс перемещения распространяется все дальше по проводнику и по истечению определенного времени достигает нашей с вами лампочки и протекающий ток заставляет ее светиться.
Получается, что изменение электрического поля по проводнику распространяется мгновенно, а вот сами заряженные частицы имеют гораздо более низкую скорость.
Аналогия с водопроводом
Давайте для простоты понимания проведем аналогию с водопроводом.
Представьте такую картину: вы запустили водяной насос, также находящийся далеко за городом и буквально через доли секунды (изменение давления распространяется со средней скоростью 1400 км/с) у вас из трубы начала поступать вода. Но эта не та же самая вода, которая только что прошла через насос, «толкотня» молекул воды распространилась с огромной скоростью, а сами молекулы движутся с гораздо меньшей скоростью.
Так и с движением электрического тока.
А как у переменного тока
Ну вроде бы с постоянным током все более-менее стало ясно и может так же возникнуть второй логичный вопрос: А как дела обстоят с переменным током?
На самом деле разница здесь заключена лишь в том, что переменный ток меняет направление своего движения с частотой 50 Герц в единицу времени. Но при этом его скорость зависит все от тех же факторов, что и в случае с постоянным током.
Заключение и выводы
Так, давайте вновь вернемся к току. Получается, если на проводник не воздействует электромагнитное поле, то движение электронов внутри провода происходит абсолютно в хаотичном порядке.
Как только к проводнику оказывается воздействие электрического поля, то в зависимости от таких факторов как температура проводника, материала, разности потенциалов, скорость электрического тока может варьироваться от 0,6 до 6 миллиметров в одну единицу времени. Как видите, эта величина очень далека от скорости света. И вычисляется она по следующей формуле:
Где n – концентрация свободных носителей, S – площадь сечения проводника, e – заряд частицы, I – сила тока.
Это все, что я хотел вам рассказать о скорости перемещения электрического тока по проводам. Если статья оказалась вам полезна, то оцените ее лайком. Спасибо за ваше внимание!
1. Вступление
Для того чтобы установить природу силы в проводнике, который движется в магнитном поле, проведём эксперимент. Предположим, что в вертикальном однородном магнитном поле с индукцией (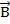 ) расположен горизонтальный проводник длиной (l), который движется с постоянной скоростью (
) расположен горизонтальный проводник длиной (l), который движется с постоянной скоростью (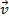 ) перпендикулярно вектору магнитной индукции магнитного поля. Если подсоединить к концам этого проводника чувствительный вольтметр, то увидим, что он покажет наличие разности потенциалов на концах этого проводника. Выясним, откуда берётся это напряжение. В данном случае нет контура и нет изменяющегося магнитного поля, поэтому мы не может сказать, что движение электронов в проводнике возникло в результате появления вихревого электрического поля. Когда проводник движется, как единое целое (рис. 1), у зарядов проводника и у положительных ионов, которые находятся в узлах кристаллической решётки, и у свободных электронов возникает скорость направленного движения.
) перпендикулярно вектору магнитной индукции магнитного поля. Если подсоединить к концам этого проводника чувствительный вольтметр, то увидим, что он покажет наличие разности потенциалов на концах этого проводника. Выясним, откуда берётся это напряжение. В данном случае нет контура и нет изменяющегося магнитного поля, поэтому мы не может сказать, что движение электронов в проводнике возникло в результате появления вихревого электрического поля. Когда проводник движется, как единое целое (рис. 1), у зарядов проводника и у положительных ионов, которые находятся в узлах кристаллической решётки, и у свободных электронов возникает скорость направленного движения.
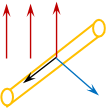
Рис. 1
На эти заряды будет действовать сила Лоренца со стороны магнитного поля. Согласно правилу «левой руки»: четыре пальца, расположенные по направлению движения, ладонь разворачиваем так, чтобы вектор магнитной индукции входил в тыльную сторону, тогда большой палец укажет действие силы Лоренца на положительные заряды.
Сила Лоренца, действующая на заряды, равна произведению модуля заряда, который она переносит, умноженной на модуль магнитной индукции, на скорость и синус угла между вектором магнитной индукции и вектором скорости.
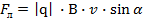 (1)
(1)
Эта сила будет совершать работу по переносу электронов на малые расстояния вдоль проводника.
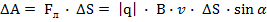 (2)
(2)
Тогда полная работа силы Лоренца вдоль проводника будет определяться силой Лоренца, умноженной на длину проводника.
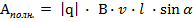 (3)
(3)
2. Природа ЭДС, возникающая при движении проводника в магнитном поле
Отношение работы сторонней силы по перемещению заряда к величине перенесённого заряда по определению ЭДС.
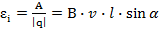 (4)
(4)
Итак, природа возникновения ЭДС индукции – это работа силы Лоренца. Однако, формулу 10.4. можно получить формально, исходя из определения ЭДС электромагнитной индукции, когда проводник перемещается в магнитном поле, пересекая линии магнитной индукции, перекрывая некоторую площадку, которую можно определить как произведение длины проводника на перемещение, которое можно выразить через скорость и время движения. ЭДС индукции по модулю равно отношению изменения магнитного потока ко времени.
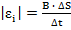 (5)
(5)
Модуль магнитной индукции постоянный, но изменяется площадь, которая покрывает проводник.
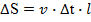 (6)
(6)
После подстановки, выражения в формулу 10.5. и сокращения получим:
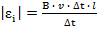 (7)
(7)
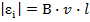 (10.8.)
(10.8.)
3. Сила Лоренца
Сила Лоренца, действующая вдоль проводника, за счёт чего происходит перераспределение зарядов – это лишь одна составляющая сил. Также имеется вторая составляющая, которая возникает именно в результате движения зарядов. Если электроны начинают перемещаться по проводнику, а проводник находится в магнитном поле, то тогда начинает действовать сила Лоренца, и направлена она будет против движения скорости проводника. Таким образом, суммирующая сила Лоренца будет равна нулю.
4. Электродвижущая сила индукции
Полученное выражение для ЭДС индукции, возникающей при движении проводника в магнитном поле, можно получить и формально, исходя из определения. ЭДС индукции равно скорости изменения магнитного потока за единицу времени, взятого со знаком минус.
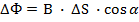
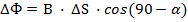
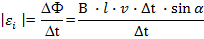
Когда неподвижный проводник находится в изменяющемся магнитном поле и когда сам проводник движется в постоянном магнитном поле, возникает явление электромагнитной индукции. И в том, и в другом случае возникает ЭДС индукции. Однако природа этой силы различна.
Электрический ток. Сила тока
- Подробности
- Обновлено 13.08.2018 19:44
- Просмотров: 878
«Физика – 10 класс»
Электрический ток — направленное движение заряженных частиц. Благодаря электрическому току освещаются квартиры, приводятся в движение станки, нагреваются конфорки на электроплитах, работает радиоприемник и т. д.
Рассмотрим наиболее простой случай направленного движения заряженных частиц — постоянный ток.
Какой электрический заряд называется элементарным?
Чему равен элементарный электрический заряд?
Чем различаются заряды в проводнике и диэлектрике?

При движении заряженных частиц в проводнике происходит перенос электрического заряда из одной точки в другую. Однако если заряженные частицы совершают беспорядочное тепловое движение, как, например, свободные электроны в металле, то переноса заряда не происходит (рис. 15.1, а). Поперечное сечение проводника в среднем пересекает одинаковое число электронов в двух противоположных направлениях. Электрический заряд переносится через поперечное сечение проводника лишь в том случае, если наряду с беспорядочным движением электроны участвуют в направленном движении (рис. 15.1, б). В этом случае говорят, что по проводнику идёт электрический ток.
Электрическим током называют упорядоченное (направленное) движение заряженных частиц.
Электрический ток имеет определённое направление.
За направление тока принимают направление движения положительно заряженных частиц.
Если перемещать нейтральное в целом тело, то, несмотря на упорядоченное движение огромного числа электронов и атомных ядер, электрический ток не возникнет. Полный заряд, переносимый через любое сечение, будет при этом равным нулю, так как заряды разных знаков перемещаются с одинаковой средней скоростью.
Направление тока совпадает с направлением вектора напряжённости электрического поля. Если ток образован движением отрицательно заряженных частиц, то направление тока считают противоположным направлению движения частиц.
Выбор направления тока не очень удачен, так как в большинстве случаев ток представляет собой упорядоченное движение электронов — отрицательно заряженных частиц. Выбор направления тока был сделан в то время, когда о свободных электронах в металлах ещё ничего не знали.
Действие тока.
Движение частиц в проводнике мы непосредственно не видим. О наличии электрического тока приходится судить по тем действиям или явлениям, которые его сопровождают.
Во-первых, проводник, по которому идёт ток, нагревается.
Во-вторых, электрический ток может изменять химический состав проводника: например, выделять его химические составные части (медь из раствора медного купороса и т. д.).
В-третьих, ток оказывает силовое воздействие на соседние токи и намагниченные тела. Это действие тока называется магнитным.
Так, магнитная стрелка вблизи проводника с током поворачивается. Магнитное действие тока в отличие от химического и теплового является основным, так как проявляется у всех без исключения проводников. Химическое действие тока наблюдается лишь у растворов и расплавов электролитов, а нагревание отсутствует у сверхпроводников.
В лампочке накаливания вследствие прохождения электрического тока излучается видимый свет, а электродвигатель совершает механическую работу.
Сила тока.
Если в цепи идёт электрический ток, то это означает, что через поперечное сечение проводника всё время переносится электрический заряд.
Заряд, перенесённый в единицу времени, служит основной количественной характеристикой тока, называемой силой тока.
Если через поперечное сечение проводника за время Δt переносится заряд Δq, то среднее значение силы тока равно:

Средняя сила тока равна отношению заряда Δq, прошедшего через поперечное сечение проводника за промежуток времени Δt, к этому промежутку времени.
Если сила тока со временем не меняется, то ток называют постоянным.
Сила переменного тока в данный момент времени определяется также по формуле (15.1), но промежуток времени Δt в таком случае должен быть очень мал.
Сила тока, подобно заряду, — величина скалярная. Она может быть как положительной, так и отрицательной. Знак силы тока зависит от того, какое из направлений обхода контура принять за положительное. Сила тока I > 0, если направление тока совпадает с условно выбранным положительным направлением вдоль проводника. В противном случае I < 0.
Термин сила тока нельзя считать удачным, так как понятие сила, применяемое к току, не имеет никакого отношения к понятию сила в механике. Но термин сила тока был введён давно и утвердился в науке.
Связь силы тока со скоростью направленного движения частиц.
Пусть цилиндрический проводник (рис. 15.2) имеет поперечное сечение площадью S.

За положительное направление тока в проводнике примем направление слева направо. Заряд каждой частицы будем считать равным q0. В объёме проводника, ограниченном поперечными сечениями 1 и 2 с расстоянием Δl между ними, содержится nSΔl частиц, где n — концентрация частиц (носителей тока). Их общий заряд в выбранном объёме q = q0nSΔl. Если частицы движутся слева направо со средней скоростью υ, то за время  все частицы, заключенные в рассматриваемом объёме, пройдут через поперечное сечение 2. Поэтому сила тока равна:
все частицы, заключенные в рассматриваемом объёме, пройдут через поперечное сечение 2. Поэтому сила тока равна:

В СИ единицей силы тока является ампер (А).
Эта единица установлена на основе магнитного взаимодействия токов.
Измеряют силу тока амперметрами. Принцип устройства этих приборов основан на магнитном действии тока.
Скорость упорядоченного движения электронов в проводнике.
Найдём скорость упорядоченного перемещения электронов в металлическом проводнике. Согласно формуле (15.2)  где е — модуль заряда электрона.
где е — модуль заряда электрона.
Пусть, например, сила тока I = 1 А, а площадь поперечного сечения проводника S = 10-6 м2. Модуль заряда электрона е = 1,6 • 10-19 Кл. Число электронов в 1 м3 меди равно числу атомов в этом объёме, так как один из валентных электронов каждого атома меди является свободным. Это число есть n ≈ 8,5 • 1028 м-3 (это число можно определить, если решить задачу 6 из § 54). Следовательно,

Как видите, скорость упорядоченного перемещения электронов очень мала. Она во много раз меньше скорости теплового движения электронов в металле.
Условия, необходимые для существования электрического тока.
Для возникновения и существования постоянного электрического тока в веществе необходимо наличие свободных заряженных частиц.
Однако этого ещё недостаточно для возникновения тока.
Для создания и поддержания упорядоченного движения заряженных частиц необходима сила, действующая на них в определённом направлении.
Если эта сила перестанет действовать, то упорядоченное движение заряженных частиц прекратится из-за столкновений с ионами кристаллической решётки металлов или нейтральными молекулами электролитов и электроны будут двигаться беспорядочно.
На заряженные частицы, как мы знаем, действует электрическое поле с силой:

Обычно именно электрическое поле внутри проводника служит причиной, вызывающей и поддерживающей упорядоченное движение заряженных частиц.
Только в статическом случае, когда заряды покоятся, электрическое поле внутри проводника равно нулю.
Если внутри проводника имеется электрическое поле, то между концами проводника в соответствии с формулой (14.21) существует разность потенциалов. Как показал эксперимент, когда разность потенциалов не меняется во времени, в проводнике устанавливается постоянный электрический ток. Вдоль проводника потенциал уменьшается от максимального значения на одном конце проводника до минимального на другом, так как положительный заряд под действием сил поля перемещается в сторону убывания потенциала.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы постоянного тока – Физика, учебник для 10 класса – Класс!ная физика
Электрический ток. Сила тока —
Закон Ома для участка цепи. Сопротивление —
Электрические цепи. Последовательное и параллельное соединения проводников —
Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» —
Работа и мощность постоянного тока —
Электродвижущая сила —
Закон Ома для полной цепи —
Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»
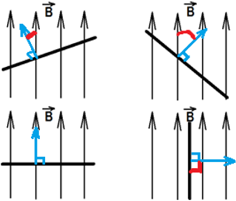
Магнитный поток, проходящий через площадь S равен:
Ф = BScosα;
где:
Ф ― величина магнитного потока [Вб],
S ― площадь контура [м2],
B ― индукция магнитного поля [Тл],
α ― угол между нормалью  к площади контура и вектором индукции магнитного поля
к площади контура и вектором индукции магнитного поля  .
.
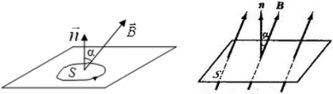
Если вектор индукции магнитного поля  перпендикулярен площади контура, то магнитный поток равен:
перпендикулярен площади контура, то магнитный поток равен:
Ф = BScos90° = BS;
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором  и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.
и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.
Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.
ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.
Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

где:
 ― ЭДС электромагнитной индукции [B],
― ЭДС электромагнитной индукции [B],
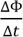 ― скорость изменения магнитного потока [Вб/с],
― скорость изменения магнитного потока [Вб/с],
∆Ф ― изменение магнитного потока [Вб],
∆t ― время, за которое происходит это изменение [c].
Кроме того, ЭДС индукции равна производной магнитного потока по времени:

где:
- ― ЭДС электромагнитной индукции [B],
- ― производная магнитного потока по времени [Вб/с].
Задача 1
Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?
Решение:
Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.
Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.
По закону электромагнитной индукции 
ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени 
И это очень важный момент, без которого мы не сможем решить такого рода задачу.
Теперь посчитаем ЭДС индукции.
Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.
ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобочках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.
Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса
 .
.
Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что 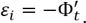
Подставив сюда значение производной, получим  = abS · sin (bt).
= abS · sin (bt).
Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.
По закону Ома  , подставив сюда значение ЭДС, получаем
, подставив сюда значение ЭДС, получаем 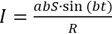 .
.
Мы получили зависимость силы тока от времени.
Из-за синуса, который стоит в этой формуле, ток постоянно меняет своё значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.
В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.
Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, 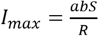 .
.
Отсюда можно легко выразить площадь контура  , подставив сюда все значения, получим
, подставив сюда все значения, получим 
Ответ: 0,002
Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:
Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:
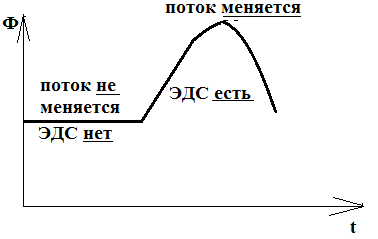
Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.
Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.
Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.
Задача 2
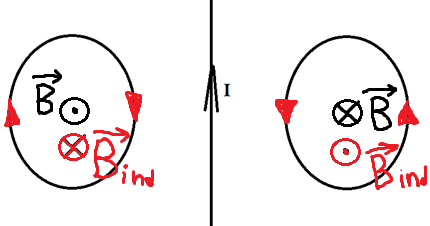
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?
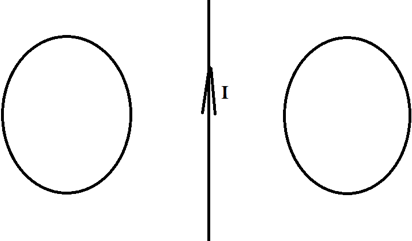
Решение:
Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?
Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.
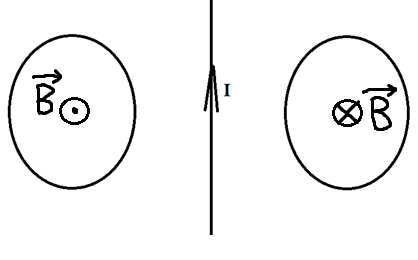
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?
Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.
Движение проводников
Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС  ;
;
где:
 ― ЭДС электромагнитной индукции [B],
― ЭДС электромагнитной индукции [B],
B ― индукция магнитного поля [Тл],
l ― длина проводника [м],
v ― скорость движения проводника [м/с],
α ― угол между направлением вектора скорости 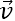 и длиной проводника
и длиной проводника  , если вектор индукции магнитного поля
, если вектор индукции магнитного поля 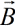 перпендикулярен проводнику и вектору скорости его движения:
перпендикулярен проводнику и вектору скорости его движения: 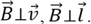
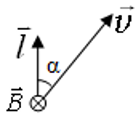
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.
В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создает ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.
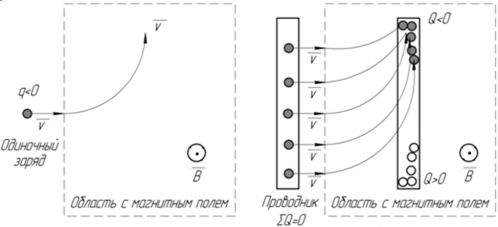
В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.
В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;
где:
U — разность потенциалов [В],
l — длина проводника [м],
v — скорость движения проводника 
B — индукция магнитного поля [Тл],
α — угол между направлением скорости и длиной проводника.
В случае, если есть какой-то замкнутый контур, то ЭДС в нём возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.
В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу 
В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу  =U= lvBsinα.
=U= lvBsinα.
Задача 3
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?
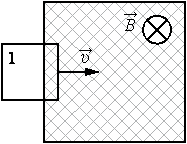
Решение:
Составим цепочку.
Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.
Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.
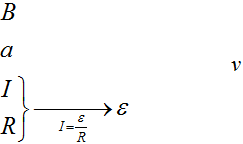
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.
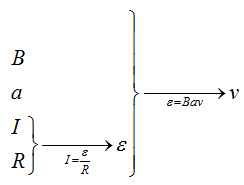
Пройдёмся вдоль этой цепочки.
Запишем закон Ома  , подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим
, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим  отсюда выразим скорость, и, подставив все величины, получим
отсюда выразим скорость, и, подставив все величины, получим 
Ответ: 1
|
|
Макеты страниц
ДВИЖУЩИЙСЯ ПРОВОДНИК в МАГНИТНОМ, ПОЛЕ
Допустим, что в магнитном поле В находится металлический проводник; на рис. III.64 показан небольшой его участок длиной  Свободные электроны, имеющиеся в этом проводнике, участвуют в тепловом движении, и в данный момент времени скорости их
Свободные электроны, имеющиеся в этом проводнике, участвуют в тепловом движении, и в данный момент времени скорости их 
различны и беспорядочно ориентированы в пространстве. Магнитное поле действует на каждый электрон с силой  направление которой перпендикулярно скорости
направление которой перпендикулярно скорости  и полю В. Так как скорости теплового движения электронов ориентированы беспорядочно, то и силы
и полю В. Так как скорости теплового движения электронов ориентированы беспорядочно, то и силы  действующие на различные электроны, а также силы, действующие на один электрон в различные моменты времени, имеют всевозможные направления. Таким образом, магнитное поле не может «навести порядок» в тепловом движении зарядов, т. е. создать их упорядоченное одностороннее перемещение. Это означает, что при рассмотрении вопроса о воздействии магнитного поля на свободные электроны можно отвлечься от их теплового движения и полагать, что все они покоятся в объеме металла.
действующие на различные электроны, а также силы, действующие на один электрон в различные моменты времени, имеют всевозможные направления. Таким образом, магнитное поле не может «навести порядок» в тепловом движении зарядов, т. е. создать их упорядоченное одностороннее перемещение. Это означает, что при рассмотрении вопроса о воздействии магнитного поля на свободные электроны можно отвлечься от их теплового движения и полагать, что все они покоятся в объеме металла.
Если проводник движется в магнитном поле с некоторой скоростью  то эта скорость накладывается на скорости беспорядочного теплового движения электронов.
то эта скорость накладывается на скорости беспорядочного теплового движения электронов.

Рис. III.64
Условившись исключить из рассуждений тепловое движение электронов, предположим, что все они вместе с проводником движутся в магнитном поле с одной и той же скоростью  Тогда на каждый электрон со стороны магйитного поля действует одна и та же сила
Тогда на каждый электрон со стороны магйитного поля действует одна и та же сила 

где  заряд электрона; а — угол между векторами
заряд электрона; а — угол между векторами 
Смещение электронов в направлении действия силы вызывает их скопление в сечении 2 и уменьшает их концентрацию в сечении  Это перераспределение зарядов в пределах объема проводника
Это перераспределение зарядов в пределах объема проводника  сопровождается появлением внутри него электрического поля, напряженность которого
сопровождается появлением внутри него электрического поля, напряженность которого  направлена от сечения 1 к сечению
направлена от сечения 1 к сечению  это поле действует на отрицательные электроны с силой
это поле действует на отрицательные электроны с силой  направленной против
направленной против  Рассмотрим два случая:
Рассмотрим два случая:
1) если в магнитном поле движется незамкнутый проводник длиной  то электрическое поле
то электрическое поле  со временем приостановит движение зарядов в направлении действия силы
со временем приостановит движение зарядов в направлении действия силы  Равновесное распределение зарядов в проводнике наступит (при постоянстве скорости движения зарядов
Равновесное распределение зарядов в проводнике наступит (при постоянстве скорости движения зарядов  и индукции магнитного поля В) при условии
и индукции магнитного поля В) при условии

Из постоянства  и В следует постоянство
и В следует постоянство  и
и  Электрическое поле внутри участка
Электрическое поле внутри участка  однородное, поэтому разность потенциалов между сечениями 1 и 2
однородное, поэтому разность потенциалов между сечениями 1 и 2

2) если проводник замыкается за пределами магнитного поля (полагаем, что поле В действует на электроны, находящиеся только в пределах участка  поле
поле  вызовет движение электронов через внешние участки цепи; по проводнику потечет электрический ток.
вызовет движение электронов через внешние участки цепи; по проводнику потечет электрический ток.
Таким образом, участки проводника, перемещающиеся в магнитном поле, можно рассматривать как «источники тока», обладающие особой электродвижущей силой, которую называют электродвижущей силой индукции. Э. д. с. индукции некоторого участка проводника  можно найти по разности потенциалов на его концах, если проводник не замкнут.
можно найти по разности потенциалов на его концах, если проводник не замкнут.

Рис. III.65
Из соотношения (3.33) и формулы (3.34) найдем напряженность электрического поля в проводнике  в зависимости от
в зависимости от  и В:
и В:

Тогда разность потенциалов на концах участка проводника

В этой формуле учтен только угол а между векторами скорости проводника  и магнитного поля В. Однако в общем случае сам проводник может быть не перпендикулярен
и магнитного поля В. Однако в общем случае сам проводник может быть не перпендикулярен  как это предполагалось выше и показано на рис. II 1.64, а ориентирован произвольным образом. Тогда следует учесть, что сила
как это предполагалось выше и показано на рис. II 1.64, а ориентирован произвольным образом. Тогда следует учесть, что сила  которая всегда перпендикулярна
которая всегда перпендикулярна  не будет уже направлена вдоль проводника, а составляет с ним некоторый угол
не будет уже направлена вдоль проводника, а составляет с ним некоторый угол  (рис. II 1.65, а). Очевидно, в этом случае движение электронов в проводнике вызывается не всей силой
(рис. II 1.65, а). Очевидно, в этом случае движение электронов в проводнике вызывается не всей силой  а только ее проекцией
а только ее проекцией  Для равновесного состояния вместо формулы (3.34) следует писать
Для равновесного состояния вместо формулы (3.34) следует писать  и тогда
и тогда

Однако для упрощения рассуждений в дальнейшем будем всегда полагать, что  что проводник перпендикулярен плоскости, в которой лежат векторы
что проводник перпендикулярен плоскости, в которой лежат векторы 
Формула (3.37) для э. д. с. индукции записывается и в другом, более общем виде. Сделаем еще одно упрощение: допустим, что векторы  и В перпендикулярны между собой, т. е.
и В перпендикулярны между собой, т. е.  Так как
Так как  площадь, описываемая проводником при его движении за время
площадь, описываемая проводником при его движении за время  (см. рис. III.64),
(см. рис. III.64),  магнитный поток, проходящий через эту площадь, то
магнитный поток, проходящий через эту площадь, то

т. е. электродвижущая сила, возникающая при движении проводника в магнитном поле, численно равна магнитному потоку через площадь, которую этот проводник описывает в единицу времени. Этот вывод можно получить и в общем случае, когда  и проводник ориентирован в магнитном поле любым образом. В частности, если прямолинейный проводник параллелен вектору В, то магнитный поток через описываемую им площадь равен нулю; в этом случае на концах проводника разности потенциалов не возникает. Заметим, что в приведенных выше формулах для
и проводник ориентирован в магнитном поле любым образом. В частности, если прямолинейный проводник параллелен вектору В, то магнитный поток через описываемую им площадь равен нулю; в этом случае на концах проводника разности потенциалов не возникает. Заметим, что в приведенных выше формулах для  знак минус вовсе не связан с тем, что рассматриваются силы, действующие на отрицательно заряженные электроны. Повторив рассуждения для свободных положительных зарядов, можно получить те же самые формулы (3.37) и (3.39).
знак минус вовсе не связан с тем, что рассматриваются силы, действующие на отрицательно заряженные электроны. Повторив рассуждения для свободных положительных зарядов, можно получить те же самые формулы (3.37) и (3.39).
Если проводник имеет сложную форму и движется в неоднородном магнитном поле, то его можно разделить на такие элементарные участки  и рассматривать такие малые перемещения
и рассматривать такие малые перемещения  Чтобы для каждого участка в пределах описываемых ими площадок
Чтобы для каждого участка в пределах описываемых ими площадок  можно было магнитное поле считать однородным. Затем можно произвести суммирование элементарных э. д. с.:
можно было магнитное поле считать однородным. Затем можно произвести суммирование элементарных э. д. с.:

В пределе, когда участки  бесконечно малые и
бесконечно малые и  мы получим точную формулу (3.39).
мы получим точную формулу (3.39).
Формулы (3.37) и (3.39) можно применять и для замкнутых контуров. Однако как только по проводнику потечет ток, т. е. начнется упорядоченное движение электронов вдоль проводника, скорость перемещения электронов относительно магнитного поля уже не будет равна скорости проводника. Обозначим скорость упорядоченного движения электронов вдоль проводника через  а скорость их перемещения вместе с проводником — через
а скорость их перемещения вместе с проводником — через  (рис. III.65,б). В этом случае сила действующая на электрон со стороны магнитного поля, будет составлять с проводником угол
(рис. III.65,б). В этом случае сила действующая на электрон со стороны магнитного поля, будет составлять с проводником угол  .
.
Разложим силу  на составляющие:
на составляющие:  ориентированную вдоль проводника по направлению движения электронов, и
ориентированную вдоль проводника по направлению движения электронов, и  направленную против движения проводника. Сила
направленную против движения проводника. Сила  совершает положительную работу, сообщая электронам энергию, которую они расходуют при
совершает положительную работу, сообщая электронам энергию, которую они расходуют при
своем движении по контуру. Сила  препятствует движению проводника и совершает отрицательную работу.
препятствует движению проводника и совершает отрицательную работу.
Сумма работ, совершаемых этими силами за какой-нибудь отрезок времени, должна быть равна работе силы  за то же время, т. е. должна равняться нулю, так как сила
за то же время, т. е. должна равняться нулю, так как сила  перпендикулярна скорости движения электронов
перпендикулярна скорости движения электронов  и поэтому работы не совершает. Таким образом, положительная работа силы по величине равна отрицательной работе силы
и поэтому работы не совершает. Таким образом, положительная работа силы по величине равна отрицательной работе силы 
Если к проводнику не прилагать внешней силы, то силы  со временем остановят его (как только будет израсходована кинетическая энергия этого проводника). Для того чтобы поддержать движение проводника
со временем остановят его (как только будет израсходована кинетическая энергия этого проводника). Для того чтобы поддержать движение проводника  скоростью
скоростью  к нему необходимо приложить внешнюю силу
к нему необходимо приложить внешнюю силу  равную сумме всех сил
равную сумме всех сил  и направленную в сторону движения. Если в единице объема проводника имеется
и направленную в сторону движения. Если в единице объема проводника имеется  электронов, участвующих в токе, то на участке длиной
электронов, участвующих в токе, то на участке длиной  и сечением
и сечением  их будет
их будет  Сила
Сила  Тогда сумма всех сил
Тогда сумма всех сил  равна
равна

(так как  сила тока в проводнике I). Заметим, что 2/2 равна амперовой силе, действующей на проводник с током со стороны магнитного поля.
сила тока в проводнике I). Заметим, что 2/2 равна амперовой силе, действующей на проводник с током со стороны магнитного поля.
Таким образом, для того чтобы вызвать в проводнике электрический ток, перемещая его в магнитном поле, необходимо преодолеть амперову силу, действующую на появившийся ток со стороны того же магнитного поля. Положительная работа приложенной внешней силы  равна положительной работе сторонних
равна положительной работе сторонних  вызывающих движение электронов в проводнике. Следовательно, источником энергии индукционных токов (т. е. токов, возбуждаемых э. д. с. индукции) является работа внешних сил, приложенных к движущемуся проводнику. Если же проводник не замкнут, то упорядоченное движение электронов в проводнике существует только в течение малого отрезка времени, пока устанавливается равновесное распределение зарядов; после наступления равновесия
вызывающих движение электронов в проводнике. Следовательно, источником энергии индукционных токов (т. е. токов, возбуждаемых э. д. с. индукции) является работа внешних сил, приложенных к движущемуся проводнику. Если же проводник не замкнут, то упорядоченное движение электронов в проводнике существует только в течение малого отрезка времени, пока устанавливается равновесное распределение зарядов; после наступления равновесия  и необходимости во внешней силе
и необходимости во внешней силе  нет.
нет.
Оглавление
- ПРЕДИСЛОВИЕ
- Часть I. МЕХАНИКА
- § 1. СИСТЕМЫ ОТСЧЕТА; ЛИНЕЙНЫЕ И УГЛОВЫЕ СКОРОСТИ И УСКОРЕНИЯ
- ДВИЖЕНИЕ ПО КРИВОЛИНЕЙНОЙ ТРАЕКТОРИИ
- § 2. ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦ
- СИЛА. ДЕФОРМАЦИЯ. МАССА
- ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ
- ИМПУЛЬС. РАБОТА. МОЩНОСТЬ
- ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- ГРАВИТАЦИОННОЕ ПОЛЕ. ВЕС ТЕЛА
- ДВИЖЕНИЕ КОСМИЧЕСКИХ ОБЪЕКТОВ
- § 4. ДВИЖЕНИЕ ТЕЛ С ПЕРЕМЕННОЙ МАССОЙ
- § 5. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ
- ПРЕОБРАЗОВАНИЯ КООРДИНАТ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Глава 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА; МОМЕНТ ИНЕРЦИИ ТЕЛ
- § 7. ЗАКОНЫ МЕХАНИКИ ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
- § 8. СВОБОДНЫЕ ОСИ. БАЛАНСИРОВКА РОТОРОВ. ГИРОСКОПЫ
- Глава 3. ЗАКОНЫ СОХРАНЕНИЯ В СИСТЕМЕ ВЗАИМОДЕЙСТВУЮЩИХ ТЕЛ
- § 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА (МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- § 12. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ НЕКОТОРЫХ СИСТЕМ
- § 13. СТОЛКНОВЕНИЕ ШАРОВ
- § 14. О ЦЕНТРЕ МАСС СИСТЕМЫ
- Глава 4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ
- § 15. ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
- § 16. СКОРОСТЬ И УСКОРЕНИЕ КОЛЕБЛЮЩЕГОСЯ ТЕЛА. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- § 17. СИЛА И ЭНЕРГИЯ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ. ПРОСТЕЙШИЕ МЕХАНИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- § 18. СОБСТВЕННЫЕ, СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ
- § 19. ПОНЯТИЕ О НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ
- § 20. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ КОЛЕБАНИЙ
- § 21. АВТОКОЛЕБАНИЯ
- Глава 5. ВОЛНОВЫЕ ПРОЦЕССЫ; ОСНОВЫ АКУСТИКИ
- § 22. ОБРАЗОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ
- § 23. ФОРМУЛА ГАРМОНИЧЕСКОЙ ВОЛНЫ
- ВОЛНА В УПРУГОЙ СРЕДЕ
- § 24. ПОТОК ЭНЕРГИИ В ВОЛНОВЫХ ПРОЦЕССАХ
- § 25. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ДИСПЕРСИЕЙ
- § 26. СТОЯЧИЕ ВОЛНЫ
- § 27. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ЭФФЕКТ ДОПЛЕРА
- ХАРАКТЕРИСТИКИ ЗВУКОВОГО ОЩУЩЕНИЯ
- § 28. УЛЬТРАЗВУКИ И ИХ ПРИМЕНЕНИЯ
- Глава 6. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ
- § 29. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
- § 30. ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИ
- СЖИМАЕМОСТЬ И ВЯЗКОСТЬ В ПОТОКЕ
- РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ЛАМИНАРНОМ ПОТОКЕ
- Часть II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
- § 1. ТЕПЛОВОЕ ДВИЖЕНИЕ
- § 2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ; ЭНЕРГИЯ СВЯЗИ МОЛЕКУЛ
- § 3. АГРЕГАТНЫЕ СОСТОЯНИЯ И ФАЗОВЫЕ ПЕРЕХОДЫ. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ И ПРОЦЕССЫ
- СВОЙСТВА ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
- ВИДЫ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ
- § 4. ВНУТРЕННЯЯ ЭНЕРГИЯ ТЕРМОДИНАМИЧЕСКОЙ СИСТЕМЫ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- § 5. ВНЕШНЯЯ РАБОТА СИСТЕМЫ И ТЕПЛООБМЕН С ОКРУЖАЮЩЕЙ СРЕДОЙ. ТЕПЛОЕМКОСТЬ ТЕЛ
- § 6. ИЗОПРОЦЕССЫ; АДИАБАТИЧЕСКИЙ ПРОЦЕСС. ЭНТРОПИЯ СИСТЕМЫ. ЗАМКНУТЫЕ (КРУГОВЫЕ) ПРОЦЕССЫ
- ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИЗОПРОЦЕССОВ
- КРУГОВЫЕ ПРОЦЕССЫ
- § 7. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИ
- ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ
- ЭНТРОПИЯ И ВЕРОЯТНОСТЬ
- Глава 2. ИДЕАЛЬНЫЙ ГАЗ
- § 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. СРЕДНИЕ СКОРОСТИ МОЛЕКУЛ
- § 9. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 10. ИЗОПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ; ТЕПЛОЕМКОСТИ ГАЗОВ
- § 11. КРУГОВЫЕ ПРОЦЕССЫ, СОВЕРШАЕМЫЕ ИДЕАЛЬНЫМ ГАЗОМ; ЦИКЛ КАРНО. ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА
- ЦИКЛ КАРНО
- ПРОЦЕССЫ, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЕ ЭНТРОПИИ
- ПАРАДОКС ГИББСА
- § 12. ДИФФУЗИЯ, ТЕПЛОПРОВОДНОСТЬ И ВНУТРЕННЕЕ ТРЕНИЕ В ГАЗАХ; ЧИСЛО СТОЛКНОВЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- Глава 3. РЕАЛЬНЫЕ ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ТЕЛА
- § 13. ОТСТУПЛЕНИЯ ОТ ЗАКОНОВ ИДЕАЛЬНЫХ ГАЗОВ. НАСЫЩЕННЫЕ ПАРЫ. КРИТИЧЕСКОЕ СОСТОЯНИЕ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГАЗОВ
- ПАР
- ПЕРЕХОДЫ в СИСТЕМЕ ЖИДКОСТЬ — ПАР — ГАЗ
- § 14. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- ПАРАМЕТРЫ КРИТИЧЕСКОГО СОСТОЯНИЯ
- ПРИМЕНЕНИЯ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- § 15. ЖИДКОСТИ; ИХ ОСНОВНЫЕ СВОЙСТВА. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ И ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
- СВОЙСТВА ЖИДКОСТЕЙ
- МОЛЕКУЛЯРНЫЕ СИЛЫ В ПОВЕРХНОСТНОМ СЛОЕ
- § 16. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- § 17. ИСПАРЕНИЕ И КИПЕНИЕ ЖИДКОСТЕЙ; КОНДЕНСАЦИЯ ПАРОВ
- ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- КИПЕНИЕ
- УДЕЛЬНАЯ ТЕПЛОТА ПАРООБРАЗОВАНИЯ
- § 18. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ
- КРИСТАЛЛИЗАЦИЯ
- ТЕМПЕРАТУРА ПЛАВЛЕНИЯ
- ТРОЙНАЯ ТОЧКА
- § 19. ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК. ТЕПЛОВЫЕ И УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- ТЕПЛОЕМКОСТЬ КРИСТАЛЛА
- ТЕПЛОВОЕ РАСШИРЕНИЕ КРИСТАЛЛОВ
- УПРУГОСТЬ И ПЛАСТИЧНОСТЬ
- ЖИДКИЕ КРИСТАЛЛЫ
- Часть III. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
- § 1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
- § 2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ; ИНДУКЦИЯ И НАПРЯЖЕННОСТЬ ПОЛЯ. ЗАКОН КУЛОНА
- § 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ СИСТЕМЫ ЗАРЯДОВ; ТЕОРЕМА ОСТРОГРАДСКОГО—ГАУССА
- ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО—ГАУССА
- ФОРМУЛЫ ДЛЯ НАПРЯЖЕННОСТИ ПОЛЯ
- § 4. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ; РАЗНОСТЬ ПОТЕНЦИАЛОВ. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЗАРЯДОВ
- § 5. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 6. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
- ЭЛЕКТРОСТРИКЦИЯ
- ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- СЕГНЕТОЭЛЕКТРИКИ
- ЭЛЕКТРЕТЫ
- § 7. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА. ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯ
- Глава 2. ЭЛЕКТРИЧЕСКИЙ ТОК
- § 8. ЭЛЕКТРИЧЕСКИЙ ТОК ПРОВОДИМОСТИ; ПЛОТНОСТЬ ТОКА
- § 9. ЭЛЕКТРОННАЯ ТЕОРИЯ ПРОВОДИМОСТИ МЕТАЛЛОВ. ЗАКОНЫ ОМА И ДЖОУЛЯ—ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ. СВЯЗЬ МЕЖДУ ЭЛЕКТРОПРОВОДНОСТЬЮ И ТЕПЛОПРОВОДНОСТЬЮ
- § 10. РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ. СВЕРХПРОВОДИМОСТЬ
- § 11. ЭЛЕКТРОДВИЖУЩАЯ СИЛА; ЗАКОН ОМА И ПРАВИЛА КИРХГОФА
- ЗАКОН ОМА ДЛЯ ЗАМКНУТОГО КОНТУРА
- ПРАВИЛА КИРХГОФА
- ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР ТОКА
- § 12. РАБОТА ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА. КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
- ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА
- КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
- ЗАКОН ВОЛЬТА. ТЕРМОЭЛЕМЕНТЫ
- ЭФФЕКТ ПЕЛЬТЬЕ
- § 13. ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ. ЭЛЕКТРОННАЯ ЛАМПА
- § 14. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ. ПОНЯТИЕ О ПЛАЗМЕ
- ДВИЖЕНИЕ ИОНОВ В ГАЗЕ
- ВИДЫ РАЗРЯДОВ В ГАЗАХ
- ПЛАЗМА
- § 15. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ. ЗАКОНЫ ФАРАДЕЯ
- § 16. ПОЛУПРОВОДНИКИ И ИХ ПРИМЕНЕНИЯ
- ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
- ЯВЛЕНИЯ НА ГРАНИЦЕ ДВУХ ПОЛУПРОВОДНИКОВ
- ПРИМЕНЕНИЯ ПОЛУПРОВОДНИКОВ
- Глава 3. ЭЛЕКТРОМАГНЕТИЗМ
- § 17. МАГНИТНОЕ ПОЛЕ
- § 18. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ ВОКРУГ ДВИЖУЩЕГОСЯ ЗАРЯДА И ПРОВОДНИКОВ С ТОКАМИ
- § 19. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ; СИЛА ЛОРЕНЦА И ЗАКОН АМПЕРА. ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ
- § 20. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА КОНТУР С ТОКОМ. ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА
- ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- ЭФФЕКТ ХОЛЛА
- § 21. РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
- § 22. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ; ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА. ВРАЩАЮЩИИСЯ ВИТОК В МАГНИТНОМ ПОЛЕ
- РАМКА В МАГНИТНОМ ПОЛЕ
- ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА
- § 23. ЯВЛЕНИЯ САМОИНДУКЦИИ И ВЗАИМОИНДУКЦИИ. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ВИХРЕВЫЕ ТОКИ
- ИНДУКТИВНОСТЬ СОЛЕНОИДА
- РАСЧЕТ ИНДУКЦИОННЫХ ТОКОВ
- ВЗАИМНАЯ ИНДУКЦИЯ
- ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
- ТОКИ ФУКО
- § 24. ТОК СМЕЩЕНИЯ И ЕГО МАГНИТНОЕ ПОЛЕ; ТЕОРИЯ МАКСВЕЛЛА
- § 25. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ. ДИАМАГНЕТИЗМ; ПАРАМАГНИТНЫЕ И ФЕРРОМАГНИТНЫЕ ВЕЩЕСТВА
- НАМАГНИЧЕННОСТЬ
- МАГНИТНЫЕ СВОЙСТВА АТОМОВ И МОЛЕКУЛ
- ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ
- ФЕРРОМАГНЕТИКИ
- ПАРАМАГНИТНЫЙ РЕЗОНАНС
- § 26. МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕ
- Глава 4. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 27. КОЛЕБАТЕЛЬНЫЙ КОНТУР. НЕЗАТУХАЮЩИЕ И ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 28. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ; ЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС
- § 29. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- УРАВНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ИЗЛУЧЕНИЕ ВОЛНЫ ЭЛЕКТРОНОМ
- ЧЕРЕНКОВСКОЕ ИЗЛУЧЕНИЕ
- Часть IV. ОПТИКА И ФИЗИКА АТОМА
- § 1. ВОЛНОВАЯ (ЭЛЕКТРОМАГНИТНАЯ) И КОРПУСКУЛЯРНАЯ (ФОТОННАЯ) ТЕОРИИ СВЕТА
- СПЕКТРАЛЬНЫЙ СОСТАВ ИЗЛУЧЕНИЯ
- ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ
- ИДЕАЛИЗАЦИЯ СВЕТОВОЙ ВОЛНЫ
- § 2. ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ВЕЛИЧИНЫ. ДАВЛЕНИЕ СВЕТА
- § 3. РАСПРОСТРАНЕНИЕ, ОТРАЖЕНИЕ, ПРЕЛОМЛЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА. ДИСПЕРСИЯ. РАССЕЯНИЕ СВЕТА
- СБЕТ НА ГРАНИЦЕ ДВУХ СРЕД
- СВЕТ И ЦВЕТ
- ДИСПЕРСИЯ СВЕТА
- РАССЕЯНИЕ СВЕТА
- § 4. ИНТЕРФЕРЕНЦИЯ СВЕТА; КОГЕРЕНТНОСТЬ СВЕТОВЫХ ЛУЧЕЙ. ИНТЕРФЕРОМЕТРЫ
- § 5. ДИФРАКЦИЯ СВЕТА; ДИФРАКЦИОННЫЙ СПЕКТР
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ ПРЯМОЛИНЕЙНОЙ ТОНКОЙ ЩЕЛИ
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ НЕСКОЛЬКИХ ЩЕЛЕЙ
- ДИФРАКЦИОННАЯ РЕШЕТКА
- § 6. РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТА
- ПОЛЯРИЗОВАННЫЙ СВЕТ
- СПОСОБЫ ПОЛУЧЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ОПТИЧЕСКАЯ АНИЗОТРОПИЯ
- § 7. ЛИНЗЫ; ИХ ОПТИЧЕСКАЯ СИЛА. АБЕРРАЦИИ. ДИАФРАГМЫ В ОПТИЧЕСКИХ ПРИБОРАХ
- ТОЛСТЫЕ ЛИНЗЫ. АБЕРРАЦИИ
- § 8. ПОНЯТИЕ О ГОЛОГРАФИИ
- Глава 2. ФИЗИКА АТОМОВ И МОЛЕКУЛ. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
- § 9. СТРОЕНИЕ АТОМА. ОПЫТЫ РЕЗЕРФОРДА, ФРАНКА И ГЕРЦА. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ АТОМА ВОДОРОДА
- ОПЫТ ФРАНКА И ГЕРЦА
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- ТЕОРИЯ АТОМА ВОДОРОДА
- § 10. КОРПУСКУЛЯРНО-ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ. ФОРМУЛА ДЕ БРОЙЛЯ. ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- ЭФФЕКТ КОМПТОНА
- ФОТОН И ЭЛЕКТРОМАГНИТНАЯ ВОЛНА
- ФОРМУЛА ДЕ БРОЙЛЯ
- ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- § 11. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ТЕОРИИ. УРАВНЕНИЕ ШРЕДИНГЕРА. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА
- УРАВНЕНИЕ ШРЕДИНГЕРА
- РЕШЕНИЯ УРАВНЕНИЯ ШРЕДИНГЕРА
- СВОБОДНЫЙ ЭЛЕКТРОН
- ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
- ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ
- АТОМ ВОДОРОДА. КВАНТОВЫЕ ЧИСЛА
- СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- § 12. ЧАСТИЦЫ И ФИЗИЧЕСКИЕ СИСТЕМЫ. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО СОСТОЯНИЯМ. ПОНЯТИЕ ТЕМПЕРАТУРЫ
- РОЛЬ ТЕПЛОВОГО ДВИЖЕНИЯ ЧАСТИЦ
- ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПО СОСТОЯНИЯМ
- ТЕМПЕРАТУРА
- ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИСТЕМЫ
- РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ
- § 13. ВЗАИМОДЕЙСТВИЕ АТОМОВ И МОЛЕКУЛ. ЭНЕРГИЯ СВЯЗИ АТОМОВ
- ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ
- ИОННАЯ СВЯЗЬ
- РОЛЬ ЭЛЕКТРОННОГО ГАЗА В МЕТАЛЛАХ
- Глава 3. ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ ЭНЕРГИИ АТОМАМИ И МОЛЕКУЛАМИ
- § 14. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ ИЗЛУЧЕНИЯ; СПОСОБЫ ВОЗБУЖДЕНИЯ
- СТРУКТУРА ЭЛЕКТРОННОЙ ОБОЛОЧКИ
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- СПЕКТРЫ ИЗЛУЧЕНИЯ МОЛЕКУЛ
- КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
- § 15. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
- ФОРМУЛА ПЛАНКА
- ЗАКОНЫ ИЗЛУЧЕНИЯ ЧЕРНОГО ТЕЛА
- ПРИМЕНЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- § 16. РЕНТГЕНОВСКИЕ ЛУЧИ. ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ЭЛЕМЕНТОВ
- ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР
- ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
- ДОЗИМЕТРИЯ
- § 17. ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕ
- ПРИРОДА ЛЮМИНЕСЦЕНЦИИ
- ХАРАКТЕРИСТИКИ ЛЮМИНЕСЦИРУЮЩИХ ВЕЩЕСТВ
- ГАШЕНИЕ ЛЮМИНЕСЦЕНЦИИ
- ПРИМЕНЕНИЯ ЛЮМИНЕСЦЕНЦИИ
- § 18. ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ. ЛАЗЕРЫ
- ЛАЗЕРЫ
- ПРЕИМУЩЕСТВА ЛАЗЕРОВ
- ПРИМЕНЕНИЕ ЛАЗЕРОВ
- Глава 4. АТОМНЫЕ ЯДРА И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 19. ОСНОВНЫЕ СВОЙСТВА АТОМНЫХ ЯДЕР
- РАДИОАКТИВНОСТЬ
- ВНУТРИЯДЕРНЫЕ СИЛЫ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕР
- МЕХАНИЧЕСКИЙ МОМЕНТ ЯДРА
- МАГНИТНЫЕ МОМЕНТЫ ЯДЕР
- ЭЛЕКТРИЧЕСКИЕ МОМЕНТЫ ЯДЕР
- СПЕКТР ВОЗБУЖДЕННЫХ СОСТОЯНИЙ
- § 20. МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О СТРУКТУРЕ ЯДЕР
- КАПЕЛЬНАЯ МОДЕЛЬ ЯДРА
- ОБОЛОЧЕЧНАЯ МОДЕЛЬ
- ОБОБЩЕННАЯ МОДЕЛЬ
- ОПТИЧЕСКАЯ МОДЕЛЬ
- УСЛОВИЕ СТАБИЛЬНОСТИ
- § 21. РАДИОАКТИВНЫЕ ЯДРА И ИХ ИЗЛУЧЕНИЯ
- СЕМЕЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ
- ВЗАИМОДЕЙСТВИЯ ЯДЕРНЫХ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ
- БЕТА-РАСПАД ЯДЕР
- ЭНЕРГИЯ СВЯЗИ ЯДЕР
- ИЗОМЕРЫ
- § 22. ЯДЕРНЫЕ РЕАКЦИИ ДЕЛЕНИЯ И СИНТЕЗА. ТЕРМОЯДЕРНЫЕ РЕАКЦИИ
- БОМБАРДИРОВКА ЯДЕР ЧАСТИЦАМИ
- ЭФФЕКТИВНЫЕ СЕЧЕНИЯ РЕАКЦИЙ
- ЯДЕРНЫЕ РЕАКТОРЫ
- ЯДЕРНЫЙ СИНТЕЗ
- § 23. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- РАСПАДЫ ЧАСТИЦ
- ВИДЫ ВЗАИМОДЕЙСТВИЯ
- ЗАКЛЮЧЕНИЕ
- § 1. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ. СВЯЗЬ МЕЖДУ СПОСОБАМИ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН И ФОРМУЛИРОВКАМИ ЗАКОНОВ ФИЗИКИ
- § 2. О ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ЗАКОНЫ СОХРАНЕНИЯ, ПРЕВРАЩЕНИЯ И ПЕРЕРАСПРЕДЕЛЕНИЯ ЭНЕРГИИ В ФИЗИЧЕСКИХ СИСТЕМАХ
- § 4. О ВАРИАЦИОННЫХ ПРИНЦИПАХ ФИЗИКИ
- § 5. СТАТИСТИЧЕСКИЕ ЗАКОНЫ И ФЛУКТУАЦИИ
- § 6. О ДУАЛИЗМЕ В ФИЗИКЕ

