Как найти скорость перемещения в момент времени

Была ли эта статья полезной?

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Формула перемещения

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

v = v₀ ± at

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

t₁ = t – t₂

Когда тело тормозит, через некоторое время t₁ оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

0 = v₀₁ – at₁

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

t₂ = t – t₁

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

v = at₂

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

s = |s₁ – s₂|

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

l = s₁ + s₂

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с². Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

v₀₂ = v₀₁ + a₁t₁ = a₁t₁ (так как v₀₁ = 0)

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с^2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с². Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Алиса Никитина | Просмотров: 25.4k

Мгновенная и средняя скорость

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.

Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения ” open=” υ = ∆ r ∆ t ; ” open=” υ ↑ ↑ ∆ r .

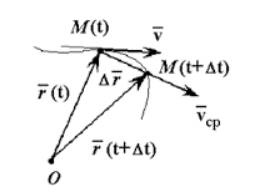
Рисунок 1 . Средняя скорость сонаправлена перемещению

Модуль средней скорости по пути равняется ” open=” υ = S ∆ t .

Мгновенная скорость точки. Формулы

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Мгновенной скоростью называют предел, к которому стремится средняя скорость ” open=” υ при стремлении промежутка времени ∆ t к 0 :

υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .

Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .

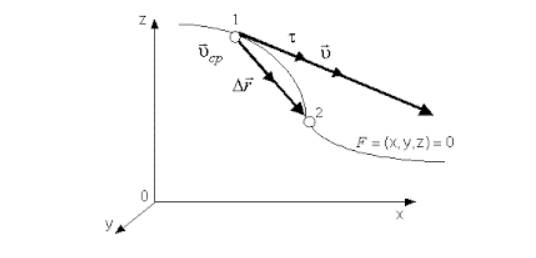
Рисунок 2 . Вектор мгновенной скорости υ

Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:

υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .

Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:

υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .

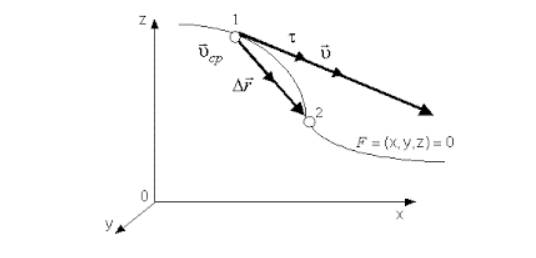
Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат

При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:

υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t

Дан закон прямолинейного движения точки x ( t ) = 0 , 15 t 2 – 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

υ ( t ) = x ˙ ( t ) = 0 . 3 t – 2 ; υ ( 10 ) = 0 . 3 × 10 – 2 = 1 м / с .

Ответ: 1 м / с .

Движение материальной точки задается уравнением x = 4 t – 0 , 05 t 2 . Вычислить момент времени t о с т , когда точка прекратит движение, и ее среднюю путевую скорость ” open=” υ .

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ ( t ) = x ˙ ( t ) = 4 – 0 , 1 t .

4 – 0 , 1 t = 0 ; t о с т = 40 с ; υ 0 = υ ( 0 ) = 4 ; ” open=” υ = ∆ υ ∆ t = 0 – 4 40 – 0 = 0 , 1 м / с .

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с .

Мгновенная скорость

Средняя оценка: 4.3

Всего получено оценок: 225.

Средняя оценка: 4.3

Всего получено оценок: 225.

Большинство движений в природе являются неравномерными. При описании таких движений большое значение имеет параметр «мгновенная скорость». Рассмотрим его подробнее.

Скорость при неравномерном движении

Скорость – величина, показывающая, какое расстояние проходит материальная точка за единицу времени:

Рис. 1. Скорость равномерного прямолинейного движения.

Однако, для определения положения материальной точки в любой момент времени, во многих случаях эту формулу применять нельзя.

В самом деле, если провести опыт, можно видеть, что на Земле предмет падает с высоты 20м за 2.02с. Откуда следует, что скорость падения составляет:

Выходит, что через полсекунды после начала падения предмет окажется на 5м ниже, чем исходная точка, через секунду – на 9.9м ниже.

Однако, проведя реальное измерение, можно убедиться, что это совсем не так. За первую секунду предмет пройдет только 4.9м. А за первые полсекунды – всего лишь 1.23м ! Если же высота падения будет больше, то за три секунды путь составит не 29.7м, как следует из формулы, а больше 40м !

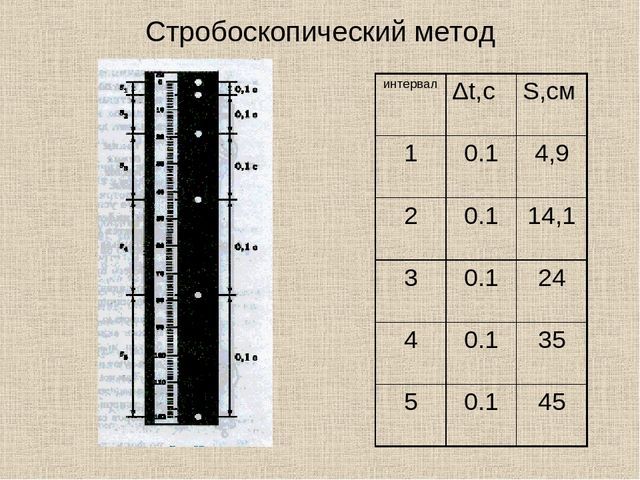Рис. 2. Стробоскопическое фото свободного падения.

Причина такого расхождения с расчетом состоит в том, что предмет под действием тяготения Земли движется неравномерно, постоянно изменяя скорость. И на каком бы участке мы не измерили его скорость – полученное значение будет различно, и его невозможно будет использовать в расчетах и уравнениях для других участков.

Свести неравномерное движение к равномерному невозможно.

Мгновенная скорость

Описанное затруднение можно разрешить, если учесть, что движение – процесс непрерывный. Ни координаты точки, ни ее скорость не могут изменяться скачками. Во время движения точка проходит все бесчисленное множество координат пути, на всем пути скорость ее непрерывно изменяется в некотором диапазоне, и при этом, чем меньше рассматриваемый отрезок времени, тем меньше будет изменение координаты и скорости.

Рассмотрим падение предмета, начиная с конца первой секунды. В этот момент координата будет равна 4.905м. Отметим новую координату падающего предмета через небольшое время, и вычислим скорость:

Как рассчитать мгновенную скорость, формулу мгновенной скорости

Мгновенная скорость сообщает нам о движении частицы в определенный момент времени в любом месте на ее пути.

Мгновенная скорость принимается за предел средней скорости при стремлении времени к нулю. Вычислять V_инст мы можем использовать график смещения-времени / формулу мгновенной скорости. т.е. производная смещения (s) по времени (t), взятая.

Чтобы узнать, как рассчитать мгновенную скорость объекта, нам нужно выполнить следующие действия. . Давайте посмотрим на это на примере.

Рассмотрим уравнение скорости в терминах положения / смещения.

Вычислять мгновенная скорость, мы должны рассмотреть уравнение это говорит нам о его должность ‘s’ в определенный время ‘t’. Это означает, что уравнение должно содержать переменную ‘s‘с одной стороны и’t‘ с другой стороны,

s = -2т 2 + 10т +5 при t = 2 секунды.

В этом уравнении переменными являются:

Смещение = s, измеряется в метрах.

Время = t, измеряется в секундах.

Рассмотрим производную данного уравнения.

Чтобы найти производную данного уравнения перемещения, дифференцировать функцию по времени,

ds / dt = – (2) 2т (2-1) + (1) 10 т 1 – 1 + (0) 5 т 0

ds / dt = -4т 1 + 10т 0

ds / dt = -4t + 10

Подставьте данное значение «t» в уравнение производной, чтобы найти мгновенную скорость.

Найдите мгновенная скорость при t = 2 подставить “2” для t в производной ds / dt = -4t + 10. Тогда мы можем решить уравнение

ds / dt = -4 (2) + 10

ds / dt = -8 + 10

ds / dt = -2 метра в секунду

Здесь «метры / секунда» – это единица измерения мгновенной скорости в системе СИ.

Как рассчитать Instantaneo скорость нас из графика

Мгновенная скорость в любой конкретный момент времени определяется наклоном касательной, проведенной к графику положения-времени в этой точке.

• Постройте график расстояние против времени.
• Отметьте точку, в которой вам нужно найти мгновенную скорость, скажем A.
• Определите точку на графике, соответствующую времени t₁ и t₂.
• Вычислить v_{средний} и проведем касательную в точке A.
• На графике v_инст в точке A находится по касательной, проведенной в этой точке

• Чем длиннее тангенс, тем точнее будут значения.
• На показанном изображении Синяя линия это график зависимости положения от времени, А Красная линия – приблизительный наклон линии при t = 2.5 секунды.

• Если мы продолжаем выбирать точки, которые все ближе и ближе друг к другу, линия начнет приближаться к наклону линии, касательной к одной точке.
• Если мы возьмем предел функции в этой точке, мы получим значение наклона касательной в этой точке.
• Расстояние составляет примерно 140 м, а временной интервал – 4.3 с. Следовательно, приблизительный уклон составляет 32.55 м / с.

Как рассчитать мгновенную скорость по графику положения-времени.

Для вычисления мгновенной скорости по графику положения-времени.

Постройте график зависимости смещения от времени.

• Используйте оси X и Y для представления время и перемещение.
• Затем нанесите на график значения времени и смещения.

Выберите любые две точки на графике st.

• Линия смещения содержит точки (3,6) и (5,8).
• В этом примере, если мы хотим найти наклон в точке (3,6), мы можем установить А = (3,6) и B=(5,8)

Найдите наклон линии, соединяющей две точки, т. Е. Между точками A и B.

Найдите среднюю скорость между этими двумя временными интервалами, т. Е.

где K – наклон между двумя точками.

Здесь наклон между A и B равен:

Повторите несколько раз, чтобы найти уклон, перемещая B ближе к A.

• Продолжайте выбирать точки ближе друг к другу; затем он начнет приближаться к наклону касательной.
• Если мы рассмотрим предел функции в этой точке, мы получим значение наклона в этой точке.
• Здесь мы можем использовать точки (4,7.7), (3.5, 6.90) и (3.25, 6.49) для B и исходную точку (3,6) для A.

Вычислите наклон для бесконечно малого отрезка касательной.

В этом примере, когда мы приближаем B к A, мы получаем значения 1.7, 1.8 и 1.96 для K. Поскольку эти числа примерно равны 2, можно сказать, что 2 – наклон А.

Здесь, мгновенная скорость 2 м / с.

Формула мгновенной скорости

С математической точки зрения мы можем написать формула мгновенной скорости в виде,

Здесь, ds / dt – это производная смещения (с) по времени (t).

Приведенные выше производная имеет конечное значение когда и знаменатель, и числитель стремятся к нулю.

Расчет формулы мгновенной скорости

Используя вычисления, всегда можно вычислить скорость объекта в любой момент на его пути. Это называется мгновенной скоростью. и задается уравнением v = ds / dt .

Мгновенная скорость = предел, поскольку изменение во времени приближается к нулю (изменение положения / изменение во времени) = производная смещения по времени

Формула средней и мгновенной скорости

	Формула	Символ	Определение
Средняя скорость		sf = Окончательный смещение si = Начальное смещение tf = Последний раз ti = Начальное время	Средняя скорость is общее расстояние деленное на общее затраченное время.
Мгновенная скорость			Скорость при любом момент времени.

Формула мгновенной угловой скорости

мгновенная угловая скорость скорость, с которой частица движется по круговой траектории в определенный момент времени.

мгновенная угловая скорость вращающегося объекта определяется выражением

dθ/dt = производная углового положения θ по времени, найденное предельным переходом Δ t → 0 в средняя угловая скорость.

направление угловой скорости на круговой траектории – вдоль оси вращения и указывает от вас на вращающееся тело по часовой стрелке и к вам для тела, вращающегося против часовой стрелки. В математике это обычно описывается правило правой руки.

Формула мгновенной скорости и скорости

Формула мгновенной скорости

Формула мгновенной скорости

Разница между мгновенной скоростью и мгновенной скоростью.

Мгновенная скорость	Мгновенная скорость
Это скорость движущейся частицы в определенный момент t.	Вход в музей Мадам Тюссо мера скорости частицы в определенный момент t.
Мгновенная скорость определяет, насколько быстро и в каком направлении движется объект.	Мгновенная скорость измеряет, насколько быстро частица движется.
Количество векторов	Скалярная величина

Определение и формула мгновенной скорости

Определение мгновенной скорости

Мгновенная скорость описывается как скорость движущегося объекта. Мы можем найти его, используя среднюю скорость, но мы должны сузить время, чтобы приблизиться к нулю.

Итого можно сказать, что мгновенная скорость – это скорость движущейся частицы в определенный момент времени.

Формула мгновенной скорости

Для любого уравнения движения s(t), для мгновенная скорость когда t приближается к нулю, мы можем записать формула в виде,

Мгновенная скорость формула предела

Мгновенная скорость любого объекта – это предел средней скорости, когда время приближается к нулю..

Вставьте значения t₁= t и t₂ = t + Δt в уравнение для средней скорости и переходя к пределу при Δt → 0, находим формула предела мгновенной скорости

Как найти мгновенную скорость на графике

Мгновенная скорость равна наклону касательной на графике положение-время.

Мгновенно s Интерпретация скорости из графика st

• Мгновенная скорость равна наклону касательной на графике положение-время.
• Интерпретация мгновенной скорости по графику st

• Наклон фиолетовой линии (касательной) на графике смещения v / s дает мгновенную скорость.
• Если фиолетовая линия образует угол с положительной осью абсцисс.

V_inst = наклон фиолетовой линии = tanθ

Как найти мгновенную скорость из средней скорости

Для того, чтобы найти мгновенная скорость в точке, мы должны сначала найти среднюю скорость в этой точке.

Вы можете найти мгновенную скорость при t = a с помощью вычисление средней скорости графика зависимости положения от времени путем взятия меньшего и большего приращения точки, в которой вы хотите определить V _{inst .}

Пример мгновенной скорости

Во время езды на велосипеде велосипедист меняет свою скорость в зависимости от расстояния и времени, которое он проходит.

Если мы хотим найти скорость в одной конкретной точке, мы должны использовать мгновенную скорость.

Покажи нам пример,

а). Определить мгновенную скорость частицы, движущейся по прямому пути за t = 2 секунды, с функцией положения «s», определенной как 4t² + 2t + 3?

Решение:

Данный с = 4т² + 2т + 3

Дифференцируя данную функцию по времени, мы вычисляем мгновенную скорость следующим образом:

Подставляя значение t = 2, мы получаем мгновенную скорость как,

Подставляя функцию s,

Таким образом, мгновенная скорость для вышеуказанной функции составляет 18 м / с.

Проблема мгновенной скорости

Некоторые проблемы с мгновенной скоростью,

Проблема 1:

Движение тележки задается функцией s = 3t 2 + 10t + 5. Вычислите его мгновенную скорость в момент времени t = 4 с.

Решение:

Данная функция s = 3t 2 + 10т + 5.

Продифференцируя указанную выше функцию по времени, получим

Подставляя функцию s,

[v_ = v (t) = 6t + 10]

Подставляя значение t = 4 с, мы получаем мгновенную скорость как,

Для данной функции мгновенная скорость составляет 34 м / с.

Проблема 2:

Выстреленная пуля движется по прямой траектории, и ее уравнение движения имеет вид S (t) = 3t + 5t. 2 . Так, например, если он летит за 12 секунд до удара, найдите мгновенную скорость при t = 7 с.

Решение: Мы знаем уравнение движения:

Проблема 3:

Объект выпускается с определенной высоты, чтобы он мог свободно падать под действием силы тяжести. Уравнение движения для перемещения s (t) = 5.1 т. 2 . Какой будет мгновенная скорость объекта в момент времени t = 6 с после выпуска?

Решение:

Мгновенная скорость при t = 6 с

Проблема 4:

Найдите скорость при t = 2, учитывая уравнение перемещения s = 3t 3 – 3т 2 + 2т + 7.

Решение:

Это похоже на предыдущие задачи, за исключением того, что они дали кубическое уравнение вместо квадратного уравнения, чтобы решить его таким же образом.

s (t) = 3t 3 – 3т 2 + 2т + 7.

Мгновенная скорость при t = 7 с

Проблема 5:

Положение человека, движущегося по прямой, определяется выражением s (t) = 7t. 2 + 3t + 19, где t – время (секунды). Найдите уравнение для мгновенной скорости v (t) частицы в момент времени t.

Решение:

Дано: s (t) = 7t 2 + 3т + 19

v_инст = v (t) = (14t + 3) м / с – уравнение для мгновенной скорости.

Предположим, что если принять t = 3s, то

Проблема 6:

Движение автомобиля описывается уравнением движения s = gt 2 + b, где b = 20 м и g = 12 м. Следовательно, найдите мгновенную скорость при t = 4 с.

Решение:

Здесь g = 12 и t = 4s,

v (4) = [2 x 12 x 4] = 96 м / с.

v (т) = 96 м / с.

Проблема 7:

Стол, упавший со здания 1145 футов, имеет высоту (в футах) над землей, определяемую как s (t) = 1145-12 т. 2 . Затем вычислите мгновенную скорость стола на 3 с?

Решение:

Мгновенная скорость при t = 3 с составляет -72 м / с.

Проблема 8:

Функция положения частиц определяется выражением s = (3t 2 )_i – (4т)_k + 2. какова его мгновенная скорость при t = 2? Каково его мгновенное ускорение как функция времени?

Решение:

Чтобы вычислить мгновенное ускорение как функцию времени

дифференцируя уравнение 1 по t, получаем

Проблема 9:

Положение насекомого определяется как s = 44 + 20t – 3t. 3 , где t в секундах, а s в метрах .

а. Найдите среднюю скорость объекта между t = 0 и t = 4. s.

б. В какое время между 0 и 4 мгновенная скорость равна нулю.

решение:

Для расчета средней скорости

Чтобы найти время, при котором мгновенная скорость равна нулю.

Проблема 10:

Частица движется с функцией смещения s = t 2 + 3 .

Найдите положение при t = 2.

Найдите среднюю скорость от t = 2 до t = 3.

Найти его мгновенную скорость при t = 2 .

Решение:

Чтобы найти позицию при t = 2

с (2) = 7

Для того, чтобы найти Средняя скорость.

Чтобы найти мгновенную скорость

При t = 2 с

Мгновенная скорость в зависимости от средней скорости

Мгновенная скорость	Средняя скорость
мгновенная скорость – средняя скорость между двумя точками.	Средняя скорость это соотношение изменения дистасть относительно времени за период.
Мгновенная скорость рассказывает о движении между двумя точками на пройденном пути.	Средняя скорость не дает информации о движении между точками. Путь может быть прямым / изогнутым, а движение может быть постоянным / переменным.
Мгновенная скорость равен наклону касательной к смещение (с) в зависимости от графика времени.	Он равен наклону секущая линия of граф st.
вектор	вектор

Как найти мгновенная скорость без исчисления

Wмы можем найти мгновенную скорость приближением по график зависимости смещения от времени без исчисления в определенной точке. Нам нужно провести касательную в точке вдоль изогнутой линии и оценить наклон, где вам нужно найти мгновенную скорость.

Как рассчитать мгновенную скорость и мгновенное ускорение

	Мгновенная скорость	Мгновенное ускорение
Из формулы	Для расчета мгновенной скорости, возьмем предел изменения расстояния по времени, когда время приближается к нулю. т. е. взяв первая производная функции смещения.	к рассчитать мгновенное ускорение, принять предел изменения скорости по времени, когда изменение во времени приближается к нулю. т.е. взяв вторая производная функции смещения.
Из графика	Равно наклон касательной к графику st.	Равно наклон касательной графика vt.

11 задачи:

Пуля, выпущенная в космос, движется по прямой траектории, и ее уравнение движения имеет вид s (t) = 2t + 4t 2 . Если он движется в течение 12 секунд до удара, найдите мгновенную скорость и мгновенное ускорение в момент времени t = 3 секунды.

Решение: Мы знаем уравнение движения: s (t) = 2t + 4t 2

Как найти мгновенную скорость и скорость

Мгновенная скорость задается как величина мгновенной скорости.

Если известно смещение как функция времени, мы можем узнать мгновенную скорость в любое время.

Давайте разберемся в этом на примере.

12 задачи:

Уравнение движения s (t) = 3t 3

Рассмотрим t = 2s

Почему можно рассчитать мгновенную скорость по кинематическим формулам только при постоянном ускорении

Уравнения кинематики можно использовать только при постоянном ускорении объекта.

В случае переменные ускорения, Уравнения кинематики будут разными в зависимости от функции, которую принимает ускорение; в то время; мы должны использовать Комплексный подход вычислять мгновенная скорость. Что будет немного сложно.

Почему при вычислении мгновенной скорости мы берем небольшие промежутки времени. Как он дает скорость в этот момент, если мы рассчитываем ее за определенный промежуток времени?

мгновенная скорость дан кем-то ,

Чем меньше значение «t», Тем точнее будет наклон касательной, т. е. мгновенная скорость.

Когда ты хочешь рассчитать скорость в определенное время вам нужно сначала рассчитать средние скорости взяв небольшие промежутки времени. Если эти средние скорости дают одно и то же значение, тогда это будет требуемый мгновенная скорость.

Различаются ли скорость и мгновенная скорость?

Мгновенная скорость отличается от скорости.

Скорость обычно известен как скорость изменения положения во времени. Напротив, в мгновенная скорость, временной интервал сужается, чтобы приблизиться к нулю, чтобы получить скорость в конкретный момент времени.

Например,

Частица движение по кругу имеет нулевые смещения, и требуется знать скорость частицы. В этом случае мы можем вычислить мгновенную скорость, потому что она имеет тангенциальная скорость в любой момент времени.

Что такое мгновенная скорость на реальных примерах

Реальные примеры мгновенной скорости

Если мы рассмотрим пример мяча для сквоша, мяч возвращается в исходную точку; в это время полное смещение и средняя скорость будут равны нулю. В таких случаях движение рассчитывается по формуле мгновенная скорость.

• Спидометр автомобиля дает информацию о мгновенная скорость / скорость средство передвижения. Он показывает скорость в определенный момент времени.

Во время гонки фотографы делают снимки бегунов, их средняя скорость не меняется, но меняется их мгновенная скорость, зафиксированная на «снимках». Так что это будет пример мгновенной скорости.

• Если вы находитесь рядом с магазином, и перед вами проехал автомобиль на отметке «t«Во-вторых, и вы начинаете думать о его скорости на конкретном время, здесь вы имели бы в виду мгновенная скорость транспортного средства.

Часто задаваемые вопросы | FAQs

Является ли мгновенная скорость вектором

Мгновенная скорость – это векторная величина.

Мгновенная скорость – это вектор, потому что он имеет как величину, так и направление. Он показывает как скорость (относится к величине), так и направление. участникале Имеет размер LT -1 Мы можем определить это, взяв наклон графика расстояние-время..

Как найти мгновенную скорость только с графиком положения и времени и без заданного уравнения

Мы можем определить мгновенную скорость, взяв наклон графика положения-времени.

• Постройте график смещения во времени.
• Выберите точку A и другую точку B, которая находится рядом с точкой A на линии.
• Найдите угол наклона между A и B, рассчитайте несколько раз, перемещая A ближе к B.
• Рассчитайте наклон для бесконечно малого интервала на прямой.
• Полученный наклон представляет собой мгновенную скорость.

Можно ли мгновенно изменить скорость

Невозможно вызвать мгновенное изменение скорости, так как для этого потребуется бесконечное ускорение.

Как правило, ускорение является результатом F = ma

а скорость является результатом ускорения (от интегрирования). Если изменение скорости является ступенчатой ​​функцией и когда время приближается к нулю, потребуется бесконечное ускорение и сила, чтобы мгновенно изменить скорость массы.

Как я могу рассчитать смещение, если ускорение является функцией мгновенной скорости Задана начальная скорость

Мы можем вычислить смещение двумя способами, когда задана начальная скорость.

От происхождения

Здесь ускорение является функцией мгновенной скорости,

Начальная скорость

Интегрируя,

Используя эту форму, вы можете получить ds смещения.

Из формулы

Используя приведенное ниже кинематическое уравнение, мы можем найти смещение,

Что такое средний и мгновенная скорость

Средняя скорость и мгновенная скорость выражаются следующим образом:

Средняя скорость	Мгновенная скорость
Средняя скорость для определенного временного интервала – это полное смещение, деленное на общее время.	И временной интервал, и смещение в какой-то момент приближаются к нулю. Но предел производной смещения по общему интервалу времени отличен от нуля и называется мгновенной скоростью.
Средняя скорость это скорость всего пути в движении	а мгновенная скорость скорость частицы в определенный момент времени
v avg = s/t	v inst = ds/dt

Мгновенное ускорение перпендикулярно мгновенной скорости

Мгновенное ускорение тела всегда перпендикулярно мгновенной скорости.

При круговом движении мгновенное ускорение тела всегда перпендикулярно мгновенной скорости, и это ускорение называется центростремительным ускорением. Скорость остается неизменной; только направление меняется, поскольку перпендикулярное ускорение изменяет траекторию тела.

Последние выпуски передовой науки и исследований

[spoiler title=”источники:”]

http://obrazovaka.ru/fizika/mgnovennaya-skorost-formula.html

http://ru.lambdageeks.com/how-to-calculate-instantaneous-velocity-formula/

[/spoiler]

В ситуации, когда координаты изменяют свое положение относительно оси, следовательно, их материальная точка будет находится в процессе движения.

Средняя скорость — это величина векторного типа, которая имеет определенное числовое равенство относительно перемещения совершаемого  в конкретную единицу времени, и направлена совместно я с векторным  перемещением.

Средняя скорость – довольно простое понятие в разделе кинематика.

[v_{mathrm{cp}}=frac{S}{t}]

Основные моменты, на которые следует уделить внимание при определении средней скорости:

• Необходимое время, которое учитывается, когда тело в процессе движения может делать кратковременные остановки;
• Определение правильной величины средней скорость тела, которое начинает движение в пункте А и оканчивает его в пункте В. Но в процессе движения, может повернуть несколько раз обратно, а затем снова продолжает движение в заданном направлении, двигаясь в пункт В.

Модуль для определения средней скорости движения вычисляется по следующей формуле: V=s/t.

Мгновенная скорость, как правило, характеризует заданное движение точки в конкретный и определенный момент времени.

Для любой категории характерно бесконечное количество точек. Потому что каждый временной интервал включает в себя бесконечное количество мгновений.

Когда сам временной интервал стремится к нулевому значению, то он автоматически преобразуется в мгновение.

Стоит отметить, что мгновенная скорость – это величина, которая изображена как вектор. Она равняется отношению движения к временному интервалу. А именно: промежуток времени, за который данное перемещение происходит, при условии, что временной интервал стремится к нулевому значению.

Временной интервал движения тела –  это всегда скляр с положительным значением. Поэтому мгновенная скорость и ее векторное значение,  всегда сонаправлено с перемещением, которое имеет значение стремящееся к нулю.

Направление и перемещение действия средней и мгновенной скорости относительно координатной оси

Средняя скорость всегда направлена вместе с перемещением:

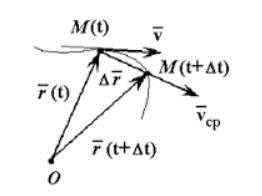
Для мгновенной скорости характерно движение в конкретный момент времени.

Направление векторной скорости, которая обозначается как: υ расположено по касательной, относительно криволинейной траектории.

Так как непрерывное малое перемещение однозначно совпадает с бесконечно малым элементом траектории.

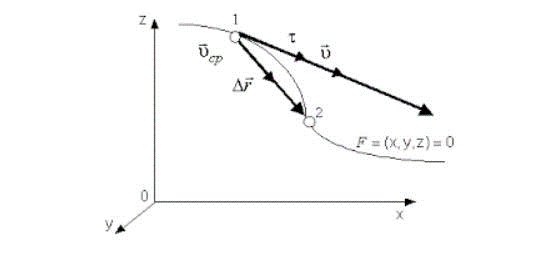
Примеры решения задач по определению мгновенной и средней скорости

Пример №1:

Имеет ли способность мгновенная скорость, изменять свое значение только относительно направления, при этом не меняя модульную величину.

Используя основные термины и формулы, решим данную задачу. При решении необходимо рассмотреть пример:

• Движение тела происходит по криволинейной траектории. На ней необходимо обозначить начальный и конечный пункты, а именно: точки А и В.
• Далее нужно обозначить основное направление мгновенной скорости в заданных ранее точках.
• Следует помнить, что мгновенная скорость имеет направление относительно касательной по траектории.
• Расстояние и скорость имеют одинаковые значения  по модулю и, следовательно, равны 5 м/с.

[left|vec{V}_{A}right|=left|vec{V}_{B}right|=5 frac{м}{c}]

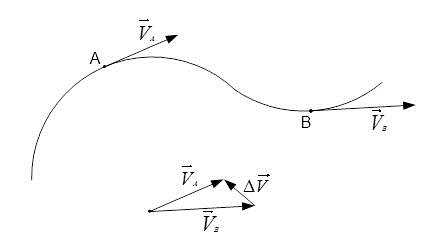
Следующее равенство вида: [vec{V}_{A}=vec{V}_{B}] будет неверным. Так как скорость – является векторной величиной. Поэтому очень важно задать не только числовое значение, но направление по которому будет осуществляться движение.

В случае, когда [vec{V}_{A}=vec{V}_{B}] можно составить равенство следующего вида:[vec{V}_{A}-vec{V}_{B}=0] однако определив вектор разности значений [Delta vec{V}], можно сделать вывод, что его значение не равно нулевому.

Следовательно, [vec{V}_{A} neq vec{V}_{B}], другими словами мгновенная скорость может быть равна нулевому значению и быть равной по модулю. Однако, при этом различаться по основному направлению движения.

Пример №2:

Возможно ли изменение по модульному значению мгновенной скорости, но при этом направление остается неизменным.

Алгоритм решения:

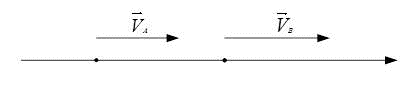
Рассмотрев рисунок, который приведен выше, можно сделать вывод, что:

• в точке А и в точке В направление движения мгновенной скорости одинаково;
• рассматриваемое тело, которое осуществляет   движение, делает это   с равным ускорением, следовательно:

[vec{V}_{A}=vec{V}_{B}]

В данной статьи изложены мысли, которые возникали при решении задач с сайта “Решу ЕГЭ” в разделе – https://phys-ege.sdamgia.ru/test?theme=204. Рисунки взяты оттуда же.

1. Общий подход

Анализ и использование данного графика базируется на формуле перемещения тела S, м:

Как видно из формулы площадь под графиком равна перемещению тела. Например, тело с 1 по 2 секунду на графике, представленном на рис. 1 прошло S = V * t = 2м/с * (2с – 1с) = 2м/с *1с = 2м

2. Чуть посложнее

Если мы захотим найти перемещение тела с начала движения t = 0c до 4-ой секунды движения тела согласно графику на рис. 2, то нам необходимо найти сумму площадей трех геометрических фигур: с 0с по 1с – треугольник, с 1с по 2с прямоугольник, со 2с по 4с – трапеция.

S треугольника = (1/2) * длину высоты треугольника * длину сторону треугольника, к которой проведена высота =
=(1/2) * 2м/с * (1с – 0с) = 1/2 * 2м/с * 1с = 1м
S прямоугольника мы находили в начале статьи = 2м
S трапеции = (1/2) * сумму оснований трапеции * высоту трапеции =
=(1/2) * (2м/с + 6м/с) * (4с – 2с) = (1/2) * 8м/с * 2с = 8м
Итого S = 1м + 2м + 8м = 11м

3. А если скорость равна нулю?

Не стоит пугаться нулевых скоростей на каком-либо интервале времени. Например с 3с по 5с на графике, представленном на рис. 3 перемещение тела равно 0м, т. к. площадь фигуры с 3с по 5с равна 0.

4. А если скорость ушла “в минус”?

А вот отрицательная скорость может вызвать некоторые затруднения. Здесь надо очень внимательно читать задание и не перепутать очень похожие физические величины: путь и перемещение. Путь – величина скалярная и поэтому для ее нахождения с помощью графика на рис. 4 надо зеркально отобразить отрицательные участки скорости и сложить площади фигур (см. Рис. 5)

Перемещение – величина векторная и поэтому при определении этой величины необходимо учитывать знак площади. Например, если нужно найти перемещение тела с 0с по 10с (см. рис. 5), то нужно площадь треугольника с 0с по 4с сложить с площадью треугольника с 8с по 10с и из полученного результата вычесть площадь треугольника с 4с по 8с.

5. Когда можно и не считать!

Иногда требуется визуальный анализ графиков. Например, необходимо определить какой автомобиль из 4-х с 0с до 15с проехал наибольшее расстояние?
Рассматривая площади геометрических фигур под графиками (см. рис. 6) видим, что площадь больше у графика (и машины) №3.

6. Переходим к ускорению

До сих пор мы на линейных графиках с координатами скорости и времени (см. рис. 7) видели скорость, время и перемещение (или путь).

А тут ещё прячется ускорение. Давайте попробуем его найти. Вспоминаем формулу равноускоренного движения

Рассматривая график на рис. 7 определим Vo при t = 0с => Vo = 2м/с.
А теперь возьмём на графике точку в момент времени t = 1c и определим по графику скорость в этот момент времени => V = 4м/с.
Подставляем найденные значения в формулу 2 =>
4м/с = 2м/с + a * 1c => а = (4м/с – 2м/с) / 1с = 2м/с2

Возвращаемся к графику (см. рис. 8)

Теперь мы можем сказать, что на рис. 8 представлен график линейного уравнения V = Vo + a*t = 2 + 2*t. Эти знания расширяют область использования графика на рис. 8. Например мы можем сказать, что при
t = 10c скорость будет равна V = 2м/с + 2м/с2*10с = 22м/с

7. Ищем ускорение на произвольном прямолинейном участке графика

Нас могут попросить найти ускорение тела на произвольном прямолинейном участке графика. Например с 6с по 10с на графике, представленном на рис. 9.

Для этого получим формулу для ускорения, усложнив формулу 2 заменив t на (t – to):

Возвращаемся к поиску ускорения:
а = (5м/с – (-5м/с))/(10с – 6с) = 10м/с / 4с = 2.5м/с2

8. Ищем координаты тела

Зная начальные координаты тела, начальную скорость, ускорение тела и время перемещения можем найти координаты тела в любой момент времен (формула 4)

9. Ищем скорость в пространстве

Мы можем знать значение проекций скорости на оси: х, y и z. Нас могут попросить найти модуль скорости. Ищем по формуле 5:

Для понимания формулы 5 можно представить модуль скорости диагональю параллелепипеда, а проекции скорости сторонами параллелепипеда (см. рис. 11)

Заключение

Пока, это все мысли, которые появлялись во время решения задач в разделе сайта “Решу ЕГЭ” по адресу https://phys-ege.sdamgia.ru/test?theme=204. Пишите в комментариях, если что-то напрашивается добавить.

Автор с благодарностью примет любые пожертвования на развитие канала “От сложного к простому” https://money.yandex.ru/to/4100170126360.