Как найти скорость планеты вокруг солнца

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 июля 2021 года; проверки требуют 10 правок.

Файл:Скорость небесного тела

Скорость кеплеровского движения небесного тела вокруг Солнца, а также её радиальная и поперечная компоненты (анимация).

Орбитальная скорость тела (обычно планеты, естественного или искусственного спутника, кратной звезды) — скорость, с которой оно вращается вокруг барицентра системы, как правило вокруг более массивного тела.

Определение[править | править код]

В полярных координатах выражение для орбитальной скорости при кеплеровском движении по коническому сечению (эллипсу, параболе или гиперболе) имеет следующий вид^[1]:

${displaystyle v={sqrt {{frac {mu }{p}}(1+2varepsilon cos theta +varepsilon ^{2})}},}$

где:

— гравитационный параметр, равный G(M + m) — в общей задаче двух тел, или GM — в ограниченной, где G — гравитационная постоянная, M — масса центрального тела, m — масса вращающегося тела;

— фокальный параметр конического сечения (расстояние от фокуса до директрисы для параболы, отношение ${displaystyle b^{2}/a}$

— для эллипса и гиперболы);

— эксцентриситет (

для эллипса,

для параболы,

— для гиперболы);

— истинная аномалия, угол между направлением из центра, расположенного в фокусе, на ближайшую к нему точку орбиты и радиусом-вектором вращающегося тела.

Орбитальная скорость также может вычисляться по общей формуле

${displaystyle v={sqrt {2left({frac {mu }{r}}+epsilon right)}}={sqrt {mu left({frac {2}{r}}-{frac {1}{a}}right)}},}$

где

— гравитационный параметр,

— расстояние между вращающимся телом и центральным телом,

— удельная орбитальная энергия,

— длина большой полуоси (или вещественной оси).

При этом

Орбиты Земли[править | править код]

Орбита	Расстояние между центрами масс, км	Высота над поверхностью Земли, км	Орбитальная скорость, км/с	Орбитальный период	Удельная орбитальная энергия, МДж/кг
Поверхность Земли, для сравнения	6 400	0	7,89	—	−62,6
Низкая околоземная орбита	6 600—8 400	200—2 000	круговая: 7,8—6,9 эллиптическая: 6,5—8,2	89—128 мин	−29,8
Высокоэллиптическая орбита спутников Молния	6 900—46 300	500—39 900	1,5—10,0	11 ч 58 мин	−4,7
Геостационарная орбита	42 000	35 786	3,1	23 ч 56 мин	−4,6
Орбита Луны	363 000—406 000	357 000—399 000	0,97—1,08	27,3 дня	−0,5

Солнечная система[править | править код]

Планета (другое тело)	Орбитальная скорость, км/с
Меркурий	47,36
Венера	35,02
Земля	29,78
Марс	24,13
Церера	17,88
Юпитер	13,07
Сатурн	9,69
Уран	6,81
Нептун	5,43
Плутон	4,66
Хаумеа	4,48
Макемаке	4,41
Эрида	3,43
Луна	1,02

Примечания[править | править код]

↑ Балк М. Б. Скорость спутника и её компоненты // Элементы динамики космического полета. — М.: Наука, 1965. — С. 61—62. — 340 с. — (Механика космического полета).

Источник

Мы уже рассчитывали линейную и угловую скорости вращения Земли вокруг своей собственной оси. Давайте сегодня рассмотрим движение Земли вокруг Солнца, и найдем скорость этого движения. Ну, и заодно, рассмотрим три закона Кеплера. Куда без них.

Первый способ

С какой скоростью вращается Земля вокруг Солнца? Первое что приходит в голову, это воспользоваться уже знакомым уравнением для нахождения линейной скорости:

$[upsilon =frac {2pi R}{T}]$

Расстояние от Земли до Солнца одна астрономическая единица или 149 597 870 700 м. Период обращения составляет один год. Если перевести это в секунды мы получим 31 536 000 с.

Подставляем это все в наше уравнение и считаем.

$upsilon =frac {2*3,14 *149 597 870 700}{31536000} approx 29 790,545$ м/с

Второй способ

Но можно и пойти другим путем. Скорость движения Земли будет являться первой космической скоростью в поле тяготения Солнца. По этому, вспоминаем уравнение для нахождения первой космической скорости.

$[v =sqrt{frac {G*M_c}{R}}]$

Где G -это гравитационная постоянная, R — расстояние от Земли до Солнца, ну и M — масса самого Солнца. Остается только взвесить Солнце и произвести расчет:

$v =sqrt{frac {G*M_c}{R}} = sqrt{frac {6.67cdot 10^{-11}cdot 1.9985 cdot 10^{30}}{1.496cdot 10^{11}}}approx 29775.559$ м/с

Часто для удобства скорость округляют и представляют как 30 км/с или 108 000 км/ч. Последний вариант, кстати, очень любят индусы. Так как в индуизме число 108 считается священным. Они даже число Пи, в свое время, определяли как отношение 339/108. Но вернемся к скорости.

Первый закон Кеплера

В наших расчетах мы принимали что Земля равномерно движется по окружности. Хотя в реальности это не совсем так.

Иоганн Кеплер (1571 — 1630 гг).

Еще в начале XVII века немецкий астроном Иоганн Кеплер, опираясь на данные многолетних наблюдений за планетой Марс, полученные его учителем — датским астрономом Тихо Браге, заключил, что все планеты солнечной системы движутся не по окружности, а по эллипсу, в одном из фокусов которого находится Солнце. Этот закон называют первым законом Кеплера.

Все планеты Солнечной Системы движутся по эллипсу, в одном из фокусов которого находится Солнце.

Так что давайте разобраться что такое такое эллипс, и в чем его фокус.. или фокусы.

Что такое эллипс?

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

Рассмотрим все на простом примере. Берем шнурок с канцелярскими кнопками-гвоздиками на концах. Втыкаем кнопки в кусок гипсокартонна, который завалялся в гараже после ремонта.

Далее карандашом, опираясь на шнурок рисуем линии. Получившаяся фигура и есть эллипс, а точки куда мы втыкали кнопки называются фокусами.

Большая и малая полуось

Важными характеристиками эллипса являются его полуоси. Большая ее обычно обозначают латинской буквой «a», и малая, которую обозначают буквой «b». Тоже латинской.

Большая полуось — это расстояния от центра эллипса до самой дальней его точки. Соответственно, малая полуось — это расстояние от центра до самой ближней точки эллипса.

Эксцентриситет

Еще одна важная характеристика эллипса носит шикарное название — эксцентриситет. Его обычно обозначают буквой «е» и определяют как отношение фокусного расстояния эллипса (c) к большой полуоси (a).

$[e =frac {c}{a}]$

Эллипс иногда называют сплющенной окружностью. Так вот эксцентриситет как раз показывает насколько эта окружность сплющена.

Для эллипса:

Чем ближе эксцентриситет к единице, тем более вытянутый эллипс мы получим. И наоборот эксцентриситет близкий к 0, будет иметь эллипс ну очень похожий на окружность. В принципе можно сказать что окружность это эллипс с е=0.

В солнечной системе самый маленький эксцентриситет у Венеры всего 0,007, то есть траектория ее движения это практически окружность. Эксцентриситет близкий к единице имеют кометы. К примеру у кометы Галея е=0,967.

Что же касается Земли, то эксцентриситет земной орбиты тоже очень близок к нулю, всего 0,017. Но тем не менее это не ноль. А это значит что расстояние от Земли до Солнца величина отнюдь не постоянная.

Афелий и перигелий

Точка в которой планета находится ближе всего к Солнцу называется перигелий. От греческого perihelion, “peri“ — рядом и “helios“ — Солнце. Противоположная перигелию точка называется афелий. Соответственно это точка где планета максимально удалена от светила.

Земля находится перигелии, начале января. Она приближается к Солнцу на расстояние в 147,1 миллионов километров. Афелий она проходит в начале июля, когда удаляется на 152,1 миллионов километров. Разница выходит около 5 миллионов километров.

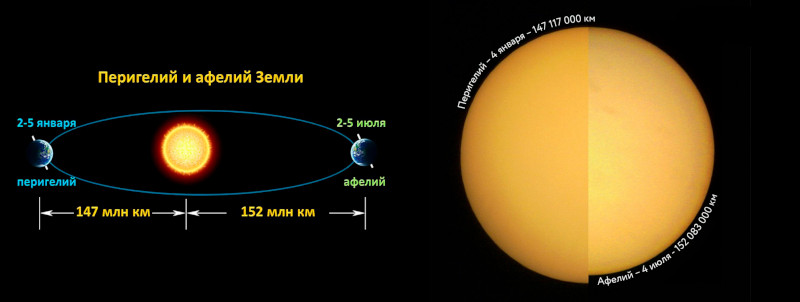
Этим иногда объясняют то что зимы в северном полушарии менее суровые, нежели в южном. Все таки зимой мы чуть ближе к солнцу. С другой стороны так как земля получает меньше солнечной энергии в июле, лето в северном полушарии более прохладное.

Второй закон Кеплера

Итак, мы сказали что согласно первому закону Кеплера Земля движется не по круговой, а по эллиптической орбите. Что же касается ее скорости, то она возрастает при приближении к Солнцу, и убывает при удалении от него.

Кеплер сформулировал это следующим образом:

За одинаковые промежутки времени радиус-вектор планеты описывает одинаковые площади.

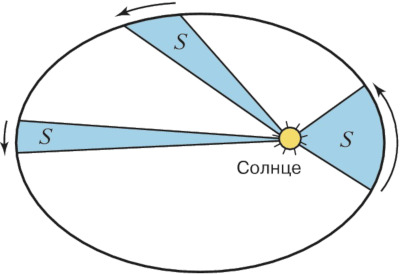
Это так называемый закон площадей или второй закон Кеплера, пожалуй в самой бесполезной его формулировке. Но фактически мы имеем дело с законом сохранения момента импульса. И куда больший интерес для нас будет иметь следующее уравнение:

Произведение линейной скорости и радиус-вектора в перигелии, равно произведению скорости и радиус-вектора афелии. Это частный случай второго закона Кеплера, соответственно для максимального и минимального значений скорости движения планеты.

Максимальная и минимальная скорость движения Земли

Зная это можно, рассчитать с какими скоростями движется Земля перигелии и афелии. То есть найти ее максимальную и минимальную скорости. Но здесь нам понадобится закон сохранения энергии.

$[frac {mupsilon_1^2}{2} - G frac { M_c cdot m}{r_1} = frac {mupsilon_2^2}{2} - G frac {M_c cdot m}{r_2}]$

А так же, формулы для определения расстояний от солнца до афелия и перигелия, через эксцентриситет и большую полуось:

Ну и пожалуй уравнение для нахождения первой космической скорости.

$[upsilon =sqrt{frac {G*M_c}{R}}]$

Единственное в формуле расстояние R мы заменим на a, то есть на большую полуось. Большая полуось земной орбиты — это среднее расстояние от Земли до Солнца, и именно значение большой полуоси мы использовали в расчетах в самом начале. А значит скорость которую мы рассчитывали в самом начале есть средняя орбитальная. Она нам пригодится.

$[upsilon =sqrt{frac {G*M_c}{a}}]$

Составляем небольшую систему уравнения и с точки зрения физики задача решена. Остается только математика.

$[begin{cases} upsilon_1cdot r_1 =upsilon_2cdot r_2\ frac {mupsilon_1^2}{2} - G frac { M_c cdot m}{r_1} = frac {mupsilon_2^2}{2} - G frac {M_c cdot m}{r_2}\ r_1 = a(1-e)\ r_2 = a(1+e)\ upsilon =sqrt{frac {G*M_c}{a}} end{cases}]$

Начнем с того, что сократим массу Земли в законе сохранения энергии, а так же заменим радиус векторы на, соответственно, , .

$[begin{cases} upsilon_1cdot a(1-e) =upsilon_2cdot a(1+e)\ frac {upsilon_1^2}{2} - G frac { M_c}{a(1-e)} = frac {upsilon_2^2}{2} - G frac {M_c}{a(1+e)}\ upsilon =sqrt{frac {G*M_c}{a}} end{cases}]$

Если внимательно посмотреть, то можно увидеть что в отношениях $G frac { M_c}{a(1-e)}$ , и $G frac {M_c}{a(1+e)}$ , $G frac {M_c}{a}$ , это квадрат средней орбитальной скорости . А ее мы уже рассчитали в самом начале. Так что здесь удобно будет выполнить замену.

$[begin{cases} upsilon_1cdot a(1-e) =upsilon_2cdot a(1+e)\ frac {upsilon_1^2}{2} - frac { upsilon ^2}{1-e} = frac {upsilon_2^2}{2} - G frac {upsilon ^2}{1+e}]$

Теперь из первого уравнения выражаем , и подставляем это все во второе. Делаем все необходимые преобразования и выражаем :

$[upsilon_1 =upsilon sqrt{frac {1+e}{1-e}}]$

Ну и теперь так же выражаем :

$[upsilon_2 =upsilon sqrt{frac {1-e}{1+e}}]$

Остается только подставить значения, и посчитать.

$upsilon_1 = 29775.559 sqrt{frac {1+0.017}{1-0.017}} approx 30 286,1$ м/с

$upsilon_2 = 29775.559 sqrt{frac {1-0.017}{1+0.017}} approx 29 273,6$ м/с

Третий закон Кеплера

Опубликовав в 1609 г. два своих закона Иоганн Кеплер так и не остался удовлетворен, и продолжил поиски, которые спустя десять лет привели его к открытию третьего закона.

Квадраты звездных периодов обращений планет относятся между собой как кубы больших полуосей их орбит.

$[frac {T_1^2}{T_2^2}} =frac {a_1^3}{a_2^3}}]$

Но это уже совсем другая история…

Источник

From Wikipedia, the free encyclopedia

In gravitationally bound systems, the orbital speed of an astronomical body or object (e.g. planet, moon, artificial satellite, spacecraft, or star) is the speed at which it orbits around either the barycenter or, if one body is much more massive than the other bodies of the system combined, its speed relative to the center of mass of the most massive body.

The term can be used to refer to either the mean orbital speed (i.e. the average speed over an entire orbit) or its instantaneous speed at a particular point in its orbit. The maximum (instantaneous) orbital speed occurs at periapsis (perigee, perihelion, etc.), while the minimum speed for objects in closed orbits occurs at apoapsis (apogee, aphelion, etc.). In ideal two-body systems, objects in open orbits continue to slow down forever as their distance to the barycenter increases.

When a system approximates a two-body system, instantaneous orbital speed at a given point of the orbit can be computed from its distance to the central body and the object’s specific orbital energy, sometimes called “total energy”. Specific orbital energy is constant and independent of position.^[1]

Radial trajectories[edit]

In the following, it is thought that the system is a two-body system and the orbiting object has a negligible mass compared to the larger (central) object. In real-world orbital mechanics, it is the system’s barycenter, not the larger object, which is at the focus.

Specific orbital energy, or total energy, is equal to E_k − E_p. (kinetic energy − potential energy). The sign of the result may be positive, zero, or negative and the sign tells us something about the type of orbit:^[1]

If the specific orbital energy is positive the orbit is unbound, or open, and will follow a hyperbola with the larger body the focus of the hyperbola. Objects in open orbits do not return; once past periapsis their distance from the focus increases without bound. See radial hyperbolic trajectory
If the total energy is zero, (E_k = E_p): the orbit is a parabola with focus at the other body. See radial parabolic trajectory. Parabolic orbits are also open.
If the total energy is negative, E_k − E_p < 0: The orbit is bound, or closed. The motion will be on an ellipse with one focus at the other body. See radial elliptic trajectory, free-fall time. Planets have bound orbits around the Sun.

Transverse orbital speed[edit]

The transverse orbital speed is inversely proportional to the distance to the central body because of the law of conservation of angular momentum, or equivalently, Kepler’s second law. This states that as a body moves around its orbit during a fixed amount of time, the line from the barycenter to the body sweeps a constant area of the orbital plane, regardless of which part of its orbit the body traces during that period of time.^[2]

This law implies that the body moves slower near its apoapsis than near its periapsis, because at the smaller distance along the arc it needs to move faster to cover the same area.^[1]

Mean orbital speed[edit]

For orbits with small eccentricity, the length of the orbit
is close to that of a circular one, and the mean orbital speed can be approximated either from observations of the orbital period and the semimajor axis of its orbit, or from knowledge of the masses of the two bodies and the semimajor axis.^[3]

{displaystyle vapprox {2pi a over T}approx {sqrt {mu over a}}}

where v is the orbital velocity, a is the length of the semimajor axis, T is the orbital period, and μ = GM is the standard gravitational parameter. This is an approximation that only holds true when the orbiting body is of considerably lesser mass than the central one, and eccentricity is close to zero.

When one of the bodies is not of considerably lesser mass see: Gravitational two-body problem

So, when one of the masses is almost negligible compared to the other mass, as the case for Earth and Sun, one can approximate the orbit velocity v_o as:^[1]

$v_{o}approx {sqrt {{frac {GM}{r}}}}$

or assuming r equal to the radius of the orbit^{[citation needed]}

$v_{o}approx {frac {v_{e}}{{sqrt {2}}}}$

Where M is the (greater) mass around which this negligible mass or body is orbiting, and v_e is the escape velocity.

For an object in an eccentric orbit orbiting a much larger body, the length of the orbit decreases with orbital eccentricity e, and is an ellipse. This can be used to obtain a more accurate estimate of the average orbital speed:^[4]

${displaystyle v_{o}={frac {2pi a}{T}}left[1-{frac {1}{4}}e^{2}-{frac {3}{64}}e^{4}-{frac {5}{256}}e^{6}-{frac {175}{16384}}e^{8}-cdots right]}$

The mean orbital speed decreases with eccentricity.

Instantaneous orbital speed[edit]

For the instantaneous orbital speed of a body at any given point in its trajectory, both the mean distance and the instantaneous distance are taken into account:

v={sqrt {mu left({2 over r}-{1 over a}right)}}

where μ is the standard gravitational parameter of the orbited body, r is the distance at which the speed is to be calculated, and a is the length of the semi-major axis of the elliptical orbit. This expression is called the vis-viva equation.^[1]

For the Earth at perihelion, the value is:

${displaystyle {sqrt {1.327times 10^{20}~{text{m}}^{3}{text{s}}^{-2}cdot left({2 over 1.471times 10^{11}~{text{m}}}-{1 over 1.496times 10^{11}~{text{m}}}right)}}approx 30,300~{text{m}}/{text{s}}}$

which is slightly faster than Earth’s average orbital speed of 29,800 m/s (67,000 mph), as expected from Kepler’s 2nd Law.

Tangential velocities at altitude[edit]

Orbit	Center-to-center distance	Altitude above the Earth’s surface	Speed	Orbital period	Specific orbital energy
Earth’s own rotation at surface (for comparison— not an orbit)	6,378 km	0 km	465.1 m/s (1,674 km/h or 1,040 mph)	23 h 56 min 4.09 sec	−62.6 MJ/kg
Orbiting at Earth’s surface (equator) theoretical	6,378 km	0 km	7.9 km/s (28,440 km/h or 17,672 mph)	1 h 24 min 18 sec	−31.2 MJ/kg
Low Earth orbit	6,600–8,400 km	200–2,000 km	Circular orbit: 6.9–7.8 km/s (24,840–28,080 km/h or 14,430–17,450 mph) respectively Elliptic orbit: 6.5–8.2 km/s respectively	1 h 29 min – 2 h 8 min	−29.8 MJ/kg
Molniya orbit	6,900–46,300 km	500–39,900 km	1.5–10.0 km/s (5,400–36,000 km/h or 3,335–22,370 mph) respectively	11 h 58 min	−4.7 MJ/kg
Geostationary	42,000 km	35,786 km	3.1 km/s (11,600 km/h or 6,935 mph)	23 h 56 min 4.09 sec	−4.6 MJ/kg
Orbit of the Moon	363,000–406,000 km	357,000–399,000 km	0.97–1.08 km/s (3,492–3,888 km/h or 2,170–2,416 mph) respectively	27.27 days	−0.5 MJ/kg

The lower axis gives orbital speeds of some orbits

Planets[edit]

The closer an object is to the Sun the faster it needs to move to maintain the orbit. Objects move fastest at perihelion (closest approach to the Sun) and slowest at aphelion (furthest distance from the Sun). Since planets in the Solar System are in nearly circular orbits their individual orbital velocities do not vary much. Being closest to the Sun and having the most eccentric orbit, Mercury’s orbital speed varies from about 59 km/s at perihelion to 39 km/s at aphelion.^[5]

Orbital velocities of the Planets^[6]

Planet	Orbital velocity
Mercury	47.9 km/s (29.8 mi/s)
Venus	35.0 km/s (21.7 mi/s)
Earth	29.8 km/s (18.5 mi/s)
Mars	24.1 km/s (15.0 mi/s)
Jupiter	13.1 km/s (8.1 mi/s)
Saturn	9.7 km/s (6.0 mi/s)
Uranus	6.8 km/s (4.2 mi/s)
Neptune	5.4 km/s (3.4 mi/s)

Halley’s Comet on an eccentric orbit that reaches beyond Neptune will be moving 54.6 km/s when 0.586 AU (87,700 thousand km) from the Sun, 41.5 km/s when 1 AU from the Sun (passing Earth’s orbit), and roughly 1 km/s at aphelion 35 AU (5.2 billion km) from the Sun.^[7] Objects passing Earth’s orbit going faster than 42.1 km/s have achieved escape velocity and will be ejected from the Solar System if not slowed down by a gravitational interaction with a planet.

Velocities of better-known numbered objects that have perihelion close to the Sun

Object	Velocity at perihelion	Velocity at 1 AU (passing Earth’s orbit)
322P/SOHO	181 km/s @ 0.0537 AU	37.7 km/s
96P/Machholz	118 km/s @ 0.124 AU	38.5 km/s
3200 Phaethon	109 km/s @ 0.140 AU	32.7 km/s
1566 Icarus	93.1 km/s @ 0.187 AU	30.9 km/s
66391 Moshup	86.5 km/s @ 0.200 AU	19.8 km/s
1P/Halley	54.6 km/s @ 0.586 AU	41.5 km/s

References[edit]

^ ^a ^b ^c ^d ^e Lissauer, Jack J.; de Pater, Imke (2019). Fundamental Planetary Sciences: physics, chemistry, and habitability. New York, NY, USA: Cambridge University Press. pp. 29–31. ISBN 9781108411981.
^ Gamow, George (1962). Gravity. New York, NY, USA: Anchor Books, Doubleday & Co. pp. 66. ISBN 0-486-42563-0. …the motion of planets along their elliptical orbits proceeds in such a way that an imaginary line connecting the Sun with the planet sweeps over equal areas of the planetary orbit in equal intervals of time.
^ Wertz, James R.; Larson, Wiley J., eds. (2010). Space mission analysis and design (3rd ed.). Hawthorne, CA, USA: Microcosm. p. 135. ISBN 978-1881883-10-4.
^ Stöcker, Horst; Harris, John W. (1998). Handbook of Mathematics and Computational Science. Springer. pp. 386. ISBN 0-387-94746-9.
^ “Horizons Batch for Mercury aphelion (2021-Jun-10) to perihelion (2021-Jul-24)”. JPL Horizons (VmagSn is velocity with respect to Sun.). Jet Propulsion Laboratory. Retrieved 26 August 2021.
^ “Which Planet Orbits our Sun the Fastest?”.
^ v = 42.1219 √1/r − 0.5/a, where r is the distance from the Sun, and a is the major semi-axis.

Источник

Как можно вычислить скорость движения Земли вокруг Солнца?

Александра Шилова

Ученик

(82),
закрыт

9 лет назад

Дополнен 9 лет назад

Вот есть формула: скорость движения тела = путь пройденный телом разделить на время движения тела.

Дополнен 9 лет назад

Еще есть несколько формул…. Или l или t =2п=пd….и l=150000000 км. ну путь пройденый телом это понятно…. что такое п и пd?

Трудное детство

Оракул

(70151)

9 лет назад

среднюю скорость из равенства сил, тяготения и центробежной. mV^2/R=GMm/R^2. отсюда V=(GM/R)^1/2, где M масса солнца, а R – средний радиус земной орбиты. для нахождения мгновенной скорости надо использовать 2 закон кеплера.

daybit

Высший разум

(146345)

9 лет назад

Длина орбиты Земли равна 2*pi*R, где pi = 3.14, а радиус орбиты R = 150 млн км. Итого длина орбиты = 942 000 000 км.

В году 365.25 дней, в сутках 24 часа, в 1 часе 3600 секунд, все перемножаем и получаем 365,25*24*3600 = 31 557 600 сек.

Делим 942 000 000 км на 31 557 600 сек, получаем 29.85 км/сек

Источник

Физика, космос, планеты, астрономия, космонавтика · 23 мая 2021

Для этого нужно вспомнить формулу линейной скорости при круговом вращении

V = (2*П*R)/T,

где R – радиус, он же расстояние от Земли до Солнца (150 млн. км),

Т – период обращения Земли (1 год).

Затем нужно перевести километры в метры, года в секунды и подставить численные значения. При правильных расчетах должно получиться 30000 м/сек, т.е. 30 км/сек.

2,5 K

средняя скорость движения Земли по орбите вокруг Солнца составляет

29,78 км/с

Комментировать ответ…Комментировать…

Ответы на похожие вопросы

С какой скоростью вращается земля по солнечной орбите? — 2 ответа, задан 23 мая 2021

Космология, физика, военная техника, авиация и ракетостроение. Шахматы слегка, поделки и… · 8 июл 2021

Земля ВРАЩАЕТСЯ вокруг своей оси со скоростью один оборот в сутки, а ОБРАЩАЕТСЯ вокруг Солнца за один год. При этом поступательная скорость движения Земли по орбите вокруг Солнца составляет около 30 кмсек. В свою очередь Солнце, находясь в одном из трех рукавов Галактики, обращается вокруг ее центра с известной скоростью, увлекая за собой все планеты и другие объекты Солнечной системы, тем самым придавая им соответствующую дополнительную скорость поступательного движения (но это вне рамок заданного вопроса)…

425

Комментировать ответ…Комментировать…

Источник

Определение[править | править код]

Орбиты Земли[править | править код]

Солнечная система[править | править код]