Как найти собственную скорость лодки
Решение задач на «движение по воде» многим дается с трудом. В них существует несколько видов скоростей, поэтому решающие начинаю путаться. Чтобы научиться решать задачи такого типа, надо знать определения и формулы. Умение составлять схемы очень облегчает понимание задачи, способствует правильному составлению уравнения. А правильно составленное уравнение – самое главное в решении любого типа задач.

Инструкция
В задачах «на движение по реке» присутствуют скорости: собственная скорость (Vс), скорость по течению (Vпо теч.), скорость против течения (Vпр. теч.), скорость течения (Vтеч.). Необходимо отметить, что собственная скорость водного суда – это скорость в стоячей воде. Чтобы найти скорость по течению, надо к скорости течения прибавить собственную. Для того чтобы найти скорость против течения, надо из собственной скорости вычесть скорость течения.
Первое, что необходимо выучить и знать “на зубок” – формулы. Запишите и запомните:
Vпо теч=Vс+Vтеч.
Vпр. теч.=Vс-Vтеч.
Vпр. теч=Vпо теч. – 2Vтеч.
Vпо теч.=Vпр. теч+2Vтеч.
Vтеч.=(Vпо теч. – Vпр. теч)/2
Vс=(Vпо теч.+Vпр теч.)/2 или Vс=Vпо теч.+Vтеч.
На примере разберем, как находить собственную скорость и решать задачи такого типа.
Пример 1.Скорость лодки по течению 21,8км/ч, а против течения 17,2 км/ч. Найти собственную скорость лодки и скорость течения реки.
Решение: Согласно формулам: Vс=(Vпо теч.+Vпр теч.)/2 и Vтеч.=(Vпо теч. – Vпр. теч)/2, найдем:
Vтеч = (21,8 – 17,2)/2=4,62=2,3 (км/ч)
Vс = Vпр теч.+Vтеч=17,2+2,3=19,5 (км/ч)
Ответ: Vc=19,5 (км/ч), Vтеч=2,3 (км/ч).
Пример 2. Пароход прошел против течения 24 км и вернулся обратно, затратив на обратный путь на 20 мин меньше, чем при движении против течения. Найдите его собственную скорость в неподвижной воде, если скорость течения равна 3 км/ч.
За Х примем собственную скорость парохода. Составим таблицу, куда занесем все данные.
Против теч. По течению
Расстояние 24 24
Скорость Х-3 Х+3
время 24/ (Х-3) 24/ (Х+3)
Зная, что на обратный путь пароход затратил на 20 минут времени меньше, чем на путь по течению, составим и решим уравнение.
20 мин=1/3 часа.
24/ (Х-3) – 24/ (Х+3) = 1/3
24*3(Х+3) – (24*3(Х-3)) – ((Х-3)(Х+3))=0
72Х+216-72Х+216-Х2+9=0
441-Х2=0
Х2=441
Х=21(км/ч) – собственная скорость парохода.
Ответ: 21 км/ч.
Обратите внимание
Скорость плота считается равной скорости водоема.
Источники:
- решение задач на течение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Здравствуйте, дорогие читатели, подписчики и гости канала. Продолжаем разбор текстовых задач из ОГЭ 2021 года, входящие в 21 задание. Рассмотрим решение задач на движение по воде. В задачах за неизвестное (Х) будем брать то, что нужно найти.
Задача №1
Пусть Х – собственная скорость баржи. Если баржа плывет по течению реки, то ее собственная скорость увеличивается на скорость реки, и наоборот. Все данные из задачи перенесем в таблицу.
Так как весь путь по течению реки и против течения составил 5 часов, то составим уравнение:
Решим уравнение:
Задача №2
Пусть Х – скорость лодки в неподвижной воде. Тогда по течению реки будет Х+5, против течения реки Х-5.
Важно! Скорость течения реки равна 3 км/ч, с этой же скорость плывет плот, так как у плота нет своей скорости. Зная скорость плота и расстояние, которое плыл плот. Время, которое плыл плот равно: 33:3=11 часов.
Моторная лодка вышла вслед за плотом через один час, значит она плыла 10 часов. Составим уравнение:
Решим уравнение:
Задача №3
Пусть Х – скорость лодки в неподвижной воде. Тогда скорость лодки по течению будет равна Х+4, против течения Х-4. Внесем все данные в таблицу и найдем время движения лодки по течению и против течения реки.
Время движения против течения реки больше чем время движения по течению на 2 часа. Составим уравнение:
Решим уравнение, найдем скорость лодки в неподвижной воде:
Задача №4
Пусть Х – скорость течения реки. Тогда скорость теплохода по течению реки будет 25+х, против течения – 25-х.
Найдем, сколько времени был теплоход в пути. Теплоход вернулся в пункт отправления через 32 часа, а стоял в пункте назначения 21 час, значит в пути по воде в обе стороны теплоход плыл 32-21=11 часов.
Составим уравнение:
Решим уравнение и найдем скорость течения реки:
Спасибо, что дочитали. Вы меня очень поддержите, если поставите класс и подпишитесь на мой блог.
Путеводитель по каналу здесь
§ 1 Методика решения задач на движение по течению и против течения
Из всех текстовых задач на движение особое место занимают задачи на движение по течению и против течения реки. Для успешного их решения необходимо различать 4 вида движения: течение реки, собственное движение, движение по течению и движение против течения реки.
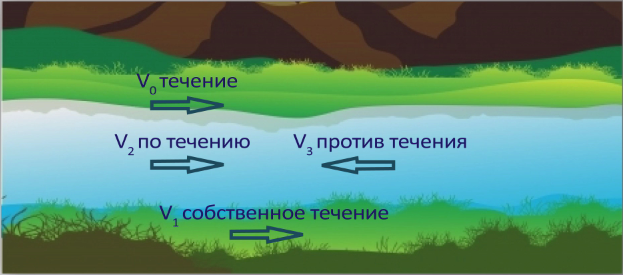
Вид движения «течение реки» встречается в тех задачах, в которых рассматриваются движения немеханизированных объектов, например, движение плота. Такой вид движения возможен только по течению и скорость движущегося объекта всегда совпадает со скоростью течения реки.
Собственное движение характерно для механизированных объектов в стоячей воде, например, катер движется по озеру.
Движение по течению и движение против течения реки формируется из двух видов движения – собственного и течения реки.
При движении по течению направления течения реки и движения объекта совпадают, поэтому скорость перемещения тела при этом виде движения равна сумме собственной скорости тела и скорости течения
vсобств + vтечения.
При движении против течения течение реки препятствует движению объекта, поэтому скорость перемещения тела при этом виде движения равна разности собственной скорости тела и скорости течения
vсобств– vтечения.
Полезно знать, что сумма скоростей по течению и против течения реки равна удвоенной собственной скорости
vпо теч + vпротив теч = 2vсобств,
а разность этих скоростей равна удвоенной скорости течения реки
vпо теч – vпротив теч = 2vтечения.
Часто упрощает решение задач на движение понимание взаимной обратной зависимости скорости и времени движения: чем больше время, тем меньше скорость движения, и, наоборот, чем больше скорость движения, тем меньше времени тратится на прохождение пути.
В качестве неизвестных в таких текстовых задачах удобно выбирать расстояние и скорости движущихся тел, если они не заданы. В задачах, где в условии не представлены единицы длины, принято весь путь брать за единицу длины, а часть этого пути выражают долей всего пути без наименования.
В текстовых задачах на движение, связанных с течением реки, при проведении смысловой проверки полезно знать, что моторная лодка имеет собственную скорость12 – 40 км/ч, скорость течения реки изменяется в пределах 1 – 4км/ч, а скорость лодки на вёслах составляет примерно 3 – 8км/ч.
Рассмотрим приёмы решения текстовых задач на движение по течению и против течения на примерах решения следующих задач.
§ 2 Примеры решения задач на движение по течению и против течения
Задача 1.От пристани А до пристани В моторная лодка по течению реки проходит за 6 часов, а возвращается за 10 часов. За сколько часов пройдёт расстояние от А до В плот?
РЕШЕНИЕ.Решим задачу арифметическим способом.

Мы знаем, что расстояние определяется по формуле S = vt, где v– скорость лодки, t– время движения лодки, выраженное в часах. В задаче не используются единицы длины, значит, расстояние от А до В обозначим за единицу 1.
По условию задачи моторная лодка по течению реки проходит за 6 часов, значит, скорость по течению реки равна 1 : 6.
Моторная лодка возвращается за 10 часов, значит, расстояние АВ против течения реки лодка проходит за 10 часов, следовательно, её скорость при таком движении равна одной десятой. Для того, чтобы найти время движения плота на дистанции АВ, надо найти скорость плота, которая совпадает со скоростью течения реки. Известно, что удвоенная скорость течения реки равна разности скоростей по течению и против течения, то есть
2vтечения = vпо теч – vпротив теч.
Вычислив разность скоростей по течению и против течения реки, имеем ![]()
Таким образом, решив уравнение
![]()
получаем, что скорость течения реки

Получили, что за 1 час плот проплывёт одну тридцатую всего пути от пункта А до пункта В.
Чтобы найти время движения плота, надо путь 1 единицу разделить на скорость его движения.
Получили, что плот пройдёт расстояние от А до В за 30часов.
Ответ: 30 часов.
А теперь рассмотрим алгебраический способ решения данной задачи. введём переменные пусть х км/ч – собственная скорость моторной лодки, у км/ч – скорость течения реки.
Cоставим таблицу данных с введёнными переменными.

Обозначим в столбцах таблицы элементы движения:
v– скорость, выраженная в км/ч,
t– время, выраженное в часах,
S– расстояние, выраженное в км.
В строках – виды движения: собственное движение, течение, движение по течению, движение против течения. Заметим, что движение течения и движение плота – это идентичные виды движения. Заполним таблицу согласно условий задачи.
В собственном виде движения мы ввели скорость движения лодки х км/ч, внесём её в соответствующую ячейку таблицы, в ячейках t и S поставим прочерк, так как эти данные не используются в данной задаче. В движении плота мы ввели скорость течения реки у км/ч, внесём в таблицу, а ячейки t и S заполним позже.
В движении по течению реки выразим скорость v суммой скоростей лодки и течения, то есть х + у км/ч, время t по условию задачи равно 6ч, значит, можем выразить расстояние от пункта А до пункта В. Оно равно 6(х + у)км.
В движении против течения реки выразим скорость vразностью скоростей лодки и течения, то есть х – у км/ч, время t по условию задачи равно 10ч, значит, можем выразить расстояние от пункта А до пункта В. Оно равно 10(х – у)км.
В движениях по течению и против течения реки расстояния равны между собой, значит, можем составить уравнение 6(х + у) = 10(х – у).
Дополним строку движения плота: расстояние S будет равно расстоянию движения по течению или против течения, значит, можем вписать выражение 6(х + у) км или 10(х – у) км.
Теперь можем выразить время движения плота
![]()
Или
![]()
Из уравнения 6(х + у) = 10(х – у) выразим одну переменную через другую, например, переменную х через у.
Имеем, 6х + 6у = 10х – 10у.
Отсюда получаем 4х = 16у, следовательно, х = 4у.
Подставим 4у вместо х в одно из выражений времени движения плота, имеем ![]()
Мы ответили на главный вопрос задачи: за 30 часов плот пройдёт расстояние от А до В.
Решим эту же задачу графическим способом.
Зададим координатную плоскость: по горизонтальной оси абсцисс будем отмечать время движения, по вертикальной оси ординат отметим расстояние АВ. По течению реки лодка прошла 6 часов, значит, изобразим движение лодки синим отрезком АС с концами в точках А(0; 0) и С(6; АВ).
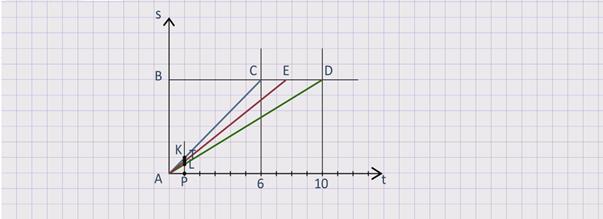
Против течения реки лодка прошла 10 часов, значит, изобразим движение лодки зелёным отрезком АD с концами в точках A(0; 0) и D(10; АВ). Рассмотрим на синей и зелёной линиях точки с абсциссой 1 и отметим их точками K и L соответственно. Точку на оси абсцисс с абсциссой 1 обозначим буквой Р. Таким образом, отрезок РК моделирует скорость движения лодки по течению, PL моделирует скорость движения лодки против течения.
Так как собственная скорость лодки есть среднее арифметическое между скоростями по течению и против течения реки, то линия собственного движения будет расположена между синей и зелёной линиями и будет являться медианой треугольника, образованного этими линиями и прямой х = 1. Обозначим середину отрезка КL точкой Т. Отрезок РТ моделирует собственную скорость движения лодки, Чтобы ответить на главный вопрос задачи, надо расстояние АВ поделить на скорость течения реки. Эта скорость моделируется на графикеравными отрезками КТ и ТL. Отрезки будут равны, так как они отражают разность скоростей по течению и собственной или разность скоростей собственной и против течения.
Отметим красным цветом отрезок АЕ с концами в точке А(0;0) и точке Е – точкой пересечения луча АЕ с прямой у = АВ, лежащий на отрезке АТ. Таким образом, время движения плота равно отношению длины отрезка АВ к длине отрезка КТ или АВ к длине отрезка TL, то есть

Чтобы найти длину отрезка KТ, надо найти полуразность скоростей по течению и против течения реки, а значит, полуразность длин отрезков РК и РL, то есть (РК – PL) : 2.
Так как АВ = 6РК = 10PL, то PL = 0,6PK. Имеем,
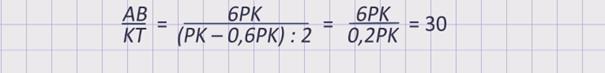
Получили, что плот пройдёт расстояние АВ за 30 часов.
Таким образом, на этом занятии мы решили одну и ту же задачу тремя различными способами и увидели, что ответ на главный вопрос задачи не зависит от способа её решения. Во всех трёх случаях мы получили один и тот же ответ.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 1. Катер движется против течения реки. За сколько часов он преодолеет расстояние 112 км, если его собственная скорость 30 км/ч, а скорость течения реки 2 км/ч?
Решение: Сначала узнаем скорость движения катера против течения реки, для этого от его собственной скорости отнимем скорость течения:
30 – 2 = 28 (км/ч) — скорость движения катера против течения.
Теперь можно узнать за сколько часов катер преодолеет 112 км, разделив расстояние на скорость:
112 : 28 = 4 (ч).
Решение задачи по действиям можно записать так:
1) 30 – 2 = 28 (км/ч) — скорость движения катера против течения,
2) 112 : 28 = 4 (ч).
Ответ: За 4 часа катер преодолеет расстояние 112 км.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.
Задача 2. Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Рассмотрите два варианта:
1) лодка движется по течению реки;
2) лодка движется против течения реки.
Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:
27 + 3 = 30 (км/ч).
Значит расстояние между пунктами лодка преодолеет за:
120 : 30 = 4 (ч).
Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:
27 – 3 = 24 (км/ч).
Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:
120 : 24 = 5 (ч).
Решение задачи по действиям для движения по течению реки можно записать так:
1) 27 + 3 = 30 (км/ч) — скорость лодки,
2) 120 : 30 = 4 (ч).
Для движения против течения реки решение задачи по действиям можно записать так:
1) 27 – 3 = 24 (км/ч) — скорость лодки,
2) 120 : 24 = 5 (ч).
Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.
Данный материал представляет собой систему
задач по теме “Движение”.
Цель: помочь учащимся более полно овладеть
технологиями решения задач по данной теме.
Задачи на движение по воде.
Очень часто человеку приходится совершать
движения по воде: реке, озеру, морю.
Сначала он это делал сам, потом появились плоты,
лодки, парусные корабли. С развитием техники
пароходы, теплоходы, атомоходы пришли на помощь
человеку. И всегда его интересовали длина пути и
время, затраченное на его преодоление.
Представим себе, что на улице весна. Солнце
растопило снег. Появились лужицы и побежали
ручьи. Сделаем два бумажных кораблика и пустим
один из них в лужу, а второй – в ручей. Что же
произойдет с каждым из корабликов?
В луже кораблик будет стоять на месте, а в
ручейке – поплывет, так как вода в нем “бежит”
к более низкому месту и несет его с собой. То же
самое будет происходить с плотом или лодкой.
В озере они будут стоять на месте, а в реке –
плыть.
Рассмотрим первый вариант: лужа и озеро. Вода в
них не движется и называется стоячей.
Кораблик поплывет по луже только в том случае,
если мы его подтолкнем или если подует ветер. А
лодка начнет двигаться в озере при помощи весел
или если она оснащена мотором, то есть за счет
своей скорости. Такое движение называют движением
в стоячей воде.
Отличается ли оно от движения по дороге? Ответ:
нет. А это значит, что мы с вами знаем как
действовать в этом случае.
Задача 1. Скорость катера по озеру равна 16 км/ч.
Какой путь пройдет катер за 3 часа?
Ответ: 48 км.
Следует запомнить, что скорость катера в
стоячей воде называют собственной скоростью.
Задача 2. Моторная лодка за 4 часа проплыла по
озеру 60 км.
Найдите собственную скорость моторной лодки.
Ответ: 15 км/ч.
Задача 3. Сколько времени потребуется лодке,
собственная скорость которой
равна 28 км/ч, чтобы проплыть по озеру 84 км?
Ответ: 3 часа.
Итак, чтобы найти длину пройденного пути,
необходимо скорость умножить на время.
Чтобы найти скорость, необходимо длину пути
разделить на время.
Чтобы найти время, необходимо длину пути
разделить на скорость.
Чем же отличается движение по озеру от
движения по реке?
Вспомним бумажный кораблик в ручье. Он плыл,
потому что вода в нем движется.
Такое движение называют движением по течению.
А в обратную сторону – движением против
течения.
Итак, вода в реке движется, а значит имеет свою
скорость. И называют ее скоростью течения реки.
( Как ее измерить?)
Задача 4. Скорость течения реки равна 2 км/ч. На
сколько километров река относит
любой предмет (щепку, плот, лодку) за 1час, за 4
часа?
Ответ: 2 км/ч, 8 км/ч.
Каждый из вас плавал в реке и помнит, что по
течению плыть гораздо легче, чем против течения.
Почему? Потому, что в одну сторону река
“помогает” плыть, а в другую – “мешает”.

Рис.1
Те же, кто не умеет плавать, могут представить
себе ситуацию, когда дует сильный ветер.
Рассмотрим два случая:
1) ветер дует в спину,
2) ветер дует в лицо.
И в том и в другом случае идти сложно. Ветер в
спину заставляет бежать, а значит, скорость
нашего движения увеличивается. Ветер в лицо
сбивает нас, притормаживает. Скорость при этом
уменьшается.
Остановимся на движении по течению реки. Мы уже
говорили о бумажном кораблике в весеннем ручье.
Вода понесет его вместе с собой. И лодка,
спущенная на воду, поплывет со скоростью течения.
Но если у нее есть собственная скорость, то она
поплывет еще быстрее.
Следовательно, чтобы найти скорость движения
по течению реки, необходимо сложить собственную
скорость лодки и скорость течения.
Задача 5. Собственная скорость катера равна 21
км/ч, а скорость течения реки 4 км/ч. Найдите
скорость катера по течению реки.
Ответ: 25км/ч.
Теперь представим себе, что лодка должна плыть
против течения реки. Без мотора или хотя бы весел,
течение отнесет ее в обратную сторону. Но, если
придать лодке собственную скорость ( завести
мотор или посадить гребца), течение будет
продолжать отталкивать ее назад и мешать
двигаться вперед со своей скоростью.
Поэтому, чтобы найти скорость лодки против
течения, необходимо из собственной скорости
вычесть скорость течения.
Задача 6. Скорость течения реки равна 3 км/ч, а
собственная скорость катера 17 км/ч.
Найдите скорость катера против течения.
Ответ: 14 км/ч.
Задача 7. Собственная скорость теплохода равна
47,2 км/ч, а скорость течения реки 4,7 км/ч. Найдите
скорость теплохода по течению и против течения.
Ответ: 51,9 км/ч; 42,5 км/ч.
Задача 8. Скорость моторной лодки по течению
равна12,4 км/ч. Найдите собственную скорость
лодки, если скорость течения реки 2,8 км/ч.
Ответ: 9,6 км/ч.
Задача 9. Скорость катера против течения равна
10,6 км/ч. Найдите собственную скорость катера и
скорость по течению, если скорость течения реки
2,7 км/ч.
Ответ: 13,3 км/ч; 16 км/ч.
Связь между скоростью по течению и
скоростью против течения.
Введем следующие обозначения:
Vс. – собственная скорость,
Vтеч. – скорость течения,
V по теч. – скорость по течению,
V пр.теч. – скорость против течения.
Тогда можно записать следующие формулы:
V no теч = Vc + Vтеч ;
V np. теч = Vc – V теч.;
Попытаемся изобразить это графически:
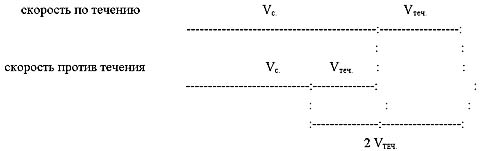
Рис. 2
Вывод: разность скоростей по течению
и против течения равна удвоенной скорости
течения.
Vno теч — Vnp. теч = 2 Vтеч.
Vтеч = (V по теч – Vnp. теч ): 2
Задача.
1) Скорость катера против течения равна 23 км/ч, а
скорость течения 4 км/ч.
Найдите скорость катера по течению.
Ответ: 31 км/ч.
2) Скорость моторной лодки по течению реки равна
14 км/ч/ а скорость течения 3 км/ч. Найдите скорость
лодки против течения
Ответ: 8 км/ч.
Задача 10. Определите скорости и заполните
таблицу:
|
V С. |
Vтеч. |
Vпо теч. |
Vпр.теч. |
|
|
1 |
12 км/ч |
3 км/ч |
||
|
2 |
23 км/ч |
25 км/ч |
||
|
3 |
24 км/ч |
20 км/ч |
||
|
4 |
4 км/ч |
17 км/ч: |
||
|
5 |
5 км/ч |
18 км/ч |
||
|
6 |
42 км/ч |
34 км/ч |
* – при решении п.6 смотри рис.2.
Ответ: 1) 15 и 9; 2) 2 и 21; 3) 4 и 28; 4) 13 и 9; 5)23 и 28; 6) 38 и 4.
