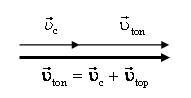Здравствуйте, Алексей!
Ваше решение совершенно верно. Однако есть некоторая небрежность в определении переносной скорости.
Вы складываете скорости разных точек (скорость течения точек воды относительно берега и скорость пловца , что совершенно недопустимо.
Переносной скоростью нельзя называть скорость движения системы отсчета, тем более при вращательном движении СО понятие скорости СО вообще исчезает, так как разные ее точки имеют разные скорости.
Итак, Vа=Vп+Vо (в формулах все величины векторные). С определением абсолютной и относительной скорости нет проблем. Так что же такое переносная скорость? Определение легко дать, исходя из самой формулы. Если Vо=0, то Vа=Vп. То есть переносная скорость это скорость точки в неподвижной системе, если в подвижной системе она покоится. Это скорость, с которой подвижная система переносит относительно неподвижной покоящуюся на ней точку. Потому она и называется переносной.
Из такого понятия и вытекает, что в нашем случая скорость течения реки и есть переносная скорость.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,912 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Условие
B8. Скорость пловца относительно воды 1,2 м/с. Скорость течения 0,8 м/с. Определите скорость пловца относительно берега, если пловец плывет по течению реки.
Решение
1 способ. Решим задачу по предложенному плану.
| План решения задач: | Решение |
|---|---|
| 1. Сделайте чертеж: тела изобразите в виде прямоугольников, над ними укажите направление скорости. |
Рис. 1 |
| 2. Выберите направление осей координат. | |
| 3. Исходя из условия задачи или по ходу решения: | |
| а) определите тело, скорость которого надо найти; | Пловец. |
| б) определите тело, с которым свяжем неподвижную СО; | Берег. |
| в) определите тело, с которым свяжем подвижную СО и объясните свой выбор; | Вода (течение), т.к. несмотря на то, что движутся два тела (пловец и вода), скорость пловца задана относительно воды. |
| г) найдите скорость системы и объясните свой выбор; | υc = υтечения = 0,8 м/с, т.к. это скорость тела, с которым мы связали подвижную систему. |
| д) найдите скорость тела относительно неподвижной СО и объясните свой выбор; | Это скорость пловца относительно берега, с которым мы связали неподвижную систему. По условию эту скорость нужно найти. |
| е) найдите скорость тела относительно подвижной СО и объясните свой выбор. | υtop = υпловца = 1,2 м/с, т.к. скорость пловца задана относительно воды, с которой мы связали подвижную систему. |
| 4. Запишите закон сложения скоростей в векторном виде. | (~vec upsilon_{ton} = vec upsilon_c + vec upsilon_{top}) |
| 5. Найдите искомые величины. |
Способ а. Найдем проекцию скоростей на ось 0X:
υton x = υc + υtop = υтечения +υпловца (рис. 1). Все скорости направлены вдоль оси, поэтому их проекции положительные. Способ б. Найдем векторную сумму скоростей. Из рисунка 2 видно, что значение υton = υc + υtop = υтечения +υпловца.
Рис. 2 Тогда υton x = 0,8 м/с + 1,2 м/с = 2,0 м/с. |
2 способ. Так как задана скорость пловца относительно воды (течения), то воспользуемся законом сложения скоростей в следующем виде[~vec upsilon_p = vec upsilon_t + vec upsilon_{p/t}] , где υp/t = 1,2 м/с – скорость пловца относительно воды (течения); υt = 0,8 м/с – скорость течения (воды); υp – скорость пловца относительно берега (неподвижной СО), по условию эту скорость нужно найти.
Тогда в проекции на ось 0Х:
υp x = υt + υp/t; υp x = 0,8 м/с + 1,2 м/с = 2,0 м/с.
-
Математика
Предыдущий вопрос
Следующий вопрос
marin1226
3 года назад
Ответ
Ответ дан
larisa210679
Ответ:
2м/с
Пошаговое объяснение:
Скорость пловца относительно берега= векторной сумме скоростей течения относительно берега и его относительно воды. v=v1+v2 ( векторно) . Так как он плывет по течению, то модуль скорости относительно берега= сумме модулей скоростей течения относительно берега и его собственной скорости относительно воды. v = v1+v2 . v = 1,5+0,5=2м/c.
Ответы и объяснения
- marin1226
Не тот ответ, который тебе нужен?
Найди нужный
Условие задачи:
Пловец переплывает реку по прямой, перпендикулярной берегу. Определить скорость течения, если скорость пловца относительно воды в два раза больше скорости течения. Модуль скорости пловца относительно берега равен 0,5 м/с.
Задача №1.7.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(upsilon_1=2 upsilon_0), (upsilon=0,5) м/с, (upsilon_0-?)
Решение задачи:
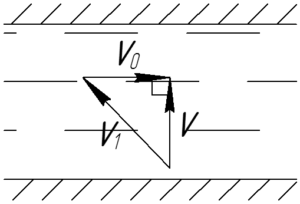Согласно правилу сложения скоростей, вектор скорости пловца относительно берега (overrightarrow upsilon) – это сумма вектора скорости пловца относительно реки (overrightarrow {{upsilon _1}}) и вектора скорости течения реки (overrightarrow {{upsilon _0}}).
[overrightarrow upsilon = overrightarrow {{upsilon _1}} + overrightarrow {{upsilon _0}} ]
Так как вектор скорости (overrightarrow upsilon) перпендикулярен берегу, то имеем следующий прямоугольный треугольник (смотри рисунок). Из теоремы Пифагора следует:
[upsilon _1^2 = {upsilon ^2} + upsilon _0^2]
По условию (upsilon_1=2 upsilon_0), поэтому:
[4upsilon _0^2 = {upsilon ^2} + upsilon _0^2]
[3upsilon _0^2 = {upsilon ^2} Rightarrow {upsilon _0} = frac{upsilon }{{sqrt 3 }}]
Выполним простой расчет и получим ответ.
[{upsilon _0} = frac{{0,5}}{{sqrt 3 }} = 0,29; м/с = 1,04; км/ч]
Ответ: 1,04 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.16 Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду
1.7.18 Пассажирский поезд идет со скоростью 72 км/ч. По соседнему пути движется
1.7.19 Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду
