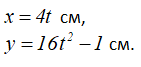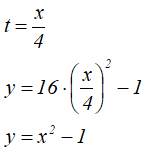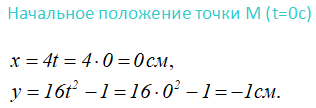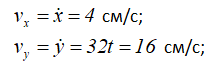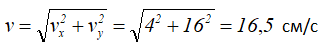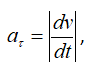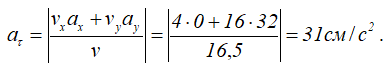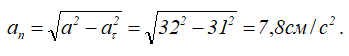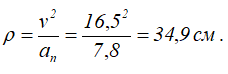Ответы Mail.ru
Образование
ВУЗы, Колледжи
Детские сады
Школы
Дополнительное образование
Образование за рубежом
Прочее образование
Вопросы – лидеры.
Как найти величину флуктуации сигнала на входе приемника если известно что
1 ставка
Помогите с математикой
Найдите сумму членов ряда
1 ставка
Выполнить расчет выпарной установки
1 ставка
Математика Помогите!
Найдите формулу общего члена ряда по его первым членам
1 ставка
Помогите решить задачи в Excel
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Григорий Еськин
Ученик
(187),
закрыт
13 лет назад
Лучший ответ
Vladimir Shchookin
Просветленный
(42070)
13 лет назад
V=[(Vx)^2+(Vy)^2]^1/2
GELAYU USPEHOV !!!
Vladimir Shchookin.
Остальные ответы
Q-vinsanti
Ученик
(92)
13 лет назад
Скорости если на плоскости то сложи а если в пространстве то как сумма векторов по правилу треугольника.
ZoNNda
Мудрец
(12128)
13 лет назад
как корень квадратный из суммы квадратов x и y.
Похожие вопросы
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
Прошу проверить и подсказать с графиком. Проверьте правильность вычислений и подскажите как построить нормальное и тангенсальное ускорения на графике.
|
||
| Вернуться к началу |
|
||
|
nexzis |
Заголовок сообщения: Re: кинематика точки
|
|
я и так и так искал просто написал по этой формуле что то я запутался)) если у меня ускорение по иксу = -3/32 а полное 3/32 то на графике они располагаются противоположно и как тогда располагаются нормальное и тангенциальное ускорения? ведь получается полное вправо параллельно иксу а нормальное должно быть внутрь кривизны…. кто может нарисовать график по значениям? а то получается что у меня нормальное усконие направлено не внутрь кривизны а вне её
|
|
| Вернуться к началу |
|
|
si2213 |
Заголовок сообщения: Re: кинематика точки
|
|
вся беда в том, что у вы ищете касательное ускорение по модулю, уберите модуль. Если полученное значение касательного ускорения будетиметь такой же знак как у скорости , то вектор касательного ускорения и вектор скорости совпадают по направлению, если знаки разные, то не совпадают. А нормальное ускорение всегда направленио внутрь траектории. кроме того проекция вектора ускорения на ось Х у вас отрицательная, по оси Y равна нулю, вот по этим проекциям и стройте вектор полного ускорения. А то , что нашли по пифагору, так это только модуль полного ускорения, направления пифагор не указывает.
|
|
| Вернуться к началу |
|
|
nexzis |
Заголовок сообщения: Re: кинематика точки
|
|
|
|
| Вернуться к началу |
|
|
nexzis |
Заголовок сообщения: Re: кинематика точки
|
|
спасибо, но я к сожалению не молодец, можете спросить у Валентины и lexus666 =) можете проверить ещё 1 задачку рисунок плохо получился
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти полную вариацию
в форуме Функциональный анализ, Топология и Дифференциальная геометрия |
lllulll |
1 |
703 |
10 окт 2015, 13:28 |
|
Найти полную вариацию функции
в форуме Функциональный анализ, Топология и Дифференциальная геометрия |
SashaKvint |
1 |
522 |
18 апр 2020, 09:50 |
|
Найти частную и полную производную по переменной x
в форуме Дифференциальное исчисление |
swimbo |
0 |
263 |
16 июн 2015, 12:25 |
|
Найти проекции векторов на оси OX и OY
в форуме Векторный анализ и Теория поля |
limitless |
4 |
132 |
08 дек 2022, 21:00 |
|
Найти длину проекции дуги
в форуме Аналитическая геометрия и Векторная алгебра |
AlexKey |
7 |
913 |
15 фев 2017, 20:05 |
|
Найти матрицу ортогональной проекции
в форуме Линейная и Абстрактная алгебра |
mattafix |
0 |
173 |
21 май 2018, 12:19 |
|
Найти координаты проекции и расстояние
в форуме Аналитическая геометрия и Векторная алгебра |
Anab0l1k |
2 |
374 |
19 дек 2013, 13:49 |
|
Найти длину проекции гипотенузы на плоскость
в форуме Геометрия |
Victoria1625 |
10 |
1917 |
06 мар 2014, 15:27 |
|
Найти 1ую главную компоненту и проекции выборки
в форуме Линейная и Абстрактная алгебра |
Knyazhe |
0 |
149 |
17 май 2020, 21:12 |
|
Построение скоростей, точек МЦС
в форуме Механика |
Shale |
8 |
425 |
10 апр 2017, 12:08 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Для описания движения используют три величины — скорость, время и расстояние. В координатном углу на горизонтальном луче отмечается время, на вертикальном — пройденное расстояние. Скорость объекта при равномерном движении можно вычислить.
Чтобы по графику движения определить скорость объекта (v), нужно узнать, какое расстояние (s) проходит объект за некоторое время (t), и найти частное расстояния и времени:
v=s:t
.
Для расчёта скорости можно взять любой удобный временной отрезок и пройденное за это время расстояние.
Пример:
по данному графику найти скорость движения объекта.
Решение.
(1) способ. За (1) час пройдено (8) км, то есть скорость объекта равна (8) км/ч.
(2) способ. За (5) часов пройдено (40) км, поэтому скорость объекта равна (40:5=8) км/ч.
Ответ: (8) км/ч.
При равномерном движении график представляет собой отрезок. И наоборот, в каждой точке отрезка скорость одинаковая.
Обрати внимание!
Чем больше скорость движения объекта, тем график круче.
Остановка в пути обозначается на графике движения горизонтальными отрезками, так как пройденное расстояние не меняется.
По данному графику движения можно определить, что с (9):(00) до (11):(00) была остановка в пути.
Источники:
Изображения: график движения. © ЯКласс.
Как определить скорость по графику?
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Как определить скорость тела при равномерном движении?
Скорость при прямолинейном движении — величина постоянная. Для того, чтобы найти скорость, необходимо пройденный путь разделить на время, за которое он был пройден.
Как составить уравнение скорости по графику?
График скорости График скорости — графическое представление уравнения скорости тела v = v(t). График v(t) служит для описания движение тела. На этом графике представлено равноУскоренное движение.
Что называется скоростью тела при равномерном движении?
Скорость при равномерном прямолинейном движении. Скорость и (м/с) — векторная физическая величина, которая показывает, какое перемещение совершает тело за единицу времени.
Как изменяется скорость тела при равномерном движении?
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0). Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Как составить уравнение движения тела?
х=х +vхt. Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х .
Как записать уравнение проекции скорости?
Зависимость проекции скорости движущегося тела от времени имеет вид: vx = 2 + 3t (м/с).
Как написать уравнение зависимости?
Уравнение зависимости скорости от времени при движении с ускорением имеет вид:
- v(t) = vo + at = 20 + 1.5t. Производная функции зависимости координаты от времени равна функции зависимости скорости от времени:
- x’ (t) = v (t). …
- x(t) = 0.75t 2 + 20t.
Как написать уравнение скорости по графику
Графическое представление равномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V (t) – изменение скорости со временем
S(t) – изменение перемещения (пути) со временем
a(t) – изменение ускорения со временем

За висимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v = const ), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) – прямая линия, параллельная оси времени.
Проекция перемещения тела численно равна площади прямоугольника АОВС под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.
Зависимость перемещения от времени. График s(t) – наклонная линия :
Из графика видно, что проекция скорости равна:
Рассмотрев эту формулу, мы можем сказать, чем больше угол, тем быстрей движется тело и оно проходит больший путь за меньшее время.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Неравномерное прямолинейное движение.
Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.
Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным или переменным движением.
Для характеристики неравномерного движения вводится понятие средней скорости.
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.
Различие между средней и мгновенной скоростями показано на рисунке.
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.
Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
Vx — Скорость тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
ax — Ускорение тела
t — Время движения тела
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.
Единица измерения ускорения в СИ [м/с 2 ].
Ускорение измеряют акселерометром
Уравнение скорости для равноускоренного движения: vx = vxo + axt
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):
Sx — Перемещение тела при равноускоренном движении по прямой
Vx o — Начальная скорость тела
Vx — Скорость тела при равноускоренном движении по прямой
ax — Ускорение тела
t — Время движения тела
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:
– если известны начальная, конечная скорости движения и ускорение.
– если известны начальная, конечная скорости движения и время всего движения
Графическое представление неравномерного прямолинейного движения
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:
V(t) – изменение скорости со временем
S(t) – изменение перемещения (пути) со временем
a(t) – изменение ускорения со временем
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.
Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости vx = vxo + axt . Графиком является наклонная линия.
Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.
Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости:
В координатах зависимость имеет вид:
Уравнение движения, графики равномерного прямолинейного движения
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.
Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end
Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
 |
Построим графики зависимости координаты от времени для нашего примера: |
x=20+10t – машина движется вправо (в направлении оси OX)
x=20-10t – машина движется влево (в направлении, противоположном оси OX)
x=20 – машина стоит
п.5. Как найти уравнение движения по графику движения?
п.6. График скорости vx=vx(t)
Для рассмотренного примера:
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:
По графику находим: begin x_1=x(5)=8cdot 5=40 text<(м)>\ x_2=x(10)=8cdot 10=80 text <(м)>end
б) Скорость (v_x=8) м/с – постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text <(м)>$$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac=frac<56-38><2-1>=18 (text<тыс.км/ч>) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text<тыс.км/ч>) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text<тыс.км>) $$
г) Переведем скорость в км/с: $$ 18000frac<text<км>><text<ч>>=frac<18000 text<км>><1 text<ч>>=frac<18000 text<км>><3600 text>=5 text <км/c>$$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
[spoiler title=”источники:”]
http://www.sites.google.com/site/opatpofizike/teoria/teoria-10-klass/graficeskoe-predstavlenie-dvizenia
http://reshator.com/sprav/fizika/7-klass/uravnenie-dvizheniya-grafiki-ravnomernogo-pryamolinejnogo-dvizheniya/
[/spoiler]
Решение задачи (РГР) К1 «Определение скорости и ускорения точки по заданным уравнениям ее движения» по разделу «кинематика» теоретической механики.
Пример определения для заданного момента времени положения точки на траектории, скорости, полного, касательного и нормального ускорения, радиуса кривизны траектории и вида траектории движения точки, если движение точки задано уравнениями.
Задача
Движение точки M задано уравнениями:
Требуется:
Установить вид траектории движения точки M, и для момента времени t = t1 = 0,5 с найти:
- положение точки на траектории,
- скорость, полное, касательное и нормальное ускорения,
- радиус кривизны траектории.
Другие примеры решений >
Помощь с решением задач >
Решение
Расчет траектории движения точки
Уравнения движения можно рассматривать как параметрические уравнения траектории точки.
Другие видео
Чтобы узнать вид траектории в координатной форме, надо получить прямую зависимость между переменными x и y, для этого избавимся от параметра времени t, выразив его, например, из первого уравнения и подставив во второе.
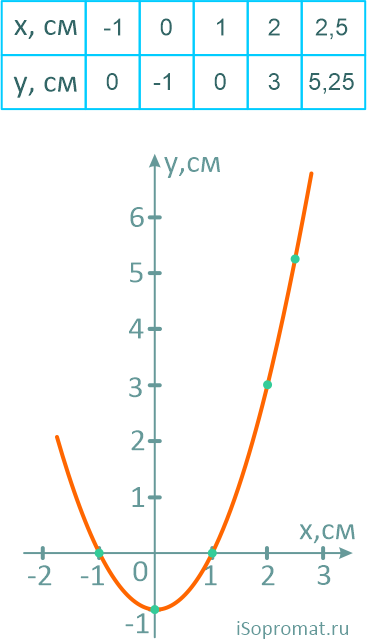
Получилось квадратное уравнение. То есть точка движется по параболе.
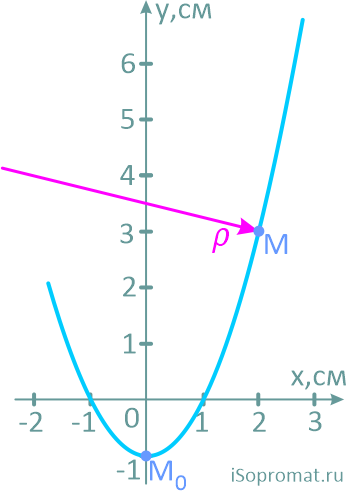
Построим траекторию движения, рассчитав несколько её точек.
Положение точки на траектории
Определим положения точки в начале движения и в заданный момент времени.
Для этого в исходные уравнения подставляем соответственно сначала 0
а затем, половину секунды.
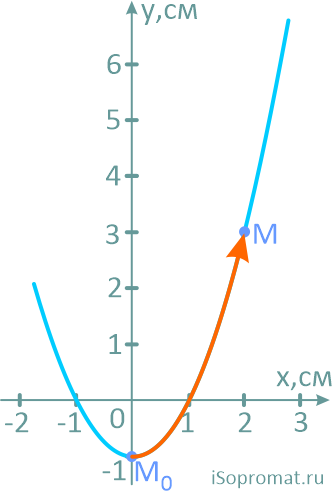
Положение точки на ее траектории в заданный момент обозначим буквой M, и все остальные параметры будем рассчитывать для неё.
Расчет скорости точки
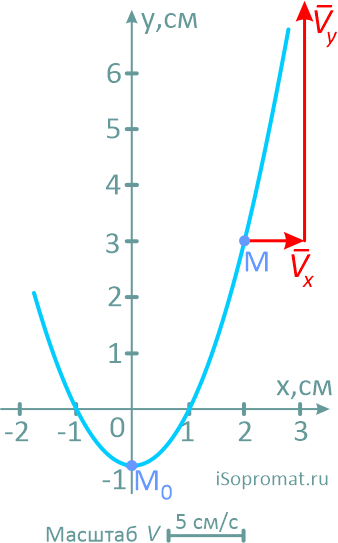
Направление и величину скорости точки определим как векторную сумму её проекций на оси координат.
Здесь i, j — орты осей x и y.
vx, vy — проекции вектора скорости на оси координат.
Проекции вектора скорости получим, взяв первые производные по времени t от соответствующих заданных уравнений движения точки.
Далее выбрав масштаб, из точки M последовательно и с учетом знака, откладываем оба вектора.
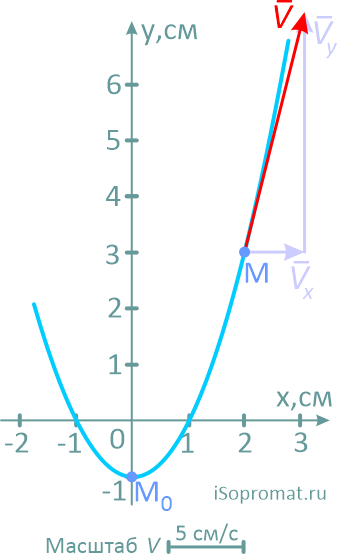
Сам вектор скорости получим, соединив точку M с концом второго вектора и направив его по ходу движения точки.
Здесь надо отметить, что вектор скорости всегда должен располагаться по касательной к траектории. Любое другое положение будет указывать на ошибки в расчетах.
Рассчитаем модуль вектора скорости
Расчет ускорений точки
Проекции полного ускорения точки на оси координат определяются как вторая производная от исходных уравнений движения точки.
Здесь, ax, ay – проекции ускорения точки на оси координат.
В этом примере, горизонтальная проекция ускорения оказалась равной нулю, поэтому его модуль и направление будут совпадать с вертикальной.
Касательная составляющая полного ускорения это производная скорости точки по времени.
Ее можно рассчитать по этой формуле.
Вектор касательного ускорения всегда направлен по линии вектора скорости.
Положительная величина говорит об ускоренном движении точки и тогда направления скорости и касательного ускорения совпадают.
В противном случае они разнонаправлены, и движение точки замедляется.
Модуль нормального ускорения определим по формуле Пифагора, так как векторы касательного и центростремительного ускорений всегда взаимно перпендикулярны.
Расчет радиуса кривизны траектории
Осталось найти только радиус кривизны траектории в точке M, который равен отношению квадрата скорости к модулю нормального ускорения.
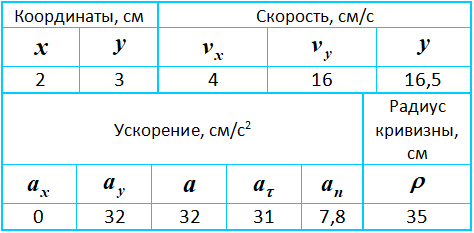
Результаты расчетов
Результаты вычислений для заданного момента времени t1=0,5c приведены в таблице:
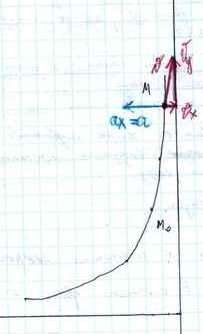
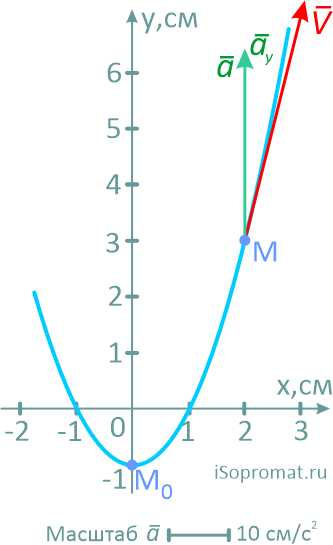
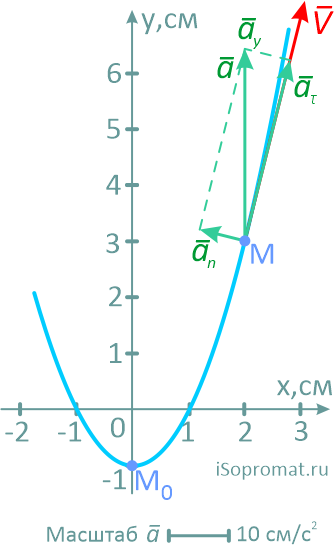
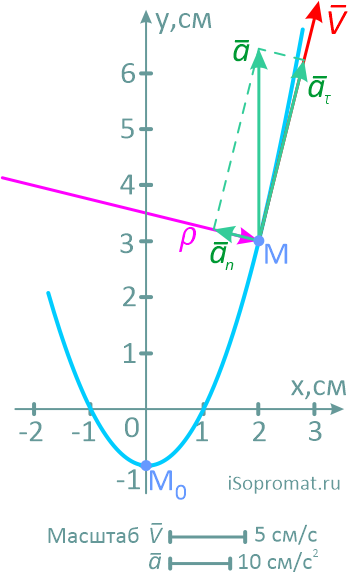
На рисунке показано положение точки M в заданный момент времени и векторы скорости и ускорений в выбранном масштабе.
Вектор v строим по составляющим vx и vy, причем этот вектор должен по направлению совпадать с касательной к траектории.
Вектор a строим по составляющим ax и ay и затем раскладываем на составляющие векторы aτ и an. Совпадение величин aτ и an, найденных из чертежа, с их значениями, полученными аналитически, служит критерием правильности решения.
Другие примеры решения задач >