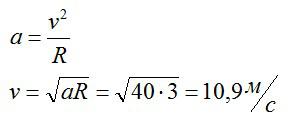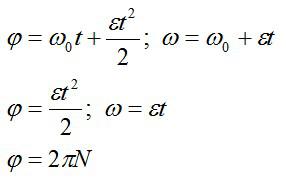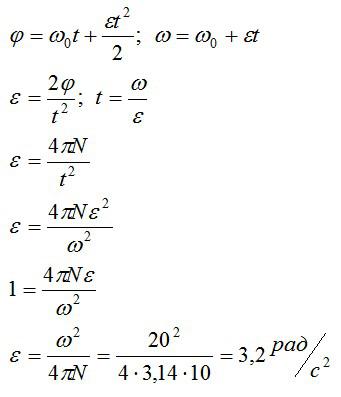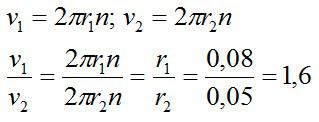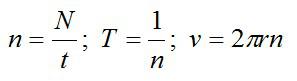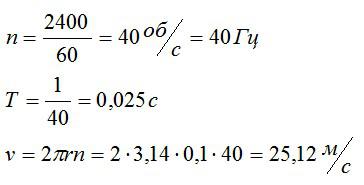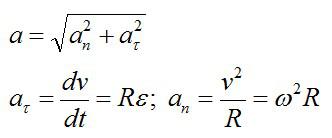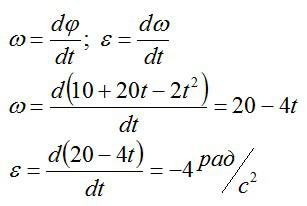Как найти скорость по круговой траектории - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 ноября 2016 года; проверки требуют 5 правок.

О разновидности перекрёстков: см. Круговой перекрёсток.

В физике кругово́е движе́ние — это вращательное движение материальной точки или тела, когда ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела. В этом случае траектория точки или тела является окружностью, круговой орбитой. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение.

Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма.

Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона.

Формулы для равномерного кругового движения[править | править код]

Рис. 1: Взаимосвязи векторов равномерного кругового движения; вектор Ω, представляющий вращение, перпендикулярен к плоскости орбиты.

Для движения по кругу радиуса R длина окружности будет C = 2π R. Если период вращения есть T, то угловая скорость вращения ω будет равна:

$omega ={frac {2pi }{T}} .$

Скорость движения объекта равна

$v,={frac {2pi R}{T}}=omega R$

Угол поворота θ за время t равен:

${displaystyle theta =2pi {frac {t}{T}}=omega t}$

Ускорение, вызванное изменением направления скорости, можно найти, если заметить, что скорость совершает полное изменение направления за то же самое время T, за которое объект делает один оборот. Тогда вектор скорости проходит путь длиной 2π v каждые T секунд, или:

$a,={frac {2pi v}{T}}=omega ^{2} R ,$

и направлено радиально к центру.

Взаимосвязи векторов показаны на рис. 1. Ось вращения изображена вектором Ω, перпендикулярно плоскости орбиты и имеет величину ω = dθ / dt. Направление вектора Ω выбрано в соответствии с правилом правой руки. По этому соглашению скорость это векторное произведение вида:

{mathbf {v}}={boldsymbol Omega }times {mathbf r} ,

и есть вектор, перпендикулярный как Ω так и r ( t ), направленный по касательной к орбите и имеющий величину ω R. Аналогично, ускорение определяется как:

{mathbf {a}}={boldsymbol Omega }times {mathbf v} ,

Оно представляет собой вектор, перпендикулярный как Ω так и v ( t ), имеющий величину ω |v| = ω² R и направление строго противоположно к r ( t ).

Постоянная скорость[править | править код]

В простейшем случае скорость, масса и радиус являются постоянными.

Рассмотрим тело массой один килограмм, движущееся по кругу радиуса один метр с угловой скоростью один радиан в секунду.

Теперь рассмотрим тело массы , движущееся по кругу радиуса с угловой скоростью

Переменная скорость[править | править код]

В круговом движении полную силу, приложенную к объекту, можно разложить на две составляющие: центростремительную, удерживающую тело на круговой орбите (т. е. меняющую направление вектора скорости), и тангенциальную, направленную по касательной к окружности и вызывающую изменение длины вектора скорости (т. е. меняющую скорость вращения тела по орбите). Величина центростремительной составляющей зависит от мгновенной скорости.

Для примера, когда камень привязан к концу верёвки, то он подвергается воздействию некоторой силы, которую мы можем разложить на радиальную и боковую составляющие. Радиальная направлена к центру (вовнутрь) окружности и вызвана тем, что веревка сопротивляется удлинению. А боковая составляющая определяет будет вращение камня ускоряться или замедляться.

Описание кругового движения в полярных координатах[править | править код]

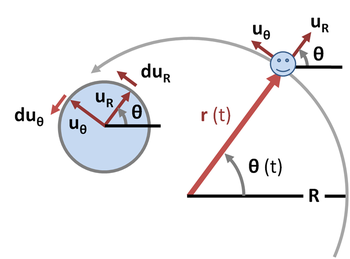
Траектория кругового движения тела может быть описана в полярной системе координат значениями фиксированного расстояние R от центра орбиты, являющейся точкой отсчёта, и угла ориентации θ (t) от некоторого фиксированного направления (рис. 2). Вектор перемещения является радиальным вектором от полюса до текущего положения:

${vec r}=R{hat u}_{R}(t) ,$

где ${hat u}_{R}(t)$ — единичный вектор, параллельный радиусу в момент t и направленный от полюса. Удобно также ввести единичный вектор, ортогональный к ${hat u}_{R}$ , который назовём ${hat u}_{theta }$ . Обычно его ориентация выбирается по направлению движения вдоль орбиты.

Скорость является производной перемещения по времени:

${vec v}={frac {d}{dt}}{vec r}(t)={frac {dR}{dt}}{hat u}_{R}+R{frac {d{hat u}_{R}}{dt}} .$

Поскольку радиус окружности является константой, радиальная составляющая скорости равна нулю. Единичный вектор ${hat u}_{R}$ имеет инвариантное по времени значение, так что при изменении времени его конец всегда лежит на окружности единичного радиуса, а угол θ такой же, как у . Если произошло малое приращение угла dθ за время dt, тогда ${hat u}_{R}$ описывает дугу единичной окружности со значением dθ (см. единичную окружность слева на рис. 2). Следовательно:

${frac {d{hat u}_{R}}{dt}}={frac {dtheta }{dt}}{hat u}_{theta } ,$

где направление изменения должно быть перпендикулярно к ${hat u}_{R}$ (или, другими словами, вдоль ${hat u}_{theta }$ ), поскольку любое изменение d ${hat u}_{R}$ в направлении ${hat u}_{R}$ будет изменять величину ${hat u}_{R}$ . Знак положительный, потому что увеличение dθ влияет на объект и ${hat u}_{R}$ передвигается в направлении ${hat u}_{theta }$ .
Следовательно, скорость становится:

${vec v}={frac {d}{dt}}{vec r}(t)=R{frac {d{hat u}_{R}}{dt}}=R{frac {dtheta }{dt}}{hat u}_{theta } =Romega {hat u}_{theta } .$

Ускорение тела также можно разложить на радиальную и тангенциальную составляющие. Ускорение есть производная скорости по времени:

${vec a}={frac {d}{dt}}{vec v}={frac {d}{dt}}left(R omega {hat u}_{theta } right) .$

$=Rleft({frac {domega }{dt}} {hat u}_{theta }+omega {frac {d{hat u}_{theta }}{dt}}right) .$

Производная по времени от ${hat u}_{theta }$ находится таким же путём, как и для ${hat u}_{R}$ . Опять же, ${hat u}_{theta }$ есть единичный вектор, и его конец расположен на единичной окружности, а угол равен π/2 + θ. Следовательно, приращение угла dθ вектора перемещает ${hat u}_{theta }$ по дуге на величину dθ, и поскольку ${hat u}_{theta }$ перпендикулярен к ${hat u}_{R}$ , мы имеем:

${frac {d{hat u}_{theta }}{dt}}=-{frac {dtheta }{dt}}{hat u}_{R}=-omega {hat u}_{R} ,$

где отрицательный знак необходим, чтобы сохранить ${hat u}_{theta }$ перпендикулярным к ${hat u}_{R}$ . (Иначе угол между ${hat u}_{theta }$ и ${hat u}_{R}$ будет уменьшаться с увеличением dθ, см. единичную окружность слева на рис. 2). Следовательно, ускорение равно:

${vec a}=Rleft({frac {domega }{dt}} {hat u}_{theta }+omega {frac {d{hat u}_{theta }}{dt}}right)$

$=R{frac {domega }{dt}} {hat u}_{theta }-omega ^{2}R {hat u}_{R} .$

Центростремительное ускорение — это радиальная составляющая, направленная по радиусу вовнутрь:

${vec a}_{R}=-omega ^{2}R{hat u}_{R} ,$

тогда как тангенциальная составляющая изменяет значение скорости:

${vec a}_{{theta }}=R{frac {domega }{dt}} {hat u}_{theta }={frac {dRomega }{dt}} {hat u}_{theta }={frac {d|{vec v}|}{dt}} {hat u}_{theta } .$

Описание кругового движения в комплексных числах[править | править код]

Круговое движение можно описать с использованием комплексных чисел. Пусть — ось вещественных чисел, а — ось мнимых чисел. Тогда положение тела может быть задано в виде комплексного “вектора” :

$z=x+iy=R(cos theta +isin theta )=Re^{{itheta }} ,$

где есть мнимая единица, и

есть угол комплексного вектора по отношению к вещественной оси как функция времени t.
Поскольку радиус есть константа:

где точка означает дифференциал по времени.
В этих обозначениях скорость имеет вид :

${displaystyle v={dot {z}}=R{frac {d}{dt}}left(itheta right)e^{itheta }=iR{dot {theta }}e^{itheta }=iomega cdot Re^{itheta }=iomega z}$

а ускорение:

$a={dot v}=i{dot omega }z+iomega {dot z}=(i{dot omega }-omega ^{2})z$

$=left(i{dot omega }-omega ^{2}right)Re^{{itheta }}$

$=-omega ^{2}Re^{{itheta }}+{dot omega }e^{{i{frac {pi }{2}}}}Re^{{itheta }} .$

Первое слагаемое направлено против вектора перемещения, а второе — перпендикулярно ему, как и в предыдущих результатах.

Ссылки[править | править код]

BIGS animation (англ.) Круговое движение
Circular Motion (англ.) – глава из онлайн-учебника

См. также[править | править код]

Момент импульса
Уравнения движения
Математический маятник
Центростремительная сила
Сила инерции

Источник

Понятия и определения

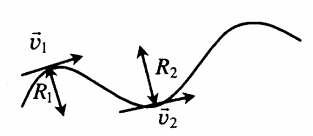
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

Траектория движения тела есть окружность.
Вектор скорости всегда направлен по касательной к окружности.
Направление скорости постоянно меняется под действием центростремительного ускорения.
Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Определение и формулы

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Определение и формулы

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Полезные факты

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Определение и формула

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с²). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10³ секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10⁶. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Задание EF18273

Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно…

Алгоритм решения

Записать исходные данные.
Записать формулу для определения искомой величины.
Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

Радиус окружности, по которой движется автомобиль: R = 100 м.
Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Ответ: 4

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17763

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза
б) уменьшить в 2 раза
в) увеличить в 4 раза
г) уменьшить в 4 раза

Алгоритм решения

Записать исходные данные.
Определить, что нужно найти.
Записать формулу зависимости центростремительного ускорения от частоты.
Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Радиус окружности R₁ = R.
Радиус окружности R₂ = 4R.
Центростремительное ускорение: a_ц.с.= a₁ = a₂.

Найти нужно ν₂.

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Или:

Отсюда:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 21.9k

Источник

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*

Источник

I. Механика

Тестирование онлайн

Угловая скорость

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Центростремительное ускорение

Используя предыдущие формулы, можно вывести следующие соотношения

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Особенности движения по окружности с постоянной по модулю скоростью:

Траектория движения тела есть окружность.
Вектор скорости всегда направлен по касательной к окружности.
Направление скорости постоянно меняется под действием центростремительного ускорения.
Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Линейная и угловая скорости

Линейная скорость

l — длина траектории, вдоль которой двигалось тело за время t

R — радиус окружности, по которой движется тело

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

Записать исходные данные.
Записать формулу для определения искомой величины.
Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

Радиус окружности, по которой движется автомобиль: R = 100 м.
Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

Записать исходные данные.
Определить, что нужно найти.
Записать формулу зависимости центростремительного ускорения от частоты.
Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Мгновенная и средняя скорость

Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.

Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.

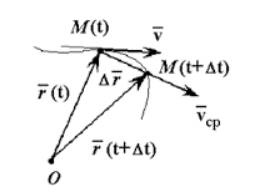
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения ” open=” υ = ∆ r ∆ t ; ” open=” υ ↑ ↑ ∆ r .

Рисунок 1 . Средняя скорость сонаправлена перемещению

Модуль средней скорости по пути равняется ” open=” υ = S ∆ t .

Мгновенная скорость точки. Формулы

Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.

Мгновенной скоростью называют предел, к которому стремится средняя скорость ” open=” υ при стремлении промежутка времени ∆ t к 0 :

υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ .

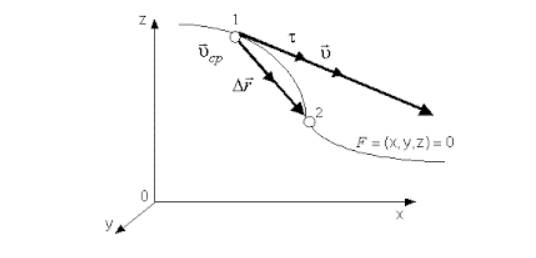
Направление вектора υ идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение d r совпадает с бесконечно малым элементом траектории d s .

Рисунок 2 . Вектор мгновенной скорости υ

Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:

υ x = d x d t = x ˙ υ y = d y d t = y ˙ υ z = d z d t = z ˙ .

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

υ = υ = υ x 2 + υ y 2 + υ z 2 = x 2 + y 2 + z 2 .

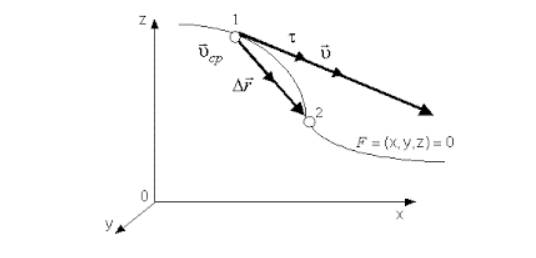
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r = r q 1 , q 2 , q 3 , тогда значение скорости запишется как:

υ = d r d t = ∑ i = 1 3 ∂ r ∂ q i ∂ q i ∂ r = ∑ i = 1 3 ∂ r ∂ q i q ˙ i .

Рисунок 3 . Перемещение и мгновенная скорость в системах криволинейных координат

При сферических координатах предположим, что q 1 = r ; q 2 = φ ; q 3 = θ , то получим υ , представленную в такой форме:

υ = υ r e r + υ φ e φ + υ θ φ θ , где υ r = r ˙ ; υ φ = r φ ˙ sin θ ; υ θ = r θ ˙ ; r ˙ = d r d t ; φ ˙ = d φ d t ; θ ˙ = d θ d t ; υ = r 1 + φ 2 sin 2 θ + θ 2 .

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t

Дан закон прямолинейного движения точки x ( t ) = 0 , 15 t 2 – 2 t + 8 . Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

υ ( t ) = x ˙ ( t ) = 0 . 3 t – 2 ; υ ( 10 ) = 0 . 3 × 10 – 2 = 1 м / с .

Ответ: 1 м / с .

Движение материальной точки задается уравнением x = 4 t – 0 , 05 t 2 . Вычислить момент времени t о с т , когда точка прекратит движение, и ее среднюю путевую скорость ” open=” υ .

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ ( t ) = x ˙ ( t ) = 4 – 0 , 1 t .

4 – 0 , 1 t = 0 ; t о с т = 40 с ; υ 0 = υ ( 0 ) = 4 ; ” open=” υ = ∆ υ ∆ t = 0 – 4 40 – 0 = 0 , 1 м / с .

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется 0 , 1 м / с .

[spoiler title=”источники:”]

Движение по окружности с постоянной по модулю скоростью

http://zaochnik.com/spravochnik/fizika/kinematika/mgnovennaja-i-srednjaja-skorost/

[/spoiler]

Источник

Лень разбираться с решением задач? Добро пожаловать к нам в телеграм, где собрана интересная и полезная информация для учащихся и не только.

Движение по окружности: определение, примеры

Движение по окружности – самый простой случай криволинейного движения.

Примеры движения по окружности:

грузовик движется по мосту с радиусом кривизны R;
атлет крутит шар в руке, перед тем как бросить его;
космическая станция летает по кругу над поверхностью Земли;
катафот вращается на раскрученном колесе велосипеда.

Приведем ниже кинематические соотношения для поступательного и вращательного движений:

Вопросы на движение по окружности

Вопрос 1. Как направлено центростремительное ускорение?

Ответ. Центростремительное ускорение направлено по радиус-вектору к центру окружности.

Вопрос 2. Велосипед катится по прямой. Как можно описать движение точки на ободе его колеса? Является ли это движение движением по окружности?

Ответ. Это одновременно поступательное движение и движение по окружности. Траекторией такого движения будет спираль.

Вопрос 3. Как направлено ускорение, если тело движется по окружности неравномерно?

Ответ. В таком случае к центростремительному (или нормальному) ускорению добавляется тангенциальное ускорение, направленное по касательной к окружности. Полное ускорение тела представляет собой векторную сумму тангенциального и нормального ускорений.

Вопрос 4. Что такое линейная и угловая скорость?

Ответ. Линейная скорость – это скорость точки, движущейся поступательно. Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.

Вопрос 5. При поступательном движении мерой инерции является масса. А что является мерой инерции при вращательном движении?

Ответ. При вращательном движении мерой инерции является момент инерции. Это отдельная обширная тема, задачи на нахождение и использование момента инерции рассмотрены в других статьях по физике.

Задачи на движение по окружности

Как решать задачи на движение по окружности? Так же, как и все остальные! Для начала, вот памятка по решению физических задач и полезный список формул. Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.

Задача №1. Нахождение линейной скорости при движении по окружности

Условие

Тело движется по окружности с ускорением 3 метра на секунду в квадрате по окружности радиусом 40 метров. Какова линейная скорость тела?

Решение

В данном случае ввиду имеется нормальное ускорение. Поэтому, для решения достаточно вспомнить всего одну формулу:

Ответ: 10,9 м/с.

Задача №2. Нахождение углового ускорения

Условие

Колесо, вращаясь с постоянным ускорением, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

Решение

Запишем закон вращения, учитывая, что по условию начальная угловая скорость равна нулю:

Выразим угловое ускорение из первого уравнения, а время – из второго. Затем подставим выраженное время в выражение для ускорения и сократим:

Ответ: 3,2 радиан на секунду в квадрате.

Чтобы перевести угол из радианов в градусы достаточно запомнить соотношение: в одном полном обороте 2пи радиан, или 360 градусов. Следовательно, в одном радиане примерно 57,3 градуса.

Задача №3. Нахождение скорости движения по окружности

Условие

Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?

Решение

Две точки вращаются на одном колесе, а значит, с одинаковой частотой. Используем соотношения для скорости:

Ответ: скорость точки на ободе больше в 1,6 раза.

Задача №4. Нахождение периода и частоты при движении по окружности

Условие

Маховик равномерно вращается и за время t=1 мин совершает N=2400 оборотов. Какова частота вращения маховика, период обращения и линейная скорость точки, расположенной на расстоянии 10 сантиметров от центра маховика?

Решение

По определению:

Подставим значения, предварительно переведя все величины в систему СИ, и вычислим:

Ответ: 40 Гц; 0,025 с; 25,12 м/с.

Задача №5. Нахождение полного ускорения при движении по окружности

Условие

Тело вращается вокруг стационарной оси по закону фи=10+20t-2t^2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.

Решение

Полное ускорение – векторная сумма нормального и тангенциального ускорений.

Вспоминаем, что скорость и ускорение можно вычислить через производные, зная закон движения:

Подставляем значение t из условия и вычисляем:

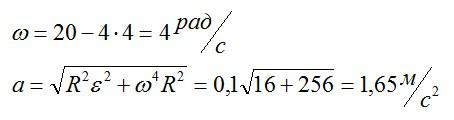
Задача №5. Нахождение полного ускорения при движении по окружности

Ответ: 1,65 метра в секунду.

Нужна помощь в выполнении заданий? Обращайтесь в профессиональный студенческий сервис в любое время.

Источник

Формулы для равномерного кругового движения[править | править код]

Постоянная скорость[править | править код]

Переменная скорость[править | править код]

Описание кругового движения в полярных координатах[править | править код]

Описание кругового движения в комплексных числах[править | править код]

Ссылки[править | править код]

См. также[править | править код]

Период, частота и количество оборотов

Линейная и угловая скорости

Линейная скорость

Угловая скорость

Центростремительное ускорение

I. Механика

Тестирование онлайн

Угловая скорость

Период и частота

Линейная скорость

Центростремительное ускорение

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*

I. Механика

Тестирование онлайн

Угловая скорость

Период и частота

Линейная скорость

Центростремительное ускорение

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Период, частота и количество оборотов

Линейная и угловая скорости

Линейная скорость

Угловая скорость

Центростремительное ускорение

Мгновенная и средняя скорость

Мгновенная скорость точки. Формулы

Перемещение и мгновенная скорость

Движение по окружности: определение, примеры

Вопросы на движение по окружности

Задачи на движение по окружности

Задача №1. Нахождение линейной скорости при движении по окружности

Задача №2. Нахождение углового ускорения

Задача №3. Нахождение скорости движения по окружности

Задача №4. Нахождение периода и частоты при движении по окружности

Задача №5. Нахождение полного ускорения при движении по окружности

Вам также может понравиться

Ammyy admin error 12029 как исправить

Как найти игрока для взвода

Как найти сопротивление формула p i2r

Добавить комментарий Отменить ответ