Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 марта 2018 года; проверки требуют 2 правки.
Мгнове́нный центр скоросте́й — при плоскопараллельном движении абсолютно твёрдого тела точка, связанная с этим телом, которая имеет следующие свойства: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело. Она существует в любой момент времени, но её положение меняется со временем за исключением одного случая — вращательного движения.
Положение мгновенного центра скоростей[править | править код]
Рис. 1. При качении колеса по горизонтальной дороге мгновенный центр скоростей находится в точке касания колеса и дороги — в точке А. 


Для того, чтобы определить положение мгновенного центра скоростей, необходимо знать направления скоростей любых двух различных точек тела, скорости которых не параллельны. Тогда для определения положения мгновенного центра скоростей необходимо провести перпендикуляры к прямым, параллельным линейным скоростям выбранных точек тела. В точке пересечения этих перпендикуляров и будет находиться мгновенный центр скоростей.
В том случае, если векторы линейных скоростей[1] двух различных точек тела параллельны друг другу, и отрезок, соединяющий эти точки, не перпендикулярен векторам этих скоростей, то перпендикуляры к этим векторам также параллельны. В этом случае говорят, что мгновенный центр скоростей находится в бесконечности, и тело движется мгновенно поступательно.
Если известны скорости двух точек, и эти скорости параллельны друг другу, и кроме того, указанные точки лежат на прямой, перпендикулярной скоростям, то положение мгновенного центра скоростей определяется так, как показано на рис. 2.
Положение мгновенного центра скоростей в общем случае не совпадает с положением мгновенного центра ускорений. Однако в некоторых случаях, например, при чисто вращательном движении, положения этих двух точек могут совпадать.

Рис. 2. Векторы скоростей точек колеса, лежащих на прямой РМ, образуют подобные треугольники; мгновенный центр скоростей находится в точке Р
Более общий случай сферического движения[править | править код]
Согласно теореме вращения Эйлера, любое вращающееся трёхмерное тело, имеющее неподвижную точку, также имеет и ось вращения. Таким образом, в более общем случае вращения трёхмерного тела говорят о мгновенной оси вращения.

Рис. 3. Чтобы определить положение мгновенного центра скоростей для шатуна в кривошипно-шатунном механизме, обычно необходимо провести перпендикуляры к векторам скоростей концов шатуна; мгновенный центр скоростей обозначен как CIR
Пример решения задачи[править | править код]
Найдём скорость точки K для колеса, показанного на рисунке 1, если задана скорость центра колеса (точки С), его радиус и угол АСК:



Решение
Найдём сначала угловую скорость колеса в данный момент времени при его вращении вокруг мгновенного центра скоростей (вокруг точки А):

Теперь, зная угловую скорость, найдём скорость точки К:

Чтобы найти численное значение 

или, учтя, что 

Вынесем R за знак корня:

Подставив заданые в условии численные значения, найдём:

Тогда, зная расстояние КА, можем найти численное значение скорости 

Ответ: 
Заметим, что для решения задачи знать численное значение R не обязательно.
Действительно, подставляя в формулу (*) выражения для 

Применение понятия мгновенного центра скоростей[править | править код]
Данное понятие используется при анализе движения звеньев кривошипно-шатунного механизма (рис. 3). Например, если известна постоянная угловая скорость вращающегося кривошипа (на рисунке 3 показан красным цветом), то скорость поршня не будет постоянной по модулю. Чтобы вычислить скорость поршня в разных положениях и построить соответствующий график, можно воспользоваться понятием мгновенного центра скоростей[2]. В свою очередь кривошипно-шатунные механизмы применяются в двигателях внутреннего сгорания, поршневых насосах, поворотных гидродвигателях и многих других устройствах. Таким образом, использование понятия мгновенного центра скоростей позволяет производить расчёты, необходимые для выбора оптимальной конструкции указанных механизмов.
Движения коленного, локтевого, плечевого и др. суставов биофизики также исследуют с помощью мгновенного центра скоростей.
Улучшения тормозных характеристик автомобилей можно добиться путём выбора оптимальной конструкции педалей тормоза и соответствующих кинематических расчётов, проведённых с помощью мгновенного центра скоростей.
Примечания[править | править код]
- ↑ Показанные на рис. 1 скорости являются линейными
- ↑ Скорости поршня в разных положениях можно также рассчитать графически с помощью плана скоростей
Литература[править | править код]
- Тарг С. М. Краткий курс теоретической механики. Учеб. для втузов.— 10-е изд., перераб. и доп. — М.: Высш. шк., 1986.— 416 с, ил.
- Основной курс теоретической механики (часть первая) Н. Н. Бухгольц, изд-во «Наука», Главная редакция физико-математической литературы, Москва, 1972, 468 стр.

Рассмотрим формулы и примеры определения положения мгновенного центра скоростей (МЦС) для различных твердых тел и механизмов при плоскопараллельном движении.
Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.
В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю.
Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
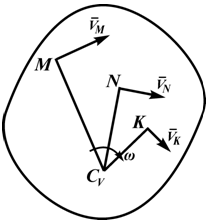
Рисунок 2.16
При определении положения МЦС скорость любой точки может быть записана: VM = VCv + VMCv , где точка CV выбрана за полюс. Поскольку это МЦС и VCv=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей:
VM=VCv+ VMCv=VMCv , VM=VMCv=ω∙CVM,
VN=VCv+ VNCv=VNCv , VN =VNCv=ω∙CVN,
VK=VCv+ VKCv=VKCv , VK=VKCv=ω∙CVK.
Из рисунка 2.16 видно, что МЦС лежит в точке пересечения перпендикуляров, проведённых к скоростям точек, при этом всегда справедливо соотношение:
VM/CVM=VN/CVN=VK/CVK=ω
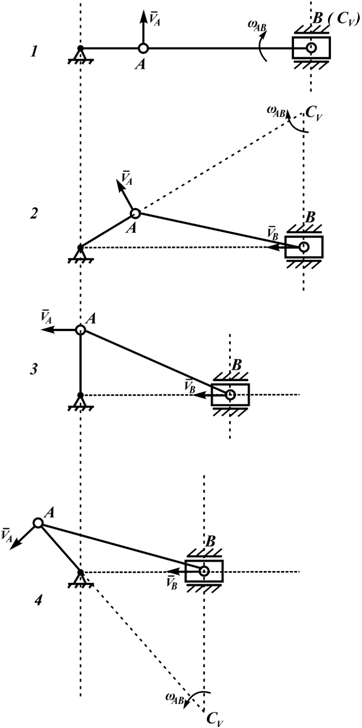
Рисунок 2.17
На рисунке 2.17 показаны примеры определения положения МЦС детали кривошипно-шатунного механизма и приведены формулы для расчета скоростей точек.
- CV совпадает с точкой B, VB=0. Шатун вращается вокруг точки B,
ωAB=VA/ACV=VA/AB; - VA/ACV=VB/BCV=ωAB;
- МЦС лежит в «бесконечности»:
VA/∞=VB/∞=ωAB=0, VB=VA; - VA/ACV=VB/BCV=ωAB.
На рисунках 2.18 — 2.21 приведены примеры определения положения МЦС.
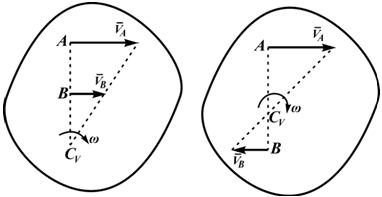
VA/ACV=VB/BCV=ω
Рисунок 2.18
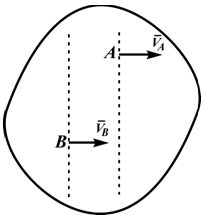
VB||VA
В этом случае МЦС находится в «бесконечности», т.е.
ω=VA/∞=VB/∞=ωAB=0, VB=VA
Рисунок 2.19
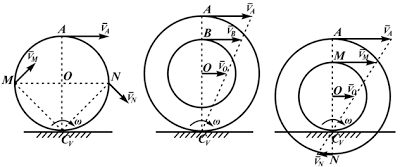
Рисунок 2.20
- VA/2R=V0/R=VM/(R√2)=ω,
- VA/2R=V0/R=VB/(R+r)=ω,
- VA/(R+r)=V0/r=VN/(R-r)=ω
Формулы справедливы при отсутствии проскальзывания в точке CV.
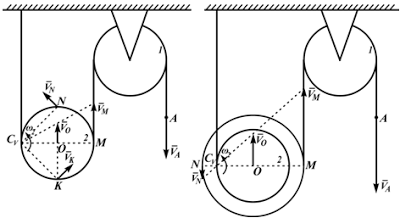
а б
Рисунок 2.21
Для «а»:
VM=VA
VM/MCV=V0/OCV=VN/NCV=VK/KCV=ω2
Для «б»:
VA=VM
VM/MCV=V0/OCV=VN/NCV=ω2
Примеры решения задач >
Ускорение точки в плоскопараллельном движении >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Другой
простой и наглядный метод определения
скоростей точек при плоскопараллельном
движении тела основан на понятии
мгновенного центра скоростей.
Мгновенным
центром скоростей
(МЦС)
называется точка сечения S
тела, скорость которой в данный момент
времени равна нулю.
Легко
убедиться в том, что если тело движется
не поступательно, то такая точка в каждый
момент времени существует и притом
единственная.
П

Рис. 2.32
усть заданы скоростиVA
и VB
двух точек А и В тела. Тогда точка Р,
лежащая на пересечении перпендикуляров
к соответствующим векторам VA
и VB
будет мгновенным центром скоростей,
так как VР
= 0 (рис. 2.32).
Таким
образом, в каждый момент времени
плоскопараллельное движение тела можно
представить как вращательное относительно
оси, проходящей через МЦС. Исходя из
этого, имеем:
VA
= ω·AP;
VA
┴
AP;
VB
= ω·BP;
VB
┴
BP,
где
ω – модуль угловой скорости
![]() тела.
тела.
Отсюда
следует VA/AP
= VB/BP
= ω, т. е. модули скоростей точек тела
пропорциональны их расстояниям до
мгновенного центра скоростей.
Полученные
результаты приводят к следующим выводам:
-
для
определения мгновенного центра скоростей
надо знать только направления скоростей
VA
и VB
каких-нибудь двух точек А и В тела (или
траектории этих точек). МЦС находится
в точке пересечения перпендикуляров,
восстановленных в точках А и В к скоростям
этих точек (или к касательным к
траекториям); -
для
определения скорости любой точки тела
надо знать модуль и направление скорости
какой-нибудь точки А тела и направление
скорости другой его точки В. Тогда,
восстановив из точек А и В перпендикуляры
к VA
и VB,
определим МЦС (точку Р) и по направлению
VA
найдем направление поворота тела. После
того, зная VA,
найдем скорость VВ
любой точки тела. Направлен вектор VВ
перпендикулярно ВР (VВ
┴
ВР) в сторону поворота тела; -
модуль
угловой скорости тела равен отношению
модуля скорости какой-нибудь точки к
её расстоянию до мгновенного центра
скоростей: ω = VA/АР
= VВ/ВР
= VС/СР
= ….
2.20. Различные случаи определения положения мгновенного центра скоростей
Случай
1
П

Рис. 2.33
усть известен вектор
скоростиVA
точки А и линия действия вектора скорости
VВ
точки В (рис. 2.33).
Восстановив
перпендикуляры к скоростям в точках А
и В, определим положение МЦС (точка Р) и
направление вращения тела. Тогда: VA
= ω·АР;
ω = VA/АР;
VВ
= ω·ВР; VС
= ω·СР; VA
┴
АР; VВ
┴
ВР; VС
┴
СР, где ω – модуль угловой скорости
![]() тела.
тела.
В
такой последовательности можно определить
скорость любой точки тела.
На
рис. 2.34 – 2.36 представлены другие случаи
графического определения МЦС.
Порядок
определения МЦС для случаев 2, 3, 4 не
требует особых комментариев. Все формулы,
полученные для первого случая, остаются
справедливыми и для остальных случаев.

Рис. 2.34

Рис. 2.35
Р

Рис. 2.36
ассматривается особый
случай плоскопараллельного движения,
при котором скорости точекVA
и VВ
параллельны (рис. 2.37).

Рис. 2.37
Если
скорости точек А и В параллельны, то
мгновенный центр скоростей находится
в бесконечности (АР =
![]() ;
;
ВР =![]() и т. д.). Очевидно, что в этом случае ω =VA/AP
и т. д.). Очевидно, что в этом случае ω =VA/AP
= VA/![]() = 0. Поэтому скорости точек плоской фигуры
= 0. Поэтому скорости точек плоской фигуры
в рассматриваемый момент времени
геометрически равны:VA
= VB
= VC
=…
Следует
отметить, что при поступательном движении
плоской фигуры скорости всех её точек
в каждый момент времени также геометрически
равны и мгновенный центр скоростей этой
фигуры находится в бесконечности. Если
условие VA
= VB
= VC
= …остается справедливым в течение
некоторого промежутка времени, а не
только в отдельный момент, то движение
плоской фигуры является поступательным.
Если же VA
= VB
= VC
только в некоторый момент времени, то
утверждать, что плоская фигура движется
поступательно, нельзя. В этом случае
говорят, что движение тела является
мгновенно
поступательным.
При мгновенно поступательном движении
происходит смена направлений вращения,
при этом углов

Рис. 2.38
ая скорость![]() = 0, а угловое ускорение
= 0, а угловое ускорение
![]()
≠ 0 (рис. 2.38).
График
зависимости
![]() =f(t)
=f(t)
разбит на две зоны. В зоне I
тело вращается по ходу часовой стрелки,
а в зоне II
– против хода часовой стрелки. При
мгновенно поступательном движении
![]() = 0,
= 0,
![]()
= tg(β)
≠ 0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Мгновенный центр скоростей:
В каждый момент времени при плоском движении фигуры в ее плоскости, если 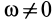 Обозначим ее
Обозначим ее 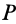
Для доказательства этой теоремы достаточно указать способ нахождения мгновенного центра скоростей, если известны по модулю и направлению скорость какой-либо точки 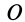 плоской фигуры и угловая скорость этой фигуры в рассматриваемый момент времени. Пусть вращение происходит по часовой стрелке (
плоской фигуры и угловая скорость этой фигуры в рассматриваемый момент времени. Пусть вращение происходит по часовой стрелке (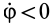 и
и 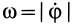 ) (рис. 46). Скорость точки
) (рис. 46). Скорость точки 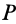 плоской фигуры равна нулю, если скорость полюса
плоской фигуры равна нулю, если скорость полюса 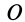 и скорость от вращения вокруг полюса
и скорость от вращения вокруг полюса 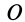 в этой точке равны по модулю, но противоположны по направлению. Эти точки лежат на перпендикуляре к скорости
в этой точке равны по модулю, но противоположны по направлению. Эти точки лежат на перпендикуляре к скорости 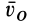 в точке
в точке 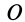 . В других точках векторная сумма двух векторов не может быть равна нулю.
. В других точках векторная сумма двух векторов не может быть равна нулю.
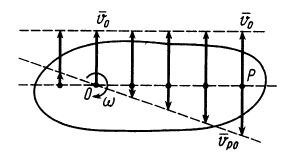
Рис. 46
Итак, если 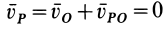 , то
, то 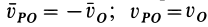 .
.
Ho
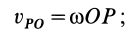
следовательно,
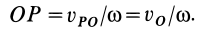
Таким образом, мгновенный центр скоростей находится на перпендикуляре к скорости 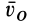 , проведенном из точки
, проведенном из точки 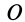 , на расстоянии
, на расстоянии 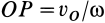 .
.
Мгновенный центр скоростей является единственной точкой плоской фигуры для данного момента времени. В другой момент времени мгновенным центром является уже другая точка плоской фигуры.
Если мгновенный центр известен, то, приняв его за полюс и учитывая, что скорость его в этом случае равна нулю, согласно (3) и (4), для точки 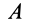 фигуры имеем
фигуры имеем
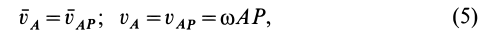
где 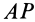 —расстояние от точки
—расстояние от точки 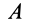 до мгновенного центра скоростей.
до мгновенного центра скоростей.
По направлению скорость 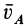 в этом случае перпендикулярна отрезку
в этом случае перпендикулярна отрезку 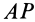 . Для точки
. Для точки 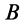 , аналогично,
, аналогично,

причем скорость 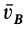 перпендикулярна отрезку
перпендикулярна отрезку 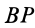 .
.
Из (5) и (6) имеем

и

Следовательно, если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют так же, как и в случае вращения фигуры в рассматриваемый момент вокруг своего мгновенного центра скоростей с угловой скоростью 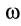 .
.
Для нахождения скоростей точек тела при его плоском движении обычно предварительно находят мгновенный центр скоростей. Но можно применить формулу, выражающую зависимость между скоростями двух точек тела.
Рассмотрим способы нахождения мгновенного центра скоростей. Существует два основных способа его нахождения: из механических условий задачи и по скоростям точек плоской фигуры.
В некоторых случаях удается сразу указать точку плоской фигуры, скорость которой в рассматриваемый момент равна нулю. Эти точки в таких задачах и являются мгновенными центрами скоростей. Так, в случае качения без скольжения одного тела по поверхности другого неподвижного тела точка соприкосновения поверхностей тел и является мгновенным центром скоростей.
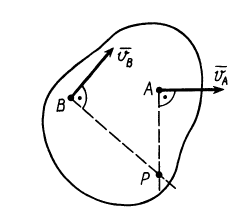
Рис. 47
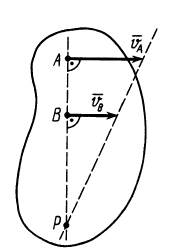
Рис. 48
Например, при качении без скольжения колеса по неподвижной прямой линии (см. рис. 52) и одного колеса по неподвижному другому колесу (см. рис. 61) мгновенный центр скоростей находится в точках соприкосновения колеса с прямой и соответственно колеса с колесом. В общем случае, если известны скорости двух точек плоской фигуры (рис. 47), мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек.
В том случае, когда точки лежат на общем перпендикуляре к скоростям этих точек, скорости точек параллельны и концы их лежат на одной прямой, проведенной через мгновенный центр скоростей (рис. 48 и 49), так как скорости точек пропорциональны расстояниям от этих точек до мгновенного центра скоростей. Если скорости двух точек, расположенных на общем перпендикуляре к этим скоростям, еще и равны (рис. 50), то имеем мгновенное поступательное движение плоской фигуры, при котором скорости всех точек фигуры одинаковы по модулю и направлению. Угловая скорость плоской фигуры при мгновенном поступательном движении равна нулю, и в этом случае, согласно формуле (7), мгновенный центр скоростей находится в бесконечности.
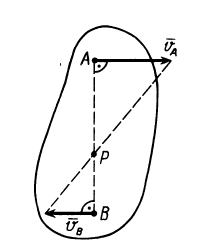
Рис. 49
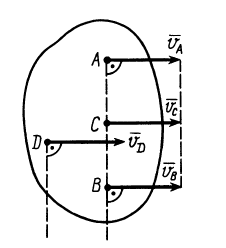
Рис. 50
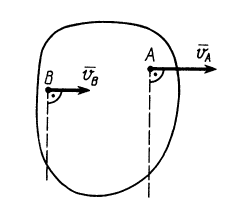
Рис. 51
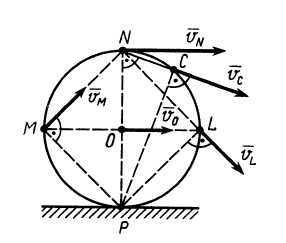
Рис. 52
Заметим, что при мгновенном поступательном движении только скорости точек одинаковы, а их ускорения в общем случае различны. Невозможен случай, когда скорости двух точек, не лежащих на общем перпендикуляре к скоростям, не равны друг другу по модулю, но параллельны (рис. 51), так как для него не выполняется теорема о проекциях скоростей двух точек тела на прямую, соединяющую эти точки.
Пример:
Колесо радиусом 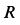 (рис. 52) катится без скольжения по неподвижной прямой, имея скорость центра
(рис. 52) катится без скольжения по неподвижной прямой, имея скорость центра 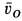 . Определить скорости точек
. Определить скорости точек 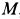 ,
, 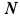 и
и 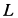 обода колеса в данный момент времени.
обода колеса в данный момент времени.
Решение. Мгновенный центр скоростей в этом случае находится в точке 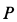 соприкосновения колеса с прямой. Угловая скорость колеса определяется по формуле (7):
соприкосновения колеса с прямой. Угловая скорость колеса определяется по формуле (7):
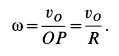
По формуле (5) для скоростей указанных точек имеем
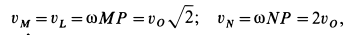
так как
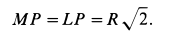
Скорости точек колеса направлены по перпендикулярам к отрезкам прямых, соединяющих мгновенный центр скоростей с рассматриваемыми точками.
Вычисление угловой скорости при плоском движении
Угловую скорость плоской фигуры при плоском движении можно вычислить, согласно ее определению, как
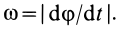
Затем ее можно определить по формуле (7):
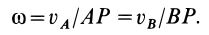
Чтобы определить угловую скорость, надо скорость какой-либо точки плоской фигуры разделить на расстояние от этой точки до мгновенного центра скоростей. Направление вращения определяем по направлению скорости какой-либо точки, считая, что плоская фигура в данный момент вращается вокруг мгновенного центра скоростей с угловой скоростью 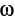 .
.
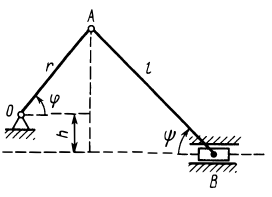
Рис. 53
Угловую скорость при плоском движении можно вычислить путем предварительного нахождения скорости какой-либо точки плоской фигуры от вращения фигуры вокруг другой ее точки, принятой за полюс, например 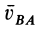 или
или 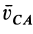 . Тогда угловая скорость, согласно формуле (4),
. Тогда угловая скорость, согласно формуле (4),
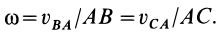
Знак угловой скорости определяют по направлению относительной скорости какой-либо точки фигуры от вращения фигуры вокруг другой ее точки, выбранной за полюс.
Применяют и другие способы определения угловой скорости. Так, если предварительно установить зависимость угла поворота плоской фигуры от линейных и угловых величин других плоских фигур тождественным соотношением, то, дифференцируя его по времени, получаем соотношение, из которого иногда удается определить искомую угловую скорость. Этот способ используют часто для нахождения зависимости угловых скоростей отдельных звеньев плоских механизмов.
Пример:
В кривошипно-шатунном механизме (рис. 53) даны длины кривошипа 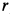 , шатуна
, шатуна 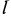 и расстояние
и расстояние 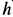 от оси вращения кривошипа до направляющей ползуна
от оси вращения кривошипа до направляющей ползуна 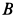 . Установить зависимость между угловыми скоростями кривошипа
. Установить зависимость между угловыми скоростями кривошипа 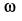 и шатуна
и шатуна 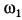 при любом положении механизма.
при любом положении механизма.
Решение. Положение кривошипа 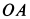 определяется углом
определяется углом 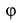 , а шатуна
, а шатуна 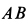 — углом
— углом 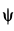 . До тех пор пока
. До тех пор пока 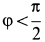 , справедливо тождество
, справедливо тождество
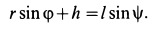
Дифференцируя это тождество по времени, получим
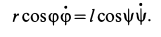
Но 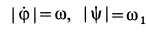 ; следовательно,
; следовательно,
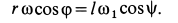
Полученное соотношение и является искомой зависимостью между угловыми скоростями кривошипа и шатуна. При 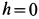 имеем частный случай кривошипно-шатунного механизма. Если дополнительно
имеем частный случай кривошипно-шатунного механизма. Если дополнительно 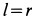 , то
, то 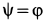 и
и 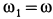 .
.
Направления вращений кривошипа и шатуна противоположны. При вращении кривошипа против часовой стрелки шатун вращается по часовой стрелке.
Ускорения точек тела при плоском движении
Рассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом 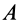 и относительного вращательного вокруг
и относительного вращательного вокруг 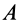 , по теореме о сложении ускорений для точки
, по теореме о сложении ускорений для точки 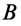 имеем
имеем

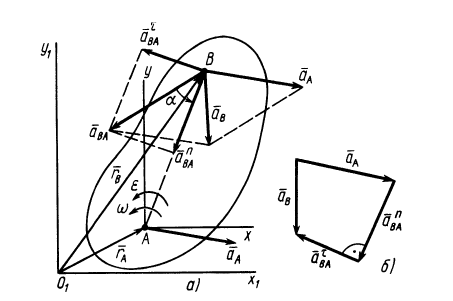
Рис. 54
Так как переносное движение является поступательным вместе с точкой 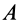 фигуры, то переносное ускорение
фигуры, то переносное ускорение
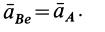
Относительное ускорение 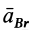 точки
точки 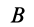 от вращения вокруг полюса
от вращения вокруг полюса 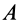 обозначим
обозначим 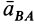 . После этого формула (9) принимает вид
. После этого формула (9) принимает вид

т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг полюса.
Ускорение от относительного вращательного движения вокруг полюса, как и в случае вращения тела вокруг неподвижной оси, состоит из касательной и нормальной составляющих 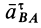 и
и 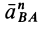 :
:

причем

и _________
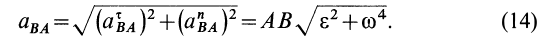
Касательное относительное ускорение 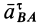 направлено по перпендикуляру к отрезку
направлено по перпендикуляру к отрезку 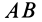 в сторону дуговой стрелки углового ускорения
в сторону дуговой стрелки углового ускорения 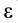 (рис. 54, а). Нормальное относительное ускорение
(рис. 54, а). Нормальное относительное ускорение 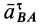 соответственно направлено по линии
соответственно направлено по линии 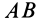 от точки
от точки 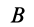 к полюсу
к полюсу 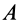 . Наконец, полное относительное ускорение
. Наконец, полное относительное ускорение 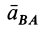 составляет с отрезком
составляет с отрезком 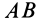 угол
угол 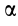 , тангенс которого можно определить по формуле
, тангенс которого можно определить по формуле
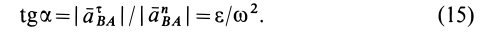
Из формулы (15) следует, что угол 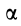 для всех точек плоской фигуры одинаков. При
для всех точек плоской фигуры одинаков. При 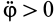 угол
угол 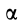 от ускорения
от ускорения 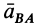 к отрезку
к отрезку 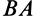 надо откладывать против часовой стрелки. При
надо откладывать против часовой стрелки. При 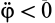 его надо откладывать по часовой стрелке, т. е. во всех случаях, независимо от направления вращения фигуры, угол
его надо откладывать по часовой стрелке, т. е. во всех случаях, независимо от направления вращения фигуры, угол 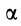 всегда надо откладывать в направлении дуговой стрелки углового ускорения. В соответствии с (10) и (11) можно построить в выбранном масштабе многоугольник ускорений для точки
всегда надо откладывать в направлении дуговой стрелки углового ускорения. В соответствии с (10) и (11) можно построить в выбранном масштабе многоугольник ускорений для точки 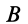 (рис. 54, б).
(рис. 54, б).
Формулу (10), определяющую зависимость ускорений двух точек плоской фигуры, можно получить непосредственным дифференцированием векторного равенства для скоростей, справедливого в любой момент времени. Имеем
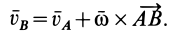
Продифференцируем по времени обе части этого равенства, учитывая изменения векторных величин относительно неподвижной системы координат (полные производные). Получаем
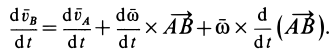
Здесь 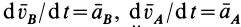 — ускорения точек
— ускорения точек 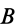 и
и 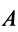 относительно неподвижной системы координат;
относительно неподвижной системы координат; 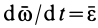 — угловое ускорение плоской фигуры. У вектора
— угловое ускорение плоской фигуры. У вектора 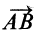 постоянный модуль; следовательно, его производная по времени выражается в форме
постоянный модуль; следовательно, его производная по времени выражается в форме
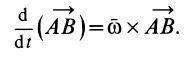
Объединяя полученные результаты, получаем
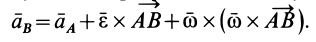
Рассуждения, аналогичные тем, которые проведены для скорости 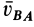 , позволяют сделать вывод о том, что
, позволяют сделать вывод о том, что
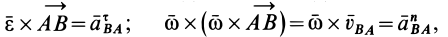
т. е. 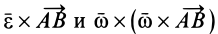 являются соответственно касательным и нормальным ускорениями от вращения плоской фигуры вокруг точки
являются соответственно касательным и нормальным ускорениями от вращения плоской фигуры вокруг точки 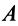 . Следовательно,
. Следовательно,
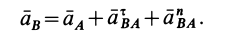
- Заказать решение задач по теоретической механике
Пример:
Колесо радиусом 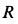 катится со скольжением по неподвижной прямой, совершая плоское движение (рис. 55). Ускорение центра колеса в рассматриваемый момент времени
катится со скольжением по неподвижной прямой, совершая плоское движение (рис. 55). Ускорение центра колеса в рассматриваемый момент времени 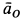 , а угловая скорость и угловое ускорение колеса
, а угловая скорость и угловое ускорение колеса 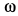 и
и 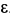 . Дуговые стрелки для
. Дуговые стрелки для 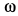 и
и 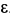 направлены по часовой стрелке, т. е.
направлены по часовой стрелке, т. е. 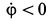 и
и 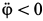 . Определить в этот момент времени ускорения точек
. Определить в этот момент времени ускорения точек 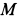 ,
, 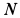 и
и 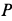 , расположенных на концах вертикального и горизонтального диаметров обода колеса.
, расположенных на концах вертикального и горизонтального диаметров обода колеса.
Решение. Ускорение точки 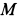 , приняв за полюс точку
, приняв за полюс точку 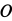 , определим по формуле
, определим по формуле
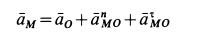
и аналогичным формулам для точек 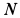 и
и 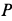 . Для касательного и нормального ускорений точки
. Для касательного и нормального ускорений точки 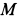 от вращения колеса вокруг точки
от вращения колеса вокруг точки 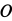 имеем
имеем
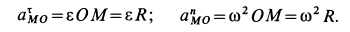
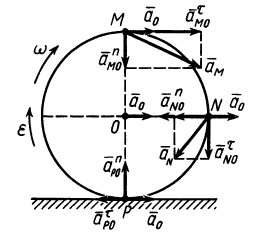
Рис. 55
Ускорение 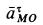 перпендикулярно отрезку
перпендикулярно отрезку 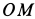 и направлено в сторону, указываемую дуговой стрелкой
и направлено в сторону, указываемую дуговой стрелкой 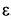 , а ускорение
, а ускорение 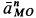 направлено от точки
направлено от точки 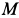 к точке
к точке 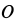 , принятой за полюс. Аналогично направлены ускорения для точек
, принятой за полюс. Аналогично направлены ускорения для точек 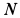 и
и 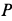 .
.
Так как для точки 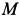 ускорения
ускорения 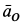 и
и 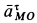 направлены по одной прямой, то, предварительно их сложив, получим две перпендикулярные составляющие ускорения и, следовательно,
направлены по одной прямой, то, предварительно их сложив, получим две перпендикулярные составляющие ускорения и, следовательно,
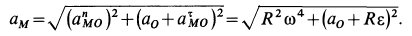
Для точки 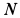
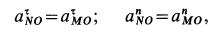
так как
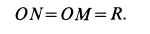
Окончательно для точки 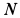 имеем
имеем
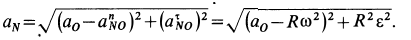
Для точки 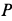 соответственно
соответственно
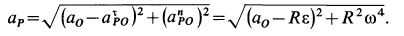
В том случае, когда колесо катится без скольжения, точка 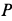 является мгновенным центром скоростей и скорость точки
является мгновенным центром скоростей и скорость точки 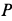 в любой момент времени равна нулю. Скорость точки
в любой момент времени равна нулю. Скорость точки 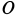 в этом случае можно определить по формуле
в этом случае можно определить по формуле
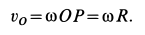
Дифференцируя по времени обе части этого тождества и приравнивая результат дифференцирования, получим
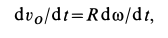
или
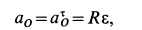
так как точка 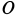 движется прямолинейно, и
движется прямолинейно, и
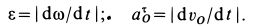
Учитывая, что
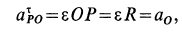
имеем
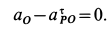
Следовательно, при качении колеса по прямой без скольжения
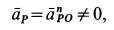
т. е. ускорение мгновенного центра скоростей, скорость которого равна нулю, не равно нулю.
Если угловое ускорение не задано, то при отсутствии скольжения колеса по прямой его можно определить по формуле
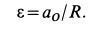
- Мгновенный центр ускорений
- Мгновенный центр вращения
- Вращение твердого тела вокруг неподвижной точки
- Сложное движение точки
- Пространственная система сил
- Центр тяжести
- Кинематика точки
- Плоское движение твердого тела
iSopromat.ru

Рассмотрим формулы и примеры определения положения мгновенного центра скоростей (МЦС) для различных твердых тел и механизмов при плоскопараллельном движении.
Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.
В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю.
Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.

При определении положения МЦС скорость любой точки может быть записана: VM = VCv + VMCv , где точка CV выбрана за полюс. Поскольку это МЦС и VCv=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей:
Из рисунка 2.16 видно, что МЦС лежит в точке пересечения перпендикуляров, проведённых к скоростям точек, при этом всегда справедливо соотношение:

На рисунке 2.17 показаны примеры определения положения МЦС детали кривошипно-шатунного механизма и приведены формулы для расчета скоростей точек.
На рисунках 2.18 — 2.21 приведены примеры определения положения МЦС.


В этом случае МЦС находится в «бесконечности», т.е.

- VA/2R=V0/R=VM/(R√2)=ω,
- VA/2R=V0/R=VB/(R+r)=ω,
- VA/(R+r)=V0/r=VN/(R-r)=ω
Формулы справедливы при отсутствии проскальзывания в точке CV.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Решение задач, контрольных и РГР
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
Набор студента для учёбы

– Рамки A4 для учебных работ
– Миллиметровки разного цвета
– Шрифты чертежные ГОСТ
– Листы в клетку и в линейку
Мгновенный центр скоростей (МЦС)
Зависимость (8.4) позволяет получить простую картину распределения скоростей точек плоской фигуры. Это распределение оказывается точно таким же, как и в случае тела, вращающегося вокруг неподвижной оси. Разница лишь в том, что точка, вокруг которой вращается плоская фигура, со временем изменяет свое положение, т.е. является мгновенным центром вращения.
Мгновенным центром скоростей (или мгновенным центром вращения) называют ту точку плоской фигуры, скорость которой в данный момент времени равна нулю. Покажем, что если угловая скорость фигуры отлична от нуля (со Ф 0), то такая точка существует и единственна.
Пусть в некоторый момент времени известна скорость А точки А фигуры и угловая скорость фигуры со Ф 0.
Проведем прямую AN, перпендикулярную вектору Уд, и отложим на ней (рис. 8.8) отрезок
Найдем скорость точки Р фигуры при помощи векторной формулы (8.4):
Оба вектора в правой части этого равенства перпендикулярны к AN, т.с. параллельны друг другу, и направлены в противоположные стороны (рис. 8.8). Модули их равны, т.к. согласно (8.5)
Поэтому vр = ул + уРд = 0, следовательно, точка Р является мгновенным центром скоростей (МЦС) фигуры. Единственность МЦС следует из процедуры его построения.
Пусть точка Р – мгновенный центр скоростей плоской фигуры, тогда скорость любой точки фигуры выражается в виде
Здесь ВР – это вектор скорости точки В при вращении фигуры вокруг центра Р с угловой скоростью со, вектор в = ВР направлен перпендикулярно отрезку РВ в сторону вращения фигуры (рис. 8.9), а его величина согласно (8.5)
Это значит, что скорость любой точки фигуры находится так, как если бы фигура вращалась в своей плоскости с угловой скоростью со вокруг МЦС (рис. 8.9).
Из равенств vB = со ? ВР и vc = со- СР следует пропорция
т.е. величина скорости точки плоской фигуры пропорциональна её расстоянию от МЦС.
Для решения задач кинематики плоского движения удобно пользоваться следующими правилами построения МЦС.
1. Как видно из рис. 8.9, МЦС – это точка пересечения перпендикуляров к скоростям точек плоской фигуры. Поэтому для построения МЦС достаточно знать направления скоростей двух точек фигуры (при условии, что эти скорости непараллельны).
2. Если скорости двух точек фигуры параллельны, а сами эти точки лежат на общем перпендикуляре к скоростям (рис. 8.10), то положение МЦС можно установить при помощи пропорции (8.9), если известны величины и направления скоростей. Решение пропорции (8.9) можно заменить простым геометрическим построением, показанным на рис. 8.9 штриховой линией: МЦС находится как точка пересечения общего перпендикуляра ВС и линии, соединяющей концы векторов скоростей точек В и С.
3. Если перпендикуляры к скоростям точек параллельны, т.е. не имеют пи одной общей точки (рис. 8.11), то МЦС построить невозможно. Построения (п.8.4) допускают такую ситуацию лишь в том случае, когда угловая скорость фигуры со = 0. Тогда из (8.4) и (8.5) следует, что все точки фигуры имеют одинаковые скорости.
- 4. Если известна скорость А какой-нибудь точки А фигуры и угловая скорость фигуры со, то можно найти МЦС, повторяя построения п. 4.4.
- 5. При качении фигуры по неподвижной кривой без проскальзывания МЦС фигуры находится в точке К её касания с этой кривой (рис. 8.12), так как скорость точки касания фигуры равна нулю.
Продемонстрируем использование МЦС для расчета скоростей.
Пример 2. Стержень АВ длиной 0,6 м совершает плоскопараллельное движение так, что его концы А и В перемещаются вдоль вертикальРешение. Найдем положение МЦС стержня АВ. Для этого построим перпендикуляры к скоростям точек А и В (рис. 8.14). Точка пересечения Р этих перпендикуляров и является МЦС стержня.
ной и горизонтальной направляющих (рис. 8.13). Известно, что точка А движется с постоянной скоростью гд = 2 м/с.
Найти угловую скорость стержня АВ и скорость точки В в тот момент времени, когда угол (р= 30°.
Согласно описанным выше свойствам МЦС (и. 8.4) имеем:
Из первого равенства находим угловую скорость стержня
Из второго равенства определяем величину скорости точки В:
Направления скоростей уд , vв и направление вращения стержня А В согласованы так, как показано на рис. 8.14.
Мгновенный центр скоростей
Мгновенным центром скоростей (МЦС) называется точка в плоскости движения плоской фигуры, скорость которой в данный момент равна нулю.
МЦС является мгновенной неподвижной осью. Поэтому векторы скоростей точек плоской фигуры перпендикулярны отрезкам, соединяющим эти точки с МЦС, и направлены в соответствии с угловой скоростью, а модули скоростей пропорциональны расстояниям точек до МЦС: . Отношение скорости любой точки плоской фигуры к ее расстоянию до МЦС является величиной, равной угловой скорости вращения.
Частные случаи определения МЦС
а) Колесо катится без скольжения. МЦС находится в точке соприкосновения колеса с неподвижной поверхностью:
б) четырехзвенник ОАВО1. Строим МЦС стержня АВ. Перпендикуляры к скоростям точек А и В будут параллельны, т. е. пересекаются в бесконечности. Поэтому МЦС не существует. Стержень АВ совершает мгновенное поступательное движение, и скорости всех точек стержня будут одинаковыми по величине и направлению. В данный момент угловая скорость стержня АВ равна нулю (AB = 0 ).
Сложное движение точки
Сложным движением называют такое движение, при котором точка одновременно участвует в двух или более движениях Абсолютным движением называют движение точки М по отношению к основной системе отсчета O1X1Y1Z1, которую условно принимают за неподвижную. Относительным движением называют движение точки М по отношению к подвижной системе отсчета OXYZ. Переносным движением называют движение подвижной системы отсчета OXYZ относительно основной (неподвижной) системы отсчета O1X1Y1Z1.
Теорема о сложении скоростей
Абсолютной скоростью называют скорость точки М относительно основной системы координат O1X1Y1Z1 и обозначают
Относительной скоростью называют скорость точки М относительно подвижной системы координат OXYZ и обозначают
Переносной скоростью называют скорость той точки подвижной системы координат, с которой в данный момент совпадает движущаяся точка М, и обозначают
Абсолютная скорость точки в сложном движении равна геометрической сумме переносной и относительной скоростей =+
Модуль абсолютной скорости в общем случае находят проектированием выражения на оси координат, так как угол между векторами относительной и переносной скоростей может быть от 0 до 180°:
[spoiler title=”источники:”]
http://studme.org/231821/tehnika/mgnovennyy_tsentr_skorostey
http://studwood.ru/1742015/matematika_himiya_fizika/mgnovennyy_tsentr_skorostey
[/spoiler]

