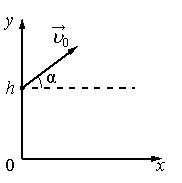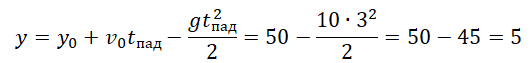Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17980
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
Ответ: 42
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 43.2k
Движение тела, брошенного под углом к горизонту. Полный разбор движения. Вывод формул
Это движение представляет собой совокупность двух видов движения:
- равномерного движения по оси X (горизонтально): скорость v=const, т.к. ускорение a=0
- равнопеременного по оси Y (вертикально): скорость v=v0+at, т.к. ускорение а=-g
Как же найти скорость?
Сначала найдем скорости по X и по Y отдельно.
- Чтобы найти скорость по оси X, которая будет постоянная на всем пути, определим проекцию V0 на ось X:
Проекция V0 на ось Х – это прилежащий к углу α катит:
V0x=V0cosα
Т.к. Vx – постоянна, поэтому:
Vx= V0x=V0cosα
- Чтобы найти скорость по оси Y, которая будет меняться, определим проекцию V0 на ось Y, это будет начальная скорость по вертикальной оси:
Проекция V0 на ось Y – это противолежащий к углу α катит:
V0у=V0sinα
Так как Vy, как мы уже говорили, равнопеременная скорость, то:
Vу= V0у+at
Учитывая, что ускорение направлено против вертикальной оси (а=-g), и подставляя V0y получим:
Vу= V0sinα -gt
Итого:
Зная проекции скорости, можем ли мы восстановить саму скорость? (зная катеты треугольника можем ли мы найти гипотенузу?)
Конечно! Теорема Пифагора.
V2=Vx2+ Vy2
Скорость – дело понятное, как же быть с пройденным путем? Очень просто.
Так как мы сказали, что имеем дело с двумя видами движения в одном, а значит и пути у каждого из видов движения будут разные:
- Горизонтального движение по оси Х равномерное, путь при равномерном движении:
S=V t
Обозначим путь по Х за Х и подставим нашу скорость вместо V, получим:
Х= Vxt= V0cosα t
- Вертикальное движение по оси Y равнопеременное, путь при равнопеременном движении:
Аналогично, обозначим путь по Y за Y, подставим нашу скорость вместо V0 и ускорение а=-g получим:
В итоге:
ВАЖНО! Часто в задачах встречается ситуация, когда нужно найти высоту подъема или дальность полета.
Высота подъема находится очень просто. Все что нужно для решения большинства задач находится в получившихся уравнениях:
- для скорости
- для координат
Верхняя точка отличается тем, что в ней происходит изгиб. Происходит этот изгиб из-за ускорения свободного падения. Полная скорость, т.к. она направлена по касательной, становится направленной горизонтально, а значит проекция полной скорости по Y равна нулю:
Vу= V0sinα –gt=0
Запишем концовку предыдущего уравнения и выразим время — время в этой формуле соответствует той же самой верхней точке, назовем его – время подъема (tп).
V0sinα –g tп =0
Получаем:
Высота подъема – это координата Y, поэтому вставляем tп в уравнение для Y и получаем искомую высоту собственной персоной:
Преобразуем и получим высоту подъема:
Дальность полета – это координата Х в точке падения, поэтому время уже накопится в два раза больше:
Аналогично подставим время в формулу для координаты Х:
Применим формулу из триганометрии: 2sin cos = sin, применим и получим:
Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом к оси ОХ (рис. 1).
Рис. 1. Тело бросили под углом к горизонту
Классическая постановка задач на подобную тематику: тело бросили под углом к горизонту с начальной скоростью
, найти различные параметры движения.
Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2).
Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение)
Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ ( (м/
), а на ось OY (
(м/
).
Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу.
Рис. 3. Тело бросили под углом к горизонту (проекции скоростей)
Для рассмотрения движения тела вдоль осей, введём начальные скорости движения тела вдоль выбранных нами осей (рис. 3). На рисунке представлена часть траектории в самом начале движения. Начальные скорости движения вдоль осей обозначим и
. Исходя из треугольника, катетами которого являются наши проекции (можно построить параллельным переносом), а гипотенузой — модуль вектора начальной скорости (
), можем найти значения необходимых нам проекций:
(1)
(2)
Вернёмся к рисунку 2. Попробуем найти полное время полёта (). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения:
(3)
— т.к. время движения от точки А до B, и от B до C одинаково. Тогда:
(4)
И, учитывая (2):
(5)
Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ().
Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время :
(6)
А с учётом (1) и (5):
=
=
(7)
Перейдём к максимальной высоте полёта (). Данный параметр связан с движением тела вдоль оси OY, которое, как мы выяснили, является равноускоренным/равнозамедленным. Рассмотрим участок BC: для него вдоль соответствующей оси тело без начальной скорости движется с ускорением (
) в течение времени
, формируем уравнение:
(8)
С учётом (5):
=
(9)
Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска.
Рис. 4. Тело бросили под углом к горизонту (конечная скорость)
Далее попробуем найти конечную скорость движения (при таких движениях, конечная скорость — скорость при подлёте к Земле). Рассмотрим конечную точку движения С (рис. 4). Скорость тела направлена под неким углом
. Построим проекции данного вектора на оси OX и OY. На основании построенного треугольника реализуем теорему Пифагора для поиска модуля полной конечной скорости:
(10)
Найдём компоненты вектора . Т.к. движение вдоль оси OX равномерное, значит,
, используя (1):
(11)
Движение вдоль оси OY от точки B в точку C равноускоренное, причём, без начальной скорости за время , тогда:
(12)
Используя (5), получим:
(13)
Подставим (12) и (13) в (10):
=
=
(14)
Для избавления от тригонометрических функций мы воспользовались основным тригонометрическим тождеством. Таким образом, доказано, что конечная скорость такого движения равна начальной, кроме того, из треугольника видно, что тело подлетело к земле под углом .
Вывод:
- для движения тела, брошенного под углом к горизонту, выведены добавочные формулы: (5), (7), (9), которые могут существенно упростить решение задачи.
- представлен один из общих способов нахождения скорости при криволинейном движении (через теорему Пифагора и поиск компонент вектора).
Движение под углом к горизонту, теория и онлайн калькуляторы
Движение под углом к горизонту
Пусть некоторое тело бросили под углом $alpha $к горизонту, с начальной скоростью ${overline{v}}_0$. Введем некоторые допущения: Тело будем рассматривать как материальную точку. Сопротивление воздуха учитывать не будем.
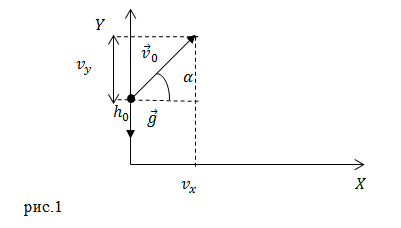
Постанова задачи. Начальные условия движения под углом к горизонту
Тело брошено с высоты ${y=h}_0$; $x_0=0$.
Начальные условия при рассматриваемом движении точки таковы:
[при t=0 cleft{ begin{array}{c}
x_0=0, \
y_0=h, \
v_{0x}=v_0{cos alpha , } \
v_{0y}=v_0{sin alpha . } end{array}
right.(1)]
Вектор ускорения при движении в поле тяжести Земли считают постоянной величиной:
[overline{a}=overline{g}left(2right),]
где $overline{g}$ направлен вертикально вниз и равен по величине приблизительно 9,8 $frac{м}{с^2}.$ Проекция ускорения на ось X равна нулю, а на ось Y равна $a_y=g.$
Уравнение для скорости движения под углом к горизонту
Скорость движения такого тела определяют как:
[overline{v}left(tright)={overline{v}}_0+overline{g}t left(3right),]
где ${overline{v}}_0$ – скорость тела в момент броска. Формулу (2) можно рассматривать как результат сложения скоростей двух независимых движений по прямым линиям, в которых участвует тело, брошенное под углом к горизонту. Это равномерное перемещение с постоянной скоростью ${overline{v}}_0$ в горизонтальном направлении и равноускоренного движения с ускорением $overline{g}$ без начальной скорости в направлении вектора ускорения свободного падения.
Проектируя выражение (3) на оси координат получаем:
[left{ begin{array}{c}
v_x=v_0{cos alpha , } \
v_y=v_0{sin alpha -gt } end{array}
left(4right).right.]
Траектория движения тела
Не смотря на то, что каждое отдельное движение тела происходит по прямой, результирующей траекторией является парабола, лежащая в плоскости в которой находятся векторы ${overline{v}}_0$ и $overline{g}$.
Уравнение перемещения при равнопеременном движении при$overline{a}=overline{g}$:
[overline{s}left(tright)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}(5),]
где ${overline{s}}_0$ – смещение тела в начальный момент времени. В нашем случае $s_0=h$. Уравнения для координат точки, брошенной под углом к горизонту из уравнения для перемещения:
[left{ begin{array}{c}
x=v_0{cos left(alpha right)cdot t, } \
y={h+v}_0{sin left(alpha right)cdot t-frac{gt^2}{2} } end{array}
left(6right).right.]
Из систем уравнений (5) и (6) траектория движения материальной точки получается, задана уравнением:
[y=h+x tg alpha -frac{gx^2}{2v^2_0{cos}^2alpha }left(7right).]
По форме уравнения (7) видно, что траекторией движения является парабола.
Время подъема и полета тела
Время подъема тела при рассматриваемом движении легко определить из системы уравнений (4). В точке максимального подъема вектор скорости точки параллелен оси X, значит $v_y=0$, время подъема ($t_p$) равно:
[t_p=frac{v_0{sin alpha }}{g}left(8right).]
Время, которое тело пребывало в воздухе (время полета($t_{pol}$)) определяют из второго уравнения системы (6), приравнивая координату $y$ к нулю, получают:
[t_{pol}=frac{v_0{sin alpha +sqrt{v^2_0{sin}^2alpha +2gh} }}{g}left(9right).]
Дальность полета и высота подъема
Для того чтобы найти горизонтальную дальность полета тела ($s$) при заданных нами условиях в уравнение координаты $x$ системы уравнений (6) подставим время полета ($t_{pol}$) (9). При $h=0,$ дальность полета равна:
[s=frac{v^2_0{sin left(2alpha right) }}{g}left(10right).]
Максимальную высоту подъема тела ($h_{max}$) находят из второго уравнения системы (6), подставляя в него время подъема ($t_p$) (8):
[h_{max}=h+frac{{v_0}^2{{sin}^2 б }}{2g}left(11right).]
Выражение (11) показывает, что максимальная высота подъема тела прямо пропорциональна квадрату скорости бросания и увеличивается при росте угла бросания.
Примеры задач на движение под углом к горизонту
Пример 1
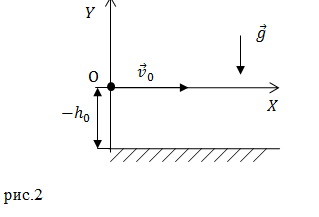
Задание. Маленький шарик лежит на краю горизонтальной поверхности, которая находится на высоте $h$ над уровнем Земли. Ему сообщают начальную скорость направленную горизонтально. По какой траектории будет двигаться шарик? Сопротивление воздуха не учитывайте.
Решение. Начало координат системы отсчета поместим в точку начала падения шарика (рис.2). Основой для решения задачи является уравнение:
[overline{s}left(tright)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(1.1right)]
В проекции на оси координат векторное уравнение даст два скалярных. Так из уравнения (1.1) получаем:
[left{ begin{array}{c}
X: x=v_0t \
Y:y=-frac{gt^2}{2} end{array}
right.left(1.2right).]
Для того чтобы определить какой будет траектория движения шарика нам нужно получить функцию связывающую координаты $y$ и $x$ ($y=y(x)$). Для этого выразим из первого уравнения системы (1.2) время и подставим его во второе уравнение этой же системы:
[t=frac{x}{v_0};;y=-frac{gt^2}{2}=- frac{g}{2}{left(frac{x}{v_0}right)}^2=-frac{g}{2v^2_0}x^2.]
Мы получили функцию:
[y=-frac{g}{2v^2_0}x^2=-kx^2(1.3).]
Уравнение (1.3) – это уравнение параболы. Учитывая, что $t>0$, получим ветвь параболы, вершина в точке бросания.
Ответ. Ветвь параболы.
Пример 2
Задание. Как зависит дальность полета тела, брошенного под углом к горизонту от величины угла бросания? Как влияет сопротивление воздуха на дальность полета тела при его движении под углом к горизонту?
Решение. Будем считать, что тело бросили из начала отсчета ($h=0$). Тогда, дальность полета тела при бросании его под углом к горизонту $alpha $ равна:
[s=frac{v^2_0{sin left(2alpha right) }}{g}left(2.1right).]
Из выражения (2.1) следует, что при заданной скорости бросания дальность полета при увеличении угла$ alpha $растет. Становится максимальной при $alpha =frac{pi }{4}$. Если далее увеличивать угол бросания, то дальность полета тела станет уменьшаться при $alpha =frac{pi }{2}$, тело упадет в точку бросания.
Если учитывать сопротивление воздуха, то дальность полета тела уменьшится в несколько раз.
Читать дальше: движение тела, брошенного под углом к горизонту.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
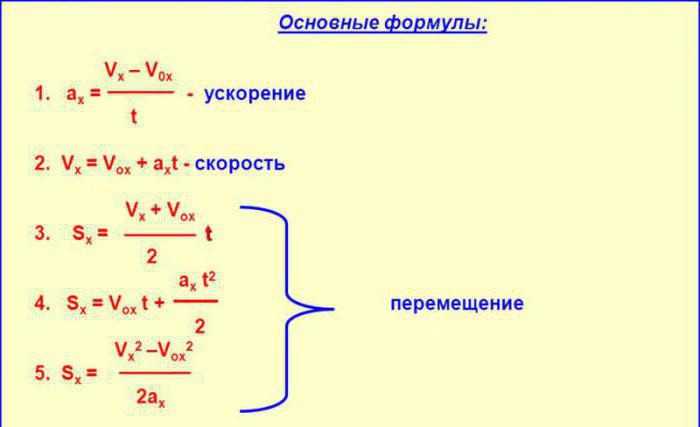
Связываем скорость, ускорение и перемещение
До сих мы достаточно успешно справлялись со всеми предложенными задачами. А что если немножко усложнить их условия? Допустим, что в примере с автомобилем вам известно только ускорение 26,3 метров в секунду в квадрате и конечная скорость 146,3 метров в секунду, а нужно определить пройденное расстояние. Справитесь ли вы с таким заданием? Внимательный читатель уверенно ответит: “Никаких проблем, только дайте мне калькулятор”.
Прежняя задача в новой формулировке кажется более сложной, поскольку в прежних соотношениях всегда присутствовало время. Это значит, что, зная время движения, вы легко сможете решить задачу даже в новой более сложной формулировке. Чтобы определить время движения, достаточно знать ускорение, а также начальную и конечную скорости.
Поскольку:
то получим выражение для времени движения:
Теперь, зная время, можно определить пройденное расстояние по формуле:
Второй член можно исключить, потому что ( v_0 ) = 0. Итак, после подстановки чисел получим:
Поскольку при движении с равномерным ускорением ( s=overline{v}t ), a ( overline{v}={}^1!/!_2(v_1-v_0) ), то получим:
Подставляя в эту формулу выражение для времени движения, получим:
После несложных алгебраических преобразований получим:
Перемещая член ( 2a ) в другую часть уравнения, получим еще одно важное соотношение, которое связывает скорость, ускорение и перемещение:
Уф, это выражение стоит запомнить!
После решения всех этих задач каждый читатель по праву может считать себя повелителем движения.
Подробнее о скорости: что же это такое
Достаточно просто, не так ли? Точнее говоря (физики очень любят точность), скорость равняется изменению положения, деленному на изменение времени. Потому скорость движения вдоль оси X можно выразить следующим образом:
В реальном мире скорость может принимать очень разные формы, некоторые из них описываются в следующих разделах.
Смотрим на спидометр: мгновенная скорость
Итак, у нас уже есть общее представление о скорости. Именно ее измеряет спидометр автомобиля, не так ли? Когда вы катите по прямолинейному шоссе, все, что нужно делать, — всего лишь следить за показаниями спидометра. “Уже 140 километров в час. Пожалуй, сбросим скорость до 120”. Именно так мы часто поступаем в жизни, а иначе говоря, так мы определяем мгновенную скорость.
Движемся постоянно: равномерная скорость
А что если долгое время автомобиль едет со скоростью 120 километров в час? В физике эта скорость называется равномерной (или постоянной), а в жизни она возможна только при движении на абсолютно ровных и прямолинейных дорогах, когда долгое время можно поддерживать движение без изменения скорости.
Равномерное движение с постоянной скоростью является простейшим видом движения, поскольку оно никак не меняется.
Движемся вперед и назад: неравномерное движение
Название этого типа движения говорит само за себя: неравномерное движение означает движение со скоростью, меняющейся со временем. Именно с такой скоростью мы чаще всего сталкиваемся в повседневной жизни. Вот как выглядит уравнение изменения скорости от исходной скорости ( v_1 ) до конечной скорости ( v_0 ):
Остальная часть этой главы посвящена ускорению, которое характеризует неравномерность движения.
Жмем на секундомер и определяем среднюю скорость
Выражение со скоростями не так уж неосязаемо, как может показаться. Измерения скорости можно сделать более конкретными. Допустим, что вам хочется совершить путешествие из Нью-Йорка в Лос-Анджелес, которые находятся на расстоянии около 2781 миль друг от друга. Если предположить, на это путешествие ушло 4 суток, то какой была ваша скорость?
Скорость можно найти, если поделить пройденное расстояние на затраченное на это время:
Итак, результат 695,3 получен, но в каких единицах он выражен?
В этом выражении мили делятся на сутки, т.е. результат равен 695,3 милям в сутки. Это не совсем стандартная единица измерений и вполне естественно было бы поинтересоваться: а сколько это миль в час? Для ответа на этот вопрос нужно перевести сутки в часы, как показано в главе 2. Поскольку в сутках 24 часа, то получим следующий результат:
Итак, получен более понятный результат 28,97 миль в час. Смущает лишь столь малая величина скорости, ведь обычно машины едут со скоростью в 2-3 раза быстрее, однако среднюю скорость для всего путешествия мы вычислили, разделив все расстояния на все время, включая время отдыха.
Средняя скорость и неравномерное движение
Средняя скорость отличается от мгновенной, если только вы не движетесь равномерно, когда скорость вообще не меняется. А средняя скорость неравномерного движения, когда все расстояние делится на все время, может отличаться от мгновенной скорости.
Путешествуя из Нью-Йорка в Лос-Анджелес, вам наверняка придется провести несколько ночей в отелях, и во время вашего отдыха мгновенная скорость автомобиля равна 0 миль в час, а средняя скорость — 28,97 миль в час! Дело в том, что средняя скорость получена в результате деления всего расстояния на все время.
Средняя скорость может зависеть от фактически пройденного пути. Допустим, что, путешествуя по штату Огайо, вы решили подвезти попутчика в штат Индиана и погостить у вашей сестры в штате Мичиган. Все путешествие может иметь вид, показанный на рис. 3.3: первые 80 миль — в штат Индиана, а потом 30 миль — в штат Мичиган.
Если ехать со скоростью 55 миль в час, то для преодоления всего пути длиной 80 + 30 = 110 миль потребуется 2 часа. Но если взять расстояние по прямой между начальной и конечной точкой путешествия, которое равно 85,4 миль, то средняя скорость будет равна:
Таким образом, получена средняя скорость для расстояния от начальной до конечной точки путешествия вдоль пунктирной линии. Но если вам нужно определить скорость для каждого из двух отрезков фактически пройденного пути, то нужно измерить длину каждого из двух отрезков и разделить их на время их прохождения.
При движении с равномерной скоростью это можно сделать легко и просто, поскольку в таком случае средняя скорость равняется мгновенной скорости в любой точке пути.
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
Уравнение скорости при свободном падении:
vy = v0y + gyt
Полезные факты
- В момент падения тела на землю y = 0.
- В момент броска тела от земли y = 0.
- Когда тело падает без начальной скорости (свободно) v = 0.
- Когда тело достигает наибольшей высоты v = 0.
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
План построения чертежа
- Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
- Отмечаются начальная и конечная координаты тела (y и y).
- Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.
Уравнение скорости:
–v = v – gtпад
Уравнение координаты:
Уравнение скорости:
–v = v – gt
Уравнение координаты:
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Чертеж:
Интервал времени между моментами прохождения высоты h:
∆t = t2 – t1
Уравнение координаты для первого прохождения h:
Уравнение координаты для второго прохождения h:
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ. Пример №5
Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Поэтому:
Через 3 с после падения тело окажется на высоте 5 м.
Примеры решения задач
Задание. Движение материальной точки А задано уравнением: $x=2 t^-4 t^$ . Точка начала свое движение при t=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:
Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент времении сравним результат с нулем:
Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.
Ответ. Против оси X.
Формула скорости не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Скорость материальной точки является функцией от времени вида:
где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.
Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:
Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:
Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:
$$ begin10 t-t^=10(2.2) t_=5+sqrt approx 8,8(c) ; t_=5-sqrt approx 1,13(c) end $$
Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:
При решении уравнения (2.3) нам подойдет корень равный:
Ответ. 1) $x=0 mathrm
m>$ 2) $t_=8,8 mathrm, t_=1,13 c, t_=11 c$
Класс: 4
Цели:
- закрепить знания нахождения скорости, времени, расстояния;
- ввести формулы;
- учиться решать задачи с этими величинами по формулам и без них;
- развивать мышление и память;
- прививать любовь к математике.
1. Организация учащихся.
2. Сообщение темы.
— Сегодня на уроке мы закрепим знания нахождения скорости, времени, расстояния. Будем учиться решать задачи с помощью формул.
— А работать мы будем в форме соревнований трех команд:
- 1 ряд — автомобилисты
- 2 ряд — летчики
- 3 ряд — мотоциклисты
— Баллы будем выставлять на доске
3. Соотнести записи с картинкой.
— Как вы думаете, что написано на доске? (Скорости)
— Соотнесите их с нужной картинкой.
(12 км/ч, 60 км/ч, 5 км/ч, 70 км/ч, 120 км/ч, 800 км/ч, 8 км/с, 50 км/ч,250 км/ч.
Автобус, самолет, ракета, пешеход, поезд, велосипедист , автомобиль, пароход, мотоциклист) Каждая команда выставляет по 3 ученика.
— Как вы понимаете км/сек, км/ч, м/мин.
а) В тетрадь записываете ответ с наименованием.
Таблица на интерактивной доске.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.
По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Главное уравнение динамики
Перед тем как давать определение ускорению в физике, приведем главное уравнение динамики, которое носит название второго ньютоновского закона. Его часто записывают в следующем виде:
То есть сила F¯, имеющая внешний характер, оказывала воздействие на некоторое тело в течение времени dt, что привело к изменению количества движения на величину dp¯. Левую часть равенства принято называть импульсом тела. Заметим, что величины F¯ и dp¯ носят векторный характер, и соответствующие им вектора направлены одинаково.
Каждому школьнику известна формула количества движения, она записывается так:
Величина p¯ характеризует запасенную в теле кинетическую энергию (множитель скорости v¯), которая зависит от инерционных свойств тела (множитель массы m).
Если это выражение подставить в формулу 2-го закона Ньютона, то получим следующее равенство:
Введенную величину a¯ называют ускорением.
Передвигаемся и перемещаемся
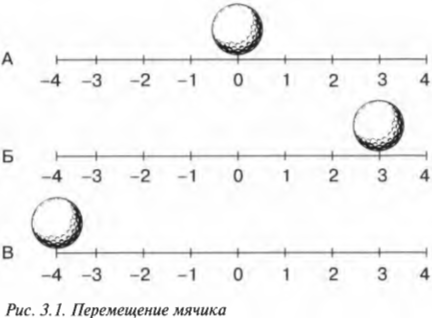
С точки зрения физики перемещение возникает при переходе какого-то объекта из точки 1 в точку 2. Попросту говоря, перемещение — это пройденное объектом расстояние. Рассмотрим, например, движущийся вдоль линейки мячик для игры в гольф, который показан на рис. 3.1. Допустим, что сначала мячик находится возле отметки 0 (схема А).
Пока что все в порядке. Допустим, что мячик сместился на новое место, например на 3 метра вправо (схема Б). В таком случае говорят, что мячик переместился, или произошло перемещение. В данном случае перемещение равно 3 метрам. В исходном положении мячик находился на отметке 0 метров, а в конечном положении — на отметке +3 метра.
В физике перемещение часто обозначают символом ( s ), т.е. в данном случае ( s ) равно 3 метрам.
Ученые любят очень подробно описывать разные ситуации. Например, исходное положение часто обозначают символом( s_0 )(или, в англоязычной литературе,( s_i ) где ( i ) обозначает “initial”, т.е. исходный). А конечное положение часто обозначают символом ( s_1 ) (или, в англоязычной литературе, ( s_f ) где ( f ) обозначает “final”, т.е. конечный). Таким образом, положения на схеме А и схеме Б на рис. 3.1 выражаются символами ( s_0 ) и ( s_1 ) соответственно. А перемещение ( s ) между ними равно их разности, т.е. конечное положение минус исходное положение:
Обратите внимание, что ( s ) отрицательно!
В качестве начальной точки можно выбрать отличное от 0 положение. Например, для перехода между исходным положением на схеме А на рис. 3.1 и конечным положением на схеме В получим следующее перемещение:
Величина перемещения зависит от выбора начальной точки. В простых задачах выбор начальной точки очевиден, а как быть в более сложных случаях, например, когда движение происходит не вдоль линейки?
Разбираемся с осями
В реальном мире объекты редко движутся вдоль линеек, как мячик для гольфа на рис. 3.1. Часто движение происходит в двух или даже трех измерениях пространства. Чтобы измерить движение в двух пространственных измерениях, нужно иметь две пересекающиеся линейки, которые называются осями. Горизонтальную ось называют осью X, а вертикальную — осью Y, а при движении в трехмерном пространстве используют еще одну ось Z (если представить, что оси X и Y лежат в плоскости страницы, то ось Z как бы “торчит” из нее).
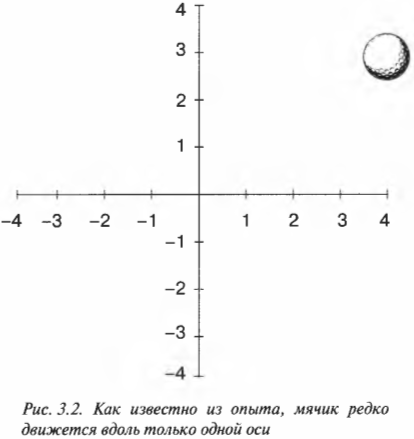
На рис. 3.2 показан пример движения мячика для гольфа в двумерном пространстве. Мячик движется из центра рисунка в верхний правый угол.
Используя оси, можно сказать, что мячик передвинулся на +4 метра по оси X и на +3 метра по оси Y. Новое положение мячика обозначается парой чисел (4; 3), где первое число относится к оси X, а второе — к оси Y, т.е. оно выражается в формате ( (x,y) ).
Чему равно перемещение? Изменение положения по оси X обозначается символом ( Delta x ) (греческий символ ( Delta ) произносится “дельта” и означает “изменение”) и равно: конечное положение минус исходное положение. Если мячик стартует из центра рисунка, т.е. из положения (0; 0), то изменение положения по оси X равно:
Аналогично, изменение положения по оси Y равно:
Допустим, что нужно вычислить величину суммарного перемещения по обеим осям X и Y. Иначе говоря, насколько далеко удалился мячик от исходного положения в центре рисунка? Это можно подсчитать на основе теоремы Пифагора, т.е. выполнить следующие вычисления:
Итак, величина перемещения мячика равна 5 метрам.
Измеряем скорость
В предыдущих разделах рассматривалось движение в одном или двух пространственных измерениях. Однако реальные перемещения происходят за некоторый промежуток времени, т.е. с некоторой скоростью. Например, за какое время произошло перемещение на рис. 3.1 из исходного положения в конечное положение: за 12 лет или 12 секунд?
Остальная часть этой главы посвящена измерению скорости перемещений. Аналогично измерению перемещения в пространстве, можно измерять разницу во времени между началом и концом движения, которая обычно выражается следующим образом:
Здесь ( t_1 ) обозначает конечное время, ( t_0 ) — начальное время, а их разность — количество времени, необходимого для перемещения, например движения мячика от начального к конечному положению. Когда ученые хотят узнать, насколько быстро происходит это событие, то фактически это значит, что они хотят измерить скорость.
Нюансы
На деле же представим, что есть два участка дороги. Один ровный, другой с небольшими бугорками. Скорость у автомобиля пускай будет та же самая, но за счет сопротивления за один и тот же промежуток времени он пройдет на втором участке дороги расстояние меньшее, чем на первом. Однако это уже задача больше из категории динамики, где рассматриваются причины, вызывающие движение тела. Кстати, логично, что при равномерном движении его конечная и начальная скорость совпадают друг с другом, а также с мгновенной скоростью.
При равноускоренном движении все будет несколько иначе. Будет присутствовать положительное ускорение, оно будет постоянным. Но вследствие присутствия ускорения скорость будет ежесекундно изменяться. В связи с этим вопрос о том, как найти скорость в определенный момент времени при наличии ускорения в системе, становится актуальным. Для этого существуют определенные формулы.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют
Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется
Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна
А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.