Как найти скорость поезда 4 класс

Два туриста отправились одновременно навстречу друг другу из пунктов M и N расстояние между которыми 38 км. Через 4 часа расстояние между ними сократилось до 2 км, а ещё через 3 часа первому пешеходу осталось пройти до пункта N на 7 км меньше, чем второму до M. Найдите скорость каждого пешехода. Из двух пунктов A и B, расстояние между которыми равно 160 км, выехали одновременно навстречу друг другу велосипедист и мотоциклист и встретились через 2 часа. Расстояние, пройденное вторым сухогрузом, это сумма расстояний от носа второго сухогруза до кормы первого, длины первого сухогруза, расстояния от его носа первого до кормы второго и длины второго см.

Как Найти Скорость Поезда 4 Класс

Основной формулой при решении задач на встречное движение является всё та же формула, где расстояние выражено через скорость движения и время:

Особенностью применения данной формулы является то, что за скорость принимают скорость сближения двух тел, т.е. сумму их скоростей. Это скорость встречного движения, о которой мы и говорили. Таким образом, формулу для решения задач на встречное движение можно записать так:

1) От двух пристаней, расстояние между которыми 90 км, одновременно вышли навстречу друг другу два теплохода. Первый теплоход шёл со скоростью 20 км/час, второй со скоростью 25 км/час. Через сколько часов они встретились?

2) Две ласточки летят со скоростью 23 м/сек. Через сколько секунд они встретятся, если расстояние между ними 920 м?

3) Два поезда вышли из двух городов одновременно навстречу друг другу. Один поезд шёл со скоростью 63 км/ч. С какой скоростью шёл второй поезд, если расстояние между городами 564 км? Встретились поезда через 4 часа.

4) От двух причалов, расстояние между которыми 90 км, одновременно вышли навстречу друг другу две лодки. Первая шла со скоростью 8 км/час, вторая — со скоростью 10 км/час. Через сколько часов лодки встретились?

5) Из посёлка и города выехали одновременно навстречу друг другу велосипедист и мотоциклист. Велосипедист ехал со скоростью 16 км/час, а мотоциклист со скоростью 54 км/час. Велосипедист проехал до встречи 48 км. Какое расстояние до встречи проехал мотоциклист?

6) Два мальчика одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 200 м. Они встретились через 20 с. Первый бежал со скоростью 5 м/сек. С какой скоростью бежал второй мальчик?

7) С двух станций вышли одновременно два грузовых поезда и встретились через 5 часов. Один поезд проходил в час 29 км, а другой — 35 км. Какое расстояние между этими станциями?

8) Из двух городов одновременно навстречу друг другу выехали 2 автобуса. Скорость первого автобуса 25 км/час, скорость второго — 50 км/час. Первый автобус прошёл до встречи 100 км. Сколько километров прошёл до встречи второй автобус?

9) Расстояние между двумя городами 81 км. Из них одновременно выехали два велосипедиста друг другу навстречу. Один велосипедист проезжает в час на 3 км больше другого. На каком расстоянии от городов они встретились, если встреча произошла через 3 часа после выезда?

10) Два всадника выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 100 км. Всадники встретились через 4 ч. Найдите скорость первого всадника, если скорость второго — 13 км/час.

Учебник Моро 4 класс 2 часть. Страница 6 | matem1234

26) Расстояние по реке между двумя городами 275 км. Из этих городов одновременно навстречу друг другу вышли пароход и баржа. Пароход шёл со скоростью 28 км/час. Найдите скорость баржи, если известно, что её встреча с пароходом произошла через 5 часов после выхода. Скорость км ч Время ч Расстояние км Первый турист Второй турист Условия для составления первого уравнения Уравнение Условия для составления второго уравнения Уравнение Система уравнений Решить задачу с помощью таблицы. Через 4 часа расстояние между ними сократилось до 2 км, а ещё через 3 часа первому пешеходу осталось пройти до пункта N на 7 км меньше, чем второму до M.
В нашем случае люди пробегают 15 км за 1 час, велосипедисты проезжают 25 км за 1 час, а машина за то же время 60 км, то есть движутся с различными скоростями.
1) Каковы скорости движения скворца и мухи?
2) Через сколько секунд после начала движения они встретятся?
3) Какое расстояние они пролетят до места встречи? Из пунктов А и В, расстояние между которыми 480 км, одновременно навстречу друг другу выехали автомобилист и мотоциклист, причем скорость автомобилиста на 10 км ч больше скорости мотоциклиста. Через сколько часов встретятся два пешехода, которые вышли одновременно навстречу друг другу, если скорость одного — 3 км час, а другого — 5 км час.

Как вычислить скорость

По какой формуле определяют скорость тела, если известен его путь и время, за которое он пройден?

Чтобы определить скорость при равномерном движении, нужно путь, пройденный телом за выбранный промежуток времени, разделить на этот промежуток времени:
$Скорость = frac$
или
$upsilon = frac$.

Cкорость тела при равномерном движении – это величина, равная отношению пути ко времени, за которое пройден этот путь.

Соответственно, если автомобиль проезжает в течение 10 с путь, равный 20 метрам (рисунок 2), то его скорость будет равна $frac = 2 frac$ (2 метра в секунду).

Тело	Скорость, $frac$	Тело	Скорость, $frac$
Улитка	0,0014	Пассажирский самолет	220
Черепаха	0,05-0,14	Звук в воздухе при degree C$	332
Муха	5	Пуля автомата Калашникова	760
Пешеход	1,5	Луна вокруг Земли	1000
Конькобежец	13	Молекула водорода при degree C$	1693
Скворец	20	Молекула водорода при $25 degree C$	1770
Страус	22	Земля вокруг Солнца	30 000
Автомобиль	20	Свет и радиоволны	300 000 000

Таблица 1. Средние скорости движения некоторых тел, скорость звука, радиоволн и света

Задачи на движение протяженных тел и сложение скоростей — подготовка к ЕГЭ по Математике

36 секунд, за которые поезд проезжает мимо лесополосы, — это время от момента, когда голова поезда поравнялась с началом лесополосы, до момента, когда хвост поезда поравнялся с концом лесополосы. За это время поезд проезжает расстояние, равное сумме собственной длины и длины лесополосы. Через сколько часов после своего отправления он встретится с пассажирским поездом, если скорость пассажирского поезда равна 90 км ч. 36 секунд, за которые поезд проезжает мимо лесополосы, — это время от момента, когда голова поезда поравнялась с началом лесополосы, до момента, когда хвост поезда поравнялся с концом лесополосы.
Например, чтобы узнать, где будет находиться велосипедист через 1 час после того, как он выехал из дома, нам необходимо знать скорость движения и ее направление.

Существует несколько типов задач на движение. Примеры решения всех типов задач с пояснениями мы рассмотрим в этой статье.

Задачи на движение в одном направлении

Задачи на движении в одном направлении относятся к одному из трех основных видов задач на движение.
Если два объекта выехали из одного пункта одновременно, то, поскольку они имеют разные скорости, объекты удаляются друг от друга. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

Если из одного пункта выехал один объект, а спустя некоторое время в том же направлении вслед за ним выехал другой объект, то они могут как сближаться, так и удаляться друг от друга.
Если скорость объекта, движущегося впереди, меньше движущегося вслед за ним объекта, то второй догоняет первого и они сближаются.
Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

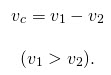
Если скорость объекта, который идет впереди, больше скорости объекта, который движется следом, то второй не сможет  догнать первого и они удаляются друг от друга.
Скорость удаления находим аналогично — из большей скорости вычитаем меньшую:

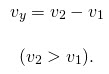
Задачи на скорость сближения

Задача 1

Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение:

Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалится от города на:

40 · 4 = 160 (км)

Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:

60 – 40 = 20 (км/ч) – это скорость сближения автомобилей

Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:

160 : 20 = 8 (ч)

Решение задачи по действиям можно записать так:

1) 40 · 4 = 160 (км) – расстояние между автомобилями

2) 60 – 40 = 20 (км/ч) – скорость сближения автомобилей

3) 160 : 20 = 8 (ч)

Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 2

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

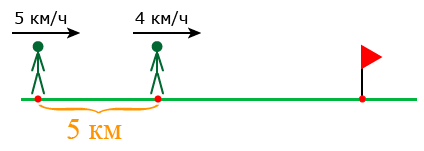
Решение: 

Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:

5 – 4 = 1 (км/ч)

Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:

5 : 1 = 5 (ч)

Решение задачи по действиям можно записать так:

1) 5 – 4 = 1 (км/ч) – это скорость сближения пешеходов

2) 5 : 1 = 5 (ч)

Ответ: Через 5 часов второй пешеход догонит первого.

Задача 3

Из одного села в одном направлении одновременно выехали два велосипедиста. Скорость одного из них — 15 км/ч, скорость другого — 12 км/ч. Какое расстояние будет через ними через 4 часа?

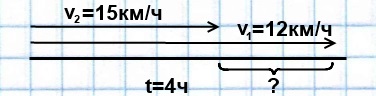
Решение:

1) 15-12=3 (км/ч) скорость удаления велосипедистов

2) 3∙4=12 (км) такое расстояние будет между велосипедистами через 4 часа.

Ответ: Через 4 часа расстояние между велосипедистами составит 12 км.

Задача 4

Из села на станцию одновременно вышел пешеход и выехал велосипедист. Через 2 часа велосипедист опережал пешехода на 12 км. Найти скорость пешехода, если скорость велосипедиста 10 км/ч.

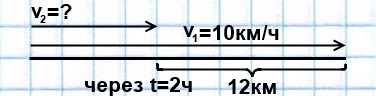
Решение:

1) 12:2=6 (км/ч) скорость удаления велосипедиста и пешехода

2) 10-6=4 (км/ч) скорость пешехода.

Ответ: Скорость пешехода составляет 4 км/ч.

Задачи на скорость удаления

Задача 1

Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.

1. Чему равна скорость удаления между автомобилями?
2. Какое расстояние будет между автомобилями через 3 часа?
3. Через сколько часов расстояние между ними будет 200 км?

Решение:

Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:

80 – 40 = 40 (км/ч)

Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:

40 · 3 = 120 (км)

Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:

200 : 40 = 5 (ч)

Ответ:

1. Скорость удаления между автомобилями равна 40 км/ч.
2. Через 3 часа между автомобилями будет 120 км.
3. Через 5 часов между автомобилями будет расстояние в 200 км.

Движение навстречу друг другу

Если два объекта движутся навстречу друг другу, то они сближаются. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:  

Скорость сближения больше, чем скорость каждого из них.

Задача 1

Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.

Решение:

1) 100 : 25 = 4 (часа ехал один автобус)

2) 50 * 4 = 200

Решение в виде выражения: 50 * (100 : 25) = 200

Ответ: второй автобус проехал до встречи 200 км.

Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?

Решение:

1) 25 + 20 = 45 (сумма скоростей теплоходов)

2) 90 : 45 = 2

Решение в виде выражения:90 : (20 + 25) = 2

Ответ: Теплоходы встретятся через 2 часа.

Задача 3

От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?

Решение:

1) 63 * 4 = 252 (прошел 1 поезд)

2) 564 – 252 =312 (прошел 2 поезд)

3) 312 : 4 = 78

Решение в виде выражения (63 * 4 – 252) : 4 = 78

Ответ: Скорость второго поезда 78 км/час.

Задача 4

Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?

Решение:

1) 12+10=22 (км/ч) скорость сближения велосипедистов

2) 22∙3=66 (км) было между велосипедистами в начале пути.

Ответ: Расстояние между велосипедистами в начале пути было 66 км.

Задача 5

Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого —  60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?

Решение:

1) 60+50=110 (км/ч) скорость сближения поездов

2) 440:110=4 (ч) время, через которое поезда встретятся.

Ответ: Поезда встретятся через 4 часа.

Движение в противоположных направлениях

Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:

Скорость удаления больше скорости любого из них.

Задача 1

Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?

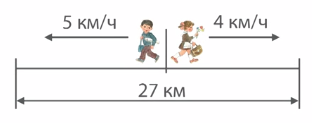
Решение:

Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.

1. 

 (км/ч)

Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.

2. 

 (ч)

Ответ: Через три часа расстояние между переходами будет 27 км.

Задача 2

Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?

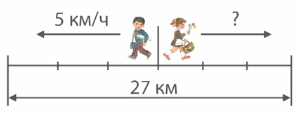
Решение:

Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:

1. 

 (км)

Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.

2. 

 (км)

Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.

3. 

 (км/ч)

Ответ: Скорость второго пешехода – 4 км/ч.

Задача 3

Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?

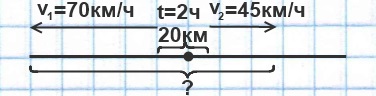
Решение:

1) 70+45=115 (км/ч) скорость удаления поездов

2) 115∙2=230 (км) пройдут поезда вместе за 2 часа

3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.

Ответ: Через 2 часа расстояние между поездами составит 250 км.

Задача 4

Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?

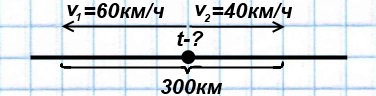
Решение:

1) 60+40=100 (км/ч) скорость удаления мотоциклистов

2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.

Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.

Задачи на скорость, время и расстояние

• Нахождение скорости
• Нахождение времени
• Нахождение расстояния

Скорость — это расстояние, пройденное за единицу времени: за  1  секунду, за  1  минуту, за  1  час и так далее.

Разные объекты имеют разную скорость. Например, средняя скорость пешехода составляет  5  километров в час, скорость велосипедиста —  12  км в час, а автомобиля —  80  км в час. При записи скорости, предлог  в  заменяют наклонной чертой —  км/ч  (например,  15  км/ч).

Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным. Далее будут рассмотрены задачи только на равномерное движение.

Нахождение скорости

Чтобы найти скорость по данному пути (расстоянию) и времени, надо путь разделить на время.

скорость = расстояние : время

Нахождение времени

Чтобы найти время по данному расстоянию и скорости, надо расстояние разделить на скорость.

время = расстояние : скорость

Нахождение расстояния

Чтобы найти расстояние по данным скорости и времени, надо скорость умножить на время.

расстояние = скорость · время

§ 1  Встречное движение

В этом уроке мы познакомимся с задачами на встречное движение.

При решении любой задачи на движение мы сталкиваемся с такими понятиями, как «скорость», «время» и «расстояние».

Скорость – это расстояние, которое преодолевает объект за единицу времени. Измеряется скорость в км/ч, м/сек и т.д. Обозначается латинской буквой ʋ.

Время – это время, за которое объект преодолевает определенное расстояние. Измеряется время в секундах, минутах, часах и т.д. Обозначается латинской буквой t.

Расстояние – это путь, который преодолевает объект за определенное время. Измеряется расстояние в километрах, метрах, дециметрах и т.д. Обозначается латинской буквой S.

В задачах на движение эти понятия взаимосвязаны. Так, чтобы найти скорость, необходимо расстояние разделить на время: ʋ = S : t. Чтобы найти время, надо расстояние разделить на скорость: t = S : ʋ. А чтобы найти расстояние, скорость умножают на время: S = ʋ · t.

Говоря о задачах на встречное движение, используют понятие «скорость сближения». Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени. Обозначается ʋсбл..

Чтобы найти скорость сближения при встречном движении, зная скорости объектов, надо найти сумму этих скоростей: ʋсбл. = ʋ1 + ʋ2. Чтобы найти скорость сближения, зная время и расстояние, необходимо расстояние разделить на время: ʋсбл. = S : t.

§ 2  Решение задач

Рассмотрим взаимосвязь понятий «скорость», «время» и «расстояние» при решении задач на встречное движение.

ЗАДАЧА 1. От двух станций, расстояние между которыми 564 км, одновременно навстречу друг другу вышли два поезда. Скорость одного из них – 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?

Изобразим движение поездов на схеме:

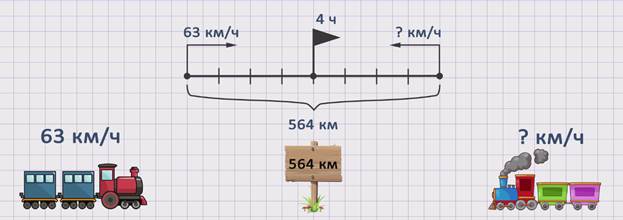
скорость первого поезда обозначим буквой ʋ1 = 63 км/ч. Скорость второго поезда обозначим буквой ʋ2 = ? км/ч. Время в пути обозначим буквой t = 4 ч. Расстояние, которое прошли оба поезда, – буквой S = 564 км.

Поскольку, чтобы найти неизвестную скорость, необходимо знать время, а оно известно и равно 4 часам, и расстояние, прошедшее вторым поездом до встречи, которое не указано в условиях задачи, то необходимо найти это расстояние.. Из условия задачи нам известно все расстояние S = 564 км, скорость первого поезда ʋ1 = 63 км/ч и время t = 4 ч. Зная расстояние, которое прошел до встречи первый поезд, мы сможем узнать и расстояние, которое прошел второй поезд. S1 = ʋ1 · t = 63 · 4 = 252 км. Значит, S2 = S – S1 = 564 – 252 = 312 км. Найдя расстояние, которое прошел до встречи второй поезд, можем найти и скорость второго поезда. ʋ2 = S2 : t = 312 : 4 = 78 км/ч. Получили, что скорость второго поезда равна 78 км/ч.

Рассмотрим второй вариант.

Поскольку, чтобы найти неизвестную скорость, необходимо знать скорость первого поезда, из условий задачи она известна ʋ1 = 63 км/ч, и скорость сближения, которая не оговаривается условиями задачи, то надо найти скорость сближения, используя данные задачи, а именно расстояние S = 564 км и время встречи t = 4 часа. Чтобы найти скорость сближения поездов, можно расстояние разделить на время. ʋсбл. = S : t = 564 : 4 = 141 км/ч. Теперь, зная скорость сближения, можем найти скорость второго поезда. ʋ2 = ʋсбл. – ʋ1 = 141 – 63 = 78 км/ч. Получили, что скорость второго поезда равна 78 км/ч.

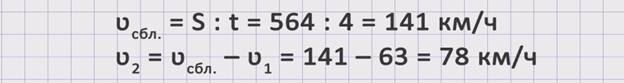
ЗАДАЧА 2. Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится, чтобы встретиться, если скорость первого составляет 20 км/час, а второго – 25 км/час?

Изобразим движение теплоходов на схеме.

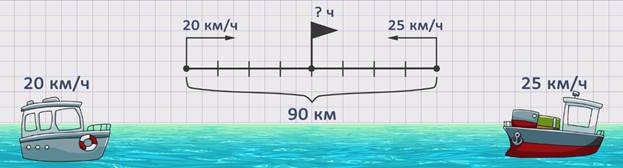
Скорость первого теплохода обозначим буквой ʋ1 = 20 км/ч. Скорость второго теплохода обозначим буквой ʋ2 = 25 км/ч. Расстояние между пристанями обозначим буквой S = 90 км. Время – буквой t = ? часов.

Чтобы ответить на поставленный вопрос задачи, необходимо знать расстояние и скорость сближения, так как t = S : ʋсбл.. Поскольку расстояние нам известно из условия задачи, надо найти скорость сближения. ʋсбл. = ʋ1 + ʋ2 = 20 + 25 = 45 км/ч. Теперь, зная скорость сближения, можем найти неизвестное время. t = S : ʋсбл = 90 : 45 = 2 ч. Получаем, что теплоходам понадобится 2 часа, чтобы встретиться.

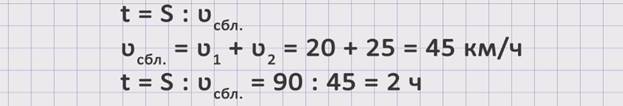
ЗАДАЧА 3. Из поселка и города навстречу друг другу одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость – 50 км/час?

Покажем движение автобусов на схеме.

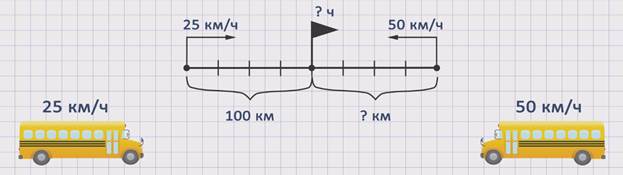
Скорость первого автобуса обозначим буквой ʋ1 = 25 км /ч. Скорость второго автобуса обозначим буквой ʋ2 = 50 км/ч. Расстояние, которое до места встречи проехал первый автобус, обозначим буквой S1 = 100 км. Расстояние, которое проехал до встречи второй автобус – буквой S2 = ? км, а время – буквой t.

Чтобы ответить на вопрос задачи, необходимо знать скорость второго автобуса и время, которое он был в пути до встречи, так как S2 = ʋ2 · t. Поскольку скорость второго автобуса известна из условия задачи, надо найти время. Если мы найдем время, которое был в пути первый автобус, то мы найдем и время, которое был в пути второй автобус, так как они выехали одновременно, а это значит, что до момента встречи автобусы были в пути одинаковое количество времени. Чтобы найти время, можно расстояние, которое проехал первый автобус, разделить на его скорость. t = S1 : ʋ1 = 100 : 25 = 4 часа. Теперь, зная время, можем найти расстояние, которое второй автобус проехал до момента встречи. S2 = ʋ2 · t = 50 · 4 = 200 км. Получили, что второй автобус проехал до встречи 200 км.

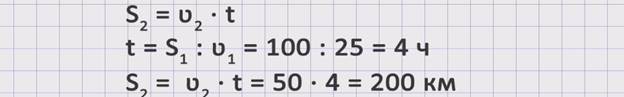
§ 3  Краткие итоги по теме урока

При решение задач на встречное движение следует помнить, что в задачах такого типа выполняются следующие условия:

1.Объекты начинают свое движение одновременно навстречу друг другу, т.е. находятся в пути до встречи одинаковое количество времени; время обозначается латинской буквой t = S : ʋсбл;

2.Расстояние S – это сумма расстояний двух объектов до встречи; S = S1 + S2 или S = ʋсбл· t;

3.Объекты сближаются с определенной скоростью – скоростью сближения, обозначающейся латинской буквой ʋсбл. = S : t или ʋсбл = ʋ1 + ʋ2, соответственно ʋ1 = S1 : t и ʋ2 = S2 : t.

Математика 4 класс. Учебник Моро 2 часть. стр. 11. Странички для любознательных №4. Одновременно навстречу друг другу вышли два поезда: из Москвы – товарный, а из Санкт-Петербурга – пассажирский. Скорость пассажирского поезда была в 2 раза больше, чем скорость товарного. На каком расстоянии от Москвы встретятся поезда, если считать, что расстояние между этими городами 660 км? Как решить задачу? Ну,для взрослого человека и в уме понятно что поезда встретятся на расстоянии 440 километров от Санкт-Петербурга.Но задача в том чтобы объяснить это детям.Для решения нам может понадобиться то,что при движении навстречу друг другу мы складываем скорости транспортных средств. Пусть скорость товарного поезда-х,тогда скорость пассажирского-2х. До встречи они проедут каждый время-t. Скорости складываем: (х+2х)*t=660 xt+2xt=660-это сложили пути. Из первого равенства имеем: 3хt=660 xt=660:3=220-путь товарного поезда 2хt=220*2=440-путь пассажирского поезда Ответ:440 километров на расстоянии от Санкт-Петербурга. система выбрала этот ответ лучшим 88Sky­Walke­r88 [428K] 6 месяцев назад  Эту задачку следует решать так: Мы имеем по условию, что товарный поезд движется со скоростью x, а пассажирский, получается, что со скоростью 2x, то есть в два раза больше. Получается, что все расстояние между Санкт-Петербургом и Москвой можно поделить на три участка. При этом пассажирский поезд прошел два участка, а товарный поезд – один участок. Поделим все рассточние, то есть 660 километров на 3. Получаем 220. Значит, что товарный поезд пройдет 220 км, а пассажирский 440 километров. Санит­арный врач [44.7K] 3 года назад  Странички для любознательных – это такой раздел учебника, где приведены задачи на логику, они считаются чуть более сложными, чем в других разделах учебника. В 4 класс такие задачи на скорость, время и расстояния дети решают еще без уравнений и х. Итак, запишем условия задачи: Дано: S=660 км Vпасс больше Vтоварн в 2 р. Найти: t-? Решение Рассуждаем, два поезда вышли одновременно, раз из Москвы вышел более медленный товарный поезд, то точка встречи двух поездов будет располагаться ближе к Москве. Далее ход мыслей такой, раз скорость товарного поезда меньше в 2 раза, значит за одно и то же время он пройдет расстояние в 2 раза меньше, чем пассажирский. А такие задачи в 4 классе уже решали графическим методом (зная сумму двух отрезков, а один – в 2 раза больше другого): 660:3=220 км – длина меньшего отрезка, это и будет расстояние от места встречи до Москвы. Ответ: 220 км. G1111­1 [92.9K] 6 месяцев назад  Мы читаем эту задачу с позиции своих знаний, и эта задача решается действительно элементарно, взрослыми людьми, которые уже давно знают, что такое поезда, как и с какими скоростями они могут двигаться, а дети только начинают свой путь в мир, и им все это кажется непонятным и необъяснимым. Нам по условию даны два поезда с разными скоростями, и расстояние между городами. Скорый поезд двигается быстрее в два раза, принимаем скорость товарного поезда за единицу и добавляем к ней двойку (скорость скорого поезда) = 3, это значит что условная единица измерения того как поезда двигаются навстречу другу равна 3. Вторым действием узнаем сколько дистанции пути может пройти товарный поезд: 660 (расстояние между городами) / 3 = 220 км, именно столько пройдет товарный поезд до встречи со скорым. Теоретически можно еще узнать сколько прошел скорый поезд: 660 – 220 = 440, второй способ узнать это умножить 220 (коэффициент скорости товарного поезда) * 2 (в столько раз скорый поезд двигается быстрее, взято из условия задачи) = 440 км. прошел скорый поезд до встречи. ну и проверка решения: 220 (километраж грузового поезда) + 440 (километраж скорого поезда) = 660 км. (расстояние между городами) . Ответ: поезда встретятся друг с другом на расстоянии 220 километров от Москвы. Бекки Шарп [71.2K] 3 года назад  Чтобы решать задачи по математике не формально, а понимать почему именно такое решение. лучше представить процесс, описанный в условии. Нам известно, что поезда едут навстречу друг другу с разной скоростью. Если бы они ехали с одинаковой скорость, то встретились бы посередине пути. А теперь представим, какое расстояние преодолевает каждый поезд за один и тот же промежуток времени. Очевидно, что тот, который едет быстрее, проедет более длинный путь. Насколько более длинный если его скорость в 2 раза больше? В 2 раза. То есть, товарный поезд проедет 1 км, а за это время пассажирский проедет 2 км. Заметим, что скорости поездов нам не известны, но они и не нужны. Итак, при сложившейся картинке, становится очевидно, что пассажирский поезд проедет 2 части пути, а товарный одну часть и они встретятся. 660 делим на три и получаем 220 км от Москвы – здесь и встретятся поезда. Extri­mal [148K] 6 месяцев назад  Эта задача предназначена для учеников четвертого класса, поэтому решить ее не составит труда, главное включить логику и вспомнить элементарные правила математики. Пассажирский поезд движется в два раза быстрее, чем товарный, поэтому если мы поделим участок на три части, то пассажирский пройдет два участка пути, а товарный один. Так как общее расстояние составляет 660 километров, делим его на три и понимаем, что один участок составляет 220 километров. Далее мы считаем, что так как пассажирский поезд прошел два участка, то это 440 километров, соответственно товарный прошел один участок, равный 220 километров. Задача решена, получилось все достаточно просто и понятно, даже для школьной программы. СТЭЛС [309K] 6 месяцев назад  У нас уже достаточно вводных по условию задачи, для ее решения. Скорость одного поезда больше другого в два раза. Если предположить что скорость обычно мерим в километрах в час, значит за час один из поездов пройдет расстояние в два раза большее. Расстояние от Москвы делим на три, получаем 220 километров. Почему на три, да потому что один из поездов проедет в два раза больше километров, за то же время. Теперь получается две трети километров пути пройдет один поезд, и одну треть второй. Встреча поездов произойдет ближе к тому населенному пункту, из которого вышел более медленный поезд, а это Москва, а точнее в двухстах двадцати километрах от нее. AlexS­EO [85.9K] более года назад  Решаем так: у нас есть 660 километров пути, которые должны разделиться между двумя поездами (в точке их встречи они проедут ровно 660 километров на двоих). Расходовать километраж они будут так: товарный – х, а пассажирский – 2х; 660 – х – 2х = 0, 3х = 660, х = 660 / 3, х = 220. В точке, удаленной от начала пути товарного поезда на 220 километров и от начала пути пассажирского поезда на 440 километров, эти поезда должны встретиться. Maste­r-Marga­rita [135K] 3 года назад  Мне в детстве было легче решать такие задачи, когда я оставляла лишь один вид транспорта. Условие что скорость пассажирского поезда в 2 раза больше товарного, я заменяла представлением, что часть пути поезд шел со скоростью в 2 раза больше обычной, а потом с обычной. Тогда надо лишь определить на каком расстоянии от города он снизил скорость. 1)660:3 = 220 2)2*220 = 440 Все. Задача решена в два действия. bezde­lnik 1 [1.1K] 3 года назад  Товарный поезд пройдёт до встречи некоторую часть пути,а пассажирский поезд пройдёт до встречи в 2 раза большей путь. Всего они пройдут 3 части пути. Одна часть пути равна 660/3=220 км. Значит товарный поезд пройдёт до встречи 220 км, а скорый 220*2=440 км/ч или 660-220=440 км/ч. Знаете ответ?

Смотрите также: Математика 4 класс. Как решить задачу про овощи, рейсы и машины? ВПР по математике 4 класс 2020, задания, ответы, демоверсии, где найти? Математика 4 класс. Как решить задачу про солдатиков и машинки? Волкова, Математика 4 класс. Рабочая тетрадь №1. Какие ответы на стр. 18? Волкова, Математика 4 класс. Рабочая тетрадь №1. Какие ответы на стр. 17? Волкова, Математика 4 класс. Рабочая тетрадь №1. Какие ответы на стр. 16? Волкова, Математика 4 класс. Рабочая тетрадь №1. Какие ответы на стр. 15? Волкова, Математика 4 класс. Рабочая тетрадь №1. Какие ответы на стр. 14? Волкова, Математика 4 класс. Рабочая тетрадь №1. Какие ответы на стр. 13? Волкова, Математика 4 класс. Рабочая тетрадь №1. Какие ответы на стр. 12?