поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,944 -
разное
16,904
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
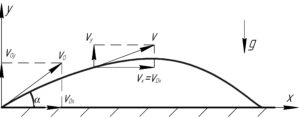
С башни высотой h = 25 м бросили камень со скоростью v0
= 15 м/с под углом α = 300 к горизонту. Определите: время полета камня; дальность
полета камня в горизонтальном направлении; скорость полета камня в момент
падения на землю; угол β,
который составит траектория движения камня с горизонтом в точке его падения на
землю. Сопротивление воздуха не учитывать.
Решение.
Сделав чертеж,
выберем систему координат так, чтобы ее начало совпадало с точкой бросания, а
оси были направлены следующим образом: OX – вдоль
поверхности
земли; OY – по нормали в ней в сторону
начального смещения камня. Сложное движения камня по параболе в данном случае
можно представить как результат сложения двух прямолинейных движений:
прямолинейного движения вдоль оси OX и движения тела,
брошенного вертикально вниз, вдоль оси OY.
Составим систему уравнения скорости и
перемещения для их проекций по каждому направлению:
vx = v0 cos α, x = v0 cos α•t;
vy = v0 sin α – gt, y = v0 sin α•t – gt.
В момент времени t, когда камень упадет на землю, его координаты x = s, y = –h. Тогда для определения t получаем уравнение
–h = v0 sin α•t – (gt•t)/2.
Откуда находим время

Дальность полета камня s определим из уравнения

Скорость камня в момент падения на
землю можно выразить формулой

где
.
Подставим вместо vx и vy их выражения, получим скорость полета камня в момент падения на землю

Ответ: t = 3,2 c, s = 41 м, v = 27 м/с.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Условие задачи:
Камень, брошенный с земли под углом 45° к горизонту, через 0,8 с после начала движения имел вертикальную составляющую скорости 12 м/с. Чему равно расстояние между точкой бросания и местом падения камня?
Задача №1.6.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(alpha=45^circ), (t_1=0,8) с, (v_y=12) м/с, (L-?)
Решение задачи:
Поскольку нужно определить дальность полета, то запишем уравнения движения камня в проекциях на введенные нами оси, а далее уже определим, каких данных нам не хватает. Уравнения, как всегда, выглядят стандартно, поскольку в задаче нет ничего необычного.
[left{ begin{gathered}
ox:x = {v_0}cos alpha cdot t,,,,,,,,,,,,,,,,(1) hfill \
oy:y = {v_0}sin alpha cdot t – frac{{g{t^2}}}{2},,(2) hfill \
end{gathered} right.]
Когда камень ударится о землю, его ордината (y) будет равна нулю, поэтому приравняем уравнение (2) к нулю и найдем корни получившегося уравнения.
[y = 0 Rightarrow {v_0}sin alpha cdot t – frac{{g{t^2}}}{2} = 0]
[tleft( {{v_0}sin alpha – frac{{gt}}{2}} right) = 0]
[left[ begin{gathered}
t = 0 hfill \
t = frac{{2{v_0}sin alpha }}{g} hfill \
end{gathered} right.]
Первый корень не удовлетворяет условию падения камня, поскольку он не мог взлететь и удариться о землю в ту же секунду.
Тогда второй корень подставим в уравнение (1) и получим формулу для определения дальности полета.
[L = frac{{2{v_0}cos alpha cdot {v_0}sin alpha }}{g} = frac{{v_0^2sin 2alpha }}{g}]
Отлично, значит нам необходимо узнать начальную скорость камня (в момент броска), и после мы сможем сосчитать ответ. Для этого запишем уравнение скорости для вертикальной ее составляющей.
[{v_y} = {v_{0y}} – gt_1 = {v_0}sin alpha – gt_1]
Из него выразим начальную скорость камня и подставим ее в формулу дальности полета.
[{v_0} = frac{{{v_y} + gt_1}}{{sin alpha }}]
В итоге получена формула в общем виде:
[L = {left( {frac{{{v_y} + gt_1}}{{sin alpha }}} right)^2}frac{{sin 2alpha }}{g}]
Как всегда, подставим все известные величины в СИ и подсчитаем ответ:
[L = {left( {frac{{12 + 10 cdot 0,8}}{{sin 45^circ }}} right)^2}frac{{sin 90^circ }}{{10}} = 80; м]
Ответ: 80 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.6.2 Баскетболист бросает мяч в кольцо. Скорость мяча после броска
1.6.4 Минимальная скорость при движении тела, брошенного под углом
1.6.5 На некоторой высоте одновременно из одной точки брошены
Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле v=sqrt{2gh}. Найдите скорость (в м/с),с которой ударится о землю камень, падающий с высоты 90 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
h = 90 м
g = 9,8 м/с2
v – ?
Подставим все значения в формулу и найдём v:
v=sqrt{2gh}=sqrt{2·9,8·90}=sqrt{1764} = 42
Ответ: 42.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.8 / 5. Количество оценок: 15
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
2017-05-21
Камень, брошенный с высоты $h = 2,1 м$ под углом $alpha = 45^{ circ}$ к горизонту, падает на землю на расстоянии $s = 42 м$ (по горизонтали) от места бросания (рис.). Найти начальную скорость камня, время полета и максимальную высоту подъема над уровнем земли. Определить также радиусы кривизны траектории в верхней точке и в точке падения камня на землю.
Решение:
Из условия задачи известно направление вектора начальной скорости $v_{0}$ камня, который можно рассматривать как материальную точку.
Если пренебречь сопротивлением воздуха, то $vec{a} = vec{g}$, т. е. ускорение постоянно, направлено по вертикали вниз и равно $9,8 м/с^{2}$.
Векторы начальной скорости и ускорения образуют некоторый угол, не равный ни 0, ни $pi$, поэтому движение криволинейное. Поскольку $a = const$, движение плоское и для описания его достаточно двух осей координат, что позволит сложное криволинейное движение камня рассматривать как совокупность двух прямолинейных движений. Если ось ОХ направить по горизонтали, а ось ОY — по вертикали, то движение вдоль оси ОХ равномерное, так как проекция ускорения $a_{x} = 0$, а движение вдоль оси ОY — равнопеременное ($a_{y} = – g$). Для нахождения закона движения необходимо знать, как было указано ранее, начальные условия, т. е. координаты и скорость в начальный момент времени. Числовое значение начальной скорости неизвестно, однако закон движения, включающий неизвестную начальную скорость, может быть записан. Координаты точки падения можно найти из условия. Подставив их в закон движения, получим систему уравнений, содержащую в качестве неизвестных начальную скорость и время полета.
Максимальную высоту найдем из условия, что в верхней точке траектории вертикальная составляющая скорости обращается в нуль.
Зная законы изменения проекций $v_{x}$ и $v_{y}$ со временем, можно найти модуль и направление скорости для любого момента времени. Вектор ускорения постоянен и известен ($vec{a} = vec{g}$), следовательно, для любого момента времени можно определить нормальное ускорение (проекцию вектора а на ось п, перпендикулярную вектору скорости и направленную к центру кривизны траектории) и радиус кривизны траектории.
Начало отсчета удобно выбрать в точке бросания ($x_{0} = y_{0} = 0$). В системе координат XOY (см. рис.)
$a_{x} = 0, v_{x} = const = v_{0} cos alpha, x = v_{0} cos alpha cdot t$; (1)
$a_{y} = – g, v_{y} = v_{0} sin alpha – gt, y = v_{0} sin alpha cdot t – gt^{2}/2$. (2)
Закон движения записан, хотя значение $v_{0}$ неизвестно. При $t = tau$ в конечной точке траектории $x = s; y = – h$. Тогда уравнения (1) и (2) примут вид
$s = v_{0} cos alpha cdot tau, – h = v_{0} sin alpha cdot tau – g tau^{2}/2$.
Данные уравнения составляют систему с двумя неизвестными $v_{0}$ и $tau$. Решение этой системы:
$tau = sqrt{2(h + s tg alpha)/g} = 3 с; v_{0} = s/( tau cos alpha) = 20 м/с$.
Найдем максимальную высоту подъема камня над землей:
$H = h + y_{M}$.
При $y = y_{M}$ имеем $v_{y} = 0, t = t_{1}$. Подставив в уравнения (2) $v_{y} = 0$, найдем время подъема $t_{1} = (v_{0}/g) sin alpha$. Тогда
$y_{max} = v_{0}^{2} sin^{2} alpha/(2g), H = h + v_{0}^{2} sin^{2} alpha / (2g) = 12 м$.
В верхней точке траектории $v_{y} = 0$, поэтому $v_{M} = v_{x}$. Следовательно, $vec{a} perp vec{v}_{M}$. Это значит, что $a_{n} = a = g$. Зная нормальное ускорение и скорость, найдем радиус кривизны траектории в точке М:
$r_{M} = v_{M}^{2}/a_{n} = (v_{0}^{2} / g) cos^{2} alpha = 20 м$.
В точке В (рис.) скорость
$v_{B} = sqrt{v_{x}^{2} + v_{y}^{2}} = sqrt{v_{0}^{2} cos^{2} alpha + (v_{0} sin alpha – g tau)^{2}} = 20,8 м/с$. (3)
Нормальное ускорение
$a_{n} = v_{B}^{2} / r_{B} = g sin beta$.
Здесь $sin beta = v_{x}/v_{B} = v_{0} cos alpha / v_{B}$, где $beta$ — угол между векторами ускорения и скорости. Тогда радиус кривизны траектории в точке В
$r_{B} = v_{B}^{2} /(gv_{0} cos alpha ) = 67 м$.



