Закон сохранения механической энергии и закон сохранения импульса при упругом ударе способствует нахождению решения механических задач с неизвестными действующими силами, то есть задания с ударным взаимодействием тел.
Применение такого вида задач используется в технике и физике элементарных частиц.
Удар или столкновение – это кратковременное взаимодействие тел с последующим изменением их скорости.
При столкновении действуют неизвестные кратковременные ударные силы. Закон Ньютона не разрешит ударное взаимодействие, а позволит только исключить сам процесс столкновения и получить связь между скоростями тел до и после столкновений без промежуточных значений.
Механика применяет такое определения абсолютно упругих и абсолютно неупругих ударов.
Абсолютно неупругий удар. Скорость
Абсолютно неупругий удар – это ударное взаимодействие с соединением (слипанием) движущихся тел.
Сохранение механической энергии отсутствует, так как переходит во внутреннюю, то есть нагревание.
Попадание пули в баллистический маятник – характерный пример действия энергии абсолютно неупругого удара, где
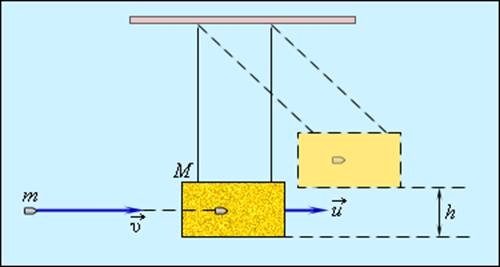
М – подвешенный ящик с песком, показанный на рисунке 1.21.1, m – горизонтально летящая пуля с v→ скоростью движения, застревающая в ящике. Определение скорости пули возможно по отклонению маятника.
Если скорость ящика с пулей обозначить как u→, тогда, используя формулу сохранения импульса, получаем:
mv=(M+m)u; u=mM+mv.
Когда пуля застревает в песке, то механическая энергия теряется:
∆E=mv22-(M+m)u22=MM+m·mv22.
M (M + m) обозначает долю кинетической энергии выпущенной пули и прошедшей во внутреннюю энергию системы. Тогда
∆EE0=MM+m=11+mM.
Использование формулы подходит для задач с наличием баллистического маятника и другого неупругого соударения разномасных тел.
Когда m << М ∆EE0→12, тогда происходит переход кинетической энергии во внутреннюю. Когда m = M ∆EE0→0, только половина кинетической переходит во внутреннюю. Если имеется неупругое соударение движущегося тела большей массой с неподвижным, имеющим (m>>М), отношение принимает вид ∆EE0→0.
Расчет движения маятника производится по закону сохранения механической энергии. Получаем
(M+m)u22=(M+m)gh; u2=2gh.
В данном случае h является максимальной высотой подъема маятника. Отсюда следует, что
v=M+mm2gh.
При известной высоте h возможно определение скорости пули v.
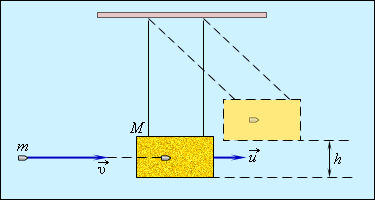
Рисунок 1.21.1. Баллистический маятник.
Абсолютно упругий удар
Абсолютный упругий удар – это столкновение с сохранением механической энергии системы тел.
Большинство случаев столкновения атомов подчинено законам абсолютного упругого центрального удара. Закон сохранения импульса и механической энергии сохраняются при таком ударе. Для примера используется столкновение при помощи центрального удара бильярдных шаров. Один из них находится в состоянии покоя, как изображено подробно на рисунке 1.21.2.
Центральный удар – это соударение, когда скорости шаров направлены по линии центра.
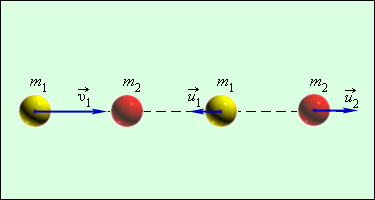
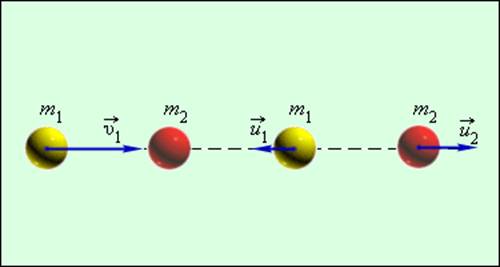
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров.
Встречаются случаи, когда массы m1 и m2 не равны. Тогда, используя закон сохранения механической энергии, получаем
m1v122=m1v122+m2v222.
За v1 принимается скорость при абсолютном упругом ударе первого шара перед столкновением, а v2=0 скорость второго шара, u1 и u2 – скорости после столкновения.
Запись закона сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, принимает вид:
m1v1=m1u1+m2u2.
Полученная система из двух уравнений позволяет найти неизвестные скорости u1 и u2 шаров после столкновения.
u1=m1-m2v1m1+m2; u2=2m1v1m1+m2.
Если массы равны, то есть, тогда происходит остановка первого шара (u1=0), а второй продолжает движение u2=v1. происходит обмен скоростями и импульсами.
При наличии нулевой скорости второго шара (v2≠0), задача могла бы свестись к предыдущей с переходим в новую систему отсчета с равномерным и прямолинейным движением и скоростью v2 относительно «неподвижной» системы. В такой системе второй шар покоится до удара, а первый имеет скорость v1’=v1–v2. После определения скорости шаров v1 и v2 производится переход к «неподвижной» системе.
С помощью закона сохранения механической энергии и импульса, можно определить скорости шаров после столкновений только с известными скоростями до соударения.
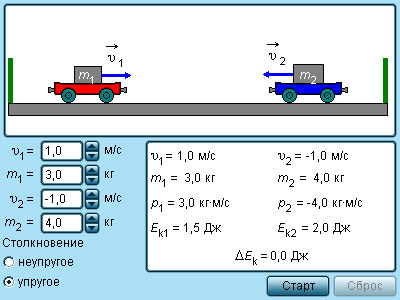
Рисунок 1.21.3. Модель упругие и неупругие соударения.
При столкновении атомов или молекул применяется понятие центрального или лобового удара, который редко применим на практике. Нецентральный упругий удар не направлен по одной прямой.
Частный случай нецентрального упругого удара – соударение бильярдных шаров с одинаковой массой при обездвиженном одним из них, а другим направленным не по линии центра. Данная ситуация приведена на рисунке 1.21.4.
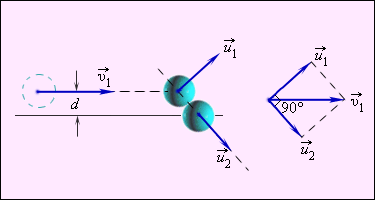
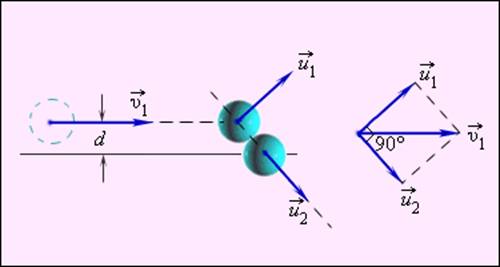
Рисунок 1.21.4. Нецентральное упругое соударение шаров с одинаковой массой, где d является прицельным расстоянием.
Нецентральное ударение характеризуется тем, что разлетатание шаров происходит под углом относительно друг друга. Чтобы определить скорости v1 и v2 после соударения, необходимо знать нахождение положения линии центров в момент удара или предельное расстояние d, изображенное на рисунке 1.21.4.
Предельное расстояние
Предельным расстоянием называют расстояние между двумя линиями, которые проведены через центры шаров параллельно относительно вектора скорости v1→ летящего шара.
При одинаковых массах шаров векторы v1→ и v2→ имеют перпендикулярное направление друг к другу. Это возможно показать с помощью применения законов сохранения импульса и энергии. Если m1=m2=m, тогда определение примет вид
v1→=u1→+u2→; v12=u12+u22.
Первое равенство значит, что векторы v1→, u1→, u2→ образуют треугольник, называемый диаграммой импульсов, второе – для его разрешения применяют теорему Пифагора. Угол, располагаемый между u1→ и u2→, равняется 90 градусов.
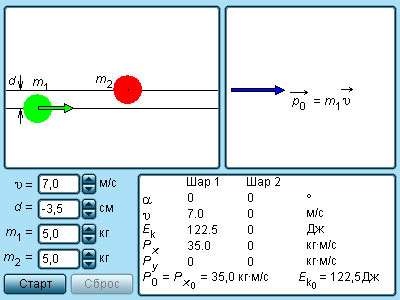
Рисунок 1.21.5. Модель соударения упругих шаров
Примером применения
законов сохранения импульса и энергии
при решении реальной физической
задачи является удар абсолютно упругих
и неупругих тел.
Удар
(или соударение)
—
это столкновение двух или более тел,
при котором взаимодействие длится очень
короткое время. Исходя из данного
определения, кроме явлений, которые
можно отнести к ударам в прямом смысле
этого слова
28
(столкновения
атомов или биллиардных шаров), сюда
можно отнести и такие, как удар человека
о землю при прыжке с трамвая и т. д. При
ударе в телах возникают столь
значительные внутренние силы, что
внешними силами, действующими на
них, можно пренебречь. Это позволяет
рассматривать соударяющиеся тела
как замкнутую систему и применять к ней
законы сохранения.
Тела
во время удара претерпевают деформацию.
Сущность удара заключается в том,
что кинетическая энергия относительного
движения соударяющихся тел на короткое
время преобразуется в энергию упругой
деформации. Во время удара имеет
место перераспределение энергии между
соударяющимися телами. Наблюдения
показывают, что относительная скорость
тел после удара не достигает своего
прежнего значения. Это объясняется
тем, что нет идеально упругих тел и
идеально гладких поверхностей.
Отношение нормальных составляющих
относительной скорости тел после и до
удара называется коэффициентом
восстановления :
=
v’n/vn.
Если
для сталкивающихся тел =0,
то такие тела называются абсолютно
неупругими, если
=1—абсолютно
упругими.
На
практике для всех тел 0<<1
(например, для стальных шаров 0,56,
для шаров из слоновой кости 0,89,
для свинца 0).
Однако в некоторых случаях тела можно
с большой точностью рассматривать либо
как абсолютно упругие, либо как
абсолютно неупругие.
Прямая,
проходящая через точку соприкосновения
тел и нормальная к поверхности их
соприкосновения, называется линией
удара. Удар
называется центральным,
если
тела до удара движутся вдоль прямой,
проходящей через их центры масс. Мы
будем рассматривать только центральные
абсолютно упругие и абсолютно
неупругие удары.
Абсолютно
упругий удар — столкновение
двух тел, в результате которого в обоих
взаимодействующих телах не остается
никаких деформаций и вся кинетическая
энергия, которой обладали тела до удара,
после удара снова превращается в
кинетическую энергию

.
Для абсолютно
упругого удара выполняются закон
сохранения импульса и закон сохранения
кинетической энергии.
Обозначим
скорости шаров массами m1
и
m2
до удара через v1
и
v2,
после
удара — через v’1
и
v’2
(рис.
18). При прямом центральном ударе
векторы скоростей шаров до и после удара
лежат на прямой линии, соединяющей их
центры. Проекции векторов скорости на
эту линию равны модулям скоростей. Их
направления учтем знаками: положительное
значение припишем движению вправо,
отрицательное — движению влево.
При указанных
допущениях законы сохранения имеют вид

Произведя
соответствующие преобразования в
выражениях (15.1) и (15.2), получим
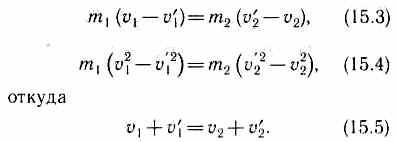
Решая уравнения
(15.3) и (15.5), находим

Разберем несколько
примеров.
29

Проанализируем
выражения (15.8) и (15.9) для двух шаров
различных масс:
а) m1
=m2.
Если
второй шар до удара висел неподвижно
(v2=0)
(рис.
19), то после удара остановится первый
шар (v’1=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(v’2
= v1);
б)
m1>m2.

Первый
шар продолжает двигаться в том же
направлении, как и до удара, но с меньшей
скоростью (v’1<v1).
Скорость
второго шара после удара больше, чем
скорость первого после удара (v’2>v’1)
(рис.20);

в)
m1<m2.
Направление
движения первого шара при ударе изменяется
— шар отскакивает обратно. Второй шар
движется в ту же сторону, в которую
двигался первый шар до удара, но с меньшей
скоростью, т.е. v’2<v1
(рис.
21);
г)
m2>>m1
(например,
столкновение шара со стеной). Из уравнений
(15.8) и (15.9) следует, что v’1=-v1,
v’22m1v1/m20.

2) При
m1=m2
выражения
(15.6) и (15.7) будут иметь вид
v’1=v2,
v’2=v1,
т. е. шары равной
массы «обмениваются» скоростями.
Абсолютно
неупругий удар — столкновение
двух тел, в результате которого тела
объединяются, двигаясь дальше как единое
целое.

Продемонстрировать
абсолютно неупругий удар можно с
помощью шаров из пластилина (глины),
движущихся навстречу друг другу (рис.
22).
Если
массы шаров m1
и
m2,
их скорости до удара v1
и
v2,
то,
используя закон сохранения импульса,
можно записать

Если
шары движутся навстречу друг другу, то
они вместе будут продолжать двигаться
в ту сторону, в которую двигался шар,
обладающий большим импульсом. В частном
случае если массы шаров равны (m1=m2),
то
v
= (v1+v2)/2.
Выясним, как
изменяется кинетическая энергия
шаров при центральном абсолютно
неупругом ударе. Так как в процессе
соударения шаров между ними дей-
30
ствуют силы,
зависящие не от самих деформаций, а от
их скоростей, то мы имеем дело с силами,
подобными силам трения, поэтому закон
сохранения механической энергии не
должен соблюдаться. Вследствие деформации
происходит «потеря» кинетической
энергии, перешедшей в тепловую или
другие формы энергии. Эту «потерю» можно
определить по разности кинетической
энергии тел до и после удара:
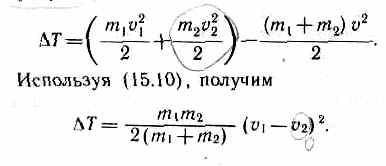
Если
ударяемое тело было первоначально
неподвижно (v2=0),
то

Когда
m2>>m1
(масса
неподвижного тела очень большая), то
v<<v1
и
почти
вся кинетическая энергия тела при ударе
переходит в другие формы энергии.
Поэтому, например, для получения
значительной деформации наковальня
должна быть массивнее молотка.
Наоборот, при забивании гвоздей в стену
масса молотка должна быть гораздо
большей (m1>>m2),
тогда
vv1
и
практически вся энергия затрачивается
на возможно большее перемещение гвоздя,
а не на остаточную деформацию стены.
Абсолютно неупругий
удар — пример того, как происходит
«потеря» механической энергии под
действием диссипативных сил.
Контрольные
вопросы
• В чем различие
между понятиями энергии и работы?
• Как найти
работу переменной силы?
• Какую работу
совершает равнодействующая всех сил,
приложенных к телу, равномерно движущемуся
по окружности?
• Что такое
мощность? Вывести ее формулу.
• Дайте определения
и выведите формулы для известных вам
видов механической энергии. • Какова
связь между силой и потенциальной
энергией?
• Почему изменение
потенциальной энергии обусловлено
только работой консервативных сил?
• В чем заключается
закон сохранения механической энергии?
Для каких систем он выполняется?
• Необходимо
ли условие замкнутости системы для
выполнения закона сохранения механической
энергии?
• В чем физическая
сущность закона сохранения и превращения
энергии? Почему он является фундаментальным
законом природы?
• Каким свойством
времени обусловливается справедливость
закона сохранения механической энергии?
• Что такое
потенциальная яма? потенциальный барьер?
• Какие заключения
о характере движения тел можно сделать
из анализа потенциальных кривых?
• Как
охарактеризовать положения устойчивого
и неустойчивого равновесия? В чем их
различие?
• Чем отличается
абсолютно упругий удар от абсолютно
неупругого?
• Как определить
скорости тел после центрального абсолютно
упругого удара? Следствием каких законов
являются эти выражения?
31
Задачи
3.1. Определить:
1) работу поднятия груза по наклонной
плоскости; 2) среднюю и 3) максимальную
мощности подъемного устройства, если
масса груза 10 кг, длина наклонной
плоскости 2 м, угол ее наклона к горизонту
45°, коэффициент трения 0,1 и время подъема
2 с. [1) 170 Дж; 2) 85 Вт; 3) 173 Вт |
3.2. С башни высотой
35 м горизонтально брошен камень массой
0,3 кг. Пренебрегая сопротивлением
воздуха, определить: 1) скорость, с которой
брошен камень, если через 1 с после начала
движения его кинетическая энергия 60
Дж; 2) потенциальную энергию камня через
1 с после начала движения. [1) 17,4 м/с; 2)
88,6 Дж ]
3.3. Пренебрегая
трением, определить наименьшую высоту,
с которой должна скатываться тележка
с человеком по желобу, переходящему в
петлю радиусом 10 м, чтобы она сделала
полную петлю и не выпала из желоба. [25
м]
3.4.
Пуля массой m=
10 г, летевшая горизонтально со скоростью
v
= 500 м/с, попадает в баллистический
маятник длиной l=
1 м и массой М = 5 кг и застревает в нем.
Определить угол отклонения маятника.
[ 18°30′ ]
3.5.
Зависимость потенциальной энергии
частицы в центральном силовом поле от
расстояния r
до
центра
поля задается выражением П(r)
=A/r2
-B/r,
где А
и
В —
положительные постоянные.
Определить
значение r0,
соответствующее
равновесному положению частицы. Является
ли это положение положением устойчивого
равновесия? [r0
= 2А/В]
3.6.
При центральном абсолютно упругом ударе
движущееся тело массой m1
ударяется
в покоящееся тело массой m2,
в результате чего скорость первого тела
уменьшается в n=
1,5 раза. Определить: 1) отношение m1/m2;
2)
кинетическую энергию T’2,
с
которой начнет двигаться второе
тело, если первоначальная кинетическая
энергия первого тела T1
=
1000 Дж. [ 1) 5; 2) 555 Дж ]
3.7.
Тело массой m1=4
кг движется со скоростью v1=3
м/с
и ударяется о неподвижное тело такой
же массы. Считая удар центральным и
неупругим, определить количество
теплоты, выделившееся при ударе. [9 Дж ]
* У. Гамильтон
(1805—1865) — ирландский математик и
физик.
Соседние файлы в папке Трофимова
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью ![]() попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
Обозначим скорость ящика с застрявшей в нем пулей через ![]() Тогда по закону сохранения импульса
Тогда по закону сохранения импульса
![]()
При застревании пули в песке произошла потеря механической энергии:
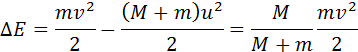
Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
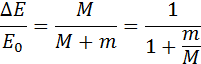
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.
При m << M
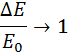
почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M
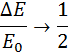
во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение
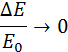
Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
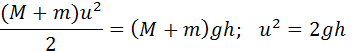
где h – максимальная высота подъема маятника. Из этих соотношений следует:
![]()
Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.
|
|
|
Рисунок 1.21.1. Баллистический маятник |
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
|
|
|
Рисунок 1.21.2. Абсолютно упругий центральный удар шаров |
В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
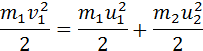
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
![]()
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u1 и u2 шаров после столкновения:
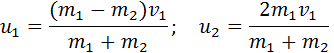
В частном случае, когда оба шара имеют одинаковые массы (m1 = m2), первый шар после соударения останавливается (u1 = 0), а второй движется со скоростью u2 = υ1, т. е. шары обмениваются скоростями (и, следовательно, импульсами).
Если бы до соударения второй шар также имел ненулевую скорость (υ2 ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ2 относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ1‘ = υ1 – υ2. Определив по приведенным выше формулам скорости u1 и u2 шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.
Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.
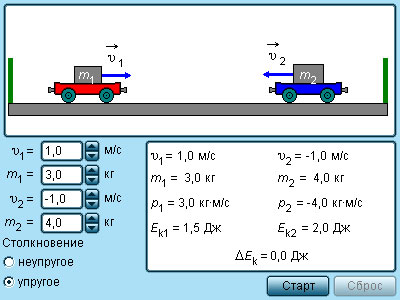 |
|
Модель. Упругие и неупругие соударения. |
Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.
Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).
|
|
|
Рисунок 1.21.3. Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние |
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей ![]() и
и ![]() после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости
после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости ![]() налетающего шара. Если массы шаров одинаковы, то векторы скоростей
налетающего шара. Если массы шаров одинаковы, то векторы скоростей ![]() и
и ![]() шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m1 = m2 = m эти законы принимают вид:
шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m1 = m2 = m эти законы принимают вид:
![]()
Первое из этих равенств означает, что векторы скоростей ![]() ,
, ![]() и
и ![]() образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами
образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами ![]() и
и ![]() равен 90°.
равен 90°.
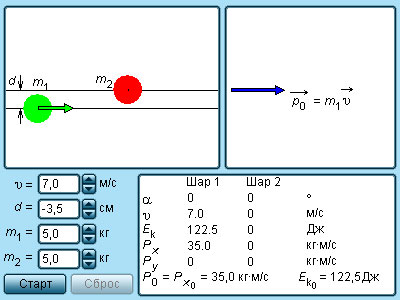 |
|
Модель. Соударения упругих шаров. |
Упругое соударение
Соударение — это столкновение двух тел.
При соприкосновении тела обмениваются энергией и импульсом.
После соударения они двигаются со скоростями, которые отличаются по направлению и величине от их скоростей до столкновения.
При лобовом центральном соударении центры масс обоих тел двигаются вдоль одной линии.
Силы взаимодействия, возникающие при соударении, параллельны направлению движения.
Если применить к такой системе двух тел закон сохранения импульса, то полный импульс системы будет равен алгебраической сумме импульсов обоих тел.
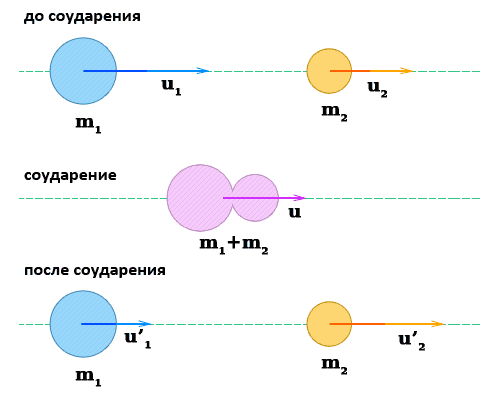
Упругое соударение
При упругом соударении на протяжении кратковременного соприкосновения тела двигаются с общей скоростью,
затем они разлетаются и продолжают двигаться с разными скоростями.
Если
| m1 | масса первого тела, | кг |
|---|---|---|
| m2 | масса второго тела, | кг |
| u1 | скорость первого тела до соударения, | метр/секунда |
| u2 | масса второго тела до соударения, | метр/секунда |
| u`1 | скорость первого тела после соударения, | метр/секунда |
| u`2 | масса второго тела после соударения, | метр/секунда |
то из закона сохранения импульса следует
[ m_1 u_1 + m_2 u_2 = m_1 u`_1 + m_2 u`_2 ]
или
[ m_1 (u_1 – u`_1) = m_2 (u`_2 – u_2) ]
Из закона сохранения энергии получаем
[ frac{m_1 u_1 ^2}{2} + frac{m_2 u_2 ^2}{2} = frac{m_1 u`_1 ^2}{2} + frac{m_2 u`_2 ^2}{2} ]
или
[ m_1 (u_1 ^2 – u`_1 ^2) = m_2 (u`_2 ^2 – u_2 ^2) ]
подставив формулу разность квадратов получим
[ m_1 (u_1 – u`_1)(u_1 + u`_1) = m_2 (u`_2 – u_2)(u`_2 + u_2) ]
воспользовавшись законом сохранения импульса, находим
[ u_1 + u`_1 = u`_2 + u_2 ]
Сумма скоростей до и после соударения одинакова при любом соударении тел.
Из формулы (6) следует
[ u`_2 = u`_1 + u_1 – u_2 ]
[ u`_1 = u`_2 + u_2 – u_1 ]
Подставив эти выражения в видоизмененный закон сохранения импульса, получим
[ m_1 (u_1 – u`_1) = m_2 (u`_1 + u_1 – u_2 – u`_2) ]
[ m_1 (u_1 – u_2 – u`_2 + u_1) = m_2 (u`_2 – u_2) ]
откуда, разрешив относительно u`1 и u`2 найдем
[ u`_1 = frac{ (m_1 – m_2) u_1 + 2 m_2 u_2 }{ m_1 + m_2 } ]
[ u`_2 = frac{ (m_2 – m_1) u_2 + 2 m_1 u_1 }{ m_1 + m_2 } ]
Упругое соударение, вычислить скорости тел после упругого соударения
Упругое соударение |
стр. 477 |
|---|
как определить скорости тел после центрального абсолютного упругого удара?
_Д_Е_Т_К_О___К_О_Н_Ф_Е_Т_К_О_
Ученик
(71),
закрыт
2 года назад
как определить скорости тел после центрального абсолютного упругого удара?следствием каких законов являются эти выражения?
Дарья Чарикова
Просветленный
(34703)
12 лет назад
при абсолютно упругом ударе энергия не теряется. Т. е. можно использвать и закон сохранения импульса, и закон сохранения механической энергии. Получаем 2 уравнения
Сумма кинетических энергий тел до удара = сумме кинетических энергий тел после удара
Импульс системы до удара = импульсу системы после удара
из этих двух уравнений ищутся 2 неизвестные скорости