
reshalka.com
ГДЗ Физика 7-9 классы сборник вопросов и задач к учебнику Перышкина автор Марон. Прямолинейное равноускоренное движение. Ускорение. Перемещение при прямолинейном равноускоренном движении. Номер №1460
Решение 1
С каким ускорением движется Автомобиль “Ока”, если его скорость увеличивается от 0 до 100 км/ч за 30 с ? Какой путь пройдет автомобиль за время разгона?
Дано:
t = 30 c;
v
0
=
0
м/с;
v = 100 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 27,8 м/с.
Решение:
Уравнение скорости:
v
=
v
0
+
a
t
;
a
=
v
–
v
0
t
;
a
=
27
,
8
−
0
30
=
0
,
93
м
/
с
2
;
S
=
a
t
2
2
;
S
=
0
,
93
∗
30
2
2
=
418
,
5
м.
Ответ: 0,93
м
/
с
2
; 418,5 м.
Решение 2
Гоночный автомобиль движется 3,4 с равноускоренно из состояния покоя. Скорость после разгона составила 100 км/ч. Найдите ускорение и пройденный путь.
Дано:
t = 3,4 c;
v
0
=
0
м/с;
v = 100 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 27,8 м/с.
Решение:
Уравнение скорости:
v
=
v
0
+
a
t
;
a
=
v
–
v
0
t
;
a
=
27
,
8
−
0
3
,
4
=
8
,
2
м
/
с
2
;
S
=
a
t
2
2
;
S
=
8
,
2
∗
3
,
4
2
2
=
47
,
4
м.
Ответ: 8,2
м
/
с
2
; 47,4 м.
Решение 3
С каким ускорением движется Автомобиль ВАЗ, если его скорость увеличивается от 0 до 100 км/ч за 19 с ? Какой путь пройдет автомобиль за время разгона?
Дано:
t = 19 c;
v
0
=
0
м/с;
v = 100 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 27,8 м/с.
Решение:
Уравнение скорости:
v
=
v
0
+
a
t
;
a
=
v
–
v
0
t
;
a
=
27
,
8
−
0
19
=
1
,
46
м
/
с
2
;
S
=
a
t
2
2
;
S
=
1
,
46
∗
19
2
2
=
269
м.
Ответ: 1,46
м
/
с
2
; 269 м.
Решение 4
Гепард за 2 с развивает скорость до 72 км/ч. Найдите ускорение и пройденный за это время путь.
Дано:
t = 2 c;
v
0
=
0
м/с;
v = 72 км/ч.
Найти:
a − ?
S − ?
СИ:
v = 20 м/с.
Решение:
Уравнение скорости:
v
=
v
0
+
a
t
;
a
=
v
–
v
0
t
;
a
=
20
−
0
2
=
10
м
/
с
2
;
S
=
a
t
2
2
;
S
=
10
∗
2
2
2
=
20
м.
Ответ: 10
м
/
с
2
; 20 м.
Решение 5
Конькобежец − спринтер дистанцию 50 м пробегает за 8,5 с. С каким ускорением двигался спортсмен? Какая установилась скорость после разгона?
Дано:
t = 8,5 c;
S = 50 м;
v
0
=
0
м/с.
Найти:
a − ?
v − ?
Решение:
Уравнение движения:
S
=
v
0
t
+
a
t
2
2
;
Так как спорстмен начинает движение, то
v
0
=
0
м/с.
S
=
a
t
2
2
;
2
S
=
a
t
2
;
a
=
2
S
t
2
;
a
=
2
∗
50
8
,
5
2
=
1
,
38
м
/
с
2
;
v = at;
v = 1,38 * 8,5 = 11,73 м/с.
Ответ: 1,38
м
/
с
2
; 11,73 м/с.
Решение 6
Легкоатлет− спринтер на дистанции 40 м разогнался до 39,6 км/ч. Найдите время его разгона и ускорение.
Дано:
S = 40 м.
v = 39,6 км/ч;
v
0
=
0
м/с.
Найти:
a − ?
t − ?
СИ:
v = 11 м/с.
Решение:
S
=
v
0
+
v
2
∗
t
;
2
S
=
(
v
0
+
v
)
∗
t
;
t
=
2
S
v
0
+
v
;
t
=
2
∗
40
0
+
11
=
7
,
3
с;
v
=
v
0
+
a
t
;
Так как
v
0
=
0
м/с, то v = at;
a
=
v
t
;
a
=
11
7
,
3
=
1
,
5
м
/
с
2
.
Ответ: 1,5
м
/
с
2
; 7,3 с.
Решение 7
Велосипедист за 15 с проехал путь 200 м. Найдите ускорение и скорость после разгона.
Дано:
t = 15 c;
S = 200 м;
v
0
=
0
м/с.
Найти:
a − ?
v − ?
Решение:
Уравнение движения:
S
=
v
0
t
+
a
t
2
2
;
Так как велосипедист начинает движение, то
v
0
=
0
м/с.
S
=
a
t
2
2
;
2
S
=
a
t
2
;
a
=
2
S
t
2
;
a
=
2
∗
200
15
2
=
1
,
78
м
/
с
2
;
v = at;
v = 1,78 * 15 = 26,7 м/с.
Ответ: 1,78
м
/
с
2
; 26,7 м/с.
Решение анализ
Среди 3−х автомобилей с наибольшим ускорением двигался гоночный автомобиль, затем автомобиль Ваз. Наименьшее ускорение имеет автомобиль “Ока”, т.к. ему нужно больше времени для разгона до 100 км/ч.
Среди 3−х спортсменом с наибольшим ускорением двигался велосипедист, затем легкоатлет−спринтер. Наименьшее ускорение имеет конькобежец − спринтер.
Ускорение гепарда выше ускорения автомобилей и спортсменов.
Скорость, время и ускорение
Расчеты
Три этих физических величины взаимосвязаны между собой процессом движения. Если известны две из этих величин, можно найти третью.
Скорость тела при условии равноускоренного прямолинейного движения определяем по формуле:
V = V0 + а*t
V0 — начальная скорость (при t = 0);
а — ускорение;
t — время.
Итак, чтобы найти скорость, к начальной скорости прибавляем произведение ускорения на время.
Если V0 = 0, то V = а*t.
Чтобы найти время, нужно вначале найти разность между скоростью в данный момент и начальной скоростью, затем полученный результат разделить на ускорение.
t = (V — V0) / а
Ускорение показывает изменение скорости движущегося тела, рассчитывается по двум скоростям и времени. Чтобы вычислить ускорение, следует найти разницу между скоростью в данный момент и начальной скоростью, затем все это разделить на время.
При ускорении:
а = (V — V0) / t
При торможении:
а = (V0 — V) / t
Ускорение — величина векторная, которая задается не только числом, но и направлением, измеряется в метрах в секунду (м/с2).
Чтобы рассчитать среднее ускорение, находим разницу между начальной и конечной скоростями Δv, полученный результат делим на разницу между временем Δt.(начальным и конечным) :
а = Δv / Δt
Быстро и правильно рассчитать величину скорости, ускорения или найти время вам поможет онлайн калькулятор.
Расчет скорости, времени и ускорения
Если движение связано с постоянным ускорением, в этой статье мы можем изучить простой метод определения средней скорости на графике времени ускорения.
Чтобы узнать, как найти среднюю скорость на графике времени ускорения, мы должны знать, что Vсредний объекта измеряется путем деления общего изменения положения, наблюдаемого в движении, на время, необходимое для завершения этого движения. Аналогично на графике АТ путем измерения наклона начальной и последней точек графика.
Теперь дайте нам знать, как найти среднюю скорость на графике времени разгона подробно.
Как найти среднюю скорость на графике положение-время
Чтобы найти среднюю скорость на графике PT, мы должны знать следующие основные идеи:
В общем, мы знаем, что Vсредний рассчитывается исходя из критериев положения и времени; эти два важны при измерении Vсредний, Итак, что мы можем сделать, так это присвоить значения и пометить ось, а затем построить ее. Нарисуйте наклон кривой, отметьте любые две точки и рассмотрите начальную и конечную точки. Значение этого наклона будет Vсредний.
Теперь дайте нам знать о графике времени разгона.
График ускорения-времени
В физике существует множество графиков отношений, позволяющих быстро находить значения конкретных величин.
Графики времени ускорения – один из тех важнейших графиков. Нам необходимо преобразовать график скорости-времени в график времени ускорения, чтобы узнать конкретные значения, т. Е. Путем нахождения производной определенных значений, таких как средняя скорость. Мы можем взять наклон касательной к кривой, проведенной на графике в любой точке.
Теперь, когда мы узнали о графике AT, расскажите нам о его особенностях.
Особенности графика времени разгона после средней скорости.
Существенные особенности графика времени ускорения в соответствии с расчетом средней скорости следующие:
- Чтобы найти Vсредний на графике AT, после выполнения всех маркировок, построения графиков и объединения значений.
- Нарисуйте уклон, и этот уклон называется рывком. Здесь значения наклона будут равны полной средней скорости.
- В случае постоянного ускорения s должен вычислить значение наклона для полученной горизонтальной линии, которая называется средней скоростью.

После всего этого пришло время увидеть различные аспекты этого подхода.
Аспекты графика времени ускорения и средней скорости
Ниже можно увидеть различные аспекты графика времени ускорения и средней скорости.
- График времени ускорения для всех объектов, движущихся с постоянной V, будет аналогичным.
- Объектом может быть большой самолет или маленький муравей, и график будет таким же, но с разными значениями.
- График будет коллинеарен по оси x (горизонтальная линия).
- Буква V будет одинаковой для всех этих объектов в их справочнике.
Как найти среднюю скорость на графике времени разгона?
Чтобы найти букву V на графике времени ускорения, необходимо выполнить определенные действия.
Прежде всего, мы должны отметить первоначальный скорость и постоянное ускорение тела в движении.
Затем используйте это ускорение и узнайте конечную скорость.
Найдя все значения, нанесите их на график AT.
- Рассмотрим любые две точки и нарисуем наклон.
- Затем измерьте площадь под этой кривой и используйте формулу
- Формула включает расстояние и время, используется формула средней скорости и выводится из термина, используемого для измерения средних значений.
- Позже проводятся касательная и наклон, чтобы получить значение требуемого V.
Таким образом, мы можем найти среднюю скорость на графике времени ускорения.
Связь между графиком времени ускорения и средней скоростью
Чтобы найти V., мы иногда используем график времени разгона. Есть два критических случая ускорения при измерении средней скорости.
- И средняя скорость величины, и ускорение не зависят друг от друга.
- Если ускорение больше, то изменение скорости будет максимальным, но это не говорит о скорости в конкретный момент времени. Здесь мы получаем общее значение скорости, называемое средней скоростью.
- Переходя к другому случаю, если ускорение постоянное, график AT будет линейным. Здесь средняя скорость будет одинаковой во всех точках.
Теперь давайте решим некоторые проблемы, чтобы лучше их понять.
Проблемы с нахождением средней скорости по графику времени разгона.
Вот несколько проблем, которые необходимо решить, чтобы лучше понять концепцию.
Проблема 1
The начальная скорость тела, движущегося в положительном направлении равен нулю, но при движении его ускорение равно 9 м/с; найти его скорость будет 8с?
Решение:
∆V = a∆t
∆V = (9.8 м / с) (1.0 с)
∆V = 9.8 м / с
Теперь нужно рассчитать окончательную скорость.
∆V = a∆t
∆V = (9 м / с) (8 с)
∆V = 72 м / с
Если мы найдем это на графике времени ускорения, мы найдем среднюю скорость, вычислив площадь под кривой.
Это одна из фундаментальных проблем, которые нужно решить на V на AT-графе.
Различные подходы к определению средней скорости
Среднюю скорость можно найти в основном двумя способами, которые показаны ниже:
- С помощью специальной формулы мы можем найти среднюю скорость разными способами, используя расстояние или изменение положения объекта на пути в определенное время.
- Мы даже можем использовать расчет, чтобы определить требуемую среднюю скорость.
- Еще один способ узнать Vсредний использует определенные графики, такие как график положения-времени, график скорости-времени и даже график ускорения-времени.
- Построив значения данных на графике, а затем выполнив определенные шаги, можно рассчитать среднюю скорость.
Упомянутые ранее подходы являются основными методами, используемыми для определения средней скорости.
Чтобы узнать о мгновенная скорость
Часто задаваемые вопросы | FAQs
Какая средняя скорость зависит от ускорения и времени?
На графике времени ускорения средняя скорость тела вычисляется с учетом двух точек на графике.
Если ускорение переменное, есть небольшие трудности с измерением средней скорости на графике времени ускорения. Тем не менее, если ускорение постоянное, Vavg можно найти, сложив скорость тела в начале и в конце по определенной формуле.
Как найти среднюю скорость по ускорению и времени?
Средняя скорость, которую обычно обозначают в Vсредний может быть дано следующим образом с использованием ускорения и времени.
Мы используем ускорение, обозначаемое как a, и время как t, с помощью расстояния и времени. Мы можем выполнить определенные шаги и вывести формулу с помощью, мы можем измерить Vсредний тела; формула приведена ниже.
S = vi + ½ в2
vсредний = s / t = vi + ½ в2
vсредний = Vi + ½ (вf – vi)
vсредний = (см.f – vi)
То есть ускорение, умноженное на время, равно общему изменению скорости.
Что такое график скорости-времени?
Даже график скорости-времени – один из важнейших графиков в физике.
Это реальное представление изменения скорости объекта во время движения в зависимости от затраченного времени. Графики могут быть любого типа в зависимости от постоянного и переменного аспектов. Если скорость быстрая, линия графика не будет горизонтальной по отношению к какой-либо оси, и наоборот, если есть какой-либо изменяемый член, тогда линия графика будет параллельна оси.
Что такое график ускорения-времени?
График времени ускорения включает ускорение и время соответственно по осям x и y.
График зависимости ускорения от времени строится в зависимости от времени, затраченного объектом на движение по линейной траектории. На этом графике можно найти среднюю скорость в зависимости от постоянного и переменного ускорения. Значение графика представлено в виде y = a (t). Уникальная особенность этого графика в том, что мы можем найти как положительные, так и отрицательные значения скорости и даже ускорения.
Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.
Примеры равноускоренного движения:
- разгон самолета перед взлетом;
- падающая с крыши сосулька;
- торможение лыжника на горном склоне;
- разгоняющийся на склоне сноубордист;
- свободное падение в результате прыжка с парашютом;
- камень брошенный под углом к горизонту;
Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Равноускоренное движение: формулы
Формула для скорости при равноускоренном движении:
Vк=Vн+at
где: Vк — конечная скорость тела,
Vн — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.
Формула для ускорения при равноускоренном движении:
a=(Vк-Vн)/t
Во время движения тела ускорение остается постоянным.
Задача 1
Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.
Формула расстояния при равноускоренном движении
- Если известны время, скорость начальная и скорость конечная
S = t*(Vн+ Vк)/2
- Если известны время, скорость начальная и ускорение
S = Vнt + at2/2 = t*(Vн + at/2)
где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
2аS = Vк2−Vн2
где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.
Задача 2
Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.
Равноускоренное движение: графически
График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.
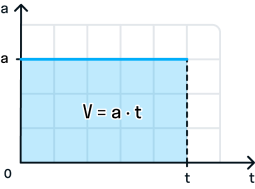
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.
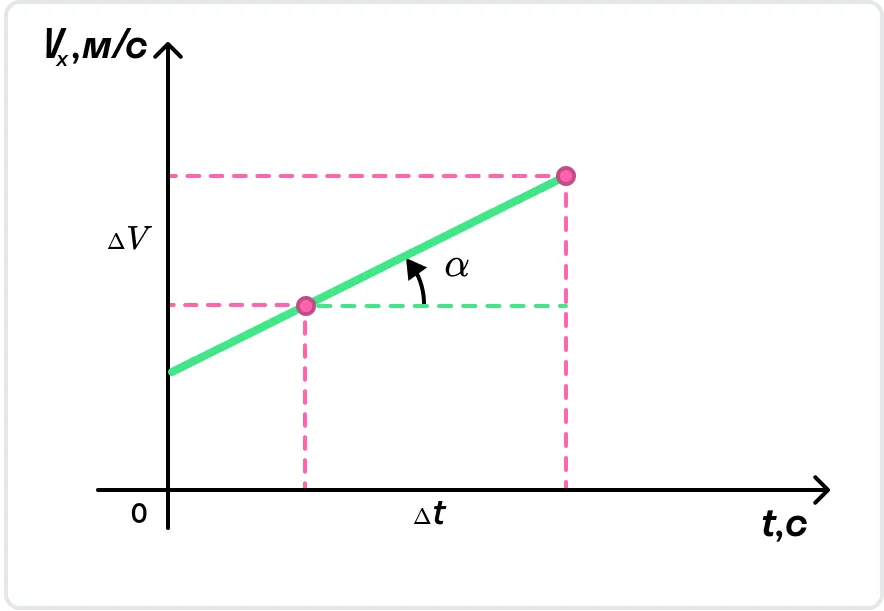
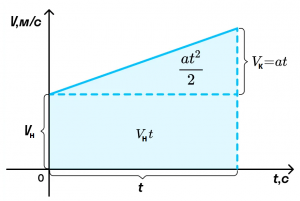
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника Vнt и треугольника at2/2. Получим: S = Vнt + at2/2.
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.
Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.
Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = Vк2−Vн2
Получим: а = (Vк2−Vн2 )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = Vнt + at2/2.
Получаем: x(t) = 3t + 1,5t2
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*22 =6+6=12 м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.
Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:
- Конвертер единиц измерения расстояния (длины)
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
Время на прочтение
3 мин
Количество просмотров 9.6K
Немного теории.
Для начала разберемся с тем, что такое лошадиные силы и устроим небольшой экскурс в школьную физику.
1 л.с. – это мощность, затрачиваемая при вертикальном подъёме груза массой 75 кг со скоростью 1 м/с.
Как известно, мощность показывает, какую работу совершает тело в единицу времени:
Работа равна произведению силы на перемещение: A = F*S. Учитывая, что скорость V=S/t, получим:
Получаем формулу для перевода лошадиных сил в принятую в международной системе СИ единицу измерения мощности – Ватт:
Перейдем к основной части, а именно – к техническим характеристикам автомобиля.
Некоторые характеристики и расчёты будут приводиться приближенно, поскольку мы не претендуем на умопомрачительную точность расчетов, важнее понять физику и математику процесса.
m = 2 тонны = 2000 кг – масса автомобиля (масса авто 1940 кг, считаем что в ней водитель массой 60 кг и больше ничего/никого).
P = 670 л.с. (по паспорту 625 л.с., но реально мощность выше – измерено на динамометрическом стенде в ролике DSC OFF https://www.youtube.com/watch?v=ysg0Depmyjc. В этой статье мы ещё обратимся к замерам отсюда.)
Разгон 0-100 км/ч: 3.2-3.3 с (по паспорту, замерам)
Разгон 100-200 км/ч: 7.5-7.6 с (по паспорту, замерам)
Мощность двигателя генерируется на маховике, потом через сцепление передается в КПП, далее через дифференциалы, привода, карданный вал передается на колёса. В результате эти механизмы поглощают часть мощности и итоговая мощность, поставляемая к колесам, оказывается меньше на 18-28%. Именно мощность на колесах определяет динамические характеристики автомобиля.
У меня нет сомнений в гениальности инженеров БМВ, но, для начала, возьмем для удобства потери мощности 20%.
Вернемся к нашим физическим баранам. Для вычисления разгона нам нужно связать мощность со скоростью и временем разгона. Для этого воспользуемся вторым законом Ньютона:
Вооружившись этими знаниями, получим конечную формулу:
Выражая отсюда t, получим итоговую формулу для вычисления разгона:
На самом деле в паспорте автомобиля указывается максимальная мощность, достигаемая двигателем при определенном числе оборотов. Ниже приведена зависимость мощности двигателя от числа оборотов (синяя линия). Строго говоря, параметры этой кривой зависят от номера передачи, так что для определенности скажем, что график для 5й передачи.
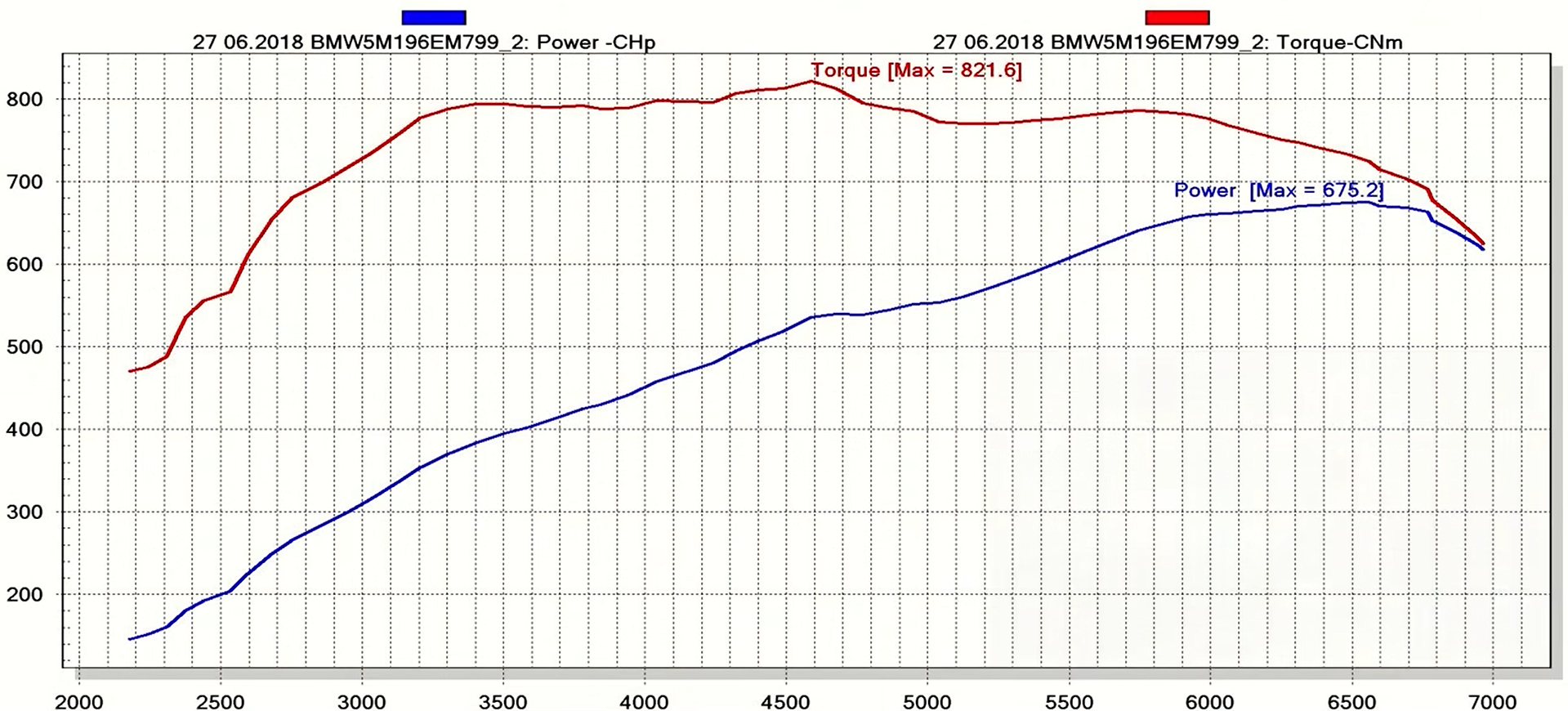
Главное, что мы должны усвоить из этого графика – мощность автомобиля не постоянна во время движения, а увеличивается по мере роста оборотов двигателя.
Перейдем к расчету разгона от 0 до 100 км/ч. Переведем скорость в м/с:
При разгоне от 0 до 100 км/ч автомобиль практически сразу переключается с первой передачи на вторую, и при достижении около 90 км/ч переключается на третью. Будем считать, что на всём протяжении разгона автомобиль разгоняется на второй передаче, причем максимальная мощность будет меньше 670 л.с., поскольку передача ниже пятой. Возьмём в качестве начальной мощности при 0 км/ч мощность 150 л.с. (при 2000 об/мин), конечную – 600 л.с. (7000 об/мин):
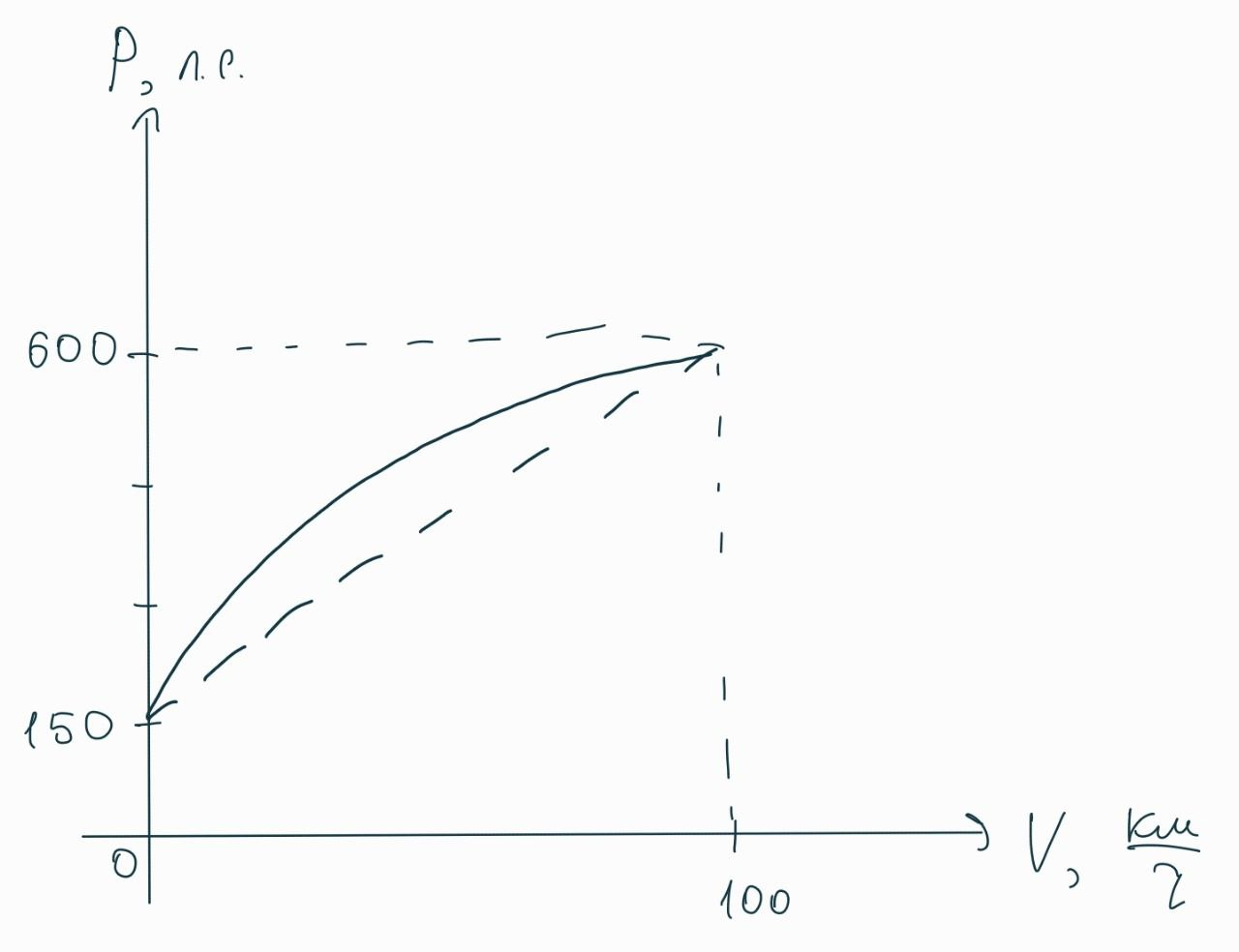
Чтобы не считать сложные интегралы для вычисления средней мощности, скажем следующие слова: учитывая приближенный характер наших расчетов, проскальзывание авто при ускорении, а также сопротивление воздуха (хотя при разгоне от 0 до 100 оно играет не такую большую роль, как при разгоне до 200 км/ч), будем считать, что мощность зависит от скорости линейно, тогда средняя мощность при разгоне от 0 до 100 км/ч составляет:
Пришло время учесть потери мощности, о которых было сказано ранее, а заодно перевести мощность в кВт (1 кВт = 1000 Вт) для удобства. Потери мощности 20%, значит эффективность 80%=0.8:
Теперь подставляем всё в конечную формулу:
Получили довольно близкий к “паспортным” 3.3 с результат, ура! Специально не стал ничего дополнительно подгонять, дабы подчеркнуть приближенный характер расчёта, хотя это было довольно просто сделать, взяв, например, чуть больше мощность.
Теперь, ради интереса и проверки самих себя, вычислим разгон 100-200 км/ч.
С ростом скорости растёт трение воздуха, для движения используются более высокие передачи КПП (3-я, 4-я, 5-я), но при этом уменьшается проскальзывание колес. Так что оставим среднюю мощность 375 л.с.
Так делать конечно же нельзя! После 2-й передачи двигатель работает на “комфортных” для себя оборотах 4000-7000 об/мин, поэтому средняя мощность будет гораздо выше, поскольку выше будет начальная мощность для каждой передачи. Здесь уже не получится считать, что автомобиль едет только на 4-й передаче на всем протяжении разгона, но можно считать, что он проехал одинаковые промежутки времени на 3-й, 4-й и 5-й передаче, и пусть график зависимости мощности от числа оборотов для них одинаков, поэтому построим общую условную кривую зависимости мощности от скорости:
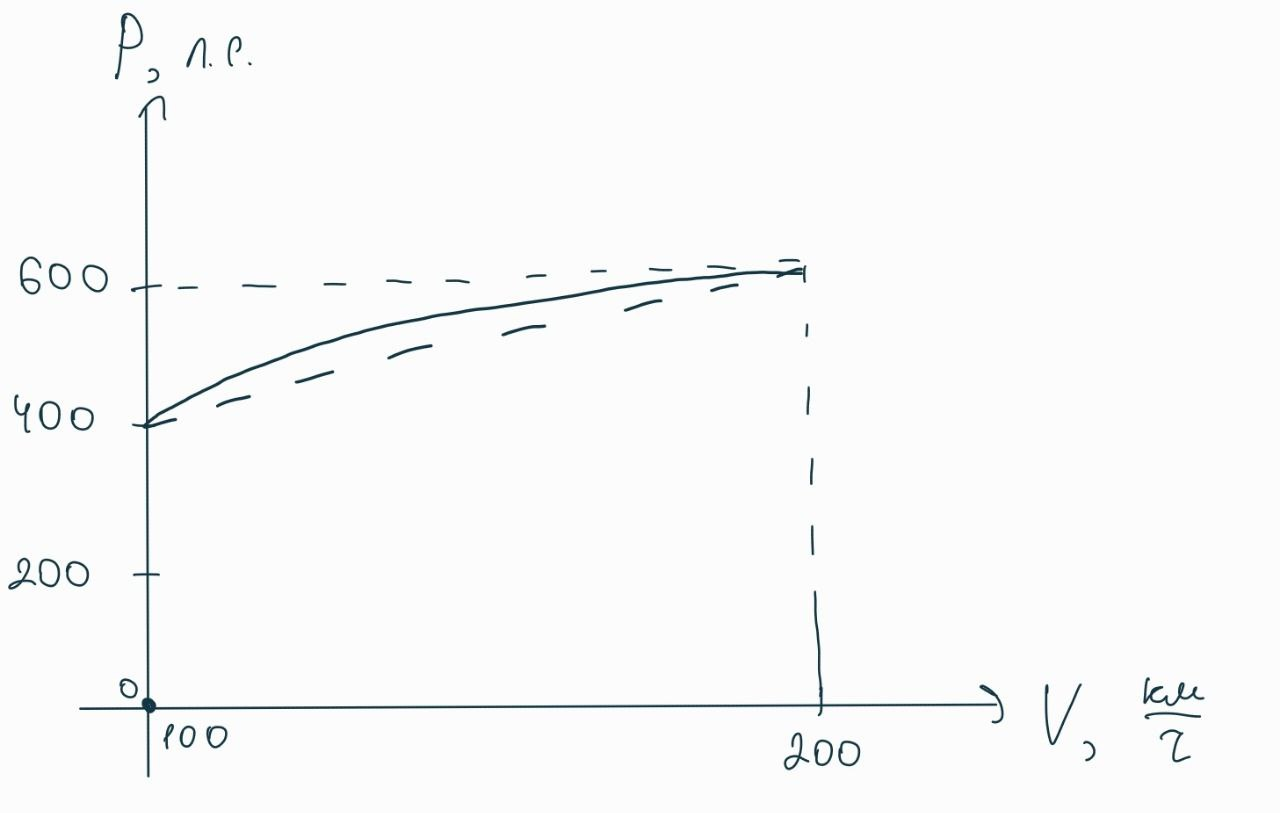
Опять же, считаем для простоты зависимость мощности от скорости линейной, тогда получаем среднюю и реальную мощность:
Тогда итоговое время разгона 100-200 км/ч:
Время разгона “по паспорту” 7.6 с. И снова мы оказались близко к истине!
P.S. не хочу объяснять, откуда взялось (V^2 – V_0^2), можете повыводить на досуге 🙂
Ну и в общем-то всё. Приведенные рассуждения и вычисления не претендуют на истину в последней инстанции и большую точность, но показывают, что зная “школьные” формулы по физике, можно решать такие интересные задачки, связанные с жизнью.
