Как найти скорость потока через давление

Как найти скорость потока через давление

Рисунок из «Гидродинамики» Д. Бернулли: из-за течения по трубе, компенсирующего расход через правое отверстие О, давление в трубе меньше, чем в сосуде слева.

Механика сплошных сред
BernoullisLawDerivationDiagram.svg
Сплошная среда

Классическая механика

Закон сохранения массы · Закон сохранения импульса

Теория упругости

Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость

Гидродинамика

Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение

Основные уравнения

Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука

См. также: Портал:Физика

Зако́н Берну́лли[1] (также уравне́ние Берну́лли[2][3], теоре́ма Берну́лли[4][5] или интегра́л Берну́лли[2][6][7]) устанавливает зависимость между скоростью стационарного потока жидкости и её давлением. Согласно этому закону, если вдоль линии тока давление жидкости повышается, то скорость течения убывает, и наоборот. Количественное выражение закона в виде интеграла Бернулли является результатом интегрирования уравнений гидродинамики идеальной жидкости[2] (то есть без вязкости и теплопроводности).

История[править | править код]

Для случая несжимаемой жидкости результат, эквивалентный современному уравнению Бернулли, был опубликован в 1738 году Даниилом Бернулли[K 1]. В современном виде интеграл был опубликован Иоганном Бернулли в 1743 году[11] для случая несжимаемой жидкости, а для некоторых случаев течений сжимаемой жидкости — Эйлером в 1757 году[12].

Интеграл Бернулли в несжимаемой жидкости[править | править код]

Полное давление
Размерность {displaystyle L^{-1}MT^{-2}}
Единицы измерения
СИ Дж/м3 = Па
СГС эрг/см3
Примечания
Постоянно вдоль линии тока стационарного течения несжимаемой жидкости.

Для стационарного течения несжимаемой жидкости уравнение Бернулли может быть получено как следствие закона сохранения энергии. Закон Бернулли утверждает, что величина {displaystyle rho v^{2}/2+rho gh+p} сохраняет постоянное значение вдоль линии тока:

{displaystyle {frac {rho v^{2}}{2}}+rho gh+p={text{const}}.}

Здесь

rho  — плотность жидкости;
v — скорость потока;
h — высота;
p — давление;
g — ускорение свободного падения.

Элементарный вывод уравнения Бернулли из закона сохранения энергии

BernoullisLawDerivationDiagram.png

Элементарный вывод уравнения Бернулли из закона сохранения энергии приведён, например, в учебнике Д. В. Сивухина[13]. Рассматривается стационарное движение жидкости вдоль линии тока, изображённое на рисунке. Слева на объем жидкости, первоначально заключённый между двумя сечениями A_{1} и A_{2}, действует сила {displaystyle F_{1}=p_{1}A_{1}}, а справа — противоположного направления сила {displaystyle F_{2}=-p_{2}A_{2}}. Скорость v и давление p в сечениях 1 и 2, а также их площади обозначены нижними индексами 1 и 2. За бесконечно малое время Delta t левая граница этого объёма жидкости сместилась на малое расстояние {displaystyle s_{1}=v_{1}Delta t}, а правая — на расстояние {displaystyle s_{2}=v_{2}Delta t}. Работа, совершённая силами давления, равна:

{displaystyle W=F_{1}s_{1}+F_{2}s_{2}=Delta tleft(v_{1}A_{1}p_{1}-v_{2}A_{2}p_{2}right).}

В начале интервала времени Delta t объем жидкости, заключённый между двумя поверхностями A_{1} и A_{2}, состоит из левого голубого элемента и средней синей части, в конце этого интервала сместившийся объём состоит из средней синей части и правого голубого элемента. Так как течение стационарное, вклад синего фрагмента в энергию и массу обсуждаемого объёма жидкости не меняется, а сохранение массы позволяет заключить, что масса левого голубого элемента равна массе правого голубого элемента: {displaystyle Delta m=Delta tv_{1}A_{1}rho _{1}=Delta tv_{2}A_{2}rho _{2}.} Поэтому работа сил, выражение для которой можно преобразовать к виду: {displaystyle Delta W=Delta mleft({frac {p_{1}}{rho _{1}}}-{frac {p_{2}}{rho _{2}}}right),} равна изменению энергии, равному, в свою очередь, разности энергий правого голубого элемента {displaystyle Delta E_{2}} и левого голубого элемента {displaystyle Delta E_{1}}.

Для несжимаемой жидкости можно, во-первых, в выражении для работы положить {displaystyle rho _{1}=rho _{2}=rho } и, во-вторых, в выражении для энергии элемента жидкости ограничиться кинетической и потенциальной энергией: {displaystyle Delta E_{1}=Delta mleft({frac {v_{1}^{2}}{2}}+gh_{1}right),} {displaystyle Delta E_{2}=Delta mleft({frac {v_{2}^{2}}{2}}+gh_{2}right).} После этого равенство {displaystyle Delta W=Delta E_{2}-Delta E_{1}} даёт: {displaystyle p_{1}+rho gh_{1}+{frac {rho v_{1}^{2}}{2}}=p_{2}+rho gh_{2}+{frac {rho v_{2}^{2}}{2}}}, или {displaystyle p+rho gh+{frac {rho v^{2}}{2}}={rm {const}}}.

Константа в правой части (может различаться для различных линий тока) иногда называется полным давлением[2]. Могут также использоваться термины «весовое давление» rho gh, «статическое давление» p и «динамическое давление» {displaystyle rho v^{2}/2}. По словам Д. В. Сивухина[13], нерациональность этих понятий отмечалась многими физиками.

Размерность всех слагаемых — единица энергии на единицу объёма. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Третье слагаемое по своему происхождению является работой сил давления (см. приведённый выше вывод уравнения Бернулли), но в гидравлике может называться «энергией давления» и частью потенциальной энергии[14]).

Вывод формулы Торричелли из закона Бернулли[править | править код]

Иллюстрация формулы Торричелли

В применении к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда закон Бернулли даёт равенство полных давлений на свободной поверхности жидкости и на выходе из отверстия:

{displaystyle rho gh+p_{0}={frac {rho v^{2}}{2}}+p_{0},}

где

h — высота столба жидкости в сосуде, отсчитанная от уровня отверстия,
v — скорость истечения жидкости,
p_{0} — атмосферное давление.

Отсюда: v={sqrt {2gh}}. Это — формула Торричелли. Она показывает, что при истечении жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты h. Или, если истекающую из малого отверстия в сосуде струю направить вверх, в верхней точке (в пренебрежении потерями) струя достигнет уровня свободной поверхности в сосуде[15].

Другие проявления и применения закона Бернулли[править | править код]

Закон Бернулли объясняет эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем в широкой части

Приближение несжимаемой жидкости, а с ним и закон Бернулли справедливы и для ламинарных течений газа, если только скорости течения малы по сравнению со скоростью звука[16].

Вдоль горизонтальной трубы координата z постоянна и уравнение Бернулли принимает вид {displaystyle {frac {rho v^{2}}{2}}+p={text{const}}}. Отсюда следует, что при уменьшении сечения потока из-за возрастания скорости давление падает. Эффект понижения давления при увеличении скорости потока лежит в основе работы расходомера Вентури[17] и струйного насоса[1].

Закон Бернулли объясняет, почему суда, движущиеся параллельным курсом, могут притягиваться друг к другу (например, такой инцидент произошёл с лайнером «Олимпик»)[18].

Применение в гидравлике[править | править код]

Последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики. Для технических приложений часто уравнение Бернулли записывается в виде, в котором все члены разделены на «удельный вес» {displaystyle rho g}:

{displaystyle H=h+{frac {p}{rho g}}+{frac {v^{2}}{2g}}={text{const}},}

где имеющие размерность длины члены в этом уравнении могут иметь следующие названия:

Напор[19]
Размерность L
Единицы измерения
СИ метр
Примечания
Полное давление, делённое на удельный вес.
H — гидравлическая высота[4] или напор[19],
h — нивелирная высота[4],
{displaystyle {frac {p}{rho g}}} — пьезометрическая высота[4] или (в сумме с нивелирной высотой) гидростатический напор[19],
{displaystyle {frac {v^{2}}{2g}}} — скоростная высота[4] или скоростной напор[19].

Закон Бернулли справедлив только для идеальных жидкостей, в которых отсутствуют потери на вязкое трение. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, приближённо учитывающих различные «гидравлические потери напора»[19].

Интеграл Бернулли в баротропных течениях[править | править код]

Уравнение Бернулли может быть выведено и из уравнения движения жидкости[K 2][K 3]. При этом течение предполагается стационарным и баротропным. Последнее означает, что плотность жидкости или газа не обязательно постоянна (как у предполагавшейся ранее несжимаемой жидкости), но является функцией только давления: {displaystyle rho =rho (p)}, что позволяет ввести функцию давления[22] {displaystyle {mathcal {P}}=int {frac {mathrm {d} p}{rho (p)}}.} В этих предположениях величина

{displaystyle {frac {v^{2}}{2}}+gh+{mathcal {P}}={text{const}}}

постоянна вдоль любой линии тока и любой вихревой линии. Соотношение справедливо для течения в любом потенциальном поле, при этом gh заменяется на потенциал массовой силы varphi .

Вывод интеграла Бернулли для баротропного течения

Для безвихревых баротропных течений, скорость которых может быть выражена в виде градиента потенциала скорости {displaystyle {vec {v}}=operatorname {grad} psi }, интеграл Бернулли в виде {displaystyle {frac {partial psi }{partial t}}+{frac {left(operatorname {grad} psi right)^{2}}{2}}+gh+{cal {P}}=mathrm {const} }[K 4] сохраняется также в нестационарных течениях, причём постоянная в правой части имеет одинаковое значение для всего течения[25].

Формула Сен-Венана — Ванцеля[править | править код]

Если в течении совершенного газа выполняется адиабатический закон[26]

{displaystyle p={frac {p_{0}}{rho _{0}^{gamma }}}rho ^{gamma },qquad rho ={frac {rho _{0}}{p_{0}^{1/gamma }}}p^{1/gamma },qquad {cal {P}}=-{frac {gamma }{gamma -1}}{frac {p_{0}}{rho _{0}}}left[1-left({frac {p}{p_{0}}}right)^{(gamma -1)/gamma }right],}

то уравнение Бернулли выражается так[27] (вкладом от силы тяжести обычно можно пренебречь):

{displaystyle {frac {v^{2}}{2}}-{frac {gamma }{gamma -1}}{frac {p_{0}}{rho _{0}}}left[1-left({frac {p}{p_{0}}}right)^{(gamma -1)/gamma }right]=mathrm {const} } вдоль линии тока или вихревой линии. Здесь
gamma ={frac {C_{p}}{C_{V}}} — показатель адиабаты газа, выражающийся через теплоёмкости при постоянном давлении и при постоянном объёме,
{displaystyle p, rho } — давление и плотность газа,
{displaystyle p_{0}, rho _{0}} — условно выбранные постоянные (одинаковые для всего течения) значения давления и плотности.

С помощью полученной формулы находят скорость газа, вытекающего из сосуда с высоким давлением через малое отверстие. Удобно давление и плотность газа в сосуде, скорость газа в котором равна нулю, принять за {displaystyle p_{0}, rho _{0},} тогда скорость истечения выражается через внешнее давление p по формуле Сен-Венана — Ванцеля[28]:

{displaystyle v^{2}={frac {2gamma }{gamma -1}}{frac {p_{0}}{rho _{0}}}left[1-left({frac {p}{p_{0}}}right)^{(gamma -1)/gamma }right].}

Термодинамика закона Бернулли[править | править код]

Из термодинамики следует, что вдоль линии тока любого стационарного течения идеальной жидкости

{displaystyle {frac {v^{2}}{2}}+w+varphi ={text{const}},quad s={text{const}},}

где w — энтальпия единицы массы, varphi  — гравитационный потенциал (равный {displaystyle gz} для однородной силы тяжести), s — энтропия единицы массы.

Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений

Интеграл Бернулли применяют в инженерных расчётах, в том числе для сред, весьма далёких по своим свойствам от идеального газа, например для водяного пара, используемого в качестве теплоносителя в паровых турбинах. При этом могут использоваться так называемые диаграммы Молье, представляющие удельную энтальпию (по оси ординат) как функцию удельной энтропии (по оси абсцисс), и, например, давления (или температуры) в виде семейства изобар (изотерм). В этом случае последовательность состояний вдоль линии тока лежит на некоторой вертикальной линии ({displaystyle s={text{const}}}). Длина отрезка этой линии, отсекаемого двумя изобарами, соответствующими начальному и конечному давлению теплоносителя, равна половине изменения квадрата скорости[31].

Обобщения интеграла Бернулли[править | править код]

Интеграл Бернулли также сохраняется при переходе потока через фронт ударной волны, в системе отсчета, в которой ударная волна покоится[32]. Однако при таком переходе энтропия среды не остаётся постоянной (возрастает), поэтому соотношение Бернулли является лишь одним из трёх соотношений Гюгонио, наряду с законами сохранения массы и импульса, связывающих состояние среды за фронтом с состоянием среды перед фронтом и со скоростью ударной волны.

Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений[33]), в магнитной гидродинамике[34], феррогидродинамике[35]. В релятивистской гидродинамике, когда скорости течения становятся сравнимыми со скоростью света c, интеграл формулируется в терминах релятивистски инвариантных[36] удельной энтальпии и удельной энтропии[37].

Комментарии[править | править код]

  1. ↑ В записи Д.Бернулли в явном виде не фигурировало внутреннее давление в жидкости[8][9][10].
  2. ↑ «…[Вывод теоремы Бернулли из уравнения энергии] обедняет содержание теоремы Бернулли … Интеграл Бернулли, вообще говоря, не зависит от уравнения энергии, хотя действительно совпадает с ним для изоэнтропического и адиабатического движения совершенного газа»[20].
  3. ↑ «Два … пути получения уравнения Бернулли не эквивалентны. При энергетическом выводе нет необходимости в предположении об изэнтропичности течения. При интегрировании уравнения движения интегралы Бернулли получаются не только вдоль линий тока, но и вдоль вихревых линий»[21].
  4. ↑ В русскоязычной литературе интеграл Бернулли для потенциальных течений несжимаемой или баротропной жидкости известен как интеграл Коши — Лагранжа[25]

Примечания[править | править код]

  1. ↑ 1 2 Ландсберг Г. С. Закон Бернулли, 1985.
  2. ↑ 1 2 3 4 Вишневецкий С. Л. Бернулли уравнение, 1988.
  3. ↑ Титьенс О., Прандтль Л. Гидро- и аэромеханика, 1933.
  4. ↑ 1 2 3 4 5 Лойцянский Л. Г. Механика жидкости и газа, 2003, §24. Теорема Бернулли.
  5. ↑ Милн-Томсон Л. М. Теоретическая гидродинамика, 1964.
  6. ↑ Седов Л. И. Механика сплошной среды, 1970.
  7. ↑ Чёрный Г. Г. Газовая динамика, 1988.
  8. ↑ Трусделл К. Очерки по истории механики, 2002.
  9. ↑ Михайлов Г. К., 1999, с. 17.
  10. ↑ Darrigol O. A history of hydrodynamics, 2005, с. 9.
  11. ↑ Трусделл К. Очерки по истории механики, 2002, с. 255, 257.
  12. ↑ Euler L. Continuation des recherches, 1755 (1757), с. 331.
  13. ↑ 1 2 Сивухин Д. В. Механика, 1989, §94. Стационарное движение идеальной жидкости. Уравнение Бернулли.
  14. ↑ Чугаев Р. Р. Гидравлика. — Л.: Энергия, 1975. — 600 с.
  15. ↑ Сивухин Д. В. Механика, 1989, §95. Примеры на применение уравнения Бернулли. Формула Торричелли.
  16. ↑ Сивухин Д. В. Механика, 1989, §94, формула (94.6).
  17. ↑ Молоканов Ю. К. Процессы и аппараты нефтегазопереработки. — М.: Химия, 1980. — С. 60. — 408 с.
  18. ↑ Я. И. Перельман. Отчего притягиваются корабли? Дата обращения: 27 декабря 2018. Архивировано 11 мая 2012 года.
  19. ↑ 1 2 3 4 5 Напор, 1992.
  20. ↑ Бэтчелор Дж. Введение в динамику жидкости, 1973, Примечание Г. Ю. Степанова, с. 208.
  21. ↑ Гольдштейн Р. В., Городцов В. А. Механика сплошных сред, 2000, с. 104.
  22. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (9).
  23. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §23, уравнение (7).
  24. ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VIII. §2, уравнение (2.1).
  25. ↑ 1 2 Лойцянский Л. Г. Механика жидкости и газа, 2003, §42. Интеграл Лагранжа — Коши.
  26. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (29).
  27. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (30).
  28. ↑ Лойцянский Л. Г. Механика жидкости и газа, 2003, §24, уравнение (31).
  29. ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (2.4).
  30. ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VII. §2. Функция давления.
  31. ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 446.
  32. ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, §85.
  33. ↑ Голубкин В. Н., Сизых Г. Б. О некоторых общих свойствах плоскопараллельных течений вязкой жидкости // Известия АН СССР, серия Механика жидкости и газа : журнал. — 1987. — № 3. — С. 176–178. — doi:10.1007/BF01051932.
  34. ↑ Куликовский А. Г., Любимов Г. А. Магнитная гидродинамика. — М.: Физматлит, 1962. — С. 54. — 248 с.
  35. ↑ Розенцвейг Р. Феррогидродинамика / Пер. с англ. под ред. В. В. Гогосова. — М.: Мир, 1989. — С. 136. — 359 с. — ISBN 5-03-000997-3.
  36. ↑ Зубарев Д. Н., Релятивистская термодинамика, 1994.
  37. ↑ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2001, Уравнение (134.11).

Литература[править | править код]

  • Бэтчелор Дж. Введение в динамику жидкости / Пер. с англ. под ред. Г. Ю. Степанова. — М.: Мир, 1973. — 760 с.
  • Вишневецкий С. Л. Бернулли уравнение // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова-Бома эффект — Длинные линии. — С. 187. — 704 с.
  • Гольдштейн Р. В., Городцов В. А. Механика сплошных сред. Часть 1. — М.: Физматлит, 2000. — 256 с. — ISBN 5-02-015555-1.
  • Зубарев, Д. Н. Релятивистская термодинамика // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 333—334. — 704 с. — ISBN 5-85270-087-8.
  • Ландау Л. Д., Лифшиц Е. М. Гидродинамика. — Издание 5-е, стереотипное. — М.: Физматлит, 2001. — 736 с. — («Теоретическая физика», том VI). — ISBN 5-9221-0121-8.
  • Лойцянский Л. Г. Механика жидкости и газа. — М.: Дрофа, 2003. — 842 с. — ISBN 5-7107-6327-6.
  • Милн-Томсон Л. М. Теоретическая гидродинамика. — М.: Мир, 1964. — 656 с.
  • Михайлов Г. К. Становление гидравлики и гидродинамики в трудах петербургских академиков (XVIII) // Известия Академии наук, серия Механика жидкости и газа : журнал. — 1999. — Вып. 6. — С. 7–25.
  • Напор // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный компрессор — Пойнтинга теорема. — С. 242. — 672 с. — ISBN 5-85270-019-3.
  • Поль Р. В. Механика, акустика и учение о теплоте. — Рипол Классик, 2013. — 490 с. — ISBN 5458431251, 9785458431255.
  • Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — 568 с.
  • Сивухин Д. В. Общий курс физики. — Издание 3-е, исправленное и дополненное. — М.: Наука, 1989. — Т. I. Механика. — 576 с. — ISBN 5-02-014054-6.
  • Титьенс О., Прандтль Л. Гидро- и аэромеханика. — М.–Л.: ГТТИ, 1933. — Т. 1. — 224 с.
  • Трусделл К. Очерки по истории механики. — М. — Ижевск: Институт компьютерных исследований, 2002. — 316 с. — ISBN 5-93972-192-3.
  • Фабер Т. Е. Гидроаэродинамика / Пер. с англ. под ред. А. А. Павельева. — М.: Постмаркет, 2001. — 560 с. — ISBN 5-901095-04-9.
  • Чёрный Г. Г. Газовая динамика. — М.: Наука, 1988. — 424 с. — ISBN 5-02-013814-2.
  • §182. Закон Бернулли // Элементарный учебник физики / Под ред. Г. С. Ландсберга. — М.: Наука, 1985. — Т. 1. Механика. Теплота. Молекулярная физика.
  • Darrigol O. Worlds of flow. A history of hydrodynamics from the Bernoullis to Prandtl. — Oxford: Oxford University Press, 2005. — 356 с. — ISBN 978-0-19-856843-8.
  • Euler L. Continuation des recherches sur la théorie du mouvement des fluides // Mémoires de l’Académie royale des sciences et belles lettres. — Berlin, 1755 (1757). — Т. 11. — С. 316—361.
  • Truesdell, Clifford Ambrose. Rational fluid mechanics, 1687–1765. Editor’s introduction to Euleri Opera omnia II 12 // Leonardi Euleri. Opera Omnia. — Lausanne: Auctoritate et Impensis, Societas Scientiarum Naturalium Helveticae, 1954. — Т. 12. — С. I—CXXV. — (II).

Ссылки[править | править код]

  • Русский перевод трактата Даниила Бернулли, в котором впервые появляется интеграл (закон) Бернулли
Источник

Как узнать скорость потока воды в трубе зная давление, диаметр, расход и плотность?

Физика, космос, планеты, астрономия, космонавтика  · 13 февр 2022

Задача на уровне 9-10 класса. У нас есть давление P, диаметр d, расход A, плотность ρ. Необходимо найти скорость потока U. Специально обозначаю скорость непривычной буквой U, чтобы не перепутать с объёмом V.

Скорость U – это длина l в единицу времени: U=I/t.

Расход A – это объём V в единицу времени: A=V/t.

Объем V – это площадь поперечного сечения S, помноженная на длину l: V=S*l. Площадь S = П*d^2 / 4.

Подставляем всё в формулу А.

Для вычисления скорости U достаточно расхода А и диаметра d. Остальные величины не понадобятся.

991

Тоесть скорость никак не зависит от давления? Но ведь закон Бернулли говорит обратное. Мне нужна конкретная привязка к давлению.

Комментировать ответ…Комментировать…

О сообществе

Источник



Ученик

(99),
закрыт



3 года назад

Fizeg

Гуру

(4496)


12 лет назад

Думаю, можно так попробовать:

p – давление в Па (1атм=10^5Па)
“ро” – плотность воды (1000 Кг/м^3)
v – скорость (получается 14м/с)
Это если труба горизонтальная, и вода движется за счет того давления.

Kevin Kurt

Профи

(966)


12 лет назад

Пример:
труба 150 мм, с одной стороны насос с другой закрытая задвижка длина трубы 5000 метров (5 Км) . давление в трубе 1 атм. скорость потока воды естественно нулевая.
даже с открытой задвижкой поток в трубе 5 километров и трубе 5 метров при одинаковых начальных условиях будет разным.
и, на закуску, обычно значение имеет не скорость потока, а объем проходящий через поперечное сечение – расход воды, измеряемый в метрах кубических за секунду (минуту, час, сутки, год).

Источник

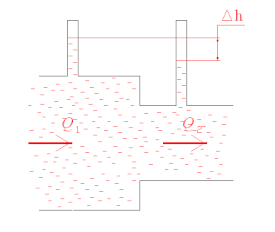
Связь давления и скорости в потоке

Связь давления и
скорости в потоке жидкости —
обратная: если в каком-то месте потока
скорость увеличивается, то давление
здесь малó,
и, наоборот, там, где скорости невелики,
давление повышенное. Эту законо­мерность
объясним на основе уравнения Бернýлли.

Рассмотрим работу
водоструйного насоса (см. рис. 11). На
подходе по на­гнетательному трубопроводу
1 поток рабочей жидкости имеет
относи­те­ль­но небольшую скорость
v1
и высокое избыточное давление pизб1.
Проходя через соплó
2, поток сужается, скорость его резко
возрастает до v2.
Для дальнейших рассуждений запишем
уравнение Бернýлли
так:

.

Здесь нет z1
и z2,
так как труба горизонтальная, а величиной
потерь на­пора DH»
0
пренебрегаем. Так как в правой части
уравнения кинети­ческая составляющая
энергии потока резко возросла из-за
увеличения v2,
то потенциальная составляющая, связанная
с избыточным давлением после соплá
pизб2,
наоборот, уменьшится. Величину pизб2
можно выразить из этого уравнения и
найти численное значение. Если pизб2
получается отри­цательным, то, значит,
возник вакуум (полное давление в струе
стало меньше атмосферного). В последнем
случае пьезометрическая линия опу­стится
ниже отметки самой струи (см. рис 11).

Таким образом в струе
рабочей жидкости после соплá
образуется об­ласть пониженного
давления или даже вакуум, что вызывает
подсос транс­портируемой жид­кости
по всасывающему трубопроводу 3 (см. рис.
11). Далее обе жидкости смешиваются в
горловине 4 и транспортируются по
отво­дяще­му трубопро­воду 5.

Водоструйные насосы
не имеют трущихся частей, в этом их
пре­имущес­тво перед механическими.
По их принципу работают также эжекто­ры,
гидро­эле­ваторы, насосы для создания
вакуума.

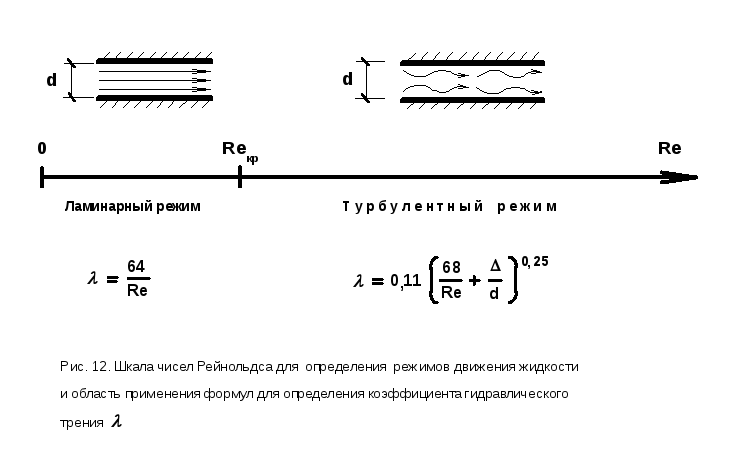
Режимы движения жидкости

При проведении
гидравлического расчёта в первую очередь
нужно выяснять: какой режим движения
будет наблюдаться у данного потока?

Режимы движения всех
потоков (напорных и безнапорных) де­лятся
на два типа (рис. 12):

1) ламинарный, то есть
спокойный, параллельноструйный, при
ма­лых скоростях;

2) турбулентный, то
есть бурлящий, вихреобразный, с
водоворота­ми, при больших скоростях.

Для выяснения типа
режима нужно рассчитать число Рейнольдса
Re
и сравнить его с критическим Reкр.

Число Рéйнольдса
Re
—
это безразмерный критерий, вычисляемый
по формулам:

— для напорных
потоков

Re
=vd/n
,

где d
—
внутренний диаметр напорного трубопровода;

— для безнапорных
потоков

Re
=vR/n,

где R
—
гидравлический радиус безнапорного
потока, м
(см. с. 14).

Критическое число
Рейнольдса Reкр
—
это число Рейнольдса, при котором
наступает смена режима движения.

Для напорных потоков

Reкр=2320,

для безнапорных
потоков

Reкр
»
500.

Упрощённо режим
движения потока можно определить по
шкале чисел Рейнольдса (см. рис. 12).
Рассмотрим пример с напорной водопроводной
тру­бой, у которой d=20
мм, v=1
м/с, n
=10–6
м2/с.
Для потока в дан­ной трубе число
Рейнольдса составит:

Re=1×0,02/10–6
=
20000.

Число 20000
больше, чем
Reкр=2320
(для напорных
потоков) и на рис.12 оно находится в правой
части шкалы, следовательно, режим потока
турбулентный и все дальнейшие
гидравлические расчёты должны проводиться
только по зависимостям и формулам для
этого ре­жима.

Источник

Принцип Бернулли заложил основы знания о движении жидкости, которое впоследствии перешло в самостоятельную науку — гидродинамику.

Физическая сущность закона Бернулли

Швейцарский математик и физик Даниил Бернулли родился в 1716 году в Голландии. За свою научную карьеру он получил звания Почетного члена Берлинской, Петербургской и Парижской академии наук, являлся членом Лондонского королевского общества. Главным научным трудом ученого является работа «Гидродинамика, или изъяснение сил и движений жидкости», опубликованная в 1733 году. Именно в этой книге были описаны физические основы механики жидкости.

Закон, названный его именем, Бернулли сформулировал во время работы в России, изучая взаимосвязь давления жидкости с ее скоростью. В математическом выражении он определяется уравнением Бернулли. Давайте разберемся, в чем состоит сущность закона.

Для начала определим, что закон Бернулли рассматривает движение потока несжимаемой идеальной жидкости, на которую действуют только силы тяжести и силы упругости.

Идеальная жидкость — это жидкость, в которой полностью отсутствует внутреннее трение и теплопроводность, ввиду чего, она лишена касательных напряжений между соседними слоями.

Подобная идеализация применяется при рассмотрении течения в гидродинамике. В законе Бернулли рассматривается стационарное течение жидкости — это движение слоев жидкости относительно друг друга и относительно ее самой, при котором скорость потока в некой конкретной точке не меняется, сохраняя свое постоянное значение. Давление при стационарном течении идеальной жидкости одинаково во всех поперечных сечениях трубки тока.

Для наглядности рассмотрим стационарное течение идеальной жидкости по трубе переменного сечения. В одном месте сечение этой трубки равно S1, а в другом — S2. При стационарном потоке через все сечения за определенный промежуток времени пройдет одинаковый объем жидкости, так как в ином случае, невозможность сжатия привела бы к ее разрыву. Таким образом, мы получаем уравнение неразрывности струи, определяющее соотношение между скоростью течения (v) и площадью сечения (S): S1v1=S2v2

Бутылка

Источник: getclass.ru

При этом давление в сечении S1 меньше, чем в сечении S2. Как вы думаете, в каком из сечений скорость течения жидкости будет больше? Казалось бы, что по логике, скорость должна увеличиваться в том месте, где больше давление. Однако, согласно закону Бернулли, скорость увеличивается с уменьшением площади сечения. В этом-то и состоит парадоксальность принципа.

Закон Бернулли гласит, в тех участках течения жидкости или газа, где скорость больше, давление меньше, и наоборот, с увеличением давления жидкости, протекающей в трубе, скорость ее движения уменьшается. То есть, где больше скорость (v), там меньше давление (p).

Чтобы убедиться в этом, достаточно провести небольшой опыт из подручных средств. Возьмите два шара одного размера и подвесьте их так, чтобы между ними сохранялось небольшое расстояние. Подуйте между шарами или пустите воздух из фена. Шары вместо того, чтобы отдалиться, притянутся друг к другу. Это прямое следствие описанного закона, так как в том месте, куда вы дули, давление стало уменьшаться, а скорость шаров возросла, приблизив их друг к другу.

Закон Бернулли

Источник: getclass.ru

Закон Бернулли как следствие закона сохранения энергии

Из уравнения неразрывности следует, что в идеальной жидкости сумма статистического и динамического давлений и скоростного напора постоянна в любом сечении вдоль трубы. Являясь следствием закона сохранения, вывод уравнение Бернулли для элементарной струйки жидкости выглядит так:

(tfrac{rho v^2}{2} + rho g h + p = mathrm{const}),

где (~rho) — плотность жидкости, (~v) — скорость потока, (~h) — высота, на которой находится рассматриваемый элемент жидкости, (~p) — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, (~g) — ускорение свободного падения.

При этом давление P — это статическое давление, которое получается в результате взаимодействия соседних слоев жидкости. Величина ρv2/2 — это динамическое давление, обусловленное движением жидкости, а ρgh — это давление, образованное массой вертикального столба жидкости высотой h, создаваемое силой тяжести.

Все эти величины имеют специальные обозначения, где h — высота положения или геометрический напор, P / ρ∙g — пьезометрический напор, v2 / 2g — скоростной напор.

Сумма трех слагаемых уравнения называется полным напором (H), то есть для идеальной жидкости при стационарном течении сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.

Для трубы, расположенной горизонтально, где величина высоты остается неизменной, уравнение Бернулли упрощается и выглядит так:

({textstylefrac{rho v^2}2}+p=mathrm{const})

Проявление закона Бернулли в жизни

Закон Бернулли описывает одно из основных свойств гидравлики. Эффект, описанный швейцарским ученым, широко проявляется в природе и быту. Также широко его применение в технике. На основе принципа Бернулли работают такие приборы, как пульверизатор, водоструйный насос, аэрограф.

Чтобы понять механизм устройства, рассмотрим строение пульверизатора, которое включает в себя вертикальную трубку и горизонтальное сопло. Вертикальную трубку опускают в жидкость, в то время как по соплу пропускают воздух. Атмосферное давление, которое больше давления в струе воздуха, заставляет жидкость подниматься по трубке. Следовательно, при попадании в струю воздуха, происходит распределение жидкости.

Пульверизатор

Источник: dststone.ru

В повседневной жизни закон Бернулли можно наблюдать, сидя у камина. При сильном ветре скорость воздушного потока возрастает, и, соответственно, падает давление. И так как давление воздуха в комнате выше, пламя, уходит вверх по дымоходу.

Это свойство используется и в аэродинамике для объяснения того, как возникает подъемная сила самолета или другого летательного аппарата, которое тяжелее воздуха.

В истории имеются и случаи отрицательного проявления закона. В 1912 году произошло столкновение океанского парохода «Олимпик» с гораздо меньшим по масштабам крейсером «Гаук», который плыл параллельно пароходу на расстоянии около 100 метров. Вдруг «Гаук» резко двинулся прямо на «Олимпик» и протаранил его силой удара. Так как два корабля были друг к другу слишком близко, скорость воды между ними стала больше, чем с другой стороны, вызвав дополнительную силу. Следовательно, вместо того, чтобы отдалиться, корабли притянулись друг к другу, что и стало причиной катастрофы.

Корабли

Источник: wikipedia.org

В природе закон Бернулли проявляется во время урагана, когда из-за сильного ветра с домов слетают крыши. Это происходит, потому что скорость, с которой движется воздух вверху, очень большая, тогда как на чердаке она равна нулю. Как вы уже узнаете, там, где скорость потока больше, давление меньше, а там, где скорость меньше, давление больше. В результате образовавшейся разности давлений ураган и срывает кровлю.

Существует еще большое количество интересных примеров, изучение которых во многом упрощает усвоение закона Бернулли. Если вам нужно определить проявление закона в каком-то конкретном явление, обращайтесь к специалистам сервиса Феникс.Хелп, которые помогут решить задачу любой сложности.

Источник

Добавить комментарий