Важнейшими характеристиками потоков жидкости или газа (например при движении их в трубах) являются объемный расход и скорость потока.
Объем жидкости, проходящей через заданную площадь за единицу времени. Измеряется в системе СИ в кубических метрах в секунду (м3/с). Обычно обозначается символом QQ.
Скорость движения жидкости, которая численно равна отношению расхода жидкости Q к площади живого сечения.
Понятие расхода
Если через заданную площадь SS жидкость протекает с равномерно распределенной по площади скоростью VV под углом θθ к направлению скорости до перпендикуляра площади SS, то расход составит:
Q=V⋅S⋅cosθQ = V ⋅ S ⋅ cosθ
В частном случае, когда скорость потока перпендикулярна к площади SS, уравнение примет вид:
Q=V⋅SQ = V ⋅ S
Общий случай
Записанные выше уравнения обычно называют уравнениями непрерывности (для одномерных течений несжимаемой жидкости). Если скорость жидкости через заданную площадь неодинакова (или, если область не является плоской), то объемный расход потока жидкости может быть рассчитан с помощью интеграла по площади:
Q=∬Su⋅dωQ = ∬S u ⋅ dω,
где dωdω дифференциал поверхности, который записывается как:
dω=ndSdω = n dS,
где nn – единичный вектор нормали к поверхности; dSdS – дифференциал площади SS.
Полученное уравнение потока вектора скорости через поверхность SS является скалярной величиной. Физически поток вектора скорости представляет собой секундный объемный расход жидкости через поверхность SS.
Измерение скорости потока
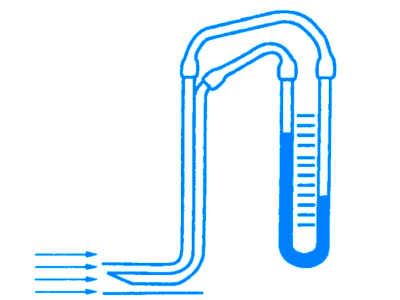
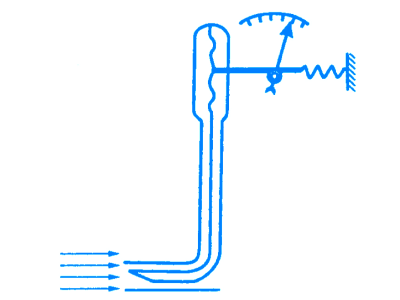
Для измерения скорости потока жидкости или газа используется прибор, предложенный французским ученым А. Пито (1695-1771). Этот прибор имеет две трубки: одну с отверстием напротив потока и вторую с отверстием, параллельным потоку:
Трубки соединены с дифференциальным манометром:
В отверстии первой трубки скорость жидкости или газа равна нулю, а в отверстии второй скорость потока сохраняется. Применив уравнение Бернулли для частиц потока в отверстиях трубок, получим:
p1=ρv22+p2{{p}_{1}}=frac{rho {{v}^{2}}}{2}+{{p}_{2}}
Составляющую ρv2/2ρv^2/2, имеющую размерность давления, называют динамическим давлениям, а составляющую р2р^2 – статичным.
Из уравнения определим скорость потока:
v=2(p1−p2)ρv=sqrt{frac{2({{p}_{1}}-{{p}_{2}})}{rho }}
Здесь ρρ – плотность вещества в потоке; (р1р_1 – р2р_2) находят по разнице высот жидкости в манометре. Согласно данной формуле можно проградуировать манометр в трубке Пито для измерения скорости потока.
Трубку Пито используют для измерения скорости кораблей и самолетов.
Скорость истечения жидкости из бака
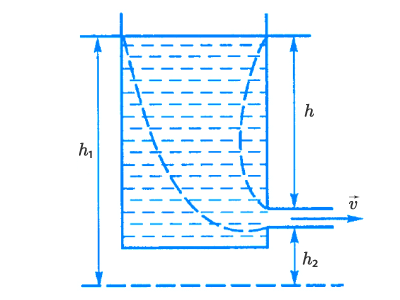
Найдем скорость истечения жидкости из бака:
Для этого выделим в жидкости трубку потока (показанную штриховой линией) и применим к ее сечениям (взятых на поверхности жидкости в баке, и в отверстии утечки) уравнение Бернулли. Если при этом учесть, что давления в обоих сечениях одинаковы и равны атмосферному, а скорость в сечении на поверхности жидкости в баке приравнять к нулю, то получим:
ρgh1=ρv22+ρgh2rho g{{h}_{1}}=frac{rho {{v}^{2}}}{2}+rho g{{h}_{2}}
Отсюда находим vv – скорость истечения жидкости из бака:
v=2g(h1−h2)v=sqrt{2g({{h}_{1}}-{{h}_{2}})}
Поскольку h1−h2=hh_1 – h_2 = h – высота уровня жидкости в баке над отверстием истечения, окончательно:
v=2ghv=sqrt{2gh}
Эту формулу вывел итальянский ученый Э. Торричелли (1608-1647) в 1641 Из нее следует, что скорость истечения жидкости (идеальной) из сосуда такова, какова была бы скорость приобретенная телом, свободно падая с высоты hh.
Цилиндрический сосуд высотой hh = 70 см с площадью дна SS = 600 см2 заполнено водой. В дне сосуда образовалось отверстие S1S_1 = 1 см2. За какое время вытечет вода из сосуда?
Приняв во внимание, что скорость истечения воды из сосуда со временем меняется, поскольку меняется уровень воды, определим сначала ее объем утечки за время dtdt:
dV=S1vdtdV = S_1vdt
где v=2ghv=sqrt{2gh} (hh – уровень воды в заданный момент времени); поэтому:
dV=S12ghdtdV={{S}_{1}}sqrt{2gh}dt
Этот объем утечки можно выразить через снижение уровня воды:
dV=−SdhdV = -Sdh
Если приравнять выражения и разделить переменные, то получим дифференциальное уравнение:
dhh=−S1S2gdtfrac{dh}{sqrt{h}}=-frac{{{S}_{1}}}{S}sqrt{2g}dt
Интегрируя обе части этого уравнения, получаем:
2h=−S1S2gdt+C2sqrt{h}=-frac{{{S}_{1}}}{S}sqrt{2g}dt+C
Найдем постоянную интегрирования. Поскольку при tt = 0, h=h0h = h_0, получим:
Тогда равенство примет вид:
h0−h=S12g2Stsqrt{{{h}_{0}}}-sqrt{h}=frac{{{S}_{1}}sqrt{2g}}{2S}t
В случае полного вытекания воды (hh = 0) равенство примет вид:
t=2SS1h02gt=frac{2S}{{{S}_{1}}}sqrt{frac{{{h}_{0}}}{2g}}
Подставив значения из условия получим
tt = 227 с.
Тест по теме «Скорость потока»
Массовый расход — масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени. Измеряется в единицах массы за единицу времени, в системе единиц СИ выражается в килограммах за секунду (кг/с).
Понятие массового расхода используется для характеристики потоков таких сред, как: газы, жидкости, сыпучие вещества и газопылевые смеси.
Для расчёта массовых расходов используют значения средней скорости потока как усреднённой характеристики интенсивности протекания вещества. Средней скоростью потока в данном сечении называется такая одинаковая для всех точек сечения потока скорость движения вещества, при которой через это сечение проходит тот же расход, что и при действительном распределении скоростей движения вещества.
Массовый расход может быть вычислен через плотность вещества, площадь сечения потока и среднюю скорость потока в этом сечении:
Q = ρVS
где:
Q массовый расход, кг/с;
ρ — плотность вещества, кг/м³;
V — средняя скорость потока, м/с;
S — площадь сечения потока, м².
Формула может быть выражена через объёмный расход:
Q= ρQ’
где:
ρ — плотность вещества, кг/м³;
Q’— объёмный расход, м³/с.
———
Решение:
Дано: d-диаметр трубы (159мм=0,159м)
Q-массовый пасход. ( 10000кг/ч={10000/3600}кг/с =2,78 кг/с)
Найти V–cкорость потока (м/с)
ρ=плотность /видимо, имеется ввиду вода? /воды ( 1000кг/м^3)
Вычислим площадь сечения:
S=(πd^2)/4=(3,14*0,159^2)/4=0,02(м^2)
Вычислим скорость потока:
V=Q/(ρS)= 2,78/(1000*0,02)=0,136(м/с)
Ответ: Скорость потока равна 0, 136 метра в секунду.
Как узнать скорость потока воды в трубе зная давление, диаметр, расход и плотность?
Физика, космос, планеты, астрономия, космонавтика. Автор одноименного Дзен канала dzen.ru/… · 13 февр 2022
Задача на уровне 9-10 класса. У нас есть давление P, диаметр d, расход A, плотность ρ. Необходимо найти скорость потока U. Специально обозначаю скорость непривычной буквой U, чтобы не перепутать с объёмом V.
Скорость U – это длина l в единицу времени: U=I/t.
Расход A – это объём V в единицу времени: A=V/t.
Объем V – это площадь поперечного сечения S, помноженная на длину l: V=S*l. Площадь S = П*d^2 / 4.
Подставляем всё в формулу А.
Для вычисления скорости U достаточно расхода А и диаметра d. Остальные величины не понадобятся.
952
Тоесть скорость никак не зависит от давления? Но ведь закон Бернулли говорит обратное. Мне нужна конкретная привязка к давлению.
Комментировать ответ…Комментировать…
О сообществе
Через уравнение.
S – пройденный путь, растояние, которое прошла, например, лодка. (км)
t – время, за которое она прошла расстояние S. (часов, минут)
V – собственная её скорость (км/ч, м/ч)
Такие задачи решаются далее: если известны: (под формулы подставляем числа)
t и V, то перемножаем – t * V, получаем S.
t и S, то расстояние делим время – S : t, получаем V
S и V, также – S : V, получаем t
Также если в задаче указана V (её ищем)
по течению, то V собственная + V по течению
против течения, то V собств. – V прот. теч.
Тогда формулы звучат так: если известны:
t и V, то t * (V с. +/- V) = S
t и S, то S : t = V с. +/- V
V и S, то S : (V c. +/- V) = t
Теперь ещё раз:
V c. – собственная скорость
V c. + V – скорость + скорость по теч.
V c. – V – скорость + скорость прот. теч.
Ну так чтоли… Плохой из меня учитель(((
Диаметр трубопроводов, скорость течения и расход теплоносителя.
В системе водяного отопления особенно часто у многих встает вопрос: Как вычислить диаметр трубопровода, по которому будет бежать теплоноситель (вода).
Данный материал предназначен понять, что такое диаметр, расход и скорость течения. И какие связи между ними. В других материалах будет подробный расчет диаметра для отопления.
Для того чтобы вычислить диаметр необходимо знать:
1. Расход теплоносителя (воды) в трубе.
2. Сопротивление движению теплоносителя (воды) в трубе определенной длины.
Вот необходимые формулы, которые нужно знать:

S-Площадь сечения м2 внутреннего просвета трубы
π-3,14-константа - отношение длины окружности к ее диаметру.
r-Радиус окружности, равный половине диаметра, м
Q-расход воды м3/с
D-Внутренний диаметр трубы, м
V-скорость течения теплоносителя, м/с
Сопротивление движению теплоносителя.
Любой движущийся внутри трубы теплоноситель, стремиться к тому, чтобы прекратить свое движение. Та сила, которая приложена к тому, чтобы остановить движение теплоносителя – является силой сопротивления.
Это сопротивление, называют – потерей напора. То есть движущийся теплоноситель по трубе определенной длины теряет напор.
Напор измеряется в метрах или в давлениях (Па). Для удобства в расчетах необходимо использовать метры.
Извиняйте, но я привык указывать потерю напора в метрах. 10 метров водного столба создают 0,1 МПа.
Для того, чтобы глубже понять смысл данного материла, рекомендую проследить за решением задачи.
Задача 1.
В трубе с внутренним диаметром 12 мм течет вода, со скоростью 1м/с. Найти расход.
Решение: Необходимо воспользоваться вышеуказанными формулами:
1. Находим сечение
2. Находим расход
Дано:
S=3.14•0,0122/4=0,000113 м2
Q=0,000113•1=0,000113 м3/с = 0,4 м3/ч.
Ответ: 0,4 м3/ч.
Задача 2.

Имеется насос, создающий постоянный расход 40 литров в минуту. К насосу подключена труба протяженностью 1 метр. Найти внутренний диаметр трубы при скорости движения воды 6 м/с.
Конечно, в реальности насосы не выдают постоянный расход и не выдают бесконечно большой напор. Поэтому по условию задачи мы условно приняли, что насос качает строго 40 литров в минуту, а напор насоса бесконечно большой. Ниже я поясню все нюансы подбора диаметра.
Решение.
Дано:
Q=40л/мин=0,000666666 м3/с
Из выше указанных формул получил такую формулу.

Ответ: 12мм
К сожалению, по такой формуле находить диаметр трубы не разумно и вот почему!
Каждый насос имеет вот такую расходно-сопротивляемую характеристику:

Это означает, что наш расход в конце трубы будет зависеть от потери напора, которое создается самой трубой.
Чем длиннее труба, тем больше потеря напора.
Чем меньше диаметр, тем больше потеря напора.
Чем выше скорость теплоносителя в трубе, тем больше потеря напора.
Углы, повороты, тройники, заужения и расширение трубы, тоже увеличивают потерю напора.
Такой характеристикой обладают на самом деле не насосы, а жидкости, которые подчиняются гидравлическим законам. Эти законы распространяются не только на насосы, но и на все трубы по которым течет жидкость. Даже если вода будет истекать из наполненного бака, там тоже будет присутствовать такая вот расходно-сопротивляемая характеристика.
Более детально потеря напора по длине трубопровода рассматривается в этой статье:
Потеря напора по длине трубопровода.
А теперь рассмотрим задачу из реального примера.
Хочу сразу Вас уведомить, что для следующей задачи были использованы эти материалы:
Профессиональный расчет диаметра трубы для водоснабжения.
Задача 2:

Стальная (железная) труба проложена длиной 376 метров с внутренним диаметром 100 мм, по длине трубы имеются 21 отводов (угловых поворотов 90°С). Труба проложена с перепадом 17м. То есть труба относительно горизонта идет вверх на высоту 17 метров. Характеристики насоса: Максимальный напор 50 метров (0,5МПа), максимальный расход 90м3/ч. Температура воды 16°С. Найти максимально возможный расход в конце трубы.
Дано:
D=100 мм = 0,1м
L=376м
Геометрическая высота=17м
Отводов 21 шт
Напор насоса= 0,5 МПа (50 метров водного столба)
Максимальный расход=90м3/ч
Температура воды 16°С.
Труба стальная железная
Найти максимальный расход = ?
Решение на видео:
Купить программу
Для решения необходимо знать график насосов: Зависимость расхода от напора.
Я выбрал визуально похожий график всех насосов, от реального может отличаться на 10-20%. Для более точного расчета необходим график насоса, который указан в паспорте насоса.

В нашем случае будет такой график:

Смотрите, прерывистой линией по горизонту обозначил 17 метров и на пересечение по кривой получаю максимально возможный расход: Qmax.
По графику я могу смело утверждать, что на перепаде высоты, мы теряем примерно: 14 м3/час. (90-Qmax=14 м3/ч).
Не существует прямой формулы, которая дает прямой расчет нахождения расхода, а если и существует, то она имеет ступенчатый характер и некоторую логику, которая способна Вас запутать – окончательно.
Ступенчатый расчет получается потому, что в формуле существует квадратичная особенность потерь напора в динамике (движение).
Поэтому решаем задачу ступенчато.
Поскольку мы имеем интервал расходов от 0 до 76 м3/час, то мне хочется проверить потерю напора при расходе равным: 45 м3/ч.
Находим скорость движения воды

Q=45 м3/ч = 0,0125 м3/сек.
V = (4•0,0125)/(3,14•0,1•0,1)=1,59 м/с
Находим число рейнольдса

ν=1,16•10-6=0,00000116. Взято из таблици. Для воды при температуре 16°С.
Re=(V•D)/ν=(1,59•0,1)/0,00000116=137069
Δэ=0,1мм=0,0001м. Взято из таблицы, для стальной (железной) трубы.
Далее сверяемся по таблице, где находим формулу по нахождению коэффициента гидравлического трения.
У меня попадает на вторую область при условии
10•D/Δэ < Re < 560•D/Δэ
10•0,1/0,0001 < Re < 560•0,1/0,0001
10 000 < Re < 560 000

λ=0,11( Δэ/D + 68/Re )0.25=0,11•( 0,0001/0,1 + 68/137069)0,25=0,0216
Далее завершаем формулой:
h=λ•(L•V2)/(D•2•g)= 0,0216•(376•1,59•1,59)/(0,1•2•9,81)=10,46 м.
Как видите, потеря составляет 10 метров. Далее определяем Q1, смотри график:

Теперь делаем оригинальный расчет при расходе равный 64м3/час
Q=64 м3/ч = 0,018 м3/сек.
V = (4•0,018)/(3,14•0,1•0,1)=2,29 м/с
Re=(V•D)/ν=(2,29•0,1)/0,00000116=197414
λ=0,11( Δэ/D + 68/Re )0.25=0,11•( 0,0001/0,1 + 68/197414)0,25=0,021
h=λ•(L•V2)/(D•2•g)= 0,021•(376•2,29 •2,29)/(0,1•2•9,81)=21,1 м.
Отмечаем на графике:
Qmax находится на пересечении кривой между Q1 и Q2 (Ровно середина кривой).

Ответ: Максимальный расход равен 54 м3/ч. Но это мы решили без сопротивления на поворотах.
Для проверки проверим:
Q=54 м3/ч = 0,015 м3/сек.
V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
Re=(V•D)/ν=(1,91•0,1)/0,00000116=164655
λ=0,11( Δэ/D + 68/Re )0.25=0,11•( 0,0001/0,1 + 68/164655)0,25=0,0213
h=λ•(L•V2)/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
Итог: Мы попали на Нпот=14,89=15м.
А теперь посчитаем сопротивление на поворотах:
Формула по нахождению напора на местном гидравлическом сопротивление:

Подробней об этом в разделе: Местные гидравлические сопротивления
h-потеря напора здесь она измеряется в метрах.
ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм.
V-скорость потока жидкости. Измеряется [Метр/секунда].
g-ускорение свободного падения равен 9,81 м/с2
ζ-Это коэффициент сопротивления. Для колена он равен примерно одному, если диаметр меньше 30мм. Для больших диаметров он уменьшается. Это связано с тем, что влияние скорости движения воды по отношению к повороту уменьшается.
Смотрел в разных книгах по местным сопротивлениям для поворота трубы и отводов. И приходил часто к расчетам, что один сильный резкий поворот равен коэффициенту единице. Резким поворотом считается, если радиус поворота по значению не превышает диаметр. Если радиус превышает диаметр в 2-3 раза, то значение коэффициента значительно уменьшается.
Подробней об этом в разделе: Местные гидравлические сопротивления
Возьмем ζ = 1.
Скорость 1,91 м/с
h=ζ•(V2)/2•9,81=(1•1,912)/( 2•9,81)=0,18 м.
Это значение умножаем на количество отводов и получаем 0,18•21=3,78 м.
Ответ: при скорости движения 1,91 м/с, получаем потерю напора 3,78 метров.
Давайте теперь решим целиком задачку с отводами.
При расходе 45 м3/час получили потерю напора по длине: 10,46 м. Смотри выше.
При этой скорости (2,29 м/с) находим сопротивление на поворотах:
h=ζ•(V2)/2•9,81=(1•2,292)/(2•9,81)=0,27 м. умножаем на 21 = 5,67 м.
Складываем потери напора: 10,46+5,67=16,13м.
Отмечаем на графике:

Решаем тоже самое только для расхода в 55 м3/ч
Q=55 м3/ч = 0,015 м3/сек.
V = (4•0,015)/(3,14•0,1•0,1)=1,91 м/с
Re=(V*D)/ν=(1,91 •0,1)/0,00000116=164655
λ=0,11( Δэ/D + 68/Re )0.25=0,11•( 0,0001/0,1 + 68/164655)0,25=0,0213
h=λ•(L•V2)/(D•2•g)= 0,0213•(376•1,91•1,91)/(0,1•2•9,81)=14,89 м.
h=ζ•(V2)/2•9,81=(1•1,912)/( 2•9,81)=0,18 м. умножаем на 21 = 3,78 м.
Складываем потери: 14,89+3,78=18,67 м
Рисуем на графике:

Ответ: Максимальный расход=52 м3/час. Без отводов Qmax=54 м3/час.
Чтобы в ручную не считать всю математику я приготовил специальную программу:
Скачать калькулятор расчетов гидравлического сопротивления.
Теперь я думаю вам понятно как происходит сопротивление движению потока. Если не понятно, то я готов услышать ваши коментарии по данной статье. Пишите коментарии.
В итоге, на размер диаметра влияют:
1. Сопротивление, создаваемое трубой с поворотами
2. Необходимый расход
3. Влияние насоса его расходно-напорной характеристикой
Если расход в конце трубы меньше, то необходимо: Либо увеличить диаметр, либо увеличить мощность насоса. Увеличивать мощность насоса не экономично.
Вычисляем диаметр трубы для отопления
Данная статья является частью системы: Конструктор водяного отопления
Все о дачном доме
Водоснабжение
Обучающий курс. Автоматическое водоснабжение своими руками. Для чайников.
Неисправности скважинной автоматической системы водоснабжения.
Водозаборные скважины
Ремонт скважины? Узнайте нужен ли он!
Где бурить скважину – снаружи или внутри?
В каких случаях очистка скважины не имеет смысла
Почему в скважинах застревают насосы и как это предотвратить
Прокладка трубопровода от скважины до дома
100% Защита насоса от сухого хода
Отопление
Обучающий курс. Водяной теплый пол своими руками. Для чайников.
Теплый водяной пол под ламинат
Обучающий Видеокурс: По ГИДРАВЛИЧЕСКИМ И ТЕПЛОВЫМ РАСЧЕТАМ
Водяное отопление
Виды отопления
Отопительные системы
Отопительное оборудование, отопительные батареи
Система теплых полов
Личная статья теплых полов
Принцип работы и схема работы теплого водяного пола
Проектирование и монтаж теплого пола
Водяной теплый пол своими руками
Основные материалы для теплого водяного пола
Технология монтажа водяного теплого пола
Система теплых полов
Шаг укладки и способы укладки теплого пола
Типы водных теплых полов
Все о теплоносителях
Антифриз или вода?
Виды теплоносителей (антифризов для отопления)
Антифриз для отопления
Как правильно разбавлять антифриз для системы отопления?
Обнаружение и последствия протечек теплоносителей
Как правильно выбрать отопительный котел
Тепловой насос
Особенности теплового насоса
Тепловой насос принцип работы
Запас мощности котла. Нужен ли он?
Про радиаторы отопления
Способы подключения радиаторов. Свойства и параметры.
Как рассчитать колличество секций радиатора?
Рассчет тепловой мощности и количество радиаторов
Виды радиаторов и их особенности
Автономное водоснабжение
Схема автономного водоснабжения
Устройство скважины Очистка скважины своими руками
Опыт сантехника
Подключение стиральной машины
Полезные материалы
Редуктор давления воды
Гидроаккумулятор. Принцип работы, назначение и настройка.
Автоматический клапан для выпуска воздуха
Балансировочный клапан
Перепускной клапан
Трехходовой клапан
Трехходовой клапан с сервоприводом ESBE
Терморегулятор на радиатор
Сервопривод коллекторный. Выбор и правила подключения.
Виды водяных фильтров. Как подобрать водяной фильтр для воды.
Обратный осмос
Фильтр грязевик
Обратный клапан
Предохранительный клапан
Смесительный узел. Принцип работы. Назначение и расчеты.
Расчет смесительного узла CombiMix
Гидрострелка. Принцип работы, назначение и расчеты.
Бойлер косвенного нагрева накопительный. Принцип работы.
Расчет пластинчатого теплообменника
Рекомендации по подбору ПТО при проектировании объектов теплоснабжения
О загрязнение теплообменников
Водонагреватель косвенного нагрева воды
Магнитный фильтр – защита от накипи
Инфракрасные обогреватели
Радиаторы. Свойства и виды отопительных приборов.
Виды труб и их свойства
Незаменимые инструменты сантехника
Интересные рассказы
Страшная сказка о черном монтажнике
Технологии очистки воды
Как выбрать фильтр для очистки воды
Поразмышляем о канализации
Очистные сооружения сельского дома
Советы сантехнику
Как оценить качество Вашей отопительной и водопроводной системы?
Профрекомендации
Как подобрать насос для скважины
Как правильно оборудовать скважину
Водопровод на огород
Как выбрать водонагреватель
Пример установки оборудования для скважины
Рекомендации по комплектации и монтажу погружных насосов
Какой тип гидроаккумулятора водоснабжения выбрать?
Круговорот воды в квартире
фановая труба
Удаление воздуха из системы отопления
Гидравлика и теплотехника
Введение
Что такое гидравлический расчет?
Невязка гидравлического расчета
Физические свойства жидкостей
Гидростатическое давление
Поговорим о сопротивлениях прохождении жидкости в трубах
Режимы движения жидкости (ламинарный и турбулентный)
Гидравлический расчет на потерю напора или как рассчитать потери давления в трубе
Местные гидравлические сопротивления
Профессиональный расчет диаметра трубы по формулам для водоснабжения
Как подобрать насос по техническим параметрам
Профессиональный расчет систем водяного отопления. Расчет теплопотерь водяного контура.
Гидравлические потери в гофрированной трубе
Теплотехника. Речь автора. Вступление
Процессы теплообмена
Тплопроводность материалов и потеря тепла через стену
Как мы теряем тепло обычным воздухом?
Законы теплового излучения. Лучистое тепло.
Законы теплового излучения. Страница 2.
Потеря тепла через окно
Факторы теплопотерь дома
Начни свое дело в сфере систем водоснабжения и отопления
Вопрос по расчету гидравлики
Конструктор водяного отопления
Диаметр трубопроводов, скорость течения и расход теплоносителя.
Вычисляем диаметр трубы для отопления
Расчет потерь тепла через радиатор
Мощность радиатора отопления
Расчет мощности радиаторов. Стандарты EN 442 и DIN 4704
Расчет теплопотерь через ограждающие конструкции
Найти теплопотери через чердак и узнать температуру на чердаке
Подбираем циркуляционный насос для отопления
Перенос тепловой энергии по трубам
Расчет гидравлического сопротивления в системе отопления
Распределение расхода и тепла по трубам. Абсолютные схемы.
Расчет сложной попутной системы отопления
Расчет отопления. Популярный миф
Расчет отопления одной ветки по длине и КМС
Расчет отопления. Подбор насоса и диаметров
Расчет отопления. Двухтрубная тупиковая
Расчет отопления. Однотрубная последовательная
Расчет отопления. Двухтрубная попутная
Расчет естественной циркуляции. Гравитационный напор
Расчет гидравлического удара
Сколько выделяется тепла трубами?
Собираем котельную от А до Я…
Система отопления расчет
Онлайн калькулятор Программа расчет Теплопотерь помещения
Гидравлический расчет трубопроводов
История и возможности программы – введение
Как в программе сделать расчет одной ветки
Расчет угла КМС отвода
Расчет КМС систем отопления и водоснабжения
Разветвление трубопровода – расчет
Как в программе рассчитать однотрубную систему отопления
Как в программе рассчитать двухтрубную систему отопления
Как в программе рассчитать расход радиатора в системе отопления
Перерасчет мощности радиаторов
Как в программе рассчитать двухтрубную попутную систему отопления. Петля Тихельмана
Расчет гидравлического разделителя (гидрострелка) в программе
Расчет комбинированной цепи систем отопления и водоснабжения
Расчет теплопотерь через ограждающие конструкции
Гидравлические потери в гофрированной трубе
Гидравлический расчет в трехмерном пространстве
Интерфейс и управление в программе
Три закона/фактора по подбору диаметров и насосов
Расчет водоснабжения с самовсасывающим насосом
Расчет диаметров от центрального водоснабжения
Расчет водоснабжения частного дома
Расчет гидрострелки и коллектора
Расчет Гидрострелки со множеством соединений
Расчет двух котлов в системе отопления
Расчет однотрубной системы отопления
Расчет двухтрубной системы отопления
Расчет петли Тихельмана
Расчет двухтрубной лучевой разводки
Расчет двухтрубной вертикальной системы отопления
Расчет однотрубной вертикальной системы отопления
Расчет теплого водяного пола и смесительных узлов
Рециркуляция горячего водоснабжения
Балансировочная настройка радиаторов
Расчет отопления с естественной циркуляцией
Лучевая разводка системы отопления
Петля Тихельмана – двухтрубная попутная
Гидравлический расчет двух котлов с гидрострелкой
Система отопления (не Стандарт) – Другая схема обвязки
Гидравлический расчет многопатрубковых гидрострелок
Радиаторная смешенная система отопления – попутная с тупиков
Терморегуляция систем отопления
Разветвление трубопровода – расчет
Гидравлический расчет по разветвлению трубопровода
Расчет насоса для водоснабжения
Расчет контуров теплого водяного пола
Гидравлический расчет отопления. Однотрубная система
Гидравлический расчет отопления. Двухтрубная тупиковая
Бюджетный вариант однотрубной системы отопления частного дома
Расчет дроссельной шайбы
Что такое КМС?
Расчет гравитационной системы отопления
Конструктор технических проблем
Удлинение трубы
Требования СНиП ГОСТы
Требования к котельному помещению
Вопрос слесарю-сантехнику
Полезные ссылки сантехнику
—
Сантехник – ОТВЕЧАЕТ!!!
Жилищно коммунальные проблемы
Монтажные работы: Проекты, схемы, чертежи, фото, описание.
Если надоело читать, можно посмотреть полезный видео сборник по системам водоснабжения и отопления