Как найти скорость при равноускоренном движении формула - Сайт, где вы сможете решить свои вопросы

Равноускоренное движение в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного падения

Равноуско́ренное движе́ние — движение тела, при котором его ускорение постоянно по модулю и направлению^[1].

Скорость при этом определяется формулой

${displaystyle {vec {v}}(t)={vec {v}}_{0}+{vec {a}}t}$

где ${displaystyle {vec {v}}_{0}}$ — начальная скорость тела, — время. Траектория имеет вид участка параболы или прямой.

Примером такого движения является полёт камня, брошенного под углом alpha к горизонту в однородном поле силы тяжести: камень летит с постоянным ускорением , направленным вертикально вниз.

Частным случаем равноускоренного движения является равнозамедленное, когда векторы vec{v} и противонаправлены, а модуль скорости равномерно уменьшается со временем (в примере с камнем реализуется для ${displaystyle alpha =90^{0}}$ при подъёме).

Характер равноускоренного движения[править | править код]

Равноускоренное движение происходит в плоскости, содержащей векторы ускорения и начальной скорости ${displaystyle {vec {v}}_{0}}$ . С учётом того, что (здесь — радиус-вектор), траектория описывается выражением

${displaystyle {vec {r}}(t)={vec {r}}_{0}+{vec {v}}_{0}t+{frac {{vec {a}}t^{2}}{2}}}$

На заданном интервале времени она представляет собой участок параболы, который при параллельности (то есть со или противо- направленности) векторов и ${displaystyle {vec {v}}_{0}}$ превращается в отрезок прямой.

Для каждой из координат, скажем , могут быть записаны аналогичные по структуре выражения:

${displaystyle y(t)=y_{0}+v_{0y}t+{frac {a_{y}t^{2}}{2}}}$

где ${displaystyle a_{y}}$ — составляющая ускорения вдоль оси , а ${displaystyle {vec {r}}_{0}=x_{0}{vec {i}}+y_{0}{vec {j}}+z_{0}{vec {k}}}$ — радиус-вектор материальной точки в момент ( vec{i} , vec{j} , vec{k} — орты).

В примере с камнем ${displaystyle x_{0}=y_{0}=z_{0}=0}$ , компоненты ускорения ${displaystyle a_{x}=a_{z}=0}$ , ${displaystyle a_{y}=-g}$ , начальной скорости ${displaystyle v_{x0}=v_{0}cos alpha }$ , ${displaystyle v_{y0}=v_{0}sin alpha }$ , ${displaystyle v_{z0}=0}$ , при этом ${displaystyle x(t)=v_{0x}t}$ , а значит, ${displaystyle y=operatorname {tg} alpha cdot x-g/2v_{0}^{2}cos ^{2}alpha cdot x^{2}}$ .

Перемещение и скорость[править | править код]

В случае равноускоренного движения любая из компонент скорости, например ${displaystyle v_{x}}$ , зависит от времени линейно:

${displaystyle v_{x}=v_{0x}+a_{x}t}$

При этом имеет место следующая связь между перемещением ( ${displaystyle Delta x=x-x_{0}}$ ) вдоль координаты и скоростью вдоль той же координаты:

$Delta x={frac {v_{x}^{2}-v_{{0x}}^{2}}{2a_{x}}}$

Отсюда можно получить выражение для -составляющей конечной скорости тела при известных -составляющих начальной скорости и ускорения:

$v_{x}=pm {sqrt {v_{{0x}}^{2}+2a_{x}Delta x}}$

Если ${displaystyle a_{x}=0}$ , то ${displaystyle v_{x}=v_{ox}}$ , а ${displaystyle Delta x=v_{0x}t}$ .

Выражения для смещений Delta y , Delta z и компонент скорости вдоль координат и принимают точно такой же вид, как для Delta x и $v_{x}$ , но символ всюду заменяется на или .

Суммарно, по теореме Пифагора, перемещение составит

${displaystyle |Delta {vec {r}}|={sqrt {(Delta x)^{2}+(Delta y)^{2}+(Delta z)^{2}}}}$

а модуль конечной скорости находится как

$|{vec v}|={sqrt {v_{{x}}^{2}+v_{{y}}^{2}+v_{{z}}^{2}}}$

Равноускоренное движение не может происходить неограниченно долго: это означало бы, что, начиная с какого-то момента времени , модуль скорости тела превысит величину скорости света в вакууме , что исключается теорией относительности.

Условие осуществления[править | править код]

Равноускоренное движение реализуется при действии на тело (материальную точку) постоянной силы vec{F} , обычно в однородном гравитационном или электростатическом поле, если величина скорости тела значительно меньше, чем скорость света . Тогда, по второму закону Ньютона, ускорение составит

${vec {a}}={frac {{vec {F}}}{m}},$

где через обозначена масса тела. В примере с камнем роль vec{F} играет сила тяжести.

Если же скорость тела сопоставима со скоростью света, то закон Ньютона в выписанном виде неприменим. При этом, в случае действия постоянной силы, происходит так называемое релятивистски равноускоренное движение, при котором постоянно только собственное ускорение, а ускорение в фиксированной ИСО приближается к нулю со временем по мере приближения величины скорости к её пределу .

Теорема о кинетической энергии точки[править | править код]

Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:

$ma_{x}Delta x={frac {mv_{x}^{2}}{2}}-{frac {mv_{{0x}}^{2}}{2}}$

Записав аналогичные соотношения для координат и и просуммировав все три равенства, получим соотношение:

${displaystyle {vec {F}}cdot Delta {vec {r}}={frac {mv^{2}}{2}}-{frac {mv_{0}^{2}}{2}}}$

Слева стоит работа постоянной равнодействующей силы vec F , а справа — разность кинетических энергий в конечный и начальный моменты движения. Полученная формула представляет собой математическое выражение теоремы о кинетической энергии точки для случая равноускоренного движения^[2].

Равнопеременное движение[править | править код]

Равнопеременным называется движение, при котором тангенциальная (параллельная скорости) составляющая ускорения постоянна^[3]. Такое движение не является равноускоренным, кроме ситуации, когда оно происходит по прямой, но в математическом плане может быть рассмотрено аналогично.

В этом случае вводится обобщённая координата , часто называемая путём, соответствущая длине пройденной траектории (длине дуги кривой). Таким образом, формула приобретает вид:

$Delta S={frac {v^{2}-v_{{0}}^{2}}{2a_{tau }}}$

где $a_{tau }$ — тангенциальное ускорение, «отвечающее» за изменение модуля скорости тела. Для скорости получаем:

$v=pm {sqrt {v_{{0}}^{2}+2a_{tau }Delta S}}$

При ${displaystyle a_{tau }=0}$ имеем движение с постоянной по модулю скоростью.

Иногда прилагательное равнопеременное заменяют на криволинейное равноускоренное, что вносит путаницу, так как, скажем, равноускоренное движение камня по кривой (параболе) в поле тяжести не равнопеременное.

См. также[править | править код]

Релятивистски равноускоренное движение

Примечания[править | править код]

↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 37. — 560 с. — ISBN 5-9221-0225-7.
↑ Тарг С. М. Краткий курс теоретической механики. — 11-е изд. — М.: «Высшая школа», 1995. — С. 214. — 416 с. — ISBN 5-06-003117-9.
↑ См. Физический энциклопедический словарь — М.: Советская энциклопедия, под. ред. А. М. Прохорова (1983), статья «Равнопеременное движение», стр. 602.

Источник

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.

Примеры равноускоренного движения:

разгон самолета перед взлетом;
падающая с крыши сосулька;
торможение лыжника на горном склоне;
разгоняющийся на склоне сноубордист;
свободное падение в результате прыжка с парашютом;
камень брошенный под углом к горизонту;

Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

V_к=V_н+at

где: V_к — конечная скорость тела,
V_н — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.

Формула для ускорения при равноускоренном движении:

a=(V_к-V_н)/t

Во время движения тела ускорение остается постоянным.

Задача 1

Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.

Формула расстояния при равноускоренном движении

Если известны время, скорость начальная и скорость конечная

S = t*(V_н+ V_к)/2

Если известны время, скорость начальная и ускорение

S = V_нt + at²/2 **= t*(V_н + at/2)**

где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

2аS = V_к²−V_н²

где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.

Задача 2

Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.

Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.

Равноускоренное движение: графически

График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.

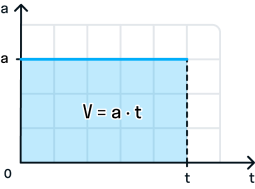
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.

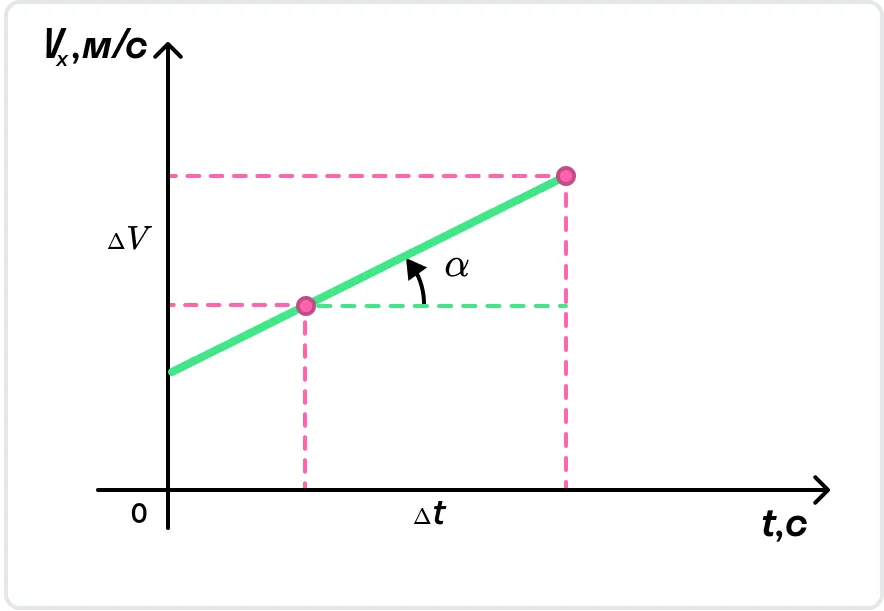
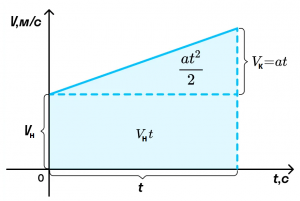
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V_нt и треугольника at²/2. Получим: S = V_нt + at²/2.

Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.

Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = V_к²−V_н²
Получим: а = (V_к²−V_н² )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = V_нt + at²/2.
Получаем: x(t) = 3t + 1,5t²
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*2² =6+6=12 м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.

Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:

Конвертер единиц измерения расстояния (длины)
Конвертер единиц измерения скорости
Конвертер единиц измерения времени

Источник

Равноускоренное движение.

Зависимость скорости от времени.
Закон движения.
Прямолинейное равноускоренное движение.
Свободное падение.
Горизонтальный бросок.
Бросок под углом к горизонту.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.

Равноускоренное движение – это движение с постоянным вектором ускорения vec a . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.

к оглавлению ▴

Зависимость скорости от времени.

При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.

Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:

$frac{displaystyle dvec{v}}{displaystyle dt}=vec{a}$ . (1)

В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор vec a ? Разумеется, функцию vec a t . Но не только: к ней можно добавить ещё произвольный постоянный вектор vec c (ведь производная постоянного вектора равна нулю). Таким образом,

. (2)

Каков смысл константы vec c ? В начальный момент времени t=0 скорость равна своему начальному значению: $vec v=vec v_{0}$ . Поэтому, полагая t=0 в формуле (2), получим:

$vec v_{0}=vec c$ .

Итак, константа vec c – это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:

$vec v=vec v_{0}+vec {a}t$ . (3)

В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:

$v_{displaystyle x}=v{displaystyle 0x}+a_{displaystyle x}t$ , (4)

$v_{displaystyle y}=v{displaystyle 0y}+a_{displaystyle y}t$ . (5)

Формула для третьей компоненты скорости, $v_{displaystyle z}$ если она необходима, выглядит аналогично.)

к оглавлению ▴

Закон движения.

Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:

$frac{displaystyle dvec{r}}{displaystyle dt}=vec{v}$

Подставляем сюда выражение для скорости, даваемое формулой (3):

$frac{displaystyle dvec{r}}{displaystyle dt}=vec v_{0}+vec {a}t$ (6)

Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить $vec v_{0}$ , надо продифференцировать функцию $vec v_{0}t$ . Чтобы получить , нужно продифференцировать $vec {a} t^{2} /2$ . Не забудем добавить и произвольную константу vec c :

$vec r=vec c+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

Ясно, что vec c – это начальное значение $vec r_{0}$ радиус-вектора vec r в момент времени t=0 . В результате получаем искомый закон равноускоренного движения:

$vec r=vec r_{0}+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ . (7)

Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ . (8)

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ . (9)

$z=z_{0}+ v_{displaystyle 0z} t+frac{displaystyle a_{displaystyle z} t^{2}}{displaystyle 2}$ . (10)

Формулы (8) – (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.

Снова вернёмся к закону движения (7). Заметим, что $vec r - vec r_{0}=vec s$ – перемещение тела. Тогда
получаем зависимость перемещения от времени:

$vec s= vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

к оглавлению ▴

Прямолинейное равноускоренное движение.

Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:

$v_{displaystyle x}=v_{displaystyle 0x}+a_{displaystyle x}t$ ,

$x=x_{0}+ v_{0 displaystyle x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$s_{x}= v_{0x} t+frac{displaystyle a_{x} t^{2}}{displaystyle 2}$ ,

где $s_{x}= x-x_{0}$ – проекция перемещения на ось .

Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:

$t=frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}$

и подставим в формулу для перемещения:

$s_{x}= v_{0x} frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}+frac{displaystyle a_{x}}{2} (frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}})^{2}$ .

После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:

$s_{x}=frac{displaystyle v_{displaystyle x}^{displaystyle 2}-displaystyle v_{displaystyle 0x}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}$ .

Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.

к оглавлению ▴

Свободное падение.

Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.

Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения vec g , направленным вертикально вниз. Почти во всех задачах при расчётах полагают g=10 м/с $^{2}$ .

Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.

Задача. Найти скорость приземления дождевой капли, если высота тучи h=2 км.

Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой

$s_{y}=frac{displaystyle v_{displaystyle y}^{displaystyle 2}-displaystyle v_{displaystyle 0y}^{displaystyle 2}}{displaystyle 2a_{displaystyle y}}$ .

Имеем: $s_{y}=h, v_{y}=v$ – искомая скорость приземления, $v_{0y}=0, a_{y}=g$ . Получаем: $h^{2}=frac{v^{2}}{2g}$ , откуда . Вычисляем: м/с. Это 720 км/ч, порядка скорости пули.

На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!

Задача. Тело брошено вертикально вверх со скоростью $v_{0}=30$ м/с. Найти его скорость через t=5 c.

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$v_{displaystyle y}=v_{displaystyle 0y}+a_{displaystyle y}t$ .

Здесь $v_{displaystyle 0y}=v_{0}, a_{y}=-g$ , так что $v_{displaystyle y}=v_{displaystyle 0}-gt$ . Вычисляем: $v_{displaystyle y}=30-10 cdot 5=-20$ м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.

Задача. С балкона, находящегося на высоте h=15 м, бросили вертикально вверх камень со скоростью $v_{0}=10$ м/с. Через какое время камень упадёт на землю?

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

Имеем: $y=0, y_{0} = h, v_{0y}=v_{0}, a_{y}=-g,$ так что $0=h+v_{0}t-frac{displaystyle g t^{2}}{displaystyle 2}=15+10t-5t^{2}$ , или $t^{2}-2t-3=0$ . Решая квадратное уравнение, получим t=3 c.

к оглавлению ▴

Горизонтальный бросок.

Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.

Предположим, что тело брошено горизонтально со скоростью $v_{0}$ с высоты . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.

Выберем систему координат OXY так, как показано на рис. 1.

Рис. 1. Горизонтальный бросок

Используем формулы:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$

В нашем случае $x_{0} = 0, v_{0x}=v_{0}, a_{x}=0, y_{0} = h, v_{0y}=0, a_{y}=-g$ . Получаем:

$x=v_{0}t, y=h-frac{displaystyle g t^{2}}{displaystyle 2}$ . (11)

Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:

$y(T)=0Rightarrow h-frac{displaystyle gT^{displaystyle 2}}{displaystyle 2}=0Rightarrow T=sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Дальность полёта – это значение координаты в момент времени :

$L=x(T)=v_{0}T=v_{0} sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:

$t=frac{displaystyle x}{displaystyle v_{displaystyle 0}}Rightarrow y=h-frac{displaystyle g}{displaystyle 2}(frac{displaystyle x}{displaystyle v_{displaystyle 0}})^{displaystyle 2}=displaystyle h-frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{displaystyle 0}}$ .

Получили зависимость от , которая является уравнением параболы. Следовательно, тело летит по параболе.

к оглавлению ▴

Бросок под углом к горизонту.

Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.

Предположим, что тело брошено с поверхности Земли со скоростью $v_{0}$ , направленной под углом alpha к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.

Выберем систему координат OXY так, как показано на рис. 2.

Рис. 2. Бросок под углом к горизонту

Начинаем с уравнений:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

В нашем случае $x_{0} =y_{0}=0, v_{0x}=v_{0}cos alpha, v_{0y}=v_{0}sin alpha , a_{x}=0, a_{y}=-g$ . Получаем:

$x=(v_{0}cos alpha )t, y=(v_{0}sin alpha)t- frac{displaystyle g t^{2}}{displaystyle 2}$ .

Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:

$T=frac{displaystyle 2v_{displaystyle 0}sinalpha }{displaystyle g}$ ,

$L=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin2alpha }{displaystyle g}$ ,

$y=x tgalpha -frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{0}cos^{displaystyle 2}alpha }$ .

(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:

$H=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin^{2} alpha }{displaystyle 2g}$ .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Равноускоренное движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Скорость при равноускоренном движении

4.2

Средняя оценка: 4.2

Всего получено оценок: 180.

4.2

Средняя оценка: 4.2

Всего получено оценок: 180.

Одним из частых видов движений, происходящих в Природе, является равноускоренное движение. Рассмотрим особенности определения скорости при равноускоренном движении.

Равноускоренное движение

Равноускоренное движение – это движение с постоянным ускорением. Напомним, что ускорение – это отношение изменения скорости за некоторый промежуток времени к величине этого промежутка:

$$overrightarrow a = {overrightarrow v- overrightarrow v_0 over t}$$

Если ускорение за любой промежуток времени одинаково, то такое движение называется равноускоренным. В обычной жизни движение с увеличивающейся скоростью называется движением с ускорением, а с уменьшающейся скоростью – движением с замедлением. Однако, в механике оба этих движения (при условии, что ускорение остается постоянным) называются равноускоренным.

Рис. 1. Примеры равноускоренного движения

Мгновенная скорость при равноускоренном движении

Мгновенную скорость при равноускоренном движении можно найти из формулы ускорения, перенеся все известные величины в правую часть:

$$overrightarrow v = overrightarrow v_0 + overrightarrow a t$$

Это основная формула скорости при равноускоренном движении.

В случае прямолинейного движения все векторы направлены вдоль одной прямой, модули проекций равны модулям векторов. В случае движения на плоскости – необходимо рассматривать проекции на каждую ось.

График скорости при равноускоренном движении

Из приведенной формулы скорости можно сделать важные выводы относительно ее графика.

График скорости представляет собой прямую. Значение скорости монотонно возрастает или убывает.
График скорости восходящий для положительного ускорения и нисходящий для отрицательного.
Если тело двигалось с начальной скоростью $v_0$, то график скорости пересекает ось ординат в точке с координатой $v_0$. Если начальная скорость тела равна нулю, график скорости пересечет начало координат.

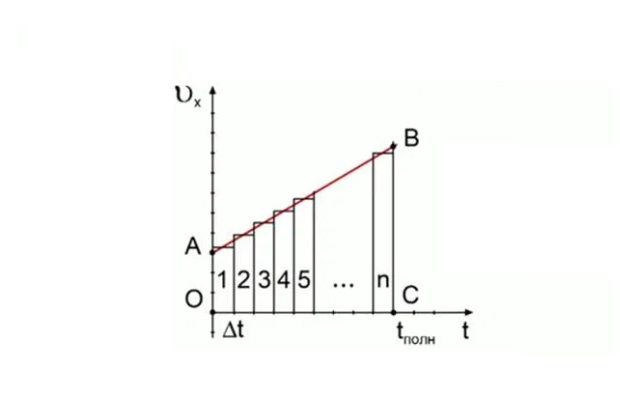
Рис. 2. Пример графика скорости равноускоренного движения

Еще одно важное заключение можно сделать, если учесть, что площадь фигуры, ограниченной графиком скорости и осью абсцисс, равна пройденному пути. Эта фигура в общем случае представляет собой трапецию, где высота – это значение времени, а основания – это значения скорости, линейно зависящие от времени. При перемножении этих величин мы получим значение, зависящее от квадрата времени. То есть, пройденный путь при равноускоренном движении пропорционален квадрату времени.

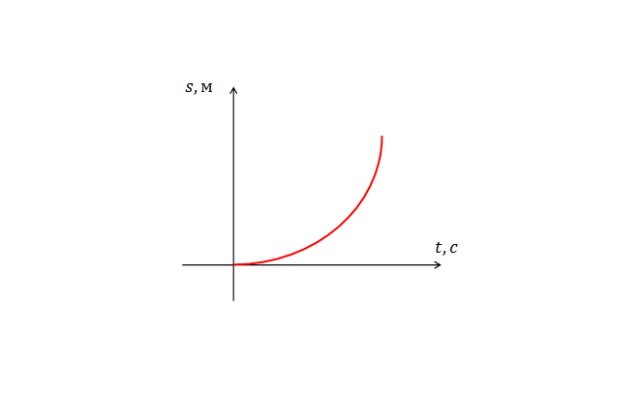
Рис. 3. Пример графика пути при равноускоренном движении

Наиболее частым равноускоренным движением, которое встречается в Природе, является свободное падение тел в первые секунды полета, когда сопротивление воздуха пренебрежительно мало.

Что мы узнали?

При равноускоренном движении скорость монотонно возрастает или убывает со временем. График скорости равноускоренного движения представляет собой прямую, восходящую, если проекция ускорения положительна, или нисходящую, если проекция ускорения отрицательна.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.2

Средняя оценка: 4.2

Всего получено оценок: 180.

А какая ваша оценка?

Источник

Характер равноускоренного движения[править | править код]

Перемещение и скорость[править | править код]

Условие осуществления[править | править код]

Теорема о кинетической энергии точки[править | править код]

Равнопеременное движение[править | править код]

См. также[править | править код]

Примечания[править | править код]

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

Vк=Vн+at

Формула для ускорения при равноускоренном движении:

a=(Vк-Vн)/t

Задача 1

Формула расстояния при равноускоренном движении

S = t*(Vн+ Vк)/2

S = Vнt + at2/2 = t*(Vн + at/2)

2аS = Vк2−Vн2

Задача 2

Перемещение при равноускоренном движении

Равноускоренное движение: графически

Задача 3

Равноускоренное движение.

Зависимость скорости от времени.

Закон движения.

Прямолинейное равноускоренное движение.

Свободное падение.

Горизонтальный бросок.

Бросок под углом к горизонту.

Скорость при равноускоренном движении

Равноускоренное движение

Мгновенная скорость при равноускоренном движении

График скорости при равноускоренном движении

Что мы узнали?

Тест по теме

Оценка доклада

Вам также может понравиться

Как найти дискриминант куба

Как составить интересный доклад

Сливки свернулись при тушении как исправить

Добавить комментарий Отменить ответ

V_к=V_н+at

a=(V_к-V_н)/t

S = t*(V_н+ V_к)/2

S = V_нt + at²/2 **= t*(V_н + at/2)**

2аS = V_к²−V_н²