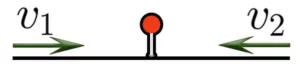
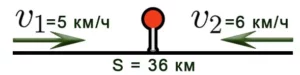
Для решения задач на движение стоит прояснить объекты сближаются или удаляются, ответ зависит от вида движения. Когда объекты двигаются навстречу друг другу из разных пунтков, то они сближаются:
(v_1+v_2=20+30=50) км/час скорость сближения
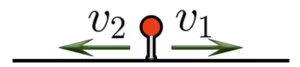
Когда объекты двигаются в противоположных направлениях из одного пункта, то они удаляются:
(v_1+v_2=20+30=50) км/час скорость удаления
Когда объекты двигаются в одном направление одновременно:
- Если они выезжают одновременно, то два объекта удаляются друг от друга, так как скорость у них разная, для того чтобы найти скорость их удаления надо из большей скорости вычесть меньшую.
(v_y=v_2-v_1)
- Если они выезжают с интервалом, то два объекта могут удаляться или сближаться в зависимости от их скоростей:
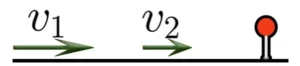
1) если скорость объекта, который впереди больше, то они удаляются. (v_2>v_1)
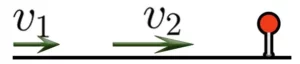
2) если скорость объекта, который впереди меньше, то они сближаются . (v_1>v_2)
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
В 4 классе дети начинают решать задачи на скорость сближения и скорость удаления. Ребята начинают путаться. Часто они не могут определить вид задачи или просто не знают формулы. Однако понять эту тему легко. В этой статье Я расскажу, как учу своих учеников не путаться в задачах данного вида.
Ситуация 1
Представь, что вы с мамой вышли из дома и пошли в разные стороны. Вы будете приближаться друг к другу или удаляться друг от друга? Удаляться. Расстояние между вами будет увеличиваться или уменьшаться? Увеличиваться. Для того, чтобы найти скорость удаления в данной ситуации, нужно две скорости сложить.
Задача
Из города одновременно в разных направлениях выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 + 70 = 160 (км/ч) – скорость удаления.
2) 160 × 4 = 640 (км)
Ответ: 640 км будет расстояние между автомобилями через 4 часа.
Ситуация 2
Представь, что вы с мамой идете навстречу друг другу.
В каждой из обсуждаемых ситуаций я задаю одни и те же вопросы, как в первой ситуации. Поэтому дальше я буду писать только результат наших рассуждений.
Когда мы идем навстречу друг другу, мы приближаемся друг к другу. Поэтому ищем скорость сближения. Расстояние между нами будет становиться меньше. Для того, чтобы найти скорость сближения в данной ситуации, нужно скорости сложить.
Задача
Расстояние между двумя городами 640 км. Из каждой из них одновременно навстречу друг другу выехали два автомобиля. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Через сколько часов автомобили встретятся?
1) 90 + 70 = 160 (км/ч) – скорость сближения
2) 640 : 160 = 4 (ч)
Ответ: автомобили встретятся через 4 часа.
Ситуация 3
Представь, что ты идешь по улице и видишь, что впереди идет мама. Ты решаешь ее догнать. Твоя скорость больше, чем скорость мамы. Ты догонишь маму? Да. Вы будете приближаться к друг другу или удаляться?Расстояние между вами будет увеличиваться или уменьшаться? Уменьшаться. (приближаться, т. к. ребенок сокращает расстояние). В этой ситуации мы находим скорость сближения.
Задача
Из города в посёлок выехали два автомобиля. Скорость первого автомобиля 70 км/ч, скорость второго автомобиля 90 км/ч. Через сколько часов второй автомобиль догонит первый, если расстояние между ними равно 120 км?
1) 90 – 70 = 20 (км/ч) – скорость сближения
2) 120 : 20 = 6 ( ч)
Ответ: второй автомобиль догонит первый через 6 часов.
Ситуация 4
Представь ту же ситуацию, но теперь скорость больше у мамы. Ты догонишь маму? Нет. Почему? Она будет постоянно удаляться. Находим скорость удаления. Для этого из большей скорости вычитаем меньшую.
Задача
Одновременно из города выехали два автомобиля и поехали в одном направлении. Скорость первого автомобиля 90 км/ч, скорость второго автомобиля 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
1) 90 – 70 = 20 (км/ч) – скорость удаления
2) 20 × 4 = 80 (км)
Ответ: 80 км будет расстояние между автомобилями через 4 часа.
Делитесь своим мнением в комментариях, подписывайтесь на мой канал
Если они движутся в одном направлении, объекты могут находиться как близко, так и далеко друг от друга. В этом случае они как бы «конкурируют» за общую дистанцию и «действуют друг против друга». Поэтому их общая скорость равна их разности скоростей.
Решение задач на движение. Формулы, схемы, встречное движение
Очень легко рисовать диаграммы для задач на движение. Они помогают визуализировать проблему и найти правильное решение. В сложных случаях или если ученик не может найти решение, рекомендуется дополнить диаграмму таблицей, в которой параметры скорости, времени и расстояния указаны в заголовке. Подробнее об этом ниже.
- Простые задачи на движение
- Решение
- Обратные задачи на движение
- Как найти скорость, если известно время и расстояние
- Как найти время, когда известны скорость и расстояние
- Схемы задач на встречное движение
- Решение
- Задачи на движение в одном направлении
- Шпаргалка по решению задач на скорость, время и расстояние
Простые задачи на движение
Простые задачи о путешественниках, лыжниках, мотоциклистах и других движущихся объектах (есть даже задачи о черепахах) решаются уже в первых классах. На этих примерах легко понять, как составлять диаграммы.
Задача 1. Он прибыл в пункт B через 3 часа. Он дошел до точки А. Он шел со скоростью 5 км/ч. Каково расстояние между этими двумя точками?
Постройте диаграмму для решения задачи: Прямая линия, соединяющая точки A и B, является общим расстоянием. Стрелка показывает направление движения путешественника. Над стрелкой укажите скорость, если она известна. Поместите время или расстояние ниже (или выше) сегмента:
Если вы не смогли решить задачу с помощью диаграммы, я предлагаю вам воспользоваться таблицей:
| Скорость | Время | Расстояние |
| 5 км/ч | 3 ч | ? км |
Чтобы решить задачу с помощью таблицы, запомните правила:
- Чтобы найти расстояние, нужно скорость умножить на время: S = V x t
- Чтобы найти скорость, нужно расстояние разделить на время, (это производное из первой формулы: V = S : t )
- чтобы найти время, необходимо расстояние разделить на скорость. (также просто вывести из первой формулы: t = S : t
Решение
5 x 3 = 15 км — расстояние между пунктами A и B.
Обратные задачи на движение
Как найти скорость, если известно время и расстояние
Чтобы не запутаться в различных условиях задачи, составьте задачу в обратном порядке по сравнению с первым примером:
Задача 2: Расстояние между пунктами A и B равно 15 км. Путешественник преодолел это расстояние за 3 часа. С какой скоростью ехал путешественник?
| Скорость | Время | Расстояние |
| ? км/ч | 3 ч | 15 км |
Как найти время, когда известны скорость и расстояние
Задача 3 Расстояние между двумя точками равно 15 км. Пешеход двигался со скоростью 5 км/ч. Сколько времени потребуется пешеходу, чтобы пройти все расстояние?
| Скорость | Время | Расстояние |
| 5 км/ч | ? ч | 15 км |
Решение простых задач на движение: скорость, время и расстояние
В простых задачах на движение обычно имеется движущийся объект, для которого необходимо определить неизвестную величину: Скорость, время или расстояние. В этом случае формула применяется в своем первоначальном виде:
Задача 1. Автомобиль двигался со скоростью 85 км/ч в течение 2 часов. Первое задание дается в первой форме. Определите расстояние. Решение: Вычислите расстояние по формуле: S=V × t= 2 ч * 85 км/ч = 170 км.
Задача 2: Велосипедист проехал 60 км за 5 часов. Определите скорость. Решение: Рассчитайте скорость велосипедиста по следующей формуле: V = S:t = 60 км : 5 ч = 12 км/ч.
Задача 3: Мотоциклист проехал 30 км со скоростью 15 км/ч. Он проехал 30 км со скоростью 15 км/ч. Он проехал 30 км со скоростью 15 км/ч. Он проехал 30 км со скоростью 15 км/ч. Он проехал 30 км со скоростью 15 км/ч. Он ехал со скоростью 15 км/ч. Сколько времени ему понадобилось, чтобы преодолеть это расстояние? Решение: Рассчитайте время в пути мотоциклиста
Когда они движутся в противоположных направлениях, скорости объектов направлены в разные стороны. Объекты удаляются друг от друга со скоростью разделения. Скорость разделения определяется по следующей формуле:
При решении таких задач лучше всего нарисовать схему движения, чтобы облегчить решение.
Решение задач на движение в разных направлениях: сближение (встречное движение) и удаление (противоположное движение)
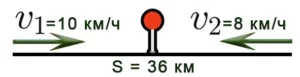
Задача 5: Два велосипедиста отправились в путь одновременно, чтобы встретиться в двух пунктах, расстояние между которыми 36 км. Скорость первого велосипедиста составляет 10 км/ч, а скорость второго велосипедиста — 8 км/ч. Через сколько часов они встретятся? Решение: 1) Определите скорость приближения: V = 10+8 = 18 км/ч. 2) Определите время: t = S:V = 36 : 18 = 2 ч.
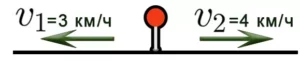
Задача 6: Два пешехода одновременно выходят из одного и того же места в противоположных направлениях. Скорость первого пешехода — 3 км/ч, второго — 4 км/ч. Каким будет расстояние между ними через 30 минут? Решение. 3) Найдите расстояние: S=V × t = 7 × 0,5 = 3,5 км.
Задача 7. Два автобуса одновременно выехали из двух пунктов, расстояние между которыми 300 км, на встречу. Они встретились через 2 часа. Найдите скорость второго автобуса, если первый автобус движется со скоростью 70 км/ч. Решение. 1) Мы знаем расстояние и скорость, поэтому найдите скорость по формуле. Это скорость конвергенции. 2) Определим скорость второго автобуса: 150-70 = 80 км/ч.
Когда два объекта движутся в одном направлении и один объект «догоняет» другой, расстояние между ними уменьшается. Скорость сближения в таком движении определяется по формуле:
Когда два объекта движутся в одном направлении и один объект «отстает» от второго, расстояние между ними увеличивается. Скорость отделения в этом типе движения определяется по следующей формуле: Если объект движется в стоячей воде, расстояние между объектами увеличивается:
Если объект движется в стоячей воде (озере), его скорость называется скоростью самого объекта. То есть скорость объекта равна собственной скорости объекта.
Решение задач на движение в одном направлении: сближение и удаление
Обратите внимание, что плот — это тело, скорость которого равна нулю (V=0). Таким образом, плот может плыть только по течению и со скоростью течения.
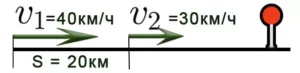
Проблема 8. Расстояние между двумя автомобилями, движущимися в одном направлении, составляет 20 км. Первый автомобиль движется со скоростью 40 км/ч, второй автомобиль движется со скоростью 30 км/ч. Через сколько часов первый автомобиль доедет до второго автомобиля? Решение. 1) Найдите скорость сближения машин.
2) Найдите время для расстояния (20 км) и скорости приближения (10 км/ч): 20:10=2 часа.
Задание 9. автомобиль
Как найти скорость сближения и скорость удаления? Ответ зависит от вида движения.
I. При движении навстречу друг другу объекты сближаются:
Чтобы найти скорость сближения, надо сложить скорости объектов:
II. При движении в противоположных направлениях объекты удаляются:
Чтобы найти скорость удаления, надо сложить скорости объектов:
III. При движении в одном направлении объекты могут как сближаться, так и удаляться.
Если объекты вышли одновременно из одного пункта с разными скоростями, то они удаляются.
Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Если объекты выходят одновременно из разных пунктов и движутся в одном направлении, то это — движение вдогонку.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются.
Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются:
Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Если из одного пункта в одном направлении выходит сначала один объект, а спустя некоторое время вслед за ним — другой, то рассуждаем аналогично: если скорость идущего впереди больше, то объекты удаляются, если скорость идущего впереди меньше — сближаются.
Обратите внимание:
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.

где:
- Скорость (V) — расстояние, пройденное за единицу времени.
- Время (t) — время в пути.
- Расстояние (S) — пройденный путь, или расстояние.
Зная эту формулу (для расстояния), вы можете легко вывести из неё формулу для скорости, или времени.
Если вы запомните эту формулу, то сможете решить любую задачу на движение, так как все задачи на движение по прямой — это применение данной формулы к одному или нескольким взаимосвязанным объектам.
Рассмотрим, как решать разные задачи на движение в зависимости от условий и уровня сложности.
Все задачи на движение делятся на следующие типы:
- простые задачи на скорость, время и расстояние;
- задачи на движение в разных направлениях: сближение и удаление;
- задачи на движение в одном направлении: сближение и удаление;
- решение задач на движение по реке.
Решение простых задач на движение: скорость, время и расстояние
В простых задачах на движение, как правило, есть один движущийся объект, для которого нужно найти неизвестную величину: скорость, время или расстояние. В данном случае применяется формула в ее первоначальном виде:
Задача 1. Автомобиль ехал 2ч со скоростью 85 км/ч. Определите расстояние.
Решение: Вычислим путь по формуле: S=V × t= 2 ч * 85 км/ч = 170 км.
Задача 2. Велосипедист проехал 60 км за 5ч. Определите скорость.
Решение: Вычислим скорость велосипедиста по формуле: V = S:t = 60 км : 5 ч = 12 км/ч.
Задача 3. Мотоциклист проехал 30 км со скоростью 15км/ч. Сколько времени он затратил на этот путь?
Решение: Вычислим время движения мотоциклиста по формуле: t = S:V = 30 км : 15 км/ч = 2 ч.
В таких задачах нужно также следить, чтобы были одинаковыми единицы измерения. Например, если расстояние измеряется в километрах, а время — в часах, то скорость буде измеряться в км/час. Но если единицы измерения скорости — метр/час, а время дано в минутах, то в этом случае скорость и время нужно привести к одинаковым единица измерения, иначе ответ будет неверным.
Задача 4. Мотоциклист ехал 30 минут со скоростью 60 км/ч. Какое расстояние он проехал?
Решение: для того, чтобы вычислить расстояние, нужно время и скорость привести к одинаковым единицам измерения. При этом есть 2 способа:
1) Переведем время: 30 минут = 30/60 = 0,5 часа.
Найдем расстояние: 60 км/ч * 0,5 ч = 30 км.
2) Переведем скорость: 60 км/ч = 60км / 1час = 60км / 60 мин = 1км/мин.
Найдем расстояние: 1км/мин*30минут = 30 км.
Решение задач на движение в разных направлениях: сближение (встречное движение) и удаление (противоположное движение)
При встречном движении расстояние между объектами уменьшается. Объекты приближаются друг к другу со скоростью сближения.
Скорость сближения находится по формуле:
При движении в противоположных направлениях скорости объектов направлены в разные стороны. Объекты удаляются друг от друга со скоростью удаления.
Скорость удаления находится по формуле:
При решении подобных задач лучше нарисовать схему движения, чтобы было легче решать.
Задача 5. Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого велосипедиста 10 км/ч, второго — 8 км/ч. Через сколько часов они встретятся?
Решение: 1) Найдем скорость сближения: V=10+8 = 18 км/ч.
2) Найдем время: t = S:V = 36 : 18 = 2 ч.
Задача 6. Два пешехода вышли одновременно из одного и того же пункта в противоположных направлениях. Скорость первого пешехода 3км/ч, второго — 4км/ч. Какое расстояние между ними будет через 30 минут?
Решение: 1) Найдем скорость удаления пешеходов: V = 3+4=7 км/час.
2) Переведем в соответствие единицы измерения: t=30 мин = 0,5 ч.
3) Найдем расстояние: S=V × t = 7 × 0,5 = 3,5 км.
Задача 7. Два автобуса выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 300 км. Через 2 часа они встретились. Найдите второго второго автобуса, если первый ехал со скоростью 70 км/ч.
Решение. 1) Нам известно расстояние и скорость, поэтому найдем скорость по формуле: V = S:t = 300:2=150км/ч. Это скорость сближения.
2) Найдем скорость второго автобуса: 150-70 = 80км/ч.
Решение задач на движение в одном направлении: сближение и удаление
Если два объекта движутся в одном направлении и один объект “догоняет” второй, то расстояние между объектами уменьшается.
Скорость сближения при таком движении определяют по формуле:
Если два объекта движутся в одном направлении и один объект “отстает” от второго, то расстояние между объектами увеличивается.
Скорость удаления при таком движении определяют по формуле:
Если объект движется в стоячей воде (озере), то его скорость называют собственной скоростью объекта. То есть, скорость объекта равная собственной скорости объекта.
Заметим, что плот — это тело, у которого собственная скорость равна нулю (V=0). Значит, плот может плыть только по течению и со скоростью течения.
Задача 8. Расстояние между двумя автомобилями, движущимися в одном направлении, составляет 20 км. Первый автомобиль едет со скоростью 40км/ч, второй — со скоростью 30км/ч. Через сколько часов первый автомобиль догонит второй?
Решение. 1) Найдем скорость сближения автомобилей: V=40-30=10км/ч.
2) Зная расстояние (20км) и скорость сближения (10км/ч) найдем время: 20:10=2 часа.
Задача 9. Из одного населенного пункта выехали автомобиль и автобус. скорость автомобиля 70 км/ч, скорость автобуса — 50 км/ч. Какое расстояние будет между ними через 3 часа?
Решение. 1) Найдем скорость удаления : V=70-50=20км/ч.
2) Зная скорость удаления и время, найдем расстояние: S = 20*3 =60 км.
Решение задач на движение по реке
Особенностью задач на движение реке является то, что у объекта появляется дополнительная скорость — скорость течения реки. При этом возможно два варианта:
- по течению реки → скорость увеличивается;
- против течения реки → скорость уменьшается.
Таким образом, в задачах рассматривают 2 скорости:
- Скорость собственная — Vs;
- Скорость течения реки — Vt.
Задача 9. Собственная скорость лодки составляет 12 км/ч. Скорость течения реки равна 3 км/ч. Какое расстояние проплывёт лодка через 3 часа, если она плывёт по течению реки?
Решение. 1) Найдем скорость лодки. Так как она плывет по течению реки, ее скорость увеличивается.
V = Vs+ Vt = 12+3 =15км/ч.
2) Найдем расстояние: S=V×t = 15×3=45км.
Задача 10. Собственная скорость катера составляет 30 км/ч. Скорость течения реки равна 4 км/ч. Какое расстояние преодолеет катер через 4 часа, если он плывёт против течения реки?
Решение. 1) Найдем скорость. Так как катер плывет против течения реки, его скорость уменьшится.
V = Vs- Vt = 30-4 =26 км/ч.
2) Найдем расстояние: S=V×t = 26 * 4 = 104 км.
Задача 10. Скорость лодки равна 10 км/ч. При этом надо успеть проплыть 25 км за 2 часа по течению реки. Какой должна быть скорость течения реки, чтобы успеть в срок?
Решение. 1) Найдем нужную скорость: V=S:t = 25:2=12,5 км/ч.
2) Найдем скорость, которую нужно прибавить до нужно (скорость течения реки): 12,5-10=2,5км/ч.
Задача 11. Уровень ЕГЭ.
Катер прошёл по течению реки 120 км и вернулся обратно. Известно, что обратный путь занял на 1 час больше времени, а скорость катера в неподвижной воде равна 27 км/ч. Найдите скорость течения.
Решение: Пусть Vt — cкорость течения реки, тогда:
1) В одну сторону: 27+Vt – скорость перемещения катера по течению, S=120км.
2) В обратную сторону: 27-Vt – скорость перемещения катера против течения, S=120км.
Выразим время:
1) В одну сторону: t=S:V = 120:(27+Vt) – время, затраченное катером на перемещение по течению,
2) В обратную сторону: t=S:V = 120:(27-Vt) – время, затраченное катером на перемещение против течения.
Так как время перемещения против течения на час больше, чем время по течению, то:
120:(27+Vt) +1 = 120:(27-Vt).
Далее решаем уравнение и получаем ответ 3 км/ч.
Больше задач на движение Ваш ребёнок может решить, скачав программы:
Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.
Полезные советы для решения задач на движения
- В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
- Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.
- При решении задач на движение рисуйте картинки. Особенно, когда текст задачи большой и сразу в голове не укладывается. Чаще всего это нужно делать в задачах, где кто-то кого-то догоняет, встречается, или перемещается между пунктами А и В туда и обратно. На картинке сразу видно, какие отрезки пути можно просчитать. Картинка облегчает составление математической модели.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.