Как найти скорость произвольной точки

Содержание:

1. Определение скорости
2. Определение ускорения
3. Пример с решением №1.
4. Пример с решением №2.
5. Определение траектории, скорости и ускорения точки при векторном способе задания движения
6. Определение траектории, скорости и ускорения точки при координатном способе задания движения
7. Пример с решением №3.
8. Пример с решением №4.
9. Пример с решением №4.
10. Определение скорости и ускорения точки при естественном способе задания движения

Определение скорости

Вспомним основную формулу кинематики для определения скорости

Здесь – вектор перемещения точки, – время перемещения (рис. 86). Обозначим перемещение вдоль траектории за этот же промежуток времени и представим правую часть этого равенства в виде произведения двух пределов:

Первый из этих пределов равен производной и может быть вычислен, поскольку закон движения по траектории при естественном способе описания движения задается. Далее, простые рассуждения показывают, что второй предел равен по модулю единице (как предел отношения длины хорды к длине дуги) и направлен по касательной в сторону возрастания Следовательно, он определяет орт касательной для которого попутно получаем формулу

Таким образом, при естественном способе задания движения скорость точки определяется формулой

Формулу можно рассматривать как результат разложения вектора на составляющие по естественному координатному базису. Величина равна проекции скорости на направление касательной, а проекции скорости на главную нормаль и бинормаль равны нулю. В общем случае где – модуль скорости. Если точка движется в положительном направлении, то и можно записать

Определение ускорения

Будем исходить из общей формулы для ускорения

Пусть, для определенности, точка движется в положительную сторону отсчета дуг; тогда вектор скорости выражается формулой

где – модуль скорости, – орт касательной. В общем случае криволинейного движения переменны оба сомножителя в этой формуле; последний – вследствие изменения направления касательной. Поэтому орт имеет производную по времени, которая выражается формулой

где и – соответственно орт главной нормали и радиус кривизны траектории в рассматриваемом положении движущейся точки.*

Возможно вам будут полезны данные страницы:

Дифференцируя по времени выражение для скорости, получим

Формула выражает ускорение точки в виде суммы составляющих по осям естественной системы координат. Из нее следует, что ускорение имеет на эти оси проекции

Первая из них есть проекция ускорения на касательную и называется касательным ускорением. Вектор касательного ускорения

направлен в сторону скорости, если движение ускоренное и против скорости, если движение замедленное

Проекция ускорения на главную нормаль называется нормальным ускорением. Модуль и вектор нормального ускорения выражаются формулами

Так как величина положительна, нормальное ускорение всегда направлено в сторону орта то есть по главной нормали в сторону вогнутости траектории.

Проекция ускорения на бинормаль (аь) равна нулю, что означает, что вектор ускорения лежит в соприкасающейся плоскости. Таким образом, ускорение при естественном способе задания движения точки определяется как сумма касательного и нормального ускорений:

Это правило дополнительно проиллюстрировано на рис. 87, где случай а) соответствует ускоренному движению точки, а случай б) – замедленному движению. Модуль ускорения в обоих случаях определяется по теореме Пифагора:

Если точка движется прямолинейно, то нормальное ускорение не и ускорение состоит только из касательного:

При равномерном криволинейном движении наоборот, отсутствует касательное ускорение и полное ускорение точки равно ее нормальному ускорению:

Пример с решением №1.

Точка движется по окружности радиуса согласно закону Вычислить и построить скорость и ускорение точки в момент когда она пройдет половину окружности.

В момент дуговая координата точки равна половине длины окружности: откуда находим

Определяем скорость точки в момент ив расчетный момент

Определяем касательное ускорение

Видно, что оно не изменяется с течением времени – точка движется равноускоренно. Это же значение касательное ускорение имеет и в расчетный момент:

Определяем нормальное ускорение

Определяем полное ускорение в момент

На рис. 88 показаны положения точки в текущий и расчетный моменты времени, а также векторы скорости и ускорений точки в момент

В заключение заметим, что от одногоспособа задания движения можно перейти к другим способам. Например, при определении скорости в случае координатного способа описания движения был предварительно сделан переход к векторному способу в виде

• Чтобы перейти от координатного способа к естественному, прежде всего требуется найти уравнение траектории. Как было показано выше, это делается исключением из уравнений движения времени Закон движения по траектории можно получить на основе равенств

и

определяющих скорость точки при естественном и координатном способах задания движения. Приравняв правые части равенств, разрешая полученное соотношение относительно и интегрируя, находим

Это выражение определяет закон движения по траектории в общем

виде.

Если отсчет дуговой координаты вести от начального положения точки в сторону движения, то радикал положителен, и закон движения примет вид

Различают векторный, координатный и естественный (натуральный) способы задания движения.

Векторный способ задания движения состоит в следующем.

Пусть – движущаяся точка, – тело отсчета (рис. 72). Выберем в теле произвольную точку – точку отсчета, построим вектор Этот вектор, начало которого совпадает с точкой отсчета , а конец – с точкой называется радиусом-вектором точки При движении точки радиус-вектор непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени

Если эта функция известна, то для каждого момента времени может быть построен вектор и тем самым найдено положение движущейся точки в этот момент.

Функция (1) называется векторным законом (векторным уравнением) движения точки

При координатном способе задания движения с телом отсчета связывается какая-либо, например декартова прямоугольная, система координат (рис. 73). Движение точки будет задано, если ее координаты будут известны как функции времени

Зависимости (2), выражающие текущие координаты движущейся точки в виде функций времени, называются уравнениями движения точки в декартовых координатах.

Если точка движется, оставаясь все время в одной плоскости, то оси можно расположить в той же плоскости и ограничиться двумя уравнениями движения

При движении в плоскости часто удобно пользоваться полярной системой координат, задавая положение точки ее полярным углом и полярным радиусом (рис. 74). В этом случае уравнения движения точки имеют вид

Линия, описываемая движущейся точкой в пространстве, называется траекторией точки. Естественный способ задания движения состоит в задании траектории точки и закона движения по траектории.

Пусть траектория точки суть заданная кривая, – положение точки на ней (рис. 75). Будем рассматривать траекторию как криволинейную координатную ось, для чего выберем на ней начало отсчета дуг (точку ) и направление отсчета дуг (на рис. 75 направление отсчета дуг выбрано вправо от точки ). Длина дуги взятая со знаком плюс или минус в зависимости от положения точки относительно начала отсчета дуг вполне определяет положение точки в пространстве и называется дуговой координатой точки. Движение точки будет задано, если ее дуговая координата будет выражена в виде функции времени

Зависимость (4) называется законом движения точки по траектории или, что то же самое, законом движения точки в естественной форме.

Пример с решением №2.

Написать уравнения движения точки, движущейся равномерно по окружности радиуса и делающей оборотов за одну минуту.

Начнем с естественного способа описания движения. Изображаем траекторию- окружность радиуса с центром в точке (рис. 76). Начало отсчета дуг совместим с положением точки в момент начала наблюдения, то есть при за положительное направление отсчета выберем направление в сторону движения точки.

Пусть – положение движущейся точки в текущий момент времени Для центрального угла который будем отсчитывать в сторону движения точки, согласно условию, можем написать

Здесь измеряется в радианах, – в секундах.

Длина дуги радиус окружности и центральный угол связаны геометрическим соотношением

Подставляя сюда найденное значение получаем

Это и есть естественной форме.

Для описания движения в координатной форме прежде всего следует выбрать подходящую систему координат, например, изображенную на рис. 77. Далее строят координатные отрезки и определяют соответствующие переменные расстояния. В нашем случае будем иметь:

Подставляя сюда угол как функцию времени, получаем уравнения движения в координатной форме

Пусть – координатные орты. Тогда для радиуса-вектора точки будем иметь:

Полученное равенство, выражающее радиус-вектор точки как функцию времени, служит векторным уравнением ее движения.

Определение траектории, скорости и ускорения точки при векторном способе задания движения

Пусть движение точки задано векторным способом, то есть задан радиус-вектор точки как функция времени

Линия, описываемая концом переменного вектора, начало которого находится в заданной неподвижной точке, называется годографом этого вектора. Отсюда и из определения траектории следует правило: траектория точки есть годограф ее радиуса-вектора.

Пусть в некоторый момент точка занимает положение и имеет радиус-вектор а в момент – положение и радиус-вектор (рис. 78).

Вектор соединяющий последовательные положения точки в указанные моменты, называется вектором перемещения точки за время Вектор перемещения следующим образом выражается через значения вектор-функции (5):

Если вектор перемещения поделить на величину промежутка получим вектор средней скорости точки за время

Будем теперь уменьшать промежуток устремляя его к нулю. Предел, к которому стремится вектор средней скорости при неограниченном уменьшении промежутка называется скоростью точки в момент или просто скоростью точки В соответствии со сказанным для скорости получаем:

Итак, вектор скорости точки равен производной по времени от ее радиуса-вектора:

Поскольку секущая в пределе (при ) переходит в касательную приходим к выводу, что вектор скорости направлен по касательной к траектории в сторону движения точки.

В общем случае скорость точки также переменна, и можно интересоваться быстротой изменения скорости. Скорость изменения скорости называется ускорением точки.

Для определения ускорения выберем какую-либо неподвижную точку и будем откладывать из нее вектор скорости в различные моменты времени. Линия, которую опишет конец вектора скорости, представляет собой годограф Годограф и скорости (рис. 79). Изменение вектора скорости выражается в том, что геометрическая точка движется по годографу скорости, а скорость этого движения служит, по определению, ускорением точки

Применив для переменного вектора все те рассуждения, которые были использованы выше для переменного вектора для ускорения получаем:

или, при обозначении производной по времени точкой:

Формулы (6) – (8) являются наиболее общими формулами кинематики для определения скорости и ускорения.

Определение траектории, скорости и ускорения точки при координатном способе задания движения

Пусть движение точки задано уравнениями движения в декартовых координатах:

Для каждого момента времени по этим уравнениям можно определить координаты точки в этот момент и указать ее положение в пространстве. Придавая всевозможные значения, получим множество положений движущейся точки в пространстве – ее траекторию. Следовательно, уравнения движения одновременно являются уравнениями траектории точки в параметрической форме, причем параметром служит время . Чтобы получить уравнение траектории в виде зависимости между координатами точки, достаточно из уравнений движения исключить время.

Пример с решением №3.

Движение точки задано уравнениями ( – в сантиметрах, – в секундах). Найти уравнение траектории точки в координатной форме.

Для определения уравнения траектории из уравнений движения исключаем время Для этого из первого уравнения выражаем

и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:

Опуская промежуточные выражения, получаем уравнение траектории

Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке Траекторией служит кусок этой параболы, заключенный между точками с координатами и (рис. 80).

Пример с решением №4.

Определить уравнение траектории, если точка движется согласно уравнениям (– в сантиметрах, – в секундах):

Для исключения времени из уравнений движения выразим из этих уравнений и

Возводя эти равенства в квадрат и почленно складывая, получаем уравнение траектории в координатной форме:

Это уравнение эллипса с центром в точке и с полуосями (рис. 81). Траекторией служит вся кривая эллипса.

Займемся теперь определением скорости и ускорения.

Зная уравнения движения точки, можно выразить в функции времени радиус-вектор точки (рис. 82):

Теперь находим скорость, дифференцируя радиус-вектор по времени:

При дифференцировании учитывается, что оси неподвижны, поэтому координатные орты являются постоянными векторами, и их производные равны нулю.

Полученная формула определяет скорость точки в виде разложения

по координатному базису Так как коэффициенты при ортах равны проекциям скорости на соответствующие координатные оси, отсюда следуют формулы

По известным проекциям находим модуль и направляющие косинусы скорости:

Аналогичным образом определяется и ускорение. Дифференцируя выражение для вектора скорости, получаем:

Откуда для проекций ускорения следуют формулы

Проекции ускорения можно выразить также через проекции скорости:

Модуль и направляющие косинусы ускорения выражаются равенствами

Пример с решением №4.

Точка движется в плоскости ху согласно уравнениям

где – заданы в сантиметрах, время – в секундах, а величины – заданные постоянные. Найти скорость и ускорение точки в момент, когда она впервые после начала движения пересекает ось

Скорость и ускорение находим, вычисляя их проекции на координатные оси. Сначала это сделаем для произвольного момента

Когда точка находится на оси , выполняется равенство Подставляя это значение во второе уравнение движения и решая полученное уравнение относительно находим

Момент соответствует началу движения, а первое после начала движения пересечение оси происходит при Подставляя это значение в предыдущие формулы, найдем

Таким образом, в расчетный момент времени скорость ускорение имеют модули

и направляющие косинусы

На рис. 83 показана геометрическая картина движения. Траекторией точки служит окружность радиуса с центром в точке Подставляя в уравнения движения находим, что в начальный момент точка находится в положении Придавая времени малое положительное значение и определяя знаки координат получаем из чего следует, что точка движется из положения против хода часовой стрелки. В расчетный момент она находится в начале координат, имея скорость и ускорение

Определение скорости и ускорения точки при естественном способе задания движения

Естественные координатные оси и их орты

Пусть заданы траектория точки, начало и направление отсчета дуг. Выберем на траектории произвольным образом точку и проведем касательную . Плоскость, проходящая через точку перпендикулярно к касательной называется нормальной плоскостью траектории в точке (рис. 84).

Придадим дуговой координате приращение и отметим точку с координатой Пусть – касательная к траектории в точке В общем случае траектория точки – пространственная кривая, поэтому касательные и суть скрещивающиеся прямые.

Проведем прямую параллельную касательной Прямые и образуют плоскость Предельное положение плоскости когда точка ‘ неограниченно приближается к точке называется соприкасающейся плоскостью траектории в точке Соприкасающаяся плоскость представляет собой ту из бесконечного множества плоскостей, проходящих через касательную которая наиболее тесно примыкает к траектории в окрестности точки В случае плоской траектории соприкасающаяся плоскость совпадает с плоскостью траектории.

Нормальная и соприкасающаяся плоскости взаимно перпендикулярны. Проведем через точку третью плоскость, перпендикулярную к обеим указанным плоскостям – так называемую спрямляющую плоскость. В итоге получаем прямой трехгранный угол с вершиной в точке называемый естественным трехгранником траектории в этой точке. Ребрами естественного трехгранника являются касательная главная нормаль – линия пересечения нормальной и соприкасающейся плоскостей и бинормаль (вторая нормаль) – линия пересечения нормальной и спрямляющей плоскостей (рис. 85).

Касательная, главная нормаль и бинормаль взаимно перпендикулярны и после установления на них направлений образуют естественную систему координатных осей. Положительное направление касательной выбирается в сторону возрастания дуговой координаты и задается ортом касательной Положительное направление главной нормали задается ортом который направляют от точки в сторону вогнутости траектории. Орт бинормали выбирают согласно правилу чем обеспечивается правосторонность естественного координатного базиса (см. рис. 85).

Определение линейных скоростей и ускорений точек вращающегося тела

Рассмотрим
точку M,
тела, совершающего вращательное движение
по закону
относительно оси, проходящей через
точку O.
Точка расположена на расстоянии R
от оси вращения. Дуговая координата s
точки, измеряемая от положения O₁,
определяется выражением

.
(37)

Тогда
скорость точки M
найдем в соответствии с уравнением
(12),
полученным для естественного способа
задания движения

Скорость
точки тела, совершающего вращательное
движение, определяется как произведение
угловой скорости на расстояние точки
до оси вращения

.

(38)

Направлен
вектор скорости по направлению вращения.

Для
нахождения ускорения точки воспользуемся
выражениями (23)
и (25),
подставив в них (38)

,

.

Касательное
ускорение определяется, как произведение
углового ускорения на расстояние до
оси, и направлено по направлению углового
ускорения.

Нормальное
ускорение определяется как произведение
квадрата угловой скорости на расстояние
до оси вращения. Направлено нормальное
ускорение всегда к оси вращения.

(39)

Отклонение
вектора полного ускорения от радиуса
определяется следующим образом

.
(40)

Плоское движение твердого тела

Плоским
(плоскопараллельным)
называется движение твердого тела, при
котором все его точки описывают плоские
траектории параллельные базовой
плоскости.

Пусть
тело совершает плоское движение по
отношению к некоторой базовой плоскости.
Все точки, лежащие на перпендикуляреAB
к базовой плоскости, движутся одинаково.
Следовательно, для задания плоского
движения твердого тела необходимо и
достаточно задать движение какого-нибудь
сечения тела.

.
(41)

Система
(41)
представляет собой уравнения плоского
движения твердого тела. Первые два
уравнения описывают движение некоторой
точки сечения, а третье – вращение тела
по отношению к этой точке.

Точка,
выбранная для определения положения
сечения, называетсяполюсом.

Таким
образом, плоское движение твердого тела
складывается из поступательного
движения, при котором все точки тела
движутся так же, как полюс, и из
вращательного движения вокруг этого
полюса.

Основными
кинематическими характеристиками
плоского движения являются скорость и
ускорение поступательного движения,
равные скорости и ускорению полюса, а
также угловая скорость и угловое
ускорение вращательного движения вокруг
полюса. Причем, вращательная составляющая
движения от выбора полюса не зависит.

Определение скоростей точек тела при плоском движении

Рассмотрим
сечение тела, совершающего плоское
движение. Пусть есть некоторая точкаA,
движение которой известно. Выберем ее
в качестве полюса. Необходимо найти
скорость произвольной точки M
этого сечения.

Воспользуемся
векторным способом задания движения.
Из рисунка видно, что

.

Возьмем
производную от этого выражения

.

Так
как
в итоге получим

.
(42)

где
– относительная скорость точкиM
при вращении тела относительно полюса
A,
определяется как произведение угловой
скорости тела на расстояние от точки
до полюса

.

Таким образом,
скорость любой точки тела при его плоском
движении равна геометрической сумме
скорости полюса и скорости точки в ее
вращении вместе с полюсом по отношению
к полюсу.

Модуль
и направление вектора скорости точки
находится по правилу параллелограмма.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #

  02.04.2015390.66 Кб2316.doc

• #
• #
• #
• #
• #
• #
• #
• #
• #

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Скоростью точки называют кинематическую меру ее движения, равную производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета.

Скорость относительно выбранной системы отсчета это одна из основных характеристик движения точки.

Вектор скорости направлен по касательной к траектории точки в сторону движения.

Рассмотрим перемещение точки за малый промежуток времени Δt:

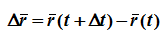
тогда

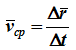
средняя скорость точки за промежуток времени Dt.

Наш видеоурок по теме:

Другие видео

Скорость точки в данный момент времени

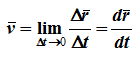
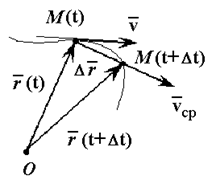
Скорость точки при векторном способе задания движения

Положение движущейся точки М относительно системы отсчета в момент времени t₁ определяется радиус-вектором r.

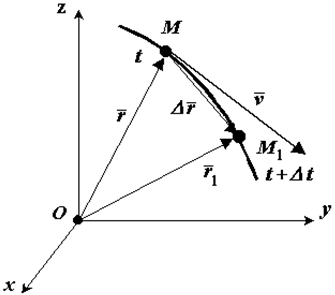
Рис. 1

В другой момент времени t₁=t+Δt точка займет положение М₁ с радиус-вектором r₁.

За время Δt радиус-вектор движущейся точки изменится на

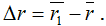
Средней скоростью v_ср называется отношение изменения радиус-вектора Δr к изменению времени Δt.

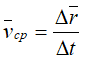
Скорость точки равна первой производной по времени от ее радиус-вектора.

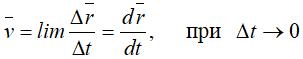
Скорость точки при координатном способе задания движения

Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим

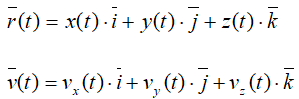
После дифференцирования

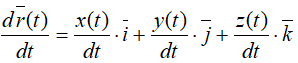
Отсюда следует

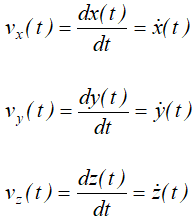
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.

Модуль скорости и направляющие косинусы равны:

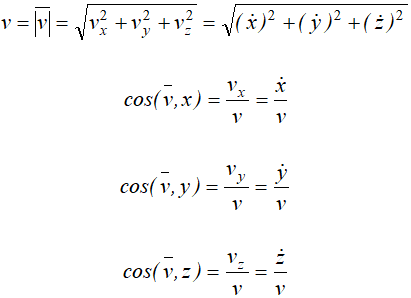
Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:

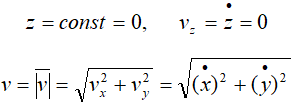
Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда

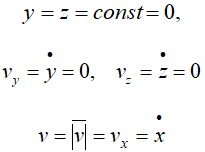
Скорость точки при естественном способе задания движения

Пусть скорость точки задана естественным способом, т.е. заданы траектория точки и закон ее движения по траектории s=f(t).

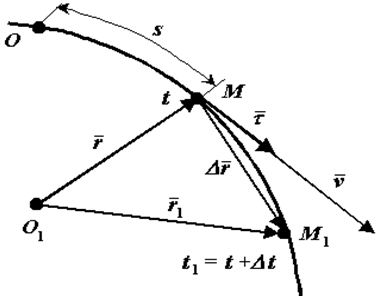
Рис. 2

Вычислим скорость точки. Используем радиус-вектор r. движущейся точки, начало которого находится в неподвижной точке O₁

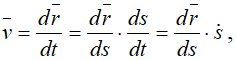
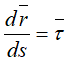
— единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.

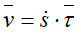
При ds>0 направления векторов τ и dr совпадают.

Если точка движется в сторону убывающих расстояний, то ds<0 и направления векторов τ и dr противоположны.

При

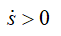
вектор скорости направлен по τ, т.е. в сторону возрастающих расстояний;

при

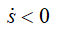
он имеет направление, противоположное τ, т.е. в сторону убывающих расстояний.

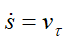
— алгебраическая скорость точки, проекция скорости v на положительное направление касательной к траектории.

Естественное задание движения точки полностью определяет скорость по величине и направлению.

Примеры решения задач >
Ускорение точки >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее