Порядок выполнения работы
1.Измерить на весах массы пуль (масса цилиндра и длина нитей маятника указаны на установке).
2.Отрегулировать длину нитей так, чтобы геометрическая ось маятника была направлена горизонтально (параллельно стволу пушки).
3.Установить шкалу, предназначенную для определения отклонения маятника, параллельно оси маятника вблизи визира маятника.
4.Сжать пружину пушки и зафиксировать штифтом ее положение. Вставить пулю в дуло пушки и дослать ее шомполом до упора.
5.Поднятием штифта произвести выстрел и снять отсчет максимального отклонения S0 маятника по шкале.
6.Повторить измерения не менее пяти раз.
7.Провести измерения для всех пуль.
8.Вычислить скорость пули при каждом выстреле по рабочей фор-
муле (16).
9.Для каждой пули найти среднее значение скорости пули и среднюю абсолютную погрешность измерения.
10.Занести в таблицу для каждой пули данные наблюдений и расчетов.
|
№ |
m, г |
S0, мм |
υ, м/с |
υ , м/с |
|Δ υ |, м/с |
|Δ υ |, м/с |
|
опыта |
||||||
|
1 |
||||||
|
2 |
||||||
|
3 |
||||||
|
4 |
||||||
|
5 |
11. Подсчитать максимальную относительную погрешность метода измерений по формуле
|
Δυ |
M |
m |
1 1 |
S0 |
1 |
g |
1 |
, |
(17) |
|||||||||||||||
|
υ |
M m |
M m m |
S0 |
2 |
g |
2 |
||||||||||||||||||
где в качестве погрешностей измерений m, S0 следует подставлять погрешности соответствующих измерительных средств. В качестве погрешностей табличных величин M, g, ℓ принимается единица последнего разряда в численном значении. Из формулы (17) определить максимальную абсолютную погрешность метода:
|
Δυ |
Δυ |
υ . |
||||
|
υ |
||||||
Сравнить полученный результат со средней абсолютной погрешностью из п. 9.
11
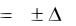
12. Окончательный результат для каждой пули записать в виде
где |Δυ| – наибольшее значение абсолютной погрешности.
Указания по технике безопасности
Запрещается производить выстрел без предварительной проверки направленности ствола пушки вдоль геометрической оси мишени.
Контрольные вопросы
1.Определите понятия импульса тела, импульса системы тел.
2.Какая система тел называется замкнутой или изолированной?
3.Показать, что внутренние силы не изменяют импульс системы тел. Чем определяется изменение импульса системы?
4.Сформулируйте законы сохранения импульса и механической энергии.
5.Определите понятия центрального, абсолютно упругого, абсолютно неупругого ударов на примере столкновения шаров.
6.В чем заключается баллистический метод измерения скорости полета пули?
7.В каком случае систему маятник–пуля можно считать замкнутой?
8.При каких условиях в баллистическом методе для расчѐта скорости пули можно использовать закон сохранения импульса вместо закона сохранения момента импульса?
9.Определить долю кинетической энергии пули, перешедшей во внутреннюю энергию системы маятник–пуля после неупругого удара.
10.Как определяется максимальная относительная погрешность метода измерений?
11.Какими факторами ограничивается точность измерения скорости полета пули в опыте?
12
Список рекомендуемой литературы
Сивухин, Д. В. Общий курс физики : учеб. пособие для вузов : в 5 т. Т. 1. Механика / Д. В. Сивухин. М. : Физматлит, 2010. 560 с. (см. § 10,
с. 73–76 ; § 26, с. 151–155 ; § 28, с. 157–165).
Удар твердых тел : Физический энциклопедический словарь : в 5 т. Т. 5. М. : Сов. энцикл., 1983.
Физический практикум. Механика и молекулярная физика / под ред. В. И. Ивероновой. М. : Наука, 1967. 352 с. (см. задачу 19).
13
П Р И Л О Ж Е Н И Я
Приложение 1
Расчѐт доли кинетической энергии пули, перешедшей во внутреннюю энергию системы
При абсолютно неупругом ударе пули и маятника часть кинетической энергии пули переходит во внутреннюю энергию системы маятник– пуля (9). Кинетическая энергия этой системы до удара равна кинетической
|
энергии пули |
mυ2 |
, а сразу после удара – |
(M m)u 2 |
. Во внутреннюю |
|||||||
|
2 |
2 |
||||||||||
|
энергию переходит разность этих энергий: |
|||||||||||
|
mυ2 |
(M m)u 2 |
M mυ2 |
. |
||||||||
|
2 |
2 |
M |
m |
2 |
|||||||
Следовательно, во внутреннюю энергию переходит доля кинетической энергии пули, равная
|
M |
1 |
||||
|
. |
|||||
|
M m |
1 |
m |
|||
|
M |
|||||
При m << M почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M во внутреннюю энергию переходит половина первоначальной кинетической энергии.
Приложение 2
Абсолютно упругий удар
Абсолютно упругим ударом называется удар, при котором механическая энергия тел не переходит в другие виды энергии. При таком ударе на первой стадии кинетическая энергия полностью или частично переходит в потенциальную энергию упругой деформации. Во время сближения шаров силы, действующие на них, увеличиваются пропорционально деформации в соответствии с законом Гука. Скорости обоих шаров становятся одинаковыми в момент их максимальной деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга, а потенциальная энергия переходит в кинетическую. Тела разлетаются со скоростями, величины и направления которых зависят от законов сохранения полной механической энергии и импульса системы тел.
14
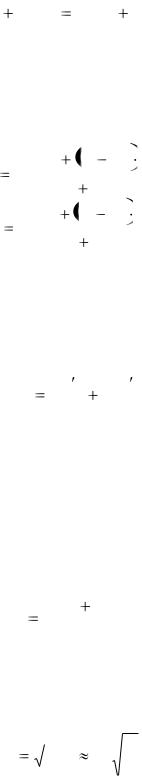
Хорошим примером абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.
При абсолютно упругом ударе выполняются и закон сохранения импульса и закон сохранения механической энергии:
|
m1υ1+ m2υ2 = m1u1+ m2u2, |
|||||||||||
|
m υ2 |
m υ2 |
m u2 |
m u2 |
(П. 1) |
|||||||
|
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
, |
|||
|
2 |
2 |
2 |
2 |
||||||||
где m1, m2 – массы сталкивающихся шаров; υ1, υ2 – скорости шаров до столкновения; u1, u2 – скорости шаров после столкновения.
Решая систему уравнений (П. 1), получим:
|
u1 |
2m2υ2 |
m1 m2 υ1 , |
|||
|
m1 |
m2 |
||||
|
u2 |
2m1υ1 m2 m1 υ2 . |
||||
|
m1 |
m2 |
||||
При абсолютно упругом ударе пули о маятник выполняются законы сохранения импульса и механической энергии:
|
mυ = mυ′+ MV′, |
||||||
|
mυ2 |
mυ 2 |
MV |
2 |
. |
||
|
2 |
2 |
2 |
||||
где υ – скорость пули до удара; υ‘ – скорость пули после удара; V‘ – скорость маятника после удара.
Из этих соотношений в проекции на горизонтальное направление получаем, что импульс, приобретаемый маятником при таком ударе, равен
MV′ = m(2υ – V′),
откуда
|
υ |
1 |
M m |
V’ . |
(П. 2) |
|
|
2 m |
Из закона сохранения энергии маятника после удара начальная скорость маятника равна
|
S0‘ |
g |
, |
(П. 3) |
|||
|
V’ |
2gh |
|||||
15

где S0‘ – баллистический отброс в случае абсолютно упругого удара. Подставляя выражение (П. 3) в (П. 2), получим:
|
1 |
M |
m |
M |
m S0‘ |
g |
. |
(П. 4) |
|||||||
|
υ |
2gh |
|||||||||||||
|
2 |
m |
m |
2 |
|||||||||||
Из соотношений (П. 2) и (П. 4) следует, что при абсолютно упругом ударе скорость маятника
|
V’ |
2υ |
m |
||||||||
|
M |
m |
|||||||||
|
и баллистический отброс, |
||||||||||
|
S0‘ |
2υ |
m |
, |
|||||||
|
M m |
g |
|||||||||
в два раза больше, чем при абсолютно неупругом ударе.
Приложение 3
Пропорциональность максимального отклонения маятника импульсу силы при баллистическом методе измерения
После удара при малом угле отклонения маятник продолжает свое движение по гармоническому закону
2
S Ssin t,
0 T
где S0 – максимальное отклонение маятника от положения равновесия (амплитуда колебания); Т – период колебания,
T 2 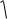
 g.
g.
Мгновенное ut и максимальное umax значения скорости маятника соответственно запишутся следующими соотношениями:
|
ut |
dS |
2π |
S0 cos |
2π |
t |
, |
||||||
|
dt |
||||||||||||
|
T |
T |
(П. 5) |
||||||||||
|
um ax |
2π |
S0 S0 |
g |
. |
||||||||
|
T |
||||||||||||
16

Импульс ударной силы равен изменению импульса маятника:
0
где u – начальная скорость маятника с пулей сразу после удара.
Скорость маятника u сразу после удара будет практически равна максимальной скорости umax, с которой маятник должен проходить положение равновесия при гармонических колебаниях.
Подставляя в (П. 6) выражение для скорости umax из (П. 5), получим:
|
FdtMS |
g |
(П. 7) |
||
|
0 . |
||||
|
0 |
||||
Из последнего равенства видно, что максимальное отклонение маятника S0 пропорционально импульсу ударной силы. Это свойство метода измерения очень ценно на практике.
Соотношение (П. 6) лежит в основе баллистического метода измерения.
Приложение 4
Удар пули и маятника в общем случае
В общем случае при ударе пули и физического маятника при решении задачи необходимо пользоваться законом сохранения момента импульса. В нашем случае, когда баллистический маятник можно рассматривать как математический (размеры маятника малы по сравнению с длиной нитей подвеса), возможно использование закона сохранения импульса. Действительно, закон сохранения момента импульса для системы маятник– пуля можно записать в следующем виде:
где mυℓ – момент импульса пули до удара; ℓ – расстояние от центра тяжести системы маятник–пуля до точки подвеса (см. рис. 3); J – момент инерции маятника с пулей относительно оси вращения АА‘; J – момент им-
|
пульса системы маятник–пуля после удара; ω |
u |
– угловая скорость. |
|
Так как размеры маятника малы по сравнению с длиной нити подвеса, то его момент инерции можно определить как момент инерции материальной точки:
J(M m) 2
.
17
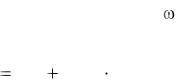
Подставляя выражения для угловой скорости и момента инерции J маятника с пулей в (П. 8), получим:
|
mυ |
(M m) 2 |
u |
. |
После преобразований последнее выражение принимает вид закона сохранения импульса для случая абсолютно неупругого удара:
Mυ = (M+m)u.
18
|
СОДЕРЖАНИЕ |
|
|
Лабораторная работа |
|
|
Измерение скорости полета пули методом баллистического |
|
|
маятника…………………………………………………………………………… |
3 |
|
Теоретические замечания……………………………………………………… |
3 |
|
Оборудование……………..…………………………………………………….. |
10 |
Описание установки……………………………………………..………… 10
Порядок выполнения работы………………………………..……………… 11 Указания по технике безопасности………………………………………… 12
Контрольные вопросы…………………………………………..…………. 12
Список рекомендуемой литературы……………………………….….… 13
Приложение 1. Расчѐт доли кинетической энергии пули, перешедшей во внутреннюю энергию системы………………………… 14
Приложение 2. Абсолютно упругий удар.………………………………… 14
Приложение 3. Пропорциональность максимального отклонения маятника импульсу силы при баллистическом методе измерения…………. 16
Приложение 4. Удар пули и маятника в общем случае ………………… 17
19
Учебное издание
ФИЗИЧЕСКИЙ ПРАКТИКУМ Измерение скорости полета пули методом баллистического маятника
Учебно-методическое пособие для студентов естественных факультетов
С о с т а в и т е л и :
Страхова Людмила Львовна, Хвалин Александр Львович, Сотов Леонид Сергеевич
Под редакцией профессора А. А. Игнатьева
Редактор И. Ю. Бучко Технический редактор В. В. Володина
Корректор Е. Б. Крылова Оригинал-макет подготовили О. Г. Данке, Т. Н. Сиротинина
___________________________________________________________________
Подписано в печать 05.06.2012. Формат 60 84 1/16.
Усл. печ. л. 1,16 (1,25). Тираж 100. Заказ 37.
___________________________________________________________________
Издательство Саратовского университета. 410012, Саратов, Астраханская, 83.
Типография Издательства Саратовского университета. 410012, Саратов, Астраханская, 83.
20
Условие задачи:
В покоящийся шар массой 1 кг, подвешенный на стержне, попадает пуля массой 0,01 кг, летящая под углом 45° к стержню, и застревает в нем. После удара пуля с шаром откачнулись на высоту 0,02 м. Найти скорость пули.
Задача №2.10.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(M=1) кг, (m=0,01) кг, (alpha=45^circ), (h=0,02) м, (upsilon-?)
Решение задачи:
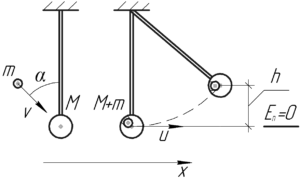 Так как пуля застревает в шаре, то в данном случае мы имеем дело с абсолютно неупругим ударом. Вдоль горизонтальной оси на шар и пулю не действуют никакие силы, то есть система из этих тел замкнута вдоль этой оси. Запишем закон сохранения импульса до и после удара в проекции на эту ось:
Так как пуля застревает в шаре, то в данном случае мы имеем дело с абсолютно неупругим ударом. Вдоль горизонтальной оси на шар и пулю не действуют никакие силы, то есть система из этих тел замкнута вдоль этой оси. Запишем закон сохранения импульса до и после удара в проекции на эту ось:
[mupsilon cdot sin alpha = left( {m + M} right)u]
Выразим скорость пули (u) до удара:
[upsilon = frac{{left( {m + M} right)u}}{{msin alpha }};;;;(1)]
После удара шар начнет двигаться и вскоре достигнет максимальной высоты (h). По закону сохранения энергии:
[frac{{left( {M + m} right){u^2}}}{2} = left( {M + m} right)gh]
Откуда скорость шара (u) с застрявшей в нём после удара пулей равна:
[u = sqrt {2gh} ;;;;(2)]
Подставим (2) в (1), так мы получим решение этой задачи в общем виде.
[upsilon = frac{{left( {m + M} right)sqrt {2gh} }}{{msin alpha }}]
Все данные задачи известны и даны в системе СИ, можем приступать к расчету ответа:
[upsilon = frac{{left( {0,01 + 1} right)sqrt {2 cdot 10 cdot 0,02} }}{{0,01 cdot sin 45^circ }} = 90,34; м/с = 325,21; км/ч]
Ответ: 325,21 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.24 Мальчик, стоя на Земле, бросает камень горизонтально со скоростью 5 м/с
2.10.26 Найти количество теплоты, выделившейся при абсолютно неупругом ударе свинцового
2.10.27 Два груза массами 0,04 и 0,01 кг соединены невесомой нитью, переброшенной
Решение.
Будем рассматривать движение системы «стержень – пуля»
относительно системы отсчета, начало которой расположено в центре стержня О,
а ось ![]() совпадает с осью вращения и направлена «на
совпадает с осью вращения и направлена «на
нас» (рис. 14). В момент удара на систему действуют силы тяжести
и
реакции опоры – оси. Линии действия сил реакции оси и тяжести, действующих на стержень,
и силы тяжести, действующей на пулю, проходят через центр стержня О. Таким
образом, все внешние силы являются центральными, их моменты относительно центра
О равны нулю, следовательно, при столкновении выполняется закон
сохранения момента импульса:
![]() ,
,
(1)
где
![]() и
и ![]() – моменты
– моменты
импульса системы относительно центра ![]() непосредственно до удара
непосредственно до удара
(рис. 14, а) и сразу после него (рис. 14, б) соответственно[1].
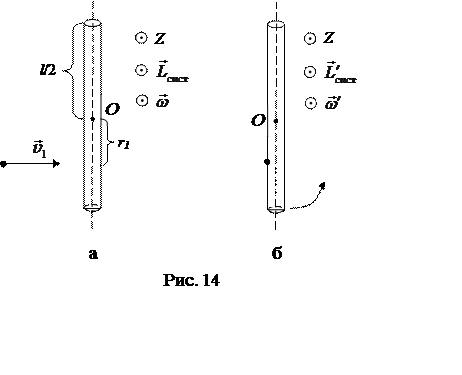 До
До
взаимодействия стержень был неподвижен, поэтому момент импульса системы равен
моменту импульса пули:
![]() , (2)
, (2)
где
![]() – момент инерции пули относительно оси
– момент инерции пули относительно оси
вращения;
![]() – угловая скорость пули непосредственно
– угловая скорость пули непосредственно
перед ударом.
Примем
пулю за материальную точку, тогда ее момент инерции относительно оси вращения
![]() .
.
(3)
Модуль
угловой скорости пули выражается через модуль линейной скорости ![]() и расстояние
и расстояние ![]() от
от
точки попадания пули до оси ![]()
![]() ,
,
(4)
где
![]()
Направление
![]() (рис. 14, а – «на нас») определяется по
(рис. 14, а – «на нас») определяется по
правилу буравчика в соответствии с направлением вращения.
После
взаимодействия пули и стержня система начинает вращение как одно целое с
угловой скоростью ![]() поэтому
поэтому
![]() ,
,
(5)
где
![]() – угловая скорость системы непосредственно
– угловая скорость системы непосредственно
после удара.
Момент
инерции стержня относительно оси вращения, которая в рассматриваемом случае
совпадает с осью симметрии стержня, определяется по формуле:
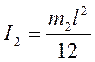 .
.
(6)
Подставив
формулы (2) и (5) в уравнение (1), получим соотношение:
![]() .
.
(7)
Отсюда
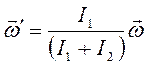 .
.
(8)
Заметим, что моменты импульса пули до и после удара можно
вычислить, основываясь на определении момента импульса материальной точки:
![]() и
и ![]() .
.
При
анализе выражения (8) можно сделать два вывода:
1)
угловая скорость системы во втором состоянии сонаправлена с угловой скоростью пули
в первом состоянии: ![]() ;
;
2)
так как моменты инерции величины положительные, модуль угловой скорости ![]() определяется по формуле:
определяется по формуле:
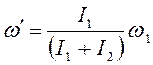 .
.
(9)
Подставим
выражения (3), (4) и (6) в равенство (9):
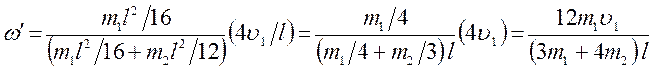 . (10)
. (10)
Подставим
данные задачи в уравнение (10) и получим:
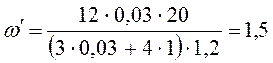 рад/с.
рад/с.
Ответ: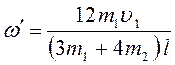 ,
, ![]() рад/с.
рад/с.
Библиографический список
1. С
а в е л ь е в И. В. Курс общей физики: В 5 кн. Кн. 1. Механика / И. В. С
а в е л ь е в. М., 1998. 336 с.
2. Я в о р с к и й Б. М. Курс физики / Б. М. Я в о
р с к и й, А. А. Д е т л а ф, Л. Б. М и л к о в с к а я. М., 2001. 718
с.
3. Т
р о ф и м о в а Т. И. Курс физики / Т. И. Т р о ф и м о в а. М., 2004. 542
с.
4. Физический
энциклопедический словарь / Под ред. А. М. Прохорова.
М., 1984. 940 с.
5.
Д ж а н к о л и Д. Физика / Д. Д ж а н к о л и. М., 1989. Т. 1. 667 с.
6.
Н и к и т и н Н. Н. Курс теоретической механики / Н. Н. Н и к и т и н. М., 1990.
607 с.
_________________________________________________
Учебное
издание
ДРОЗДОВА Илга
Анатольевна, ТОДЕР Георгий Борисович
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
(ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ)
![]() Редактор Т. С. Паршикова
Редактор Т. С. Паршикова
***
Подписано в печать . 02.2010.
Формат 60 ´ 84 1/16.
Плоская печать. Бумага офсетная. Усл.
печ. л. 2,4. Уч.-изд. л. 2,6.
Тираж 800 экз. Заказ .
**
Редакционно-издательский
отдел ОмГУПСа
Типография ОмГУПСа
*
644046, г. Омск, пр. Маркса, 35
 |
И. А.
ДРОЗДОВА, Г. Б. ТОДЕР
ЗАКОНЫ
СОХРАНЕНИЯ В МЕХАНИКЕ
(ПРИМЕРЫ
РЕШЕНИЯ ЗАДАЧ)
 ОМСК 200
ОМСК 200
9
[1] Отметим, что закон сохранения
импульса в рассматриваемых условиях не выполняется: при взаимодействии пули и
стержня со стороны оси на стержень действует сила реакции, которой нельзя
пренебречь.
2.76.
Пуля массой m = 10 г, летевшая со скоростью v = 600 м/с, попала в баллистический маятник (см. рис. ниже)
массой М = 5 кг и застряла в нем. На какую высоту h,
откачнувшись после удара, поднялся маятник?
Дано: Решение:
 m = 0,01 кг
m = 0,01 кг
v
= 600 м/с
М = 5 кг
h – ?
Ответ: 7,32∙10-2 м.
2.77. В
баллистический маятник массой М = 5 кг попала пуля массой m = 10 г и застряла в нем. Найти скорость v пули, если
маятник, отклонившись после удара, поднялся на высоту h = 10 см.
 Дано: Решение:
Дано: Решение:
М = 5 кг
m = 0,01 кг
h
= 0,1 м
v – ?
Ответ: 701 м/с .
2.78. Два
груза массами m1 = 10 кг и т2 = 15 кг подвешены на нитях длиной l = 2 м так, что грузы соприкасаются между
собой. Меньший груз был отклонен на угол φ = 60° и выпущен. Определить высоту h, на которую
поднимутся оба груза после удара. Удар грузов считать неупругим.
 Дано: Решение:
Дано: Решение:
m1 = 10 кг
т2 = 15 кг
l
= 2 м
φ = 60°
h – ?
Ответ: 0,16 м.
2.79. Два
неупругих шара массами m1 = 2 кг и т2 = 3 кг движутся со скоростями соответственно v1 = 8 м/с и v2 = 4 м/с. Определить увеличение ![]() внутренней энергии шаров при их
внутренней энергии шаров при их
столкновении в двух случаях: 1) меньший шар нагоняет больший; 2) шары движутся
навстречу друг другу.
Дано: Решение:
 m1 = 2 кг
m1 = 2 кг
т2 = 3 кг
v1 = 8 м/с
v2 = 4 м/с
![]() – ?
– ?
Ответ: 9,6 Дж , 86,4 Дж .
2.80.
Шар массой m1, летящий со
скоростью v1
= 5
м/с, ударяет неподвижный шар массой т2. Удар прямой,
неупругий. Определить скорость и шаров после удара, а также долю w кинетической энергии летящего шара, израсходованной на
увеличение внутренней энергии этих шаров. Рассмотреть два случая: 1) m1 = 2 кг, m2 = 8 кг, 2) m1 = 8 кг, m2 = 2 кг.
Дано: Решение:
 v1
v1
= 5
м/с
1) m1 = 2 кг
m2 = 8 кг
2) m1 = 8 кг
m2 = 2 кг
и –
?
w –
?
Ответ: 1 м/с , 0,8 , 4 м/с , 0,2 .
