Формула скорости волны в физике
Формула скорости волны
Определение
Фронт волны (волновая поверхность) – это геометрическое место точек среды, для которых в некоторый момент времени фаза волны
имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),]
где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).]
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right),]
где $T$ – период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны – это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
[v=sqrt{frac{K}{rho }}left(4right),]
где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
[v=sqrt{frac{gamma p}{rho }}left(5right),]
где $gamma $ – показатель адиабаты; $p$ – давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
[v=sqrt{frac{E}{rho }}left(6right),]
где $E$ – модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
[v=sqrt{frac{G}{rho }left(7right),}]
где $G$ – модуль сдвига среды; $rho $ – плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
[u=v-frac{dv}{dlambda }left(8right).]
Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Пример 1
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
[v=frac{lambda }{T} left(1.1right).]
Найдем период колебаний как время одного полного колебания:
[T=frac{t}{N} left(1.2right).]
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.]
Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).]
Ответ. $v=5frac{м}{с}$
Пример 2
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?
Решение. Фазовую скорость движения волны найдем как:
[v=frac{lambda }{T}=lambda nu left(2.1right),]
где период – величина обратная частоте колебаний:
[T=frac{1}{nu }left(2.2right).]
Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).]
Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }]
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
[{left(frac{dxi }{dt}right)}_{max}=left|2omega right|left(2.4right).]
Циклическую частоту найдем как:
[omega =2pi nu ,]
тогда:
[{left(frac{dxi }{dt}right)}_{max}=left|2cdot 2pi nu right|=4pi nu .]
Вычислим максимальную скорость колебаний частиц:
[{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).]
Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$
Читать дальше: формула скорости свободного падения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Скорость распространения волны


4.6
Средняя оценка: 4.6
Всего получено оценок: 149.
4.6
Средняя оценка: 4.6
Всего получено оценок: 149.
Волны любой природы распространяются в пространстве не мгновенно, следовательно, это распространение имеет конечную скорость. Поговорим об этой скорости более подробно.
Распространение колебаний
Далеко не любые колебательные процессы приводят к распространению волн. Колебательная система представляет собой лишь источник колебаний. Для того, чтобы эти колебания могли распространяться, необходимо также существование упругой среды без разрывов, связанной с этим источником. Природа упругих сил может быть различна в различных средах, однако, их наличие обязательно, без этого второго условия, распространение волн в среде невозможно.

Каждая точка среды, через которую проходит волна, в простейшем случае начинает колебаться по гармоническому закону (в более сложных случаях колебания точек можно представить в виде суммы таких функций с различными параметрами):
$$x=Asin(omega t+varphi)$$
Однако, уравнение колебания соседних точек будет немного различаться. Во-первых, чем дальше точка расположена от источника колебаний, тем больше потерь происходит по пути, и тем меньше амплитуда колебаний (параметр $A$ в представленной формуле). Однако, когда потери невелики, заметное изменение амплитуды происходит лишь на больших расстояниях.
Гораздо важнее другое отличие – отличие фазы колебаний (параметр $varphi$ ) для различных точек. По мере удаления от источника колебаний, фаза плавно изменяется, постоянно увеличиваясь. Поскольку синус – круговая функция, то рано или поздно разность фаз между двумя точками становится равной ${2pi}$, а значит, эти две точки колеблются одинаково – синфазно. Для более далеких точек фаза увеличивается дальше, и для точек, разность фаз которых составит ${4pi}$ колебания опять будут синфазны.
Таким образом, по мере удаления от источника колебаний в среде будет ряд точек, колеблющихся в одной фазе. Минимальное расстояние между двумя такими точками называется длиной волны. Она обозначается греческой буквой $lambda$ (лямбда).
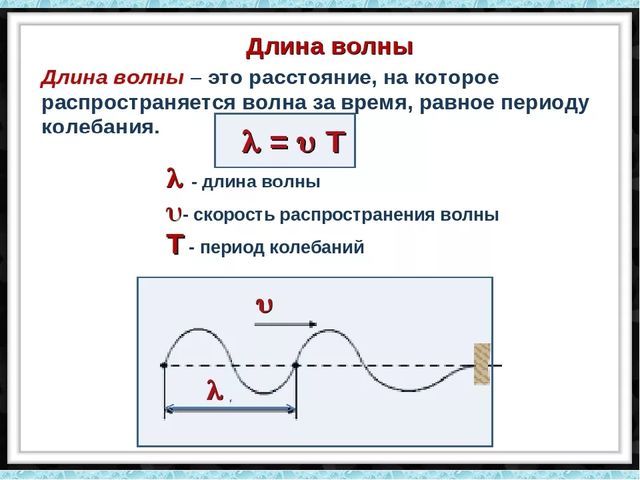
Скорость распространение волн
Плавное изменение фазы колебаний по мере удаления от источника колебаний можно представить в виде распространения этих колебаний, и определить скорость этого распространения. Разность фаз между ближайшими точками, колеблющимися синфазно, составляет $2pi$, это один период колебаний. А значит, волна проходит расстояние между этими точками за время одного периода $T$. Зная длину волны – можно вычислить скорость ее распространения:
$$v = {lambda over T}$$
Иногда известен не период, а частота колебаний $nu$. В этом случае формула скорости распространения волны примет вид:
$$v = {lambda nu}$$
Если среда первоначально была спокойна, то начало возмущений (иногда его называют «фронт волны») будет удаляться от источника колебаний как раз с указанной скоростью.


Что мы узнали?
Колебания среды распространяются не мгновенно, а с конечной скоростью. Каждая точка среды колеблется с некоторой фазой, которая изменяется, по мере удаления от источника колебаний. Минимальная длина между точками, колеблющимися синфазно, называется длиной волны, а отношение длины волны к периоду колебаний – скорости распространения волн.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 149.
А какая ваша оценка?
Рассмотрим
неустановившееся движение в открытом
прямоугольном русле (с горизонтальным
дном), считая, что потерями на трение
можно пренебречь. В этом случае
![]() и уравнения (19.14) записываются в виде
и уравнения (19.14) записываются в виде
![]() ,
,
(19.20)
где
![]() –
–
скорость перемещения отдельных точек
фронта волны.
Интегрируя (19.15) с
учетом того, что
![]() ,
,![]() получим
получим
![]() const.
const.
(19.21)
Найдя постоянную
интегрирования из начальных условий,
когда
![]() =const
=const
и
![]() =const,
=const,
получим
![]()
и
![]() ,
,
(19.22)
где
![]() –
–
первоначальная глубина наполнения;![]() ,
,![]() –
–
высота волны (рис. 19.7).
Средняя скорость
движения при неустановившемся движении
в прямоугольном горизонтальном русле
при отсутствии гидравлических
сопротивлений определяется по (19.22). С
использованием (19 22) из (19.20) получим
![]() .
.
(19.23)
Далее
![]() ;
;
(19.24)
![]() ;
;
(19.25)
![]() ,
,
(19.26)
где
![]() –
–
произвольная функция.
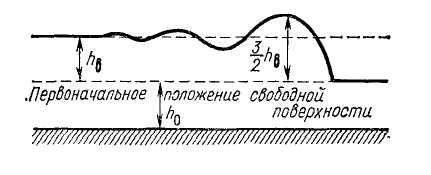
Рис. 19.7
В полученных
формулах знак плюс соответствует прямой
волне, знак минус – обратной. При этом
для положительной волны
![]() ,
,
для отрицательной![]() .
.
В соответствии с
(19.25) в волне, характеризующейся повышением
уровня (![]() ),
),
сечение с большей глубиной нагоняет
сечение с меньшей глубиной. Поэтому
мгновенные профили волны становятся
все более крутыми, при определенных
условиях волна может опрокинуться, т.е.
разрушиться. Для волн![]() сечение с меньшей глубиной отстает от
сечение с меньшей глубиной отстает от
сечения с большей глубиной и мгновенные
профили волны становятся все более
распластанными. Если изменение расхода,
вызвавшее появление положительной
волны, произошло достаточно быстро, то
фронт такой волны считают вертикальным,
хотя на самом деле положительная волна
в таких условиях начинается с переднего
вала высотой примерно![]() (рис. 19.7).
(рис. 19.7).
При медленном
изменении расхода (или отметки уровня,
или глубины), приведшем к появлению
положительной волны, ее фронт растянут.
От скорости
перемещения отдельных точек фронта
волны можно перейти к скорости
распространения фронта волны. Эту
скорость называют скоростью распространения
волны
![]() .
.
Ее находят из выражения
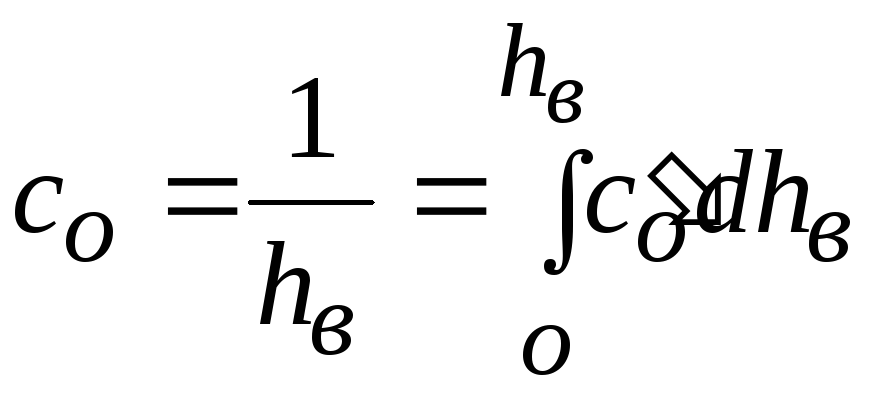 .
.
Подставив сюда
![]() по (19.25) и выполнив преобразования,
по (19.25) и выполнив преобразования,
получим
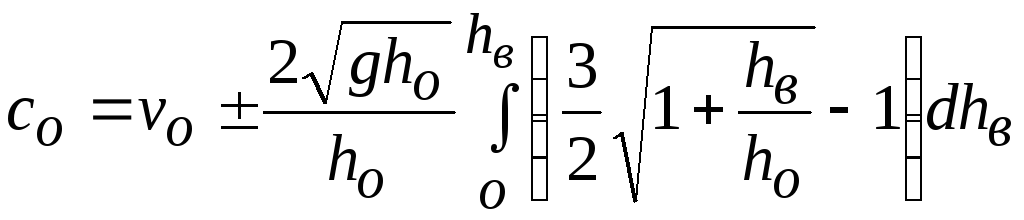 .
.
С учетом
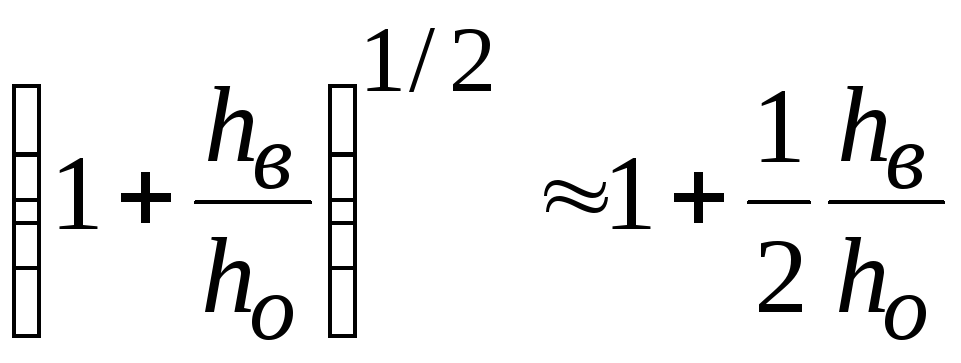
после интегрирования
получим
![]() .
.
(19.27)
Вновь для прямой
волны – знак плюс, для обратной волны –
знак минус.
При
![]() получим
получим
![]() .
.
(19.28)
Если волна
распространяется в неподвижной жидкости
(![]() ),
),
то получим формулу Лагранжа для этого
случая
![]() .
.
(19.29)
Все формулы даны
для случая, когда волна положительная,
т. е.
![]() .
.
При отрицательной
волне
![]() в формулах должна быть принята
в формулах должна быть принята
отрицательной.
Формулы, полученные
для прямоугольного русла, могут быть
применены для призматических русл с
другой формой поперечного сечения.
Следует при этом в формулах для
![]() и
и![]() заменить
заменить![]() на
на![]() ,
,
где![]() –
–
первоначальная площадь живого сечения;![]() –
–
ширина по верху живого сечения при![]() .
.
Формулы скорости
распространения волны (19.27) – (19.29) могут
быть применены и для реальных случаев,
когда силы сопротивления не равны нулю,
так как их влияние не сказывается
ощутимым образом на
![]() .
.
Соседние файлы в папке Штеренлихт
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Если бросить камень в воду водоема, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.

Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется.
Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.
Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.
Поскольку скорость волны – величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней: λυTТак как период Т и частота v связаны соотношением T = 1 / v, то скорость волны: υ = λ / Т = λ v
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.
Величины, характеризующие волну: длина волны, скорость волны, период колебаний, частота колебаний.

Единицы измерения в системе СИ:
длина волны [λ] = 1 м скорость распространения волны [ v ] = 1м/с период колебаний [ T ] = 1c
частота колебаний [ v ] = 1 Гц

Абсолютно все в этом мире происходит с какой-либо скоростью. Тела не перемещаются моментально, для этого требуется время. Не являются исключением и волны, в какой бы среде они не распространялись.
Если вы бросите камень в воду озера, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн.
Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется. Например, если вибрирующий железный лист засунуть концом в воду, то вода покроется рябью маленьких волн, однако скорость их распространения будет меньше, чем в железном листе.

Это несложно проверить даже в домашних условиях. Только не порежьтесь о вибрирующий железный лист. .
Длина волны
None Если зарисовать волну в виде рисунка или графика, то длиной волны будет являться расстояние между любыми ближайшими гребнями либо впадинами волны, либо между любыми другими ближайшими точками волны, находящимися в одинаковой фазе.
Так как длина волны это расстояние, пройденное ею, то и найти эту величину можно, как и любое другое расстояние, умножив скорость прохождения на единицу времени. Таким образом, длина волны связана со скоростью распространения волны прямо пропорционально. Найти длину волны можно по формуле:
λ=vT ,где λ длина волны, v скорость волны, T период колебаний.
А учитывая, что период колебаний обратно пропорционален частоте этих же колебаний: T=1⁄υ, можно вывести связь скорости распространения волны с частотой колебаний:
v=λυ .
[custom_ads_shortcode1]
Частота колебаний в разных средах
Частота колебаний волн не меняется при переходе из одной среды в другую. Так, например, частота вынужденных колебаний совпадает с частотой колебаний источника. Частота колебаний не зависит от свойств среды распространений. При переходе из одной среды в другую меняется лишь длина волны и скорость ее распространения.
Эти формулы справедливы как для поперечных, так и для продольных волн. При распространении продольных волн длина волны будет расстоянием между двумя ближайшими точками с одинаковым растяжением или сжатием. Она также будет совпадать с расстоянием, пройденным волной за один период колебаний, поэтому формулы будут полностью подходить и в этом случае.
[custom_ads_shortcode2]
Нужна помощь в учебе?
Предыдущая тема: Распространение колебаний в среде и волны: продольные и поперечные

Следующая тема: Источники звука и звуковые колебания: что это и как происходит
| Твитнуть | Нравится | Нравится |
Все неприличные комментарии будут удаляться.
Геометрическое место точек среды, для которых в некоторый момент времени фаза волны имеет одно и то же значение, называют волновой поверхностью или фронтом волны. ОпределениеСкорость перемещения фронта волны называется скоростью волны.

Если рассматривается одномерный случай гармонической волны, то уравнение волновой поверхности имеет вид:
[Ф_s=omega t-kx+varphi left(1right),] где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Условию (1) в каждый момент времени соответствует только одна точка оси X c координатой, равной:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).] Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне вырождается в точку. Из выражения (2) видно, что волновые поверхности с течением времени перемещаются в веществе со скоростью:
![]()
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right).] Для гармонических волн скорость движения поверхности волны совпадает со скоростью распространения волны. Скорость, определенная выражением (3) называют фазовой скоростью. В случае гармонической волны скорость распространения энергии совпадает с фазовой скоростью волны.
Скорость волны зависима от среды и типа волны. Скорость волны не надо путать со скоростью колебания частиц среды в волне.
[custom_ads_shortcode3]
Фазовая скорость распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях равна:
![]()
[v=sqrt{frac{K}{rho }}left(4right),] где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) справедлива, если избыточное давление много меньше, чем равновесное давление невозмущенного газа. Для определения скорости распространения продольных волн в газе используют формулу:
None Фазовая скорость распространения продольных волн в твердом теле:
[v=sqrt{frac{E}{rho }}left(6right),] где $E$ – модуль Юнга вещества стержня.
[custom_ads_shortcode1]
Фазовая скорость распространения поперечных волн
Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде можно вычислить как:
[v=sqrt{frac{G}{rho }left(7right),}] где $G$ – модуль сдвига среды; $rho $ – плотность вещества. Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
[custom_ads_shortcode2]
Групповая скорость волн
Для диспергирующих волн помимо фазовой скорости волны следует использовать такое понятие как групповая скорость. Если фазовая скорость зависит от частоты и в среде распространяются волны сложного негармонического характера, то при помощи групповой скорости характеризуют распространение волн.

Групповой скоростью называют скорость движения группы (цуга) волн, которые создают в каждый момент времени локализованный в пространстве волновой пакет. Любая реальная волна является суперпозицией гармонических волн. Скорость с которой такая волна распространяется в веществе, имеющем дисперсию на равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой: [u=v-frac{dv}{dlambda }left(8right).] Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тога фазовая и групповая скорости равны и не зависят от длины волны.
[custom_ads_shortcode3]
Примеры задач с решением
None Решение: Зная, что звук – продольная волна, за основу решения задачи примем формулу вычисления фазовой скорости продольной волны в газе:

[v=sqrt{frac{gamma p}{rho }}left(1.1right).] Будем считать азот идеальным газом. Тогда используем уравнение Менделеева – Клапейрона:
[pV=frac{m}{mu }RTleft(1.2right),] где $mu $ – молярная масса газа. Для азота она равна ${mu }_{N_2}=28cdot {10}^{-3}frac{кг}{моль}$; $R=8,31 frac{Дж}{мольcdot К}$ – универсальная газовая постоянная; $T$ – термодинамическая температура газа. Разделим обе части выражения (1.2) на объем:
None [frac{p}{rho }=frac{RT}{mu }left(1.4right),] подставим полученное отношение в (1.1) скорость звука найдем как:

None [gamma =frac{i+2}{i}=frac{7}{5},] так как молекула двух атомная имеет три степени свободы поступательного движения и две вращательного (рис.1).
Вычислим скорость звука в азоте:
[v=sqrt{frac{7}{5}cdot frac{8,31cdot 300}{28cdot {10}^{-3}}}approx 350 left(frac{м}{с}right).] Ответ: $v=350frac{м}{с}$Пример 2Задание: Какова скорость распространения волны в упругой среде, если разность фаз точек, которые находятся на расстоянии $Delta x,$ равна $Delta varphi $ при частоте колебаний равной $nu $?

Решение: Рассмотрим уравнение одномерной плоской волны:
None [{varphi }_1=omega t-kx_1+varphi ;; {varphi }_2=omega t-kx_2+varphi left(2.3right).] Найдем их разность:
None [omega =2pi nu left(2.5right).] Выражение (2.4) преобразуем к виду:
![]()
None [v=frac{2 pi nu Delta x}{Delta varphi }(frac{м}{с}).] Ответ: $v=frac{2 pi nu Delta x}{Delta varphi }frac{м}{с}$Читать дальше: скорость движения.
None Скоростью волны называют скорость, с которой движется фронт волны. Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),] где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:

[x=frac{omega t+varphi -Ф_s}{k}left(2right).] Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
None Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны. Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны – это не то же самое, что скорость колебания частиц среды в волне.
[custom_ads_shortcode1]
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как: [v=sqrt{frac{K}{rho }}left(4right),] где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение: [v=sqrt{frac{gamma p}{rho }}left(5right),] где $gamma $ – показатель адиабаты; $p$ – давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна: [v=sqrt{frac{E}{rho }}left(6right),] где $E$ – модуль Юнга вещества стержня.
[custom_ads_shortcode2]
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как: [v=sqrt{frac{G}{rho }left(7right),}] где $G$ – модуль сдвига среды; $rho $ – плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
[custom_ads_shortcode3]
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн. Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.

Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой: [u=v-frac{dv}{dlambda }left(8right).] Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
[custom_ads_shortcode1]
Примеры задач с решением
None Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
None [T=frac{t}{N} left(1.2right).] Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.] Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).] Ответ. $v=5frac{м}{с}$Пример 2Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды? Решение. Фазовую скорость движения волны найдем как:

None [T=frac{1}{nu }left(2.2right).] Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).] Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }] Максимальное значение скорости колебаний частиц в волне из (2.3) равно:

None [omega =2pi nu ,] тогда:
None [{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).] Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$Читать дальше: формула скорости свободного падения.
Источники:

- www.sites.google.com
- www.nado5.ru
- www.webmath.ru
- www.webmath.ru
