Содержание:
Равномерное движение:
В репортажах с автомобильных гонок, сообщениях о погоде можно, например, услышать: «Скорость движения автомобиля-победителя перед финишем достигла 250 километров в час»; «Скорость ветра достигала 25 метров в секунду» и т. п. Что это значит? Как сравнить эти скорости?
Слово «скорость» вы знаете давно. Поэтому, когда слышите, что скорость движения автомобиля составляет 20 метров в секунду, то понимаете: автомобиль, двигаясь с такой скоростью, каждую секунду проходит расстояние 20 м.
Подумайте, какое расстояние проедет этот автомобиль за 10 секунд; за полсекунды; за 0,1 секунды. Скорее всего, большинство из вас ответили так: за 10 с автомобиль проедет 200 м, за полсекунды — 10 м, за 0,1 с — 2 м. И эти ответы правильны, если считать, что за любые (малые или большие) равные интервалы времени автомобиль проезжает одинаковый путь. То есть если автомобиль движется равномерно.
Равномерное движение — это механическое движение, при котором тело за любые равные интервалы времени проходит одинаковый путь. Обратите внимание на слова «любые равные интервалы времени». Иногда, рассматривая даже неравномерное движение тела, можно выделить такие равные интервалы времени, за которые тело проходит одинаковые расстояния. Например, каждые 30 с пловец проплывает дорожку в бассейне (25 м), но нельзя утверждать, что он движется равномерно, ведь при развороте он замедляет движение.
Равномерное прямолинейное движение
Если автомобиль равномерно движется по прямолинейному участку дороги, то за равные интервалы времени он совершает одинаковые перемещения (рис. 8.1), то есть проходит одинаковый путь и не изменяет направления своего движения. Такое движение называют равномерным прямолинейным.
Равномерное прямолинейное движение — это механическое движение, при котором за любые равные интервалы времени тело совершает одинаковые перемещения. Равномерное прямолинейное движение — простейший вид движения, который в жизни встречается редко. Примерами такого движения могут быть движение автомобиля на прямолинейном участке дороги (без разгона и торможения), падение металлического шарика в растительном масле, полет парашютиста через некоторое время после раскрытия парашюта.
Определение скорости равномерного движения
Полагаем, вам несложно определить скорость равномерного движения, например, пешехода, который прошел 30 м за 20 с. Из курса математики вы хорошо знаете, что для этого нужно путь, который прошел пешеход (l = 30м), разделить на время его движения (t = 20c).
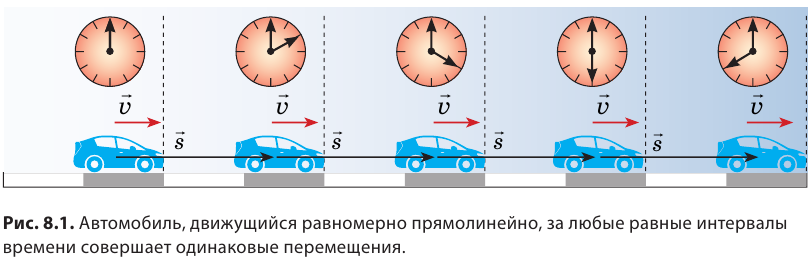
Скорость равномерного движения (v) — это физическая величина, равная отношению пути l, пройденного телом, к интервалу времени t, в течение которого этот путь был пройден: 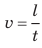
Обратите внимание! В ходе равномерного прямолинейного движения модуль перемещения равен пути ( s= )l, поэтому значение скорости движения можно определить по любой из формул: 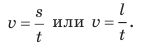 В Международной системе единиц путь измеряют в метрах, время — в секундах, поэтому единица скорости движения в СИ — метр в секунду:
В Международной системе единиц путь измеряют в метрах, время — в секундах, поэтому единица скорости движения в СИ — метр в секунду: 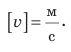
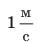 равен скорости такого равномерного движения, при котором тело за 1 с проходит путь 1 м. Прибором для прямого измерения скорости движения служит спидометр.
равен скорости такого равномерного движения, при котором тело за 1 с проходит путь 1 м. Прибором для прямого измерения скорости движения служит спидометр.
Скорость движения
Скорость движения — векторная величина: она имеет не только значение, но и направление. На рисунках направление скорости движения тела показывают стрелкой (см. рис. 8.1, 8.2).
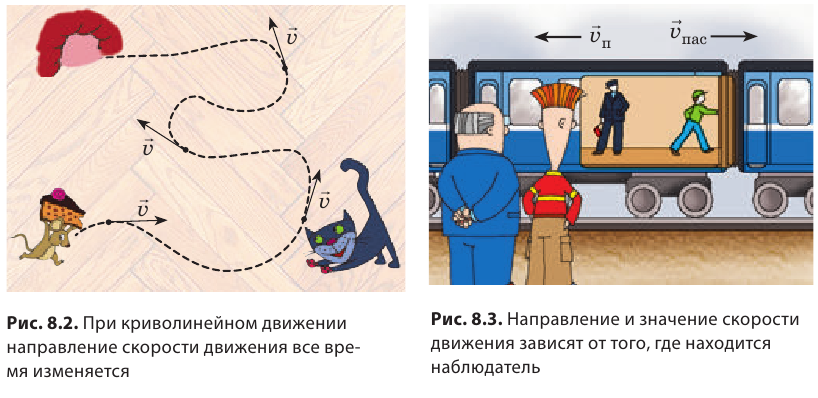
Если тело движется равномерно прямолинейно, то значение и направление скорости движения остаются неизменными (см. рис. 8.1). Если тело движется равномерно по криволинейной траектории, значение скорости движения остается неизменным, а направление все время изменяется (рис. 8.2). Направление и значение скорости движения зависят от того, относительно какого тела рассматривают движение. Представьте, что вы стоите в вагоне поезда, движущегося на восток (рис. 8.3). Поезд проезжает мимо станции со скоростью 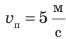 . В это время другой пассажир идет по вагону со скоростью
. В это время другой пассажир идет по вагону со скоростью 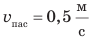 , двигаясь в направлении, противоположном движению поезда. Как вы считаете, одинаковой ли будет скорость движения пассажира для вас и для людей, стоящих на перроне? Конечно, нет! Для вас пассажир движется на запад со скоростью
, двигаясь в направлении, противоположном движению поезда. Как вы считаете, одинаковой ли будет скорость движения пассажира для вас и для людей, стоящих на перроне? Конечно, нет! Для вас пассажир движется на запад со скоростью 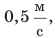 а для людей на перроне он вместе с поездом движется на восток со скоростью
а для людей на перроне он вместе с поездом движется на восток со скоростью 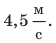
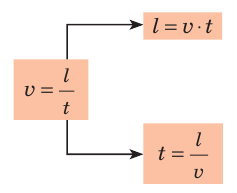
Значение скорости движения может быть выражено не только в метрах в секунду, но и в других единицах. Например, автомобиль движется со скоростью 36 километров в час 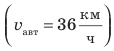 , ракета мчится со скоростью 8 километров в секунду
, ракета мчится со скоростью 8 километров в секунду  , улитка ползет со скоростью 18 сантиметров в минуту
, улитка ползет со скоростью 18 сантиметров в минуту 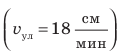 Для решения задач нужно научиться представлять скорость движения, данную в одних единицах, в других единицах. Например, скорость движения автомобиля — 36 км/ч. Чтобы представить эту скорость в метрах в секунду, вспомним, что 1 ч = 3600 с, а 1 км = 1000 м. Тогда:
Для решения задач нужно научиться представлять скорость движения, данную в одних единицах, в других единицах. Например, скорость движения автомобиля — 36 км/ч. Чтобы представить эту скорость в метрах в секунду, вспомним, что 1 ч = 3600 с, а 1 км = 1000 м. Тогда: 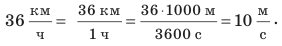 Попробуйте представить в метрах в секунду скорости движения ракеты и улитки (приведены выше). Сложнее переводить в другие единицы скорость движения, данную в метрах в секунду, но последовательность действий остается той же. Например, скорость движения самолета — 250 м/с. Представим ее в километрах в час, вспомнив, что 1 м = 0,001 км;
Попробуйте представить в метрах в секунду скорости движения ракеты и улитки (приведены выше). Сложнее переводить в другие единицы скорость движения, данную в метрах в секунду, но последовательность действий остается той же. Например, скорость движения самолета — 250 м/с. Представим ее в километрах в час, вспомнив, что 1 м = 0,001 км; 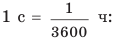
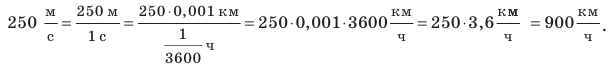
Чтобы скорость движения, представленную в метрах в секунду, выразить в километрах в час (и наоборот), можно воспользоваться схемой, приведенной на рис. 8.4.
Определяем путь и время движения тела
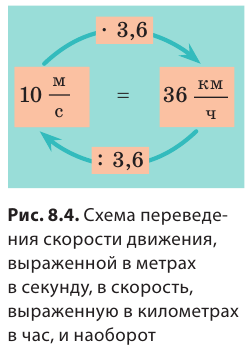
Из курса математики вы знаете: если известны скорость и время движения тела, то можно найти путь, который прошло тело. Для этого нужно скорость движения умножить на время: 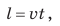 где l — путь; v — скорость движения; t — время движения с данной скоростью. Если известны путь и скорость движения тела, можно найти время движения тела. Для этого необходимо путь разделить на скорость движения:
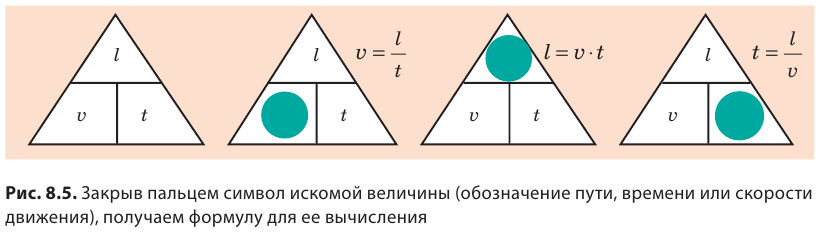
где l — путь; v — скорость движения; t — время движения с данной скоростью. Если известны путь и скорость движения тела, можно найти время движения тела. Для этого необходимо путь разделить на скорость движения: 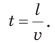 Иногда для определения пути, скорости или времени движения тела удобно пользоваться «волшебным треугольником» (рис. 8.5).
Иногда для определения пути, скорости или времени движения тела удобно пользоваться «волшебным треугольником» (рис. 8.5).
Итоги:
Равномерное движение — это механическое движение, при котором за любые равные интервалы времени тело проходит одинаковый путь. Равномерное прямолинейное движение — это механическое движение, при котором за любые равные интервалы времени тело совершает одинаковые перемещения. Скорость равномерного движения — это физическая величина, равная отношению пути, который прошло тело, к интервалу времени, в течение которого этот путь был пройден: 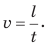 Единица скорости движения в СИ — метр в секунду (м/с). Спидометр — прибор для прямого измерения скорости движения тела. Кроме значения скорость движения имеет направление. Направление и значение скорости движения тела зависят от выбора системы отсчета.
Единица скорости движения в СИ — метр в секунду (м/с). Спидометр — прибор для прямого измерения скорости движения тела. Кроме значения скорость движения имеет направление. Направление и значение скорости движения тела зависят от выбора системы отсчета.
Может, вы будете удивлены, но в повседневной жизни вы уже встречались с физическими задачами и даже решали их. Приведем несколько примеров физических задач, прокомментируем основные этапы их решения, и в дальнейшем вы будете подходить к решению таких задач как настоящие физики.
Пример №1
Предположим, что до начала уроков остается 15 минут, а вы знаете, что расстояние от вашего дома до школы равно 1800 м. Придете ли вы вовремя, если будете идти со скоростью 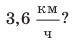
С какой наименьшей скоростью вы должны идти, чтобы не опоздать? Анализ физической проблемы. В задаче нужно найти: 1) время 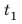 движения до школы с указанной скоростью
движения до школы с указанной скоростью 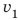 ; 2) наименьшую скорость
; 2) наименьшую скорость 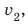 с которой следует идти, чтобы затратить на путь не более 15 мин
с которой следует идти, чтобы затратить на путь не более 15 мин 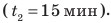 Движение будем считать равномерным. Скорость движения дана в
Движение будем считать равномерным. Скорость движения дана в  , а путь — в единицах СИ. Представим время и значение скорости движения в единицах СИ:
, а путь — в единицах СИ. Представим время и значение скорости движения в единицах СИ: 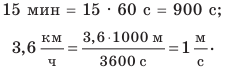 Закончив анализ, запишем краткое условие задачи.
Закончив анализ, запишем краткое условие задачи.
Дано:
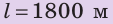 ,
, 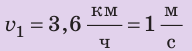 ,
,  .
.
Найти:
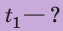 ,
, .
.
Решение:
Движение равномерное, поэтому воспользуемся формулой для расчета скорости равномерного движения: 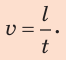
Найдем выражения для расчета искомых величин 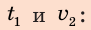
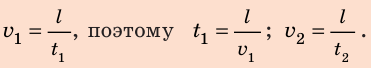
Проверим единицы искомых величин:
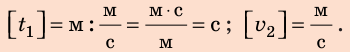
Найдем числовые значения искомых величин:
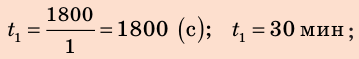
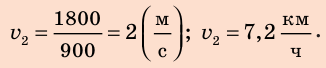
Обратите внимание! Для получения ответа в выражение для искомой величины можно сразу подставлять и числовые значения, и единицы известных величин. В этом случае запись будет такой:
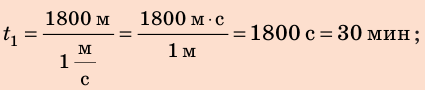
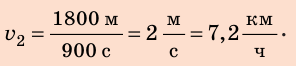
Анализ результатов. Поскольку 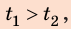 то, двигаясь со скоростью
то, двигаясь со скоростью 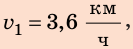 вы не успеете к началу уроков. Чтобы не опоздать, нужно двигаться со скоростью, значение которой больше
вы не успеете к началу уроков. Чтобы не опоздать, нужно двигаться со скоростью, значение которой больше 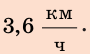 Именно такое значение получено в ходе решения. Следовательно, полученные значения искомых величин вполне правдоподобны.
Именно такое значение получено в ходе решения. Следовательно, полученные значения искомых величин вполне правдоподобны.
Ответ: 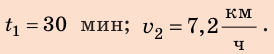



Пример №2
По озеру навстречу друг другу равномерно прямолинейно движутся два катера. На начало наблюдения расстояние между катерами составляло 1500 м. Скорость движения первого катера равна 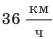 , второго —
, второго — 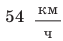 . Через какое время катера встретятся? Какое расстояние пройдет до встречи первый катер? Анализ физической проблемы. Катера движутся навстречу друг другу. Это значит, что они приближаются друг к другу со скоростью
. Через какое время катера встретятся? Какое расстояние пройдет до встречи первый катер? Анализ физической проблемы. Катера движутся навстречу друг другу. Это значит, что они приближаются друг к другу со скоростью 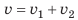 с этой же скоростью проходят расстояние l =1500 м. Задачу будем решать в единицах СИ.
с этой же скоростью проходят расстояние l =1500 м. Задачу будем решать в единицах СИ.
Дано:
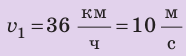 ,
,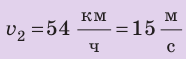 ,
,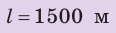 .
.
Найти:
 ,
, .
.
Решение:
По определению скорости движения:
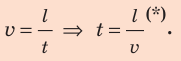
Так как 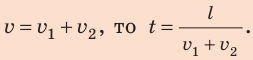
Зная время t и скорость движения 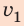 , определим путь
, определим путь 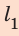 , который пройдет первый катер до встречи:
, который пройдет первый катер до встречи:
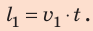
Проверим единицы искомых величин:
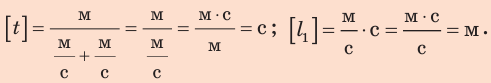
Определим числовые значения искомых величин:
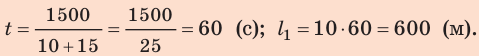
Анализ результатов. Так как первый катер движется медленнее второго, то до момента встречи он пройдет меньший путь. Такой результат и получен: 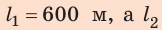 соответственно
соответственно 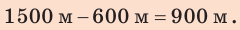 Поэтому результаты вполне реальны.
Поэтому результаты вполне реальны.
Ответ: 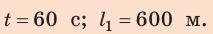
Графики равномерного движения
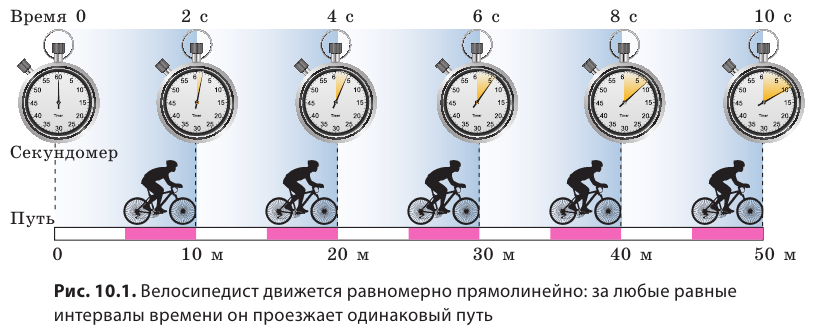
Велосипедист едет по трассе (рис. 10.1). Скорость движения, которую показывает спидометр велосипеда в любой момент времени, равна 5 м/с. Как описать движение велосипедиста и вообще любого тела с помощью графиков? Вспомним, ведь графики движения тел вы изучали в курсе математики 6 класса.
- Заказать решение задач по физике
График зависимости пути от времени для равномерного движения тела
Построим график зависимости пути, который проезжает велосипедист (см. рис. 10.1), от времени наблюдения — график пути. Для построения графика выполним следующие действия.
1. Заполним таблицу соответствующих значений времени t движения спортсмена и пути l, который он преодолевает за это время. Понятно, что в момент начала наблюдения t(=0 )путь равен нулю l(=0 . )За время t=2 c велосипедист преодолеет расстояние 10 м: 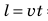
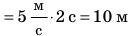
Рассуждая аналогично, получим:

2. Проведем две взаимно перпендикулярных оси. На горизонтальной оси — оси абсцисс — отложим время движения велосипедиста в секундах (t, с) так, что одной клетке будет соответствовать интервал времени 2 с. На вертикальной оси — оси ординат — отложим путь в метрах (l, м) так, что одной клетке будет соответствовать путь, равный 10 м (рис. 10.2, а).
3. Построим точки с координатами: (0; 0), (2; 10), (4; 20), (6; 30), (8; 40), (10; 50). Абсциссы данных точек соответствуют времени движения спортсмена, ординаты соответствуют пути, который он проехал за это время (рис. 10.2, б).
4. Соединим построенные точки линией (рис. 10.2, в). Полученный отрезок прямой — график пути велосипедиста.
Обратите внимание! Велосипедист движется равномерно, поэтому путь, который он проезжает, можно определить по формуле 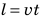 , в любой момент времени
, в любой момент времени 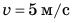 ; поэтому можно записать:
; поэтому можно записать: 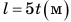 , где время t дано в секундах. Равенство
, где время t дано в секундах. Равенство 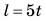 — уравнение зависимости пути, который проезжает велосипедист, от времени наблюдения.
— уравнение зависимости пути, который проезжает велосипедист, от времени наблюдения.
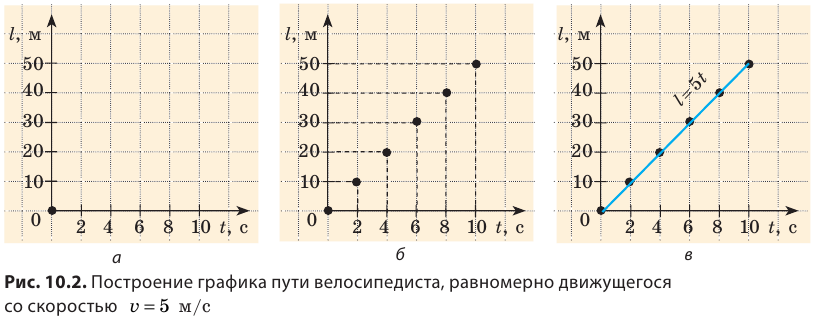
При равномерном движении график пути — это всегда отрезок прямой, наклоненной под определенным углом к оси времени. Поэтому для построения графика пути достаточно определить путь l для двух значений времени t и через полученные две точки провести отрезок прямой. Например, чтобы построить график пути велосипедиста, можно взять время начала наблюдения t(=0 )и время окончания наблюдения ( t = 10 с) (рис. 10.3).
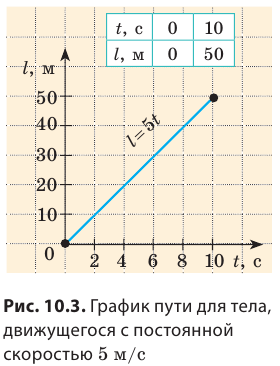
Что можно узнать по графику пути
График пути дает много полезной информации.
По графику пути можно:
- выяснить характер движения тела;
- определить путь, который проходит тело за определенный интервал времени;
- определить скорость движения тела;
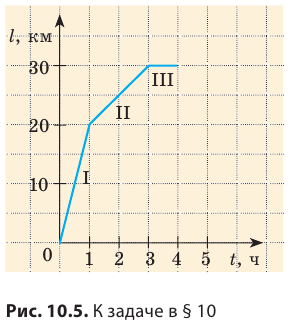
- сравнить скорости движения тел: чем больше скорость движения тела, тем больше угол между графиком пути и осью времени (рис. 10.4).
Рассмотрим пример:
Пример №3
По графику пути, представленному на рис. 10.5, узнайте: 1) как двигалось тело; 2)какой путь прошло тело за первый час; за следующие два часа; 3) какой была скорость движения тела на каждом участке.
Решение:
По графику видим, что весь путь состоит из трех участков, на каждом из которых тело двигалось равномерно (график пути тела — отрезки прямых). Участок I. По графику видим, что путь, пройденный телом за первый час, равен 20 км, поэтому скорость движения тела составляла:  Участок ІI. За следующие два часа тело прошло путь
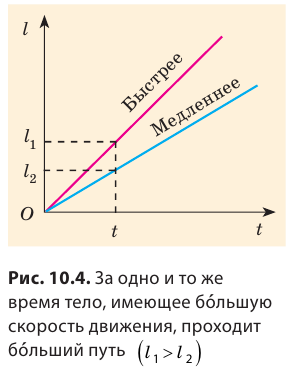
Участок ІI. За следующие два часа тело прошло путь 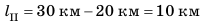 . Соответственно скорость движения тела была равна:
. Соответственно скорость движения тела была равна: 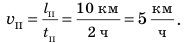
Участок ІІI. Последний час путь не изменялся, значит, тело остановилось: 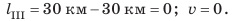 Анализ результатов. По графику видим, что участок I графика образует с осью времени больший угол, чем участок IІ. Поэтому участок І соответствует большей скорости движения тела.
Анализ результатов. По графику видим, что участок I графика образует с осью времени больший угол, чем участок IІ. Поэтому участок І соответствует большей скорости движения тела.
Строим график скорости равномерного движения тела
Вернемся к велосипедисту, движущемуся равномерно со скоростью v = 5 м/с (см. рис. 10.1). Построим график зависимости скорости его движения от времени наблюдения — график скорости движения. Для построения графика выполним следующие действия.
1. Заполним таблицу соответствующих моментов времени t движения велосипедиста и скорости движения v, которую он имел в эти моменты времени:

Велосипедист двигался равномерно, поэтому скорость его движения оставалась неизменной в течение всего времени наблюдения.
2. Проведем две взаимно перпендикулярных оси. На оси абсцисс отложим время движения велосипедиста в секундах (t, с), на оси ординат — скорость движения в метрах в секунду 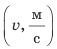 (рис. 10.6).
(рис. 10.6).
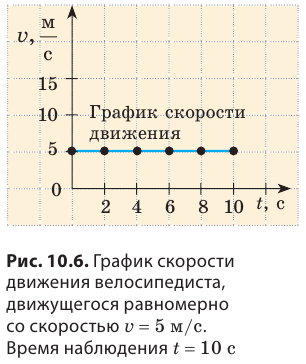
3. Построим точки с координатами (0; 5), (2; 5), (4; 5), (6; 5), (8; 5), (10; 5). Абсциссы указанных точек соответствуют времени движения спортсмена, ординаты — скорости его движения.
4. Соединим точки линией. Полученный отрезок прямой — график скорости движения велосипедиста. При равномерном движении график скорости движения тела — отрезок прямой, параллельной оси времени.
Что можно узнать по графику скорости движения тела
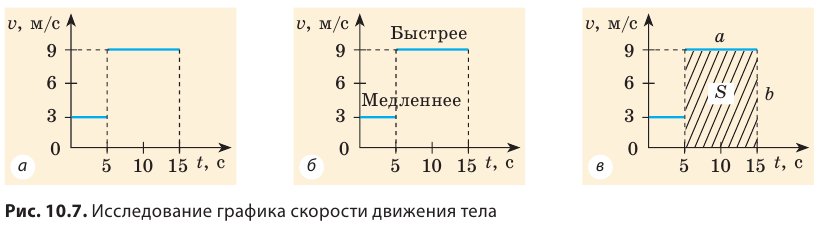
Рассмотрим график скорости движения некоторого тела (рис. 10.7, а) и узнаем о движении данного тела как можно больше.
1. В течение интервалов времени от 0 до 5 с и от 5 до 15 с тело двигалось равномерно, поскольку соответствующие участки графика скорости его движения — отрезки прямых, параллельных оси времени.
2. Скорость движения тела в течение последних 10 с наблюдения больше, чем в течение первых 5 с, поскольку второй участок графика расположен дальше от оси времени, чем первый участок (рис. 10.7, б).
В данном случае: 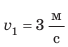 — на интервале времени от 0 до 5 с;
— на интервале времени от 0 до 5 с; 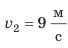 — на интервале времени от 5 до 15 с. 3. Можно определить путь l, который прошло тело (вспомните:
— на интервале времени от 5 до 15 с. 3. Можно определить путь l, который прошло тело (вспомните: 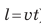 ). Так, за интервал времени от 5 до 15 с тело прошло путь 90 м:
). Так, за интервал времени от 5 до 15 с тело прошло путь 90 м: 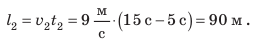 Этот путь численно равен площади заштрихованного прямоугольника (рис. 10.7, в):
Этот путь численно равен площади заштрихованного прямоугольника (рис. 10.7, в): 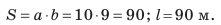 Обратите внимание! Для любого движения числовое значение пути, который прошло тело, равно числовому значению площади фигуры под графиком скорости движения этого тела.
Обратите внимание! Для любого движения числовое значение пути, который прошло тело, равно числовому значению площади фигуры под графиком скорости движения этого тела.
Итоги:
При равномерном движении тела график пути — это всегда отрезок прямой, наклоненной под определенным углом к оси времени, а график скорости движения — это отрезок прямой, параллельной оси времени.
По графику пути можно:
- узнать, как двигалось тело;
- вычислить путь, который прошло тело за определенный интервал времени;
- вычислить и сравнить скорости движения тел: чем больше скорость движения тела, тем больше угол между графиком пути и осью времени.
По графику скорости движения можно:
- узнать, как двигалось тело;
- вычислить путь, который прошло тело за определенный интервал времени;
- вычислить и сравнить скорости движения тел: чем больше скорость движения тела, тем дальше от оси времени расположен график скорости его движения.
- Неравномерное движение
- Вращательное движение тела
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Движение и взаимодействие
- Относительность движения
- Поступательное движение
- Равномерное и неравномерное движение
Определите скорость равномерного движения шарика !
Для этого измерьте любой участок путе , пройденный шариком за 1с , 2c , 3 c !
Рассчитайте скорость равномерного движения шарик по формуле v = s : t.
На этой странице вы найдете ответ на вопрос Определите скорость равномерного движения шарика ?. Вопрос
соответствует категории Физика и уровню подготовки учащихся 5 – 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
Скорость равномерного движения тела


4.2
Средняя оценка: 4.2
Всего получено оценок: 285.
4.2
Средняя оценка: 4.2
Всего получено оценок: 285.
Важнейшим параметром движения в кинематике является скорость. Рассмотрим особенности этой характеристики для случая равномерного движения тела.
Равномерное движение тела
Если тело движется, то путь, пройденный им постоянно увеличивается. Однако, если мы будем отмечать путь, пройденный движущимся телом за каждую секунду или каждый час (или любой другой одинаковый промежуток времени), то этот путь не обязательно будет увеличиваться. Он может и уменьшаться, и оставаться без изменения, и даже может быть нулевым (ясно, что в этом случае тело покоится на месте).
Движение, при котором за равные промежутки времени тело проходит равный путь, называется равномерным.

Хотя, в природе равномерные движения достаточно редки, в жизни человека таких движений гораздо больше. Эталон равномерного движения – стрелки часов, которые каждый час проходят один и тот же путь по циферблату.
Скорость, как главная характеристика движения
На примере стрелок часов – часовой, минутной и секундной – можно видеть разницу в движении. Хотя все эти три стрелки проходят за равные промежутки времени равные пути, а значит, все три движутся равномерно, двигаются они совершенно по-разному.
Для характеристики этой разницы введено понятие скорости.
Скорость равномерного движения тела равна пути, проходимому телом за единицу времени.
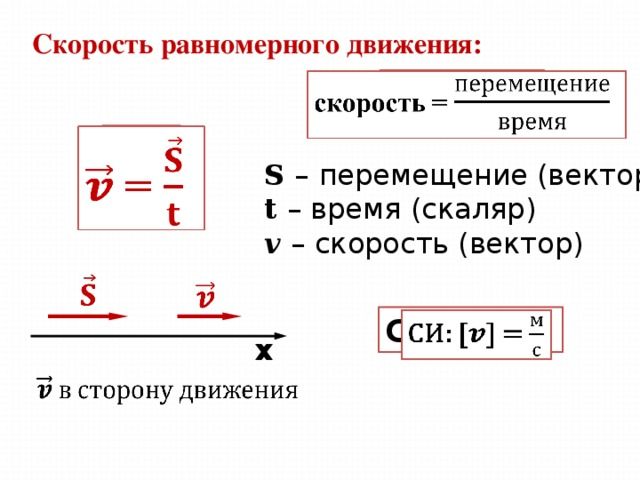
То есть, для нахождения скорости надо найти отношение пройденного пути ко времени, за который этот путь был пройден. Поскольку при равномерном движении тело за любой равный промежуток времени проходит одно и то же время, то это отношение будет всегда одинаковым. Формула скорости равномерного движения:
$$v={s over t},$$
где:
- $v$ – скорость;
- $s$ – путь;
- $t$ – время;
Таким образом, физический смысл скорости – это путь, проходимый телом в единицу времени.
Из этой же формулы можно найти размерность скорости. Поскольку расстояние в системе СИ измеряется в метрах, а время в секундах, то единицей скорости является:
$$v={s over t}={м over сек}$$
то есть, метры в секунду.
Хотя математически скорость может принимать любое значение, в реальном мире скорость любого материального тела не может быть больше скорости света в вакууме. Она равна примерно $3×10^8$ м/с.
Скорость – векторная величина
Полученное значение говорит о величине скорости. Однако, эта характеристика не единственная.
Представим себе, что нам надо через 10 часов прибыть на северный полюс, до которого 10 тысяч километров, на самолете, движущемся со скоростью тысяча километров в час. Если самолет летит точно на север, он прибудет вовремя. А что будет, если самолет полетит на восток ? Мы не достигнем цели не только через 10 часов, но и вообще никогда.
Из этого примера можно видеть важнейшую особенность скорости – она имеет направление. Величины, не имеющие направления, называются скалярными. Величины, имеющие направление, называются векторными.

Скорость – одна из векторных величин. Для полного определения скорости необходимо указывать не только ее величину, но и направление.

Что мы узнали?
Скорость равномерного движения равна отношению пройденного пути ко времени, за который этот путь был пройден. Скорость измеряется в метрах в секунду и является векторной величиной.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 285.
А какая ваша оценка?
Содержание:
- Прямолинейное равнопеременное движение
- Средняя скорость неравномерного движения
- Мгновенная скорость
- Ускорение
- Единица ускорения
- Равноускоренное движение
- Скорость равноускоренного движения
- График скорости равноускоренного движения
- Графический способ вывода формулы пути равноускоренного движения
- Средняя скорость равноускоренного движения
- Уравнения равноускоренного движения
- Пути, проходимые в равноускоренном движении за равные последовательные промежутки времени
- Свободное падение тел
- Равнозамедленное движение
- Движение тела, брошенного вертикально вверх
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково. Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Прямолинейное равнопеременное движение
Равнопеременное прямолинейное движение. Равнопеременным прямолинейным движением называется дви–жение, при котором за любые равные промежутки времени скорость те-ла изменяется на одинаковую величину и траектория – прямая линия.
Средняя скорость неравномерного движения
Большинство движений, наблюдаемых нами в природе и технике,— движения переменные, то есть неравномерные. Таковы, например, движения автомобиля, трактора, поезда, людей, животных и др.
Для характеристики неравномерного движения на каком-нибудь участке пути вводится понятие средней скорости движения.
Рассмотрим пример. Допустим, что расстояние от Москвы до Горького (440 км) поезд прошёл за 11 час. Движение поезда на всём пути было явно неравномерное: он то ускорял движение, то замедлял и даже останавливался на промежуточных станциях. Но если бы путь в 440 км поезд прошёл за 11 час., двигаясь равномерно, то его скорость была бы:  Скорость 40
Скорость 40  является средней скоростью неравномерного движения на участке Москва — Горький.
является средней скоростью неравномерного движения на участке Москва — Горький.
Средняя скорость неравномерного движения на данном участке пути измеряется отношением длины участка пути к промежутку времени, в течение которого этот путь пройден

Но так же рассчитывается и скорость равномерного движения. Следовательно, можно сказать, что средняя скорость неравномерного движения равна скорости такого равномерного движения, при котором тело проходит тот же путь и за такой же промежуток времени, как и при данном неравномерном движении.
Если известны время и средняя скорость неравномерного движения на некотором участке пути, то длину этого участка пути можно рассчитать по формуле:

Мгновенная скорость
В каждый момент времени тело движется с определённой скоростью, и каждому моменту времени соответствует определённая точка на траектории.

Рис. 32. К понятию мгновенной скорости.
Скорость, которую имеет тело в данный момент времени или в данной точке траектории, называется мгновенной скоростью.
При равномерном движении тела его скорость во всех точках траектории одинакова. Это и будет его мгновенная скорость. Сложнее дело обстоит е случае неравномерного движения.
Допустим, что тело, двигаясь неравномерно-прямолинейно, за t сек. прошло путь АВ — s (рис. 32). Средняя скорость этого движения  Эта скорость, вообще говоря, не характеризует движения в какой-нибудь точке пути С и не-определяет величину скорости в этой точке. Чтобы определить скорость в точке С, поступим следующим образом.
Эта скорость, вообще говоря, не характеризует движения в какой-нибудь точке пути С и не-определяет величину скорости в этой точке. Чтобы определить скорость в точке С, поступим следующим образом.
Разобьём весь наш путь АВ на отдельные участки и определим среднюю скорость на участке пути  меньшем АВ; затем на участке
меньшем АВ; затем на участке  меньшем
меньшем  и т. д., всё ближе и ближе подходя к точке С. По мере уменьшения участка пути, включающего точку С, а следовательно, и по мере уменьшения промежутка времени, за который этот участок проходится, изменение скорости на нём будет всё меньше и меньше. Движение за такие малые промежутки времени практически будет равномерным; скорость этого движения и можно принять за мгновенную скорость неравномерного движения в заданной точке траектории.
и т. д., всё ближе и ближе подходя к точке С. По мере уменьшения участка пути, включающего точку С, а следовательно, и по мере уменьшения промежутка времени, за который этот участок проходится, изменение скорости на нём будет всё меньше и меньше. Движение за такие малые промежутки времени практически будет равномерным; скорость этого движения и можно принять за мгновенную скорость неравномерного движения в заданной точке траектории.
Подобные рассуждения можно провести относительно любой точки, взятой на траектории АВ.
Подкрепим теперь наши общие.рассуждения о мгновенной скорости числовыми данными. Допустим, что четыре наблюдателя определяют скорость автомобиля в момент его прохождения мимо какого-нибудь предмета у дороги. С момента прохождения автомобиля мимо этого предмета все наблюдатели одновременно измеряют пути, пройденные автомобилем от этого предмета за различные промежутки времени. Результаты их наблюдений следующие:
Какая же из полученных величин скорости ближе к мгновенной скорости, которую имел автомобиль, проезжая мимо указанного выше предмета?

Рис. 33. Определение мгновенной скорости на опыте.
Такой скоростью, очевидно, будет скорость, вычисленная из результата измерений четвёртого наблюдателя, так как за 3 сек. автомобиль меньше всего изменил свою скорость. Итак, чем меньше взять промежуток времени, тем точнее можно определить искомую скорость тела в заданный момент времени.
Мгновенную скорость можно определить на опыте. Обратимся к рисунку 33. С наклонной плоскости скатывается тележка с капельницей. По отметкам, оставляемым капельницей, легко установить, что тележка движется неравномерно. Допустим, нам нужно определить мгновенную скорость тележки в какой-либо точке наклонной плоскости, например у её основания С. Для этого к наклонной плоскости в точке С присоединим горизонтальный жёлоб СВ,
Пользуясь капельницей; так же как в опыте, описанном на странице 13, легко установить, что когда тележка проходит точку С, то дальше она на небольшом отрезке пути отточки С движется равномерно. Следовательно, скорость в точке Сбудет такой же, как на всём дальнейшем пути равномерного движения. Отмечая время равномерного движения какой-либо точки на тележке и измеряя пройденный ею путь, можно определить скорость равномерного движения; она и будет искомой мгновенной скоростью в точке С.
Для определения мгновенной скорости в какой-либо другой точке А нужно только поднять горизонтальную часть плоскости СВ на уровень точки А и произвести такие же измерения, как и для точки С.
Мгновенные скорости движения автомобиля отмечаются стрелкой на шкале спидометра.
Ускорение
Среди разнообразных переменных движений встречаются движения, в которых скорость непрерывно возрастает. Такие движения называются ускоренными.
Ускоренно, например, движется поезд, отходящий от станции и постепенно увеличивающий свою скорость, поднимающийся в воздух самолёт, пуля в канале ружья и т. д. В сущности начало всякого движения является движением ускоренным, так как всякое тело, начиная двигаться, не мгновенно „набирает“ свою скорость.
В разных ускоренных движениях скорость изменяется по-разному—в одних быстрее, в других медленнее. Сравним, например, движение поезда при отходе со станции с движением снаряда в стволе орудия при выстреле. Оба эти движения ускоренные. Но в то время как скорость поезда возрастает медленно, скорость снаряда за какие-нибудь сотые доли секунды увеличивается от нуля до сотен метров в секунду.
Таким образом, ускоренные движения отличаются одно от другого быстротой изменёния скорости.
Характеристикой быстроты изменения скорости является особая величина, называемая ускорением. Чем быстрее изменяется скорость движения, тем больше величина ускорения.
Обозначим начальную скорость переменного движения тела  а скорость его через t сек.
а скорость его через t сек.  тогда изменение скорости за этот промежуток времени равно
тогда изменение скорости за этот промежуток времени равно  Допустим, что скорость движения изменяется равномерно; тогда изменение скорости за одну секунду будет равно:
Допустим, что скорость движения изменяется равномерно; тогда изменение скорости за одну секунду будет равно: 
Величина, измеряемая отношением изменения скорости к тому промежутку времени, за которое это изменение произошло, называется ускорением.
Обозначив ускорение буквой а, мы можем написать:

Пусть, например, в некоторый момент времени скорость пули в стволе винтовки была 100  , а через 0,0014 сек. стала 800
, а через 0,0014 сек. стала 800  . Значит, за 0,0014 сек. скорость пули изменилась на
. Значит, за 0,0014 сек. скорость пули изменилась на
800  —100
—100  = 700
= 700  .
.
Ускорение движения пули внутри ствола винтовки будет равно:
 или
или  за секунду.
за секунду.
Мы узнали, что ускорение движения пули внутри ствола  за секунду. Как это надо представлять себе? Это надо представлять так, что при равномерном нарастании скорость пули за 1 сек. увеличилась бы на
за секунду. Как это надо представлять себе? Это надо представлять так, что при равномерном нарастании скорость пули за 1 сек. увеличилась бы на  . Конечно, это не значит, что пуля внутри ствола на самом деле будет двигаться 1 сек.
. Конечно, это не значит, что пуля внутри ствола на самом деле будет двигаться 1 сек.
Единица ускорения
Установим теперь единицу ускорения. Положив  ед. скорости и t=1 ед. времени в формуле
ед. скорости и t=1 ед. времени в формуле  получим а = 1 ед. ускорения.
получим а = 1 ед. ускорения.
Это значит, что единицей ускорения является ускорение такого движения, при котором за единицу времени скорость изменяется на единицу скорости.
Если измерять скорость в  а время в секундах, то единицей ускорения будет ускорение такого движения, в котором за 1 сек. скорость изменяется на
а время в секундах, то единицей ускорения будет ускорение такого движения, в котором за 1 сек. скорость изменяется на  Наименование такой единицы ускорения:
Наименование такой единицы ускорения: 
Приняв за единицу скорости  а за единицу времени 1 сек., мы получим единицу ускорения
а за единицу времени 1 сек., мы получим единицу ускорения 

Этими двумя единицами чаще всего и измеряют ускорение, но, вообще говоря, за единицу ускорения можно принимать  и т.д.
и т.д.
Численное значение ускорения, как и любой другой физической величины, зависит от выбора единиц измерения.
П р и м е р. Ускорение некоторого движения равно  Выразить это ускорение в
Выразить это ускорение в


Равноускоренное движение
Познакомимся с ускоренным движением на опыте.

Рис. 34. Положения шарика через равные промежутки времени при его движении по наклонному жёлобу (отмечены флажками).
Установим наклонно жёлоб и предоставим шарику скатываться по нему. Определим пройденные шариком пути за одну, две, три и т. д. секунды. На рисунке 34 положения шарика на жёлобе в конце каждой из этих секунд обозначены флажками и помечены буквами 
 Расстояние
Расстояние  есть путь, пройденный шариком в течение первой секунды,
есть путь, пройденный шариком в течение первой секунды,  —путь, пройденный шариком в течение второй секунды,
—путь, пройденный шариком в течение второй секунды,  —в течение третьей секунды и
—в течение третьей секунды и  — в течение четвёртой секунды. Эти расстояния личиваются, следовательно, скорость шарика его движения по наклонному жёлобу возрастала.
— в течение четвёртой секунды. Эти расстояния личиваются, следовательно, скорость шарика его движения по наклонному жёлобу возрастала.
Чтобы установить закон возрастания скорости, измерим мгновенные скорости, которые будет иметь центр шарика в конце первой,второй, третьей и т. д. секунды.

Рис. 35. К установлению закона изменения скорости при движении шарика по наклонному жёлобу.
Для этого от нижнего конца наклонного жёлоба вверх по нему (рис. 35) отложим расстояния  и
и  проходимые шариком за одну, две, три секунды, и будем скатывать шарик сначала от
проходимые шариком за одну, две, три секунды, и будем скатывать шарик сначала от  затем от
затем от  и, наконец, от
и, наконец, от 
Скатившись с наклонного жёлоба, шарик будет двигаться с разными скоростями, причём во всех случаях на некотором отрезке горизонтального пути движение шарика будет равномерным.
Измерив в каждом случае путь, пройденный шариком по горизонтальной плоскости за 1 сек., мы найдём скорость шарика на участке равномерного движения, т. е. его мгновенную скорость в точке о.
В одном из опытов были получены следующие численные значения мгновенных скоростей шарика:

В этом опыте скорость движения шарика по наклонному жёлобу увеличивалась за 1 сек. на одну и ту же величину (на 20  ), т. е. шарик двигался с ускорением 20
), т. е. шарик двигался с ускорением 20 
Движение, при котором в любые равные промежутки времени скорость увеличивается на одну и ту же величину, называется равноускоренным.
Движение шарика по наклонному жёлобу есть равноускоренное движение.
Равноускоренное движение является одним из простейших видов ускоренных движений. Для равноускоренного движения, как мы увидим, зависимость скорости и пути от времени можно выразить простыми математическими формулами.
Скорость равноускоренного движения
В равноускоренном движении ускорение на всём протяжении пути не меняется, поэтому равноускоренное движение есть движение с постоянным ускорением.
Скорость в равноускоренном движении каждую секунду увеличивается на одну и ту же величину, численно равную ускорению.
Рассмотрим, как можно рассчитать скорость равноускоренного движения в конце какого-нибудь промежутка времени, если известны начальная скорость и ускорение.
Пусть в начале наблюдения скорость тела, например поезда, равна  и поезд движется с ускорением
и поезд движется с ускорением 
Чему будет равна скорость поезда через t секунд?
Нам уже известно, что ускорение равноускоренного движения показывает, на сколько возрастает скорость за каждую секунду.
В нашем примере ускорение равно  Значит, скорость поезда ежесекундно возрастает на
Значит, скорость поезда ежесекундно возрастает на  в течение t секунд скорость возрастёт на величину, в t раз большую, т. е. на
в течение t секунд скорость возрастёт на величину, в t раз большую, т. е. на 
Так как в начале наблюдения скорость поезда была равна  и через t сек она возросла на
и через t сек она возросла на  то в конце промежутка времени t она будет равна
то в конце промежутка времени t она будет равна 
Если обозначить скорость тела в конце промежутка времени t через  то можно написать:
то можно написать:

Что изменится, если начальная скорость будет равной, например,  и ускорение
и ускорение  или соответственно
или соответственно  и
и 
Рассуждая по-прежнему, мы получим:

или

Таким образом, алгебраическое выражение для конечной скорости остаётся без изменения. Изменяется только наименование скорости.
Следовательно, конечная скорость равноускоренного движения может быть рассчитана по формуле:

В этой формуле  —начальная скорость, а — ускорение и t—время.
—начальная скорость, а — ускорение и t—время.
Тот же результат можем получить алгебраически из формулы:

о которой говорится в параграфе 19.
Эта формула представляет собой уравнение первой степени. Решим его относительно 

отсюда

Для равноускоренного движения, которое начинается из состояния покоя,  поэтому из формулы (1) получим:
поэтому из формулы (1) получим:

Значит, если начальная скорость равна нулю, то мгновенная скорость равноускоренного движения пропорциональна времени.
Пользуясь формулой (3), можно значение вычисленных в опыте § 21 скоростей представить в виде следующей таблицы:

Из этой таблицы видно, что скорость движения шарика по наклонному жёлобу в любой момент времени может быть рассчитана но формуле:

График скорости равноускоренного движения

Рис. 36. Оси координат (ось времён и ось скоростей).
Зависимость скорости равноускоренного движения от времени можно выразить не только алгебраически, но и графически. Для этого возьмём две взаимно перпендикулярные оси координат (рис. 36). Одну из них Ov назовём осью скоростей, а другую Ot— осью времён. Перпендикуляр, опущенный из любой какой-нибудь точки А на ось времён, отсекает на ней отрезок ОВ, численно равный (в выбранном масштабе) некоторому промежутку времени t, а перпендикуляр, опущенный из той же точки на ось скоростей, отсекает отрезок ОС, рав
ный по величине скорости в конце этого промежутка времени.
Из построения видно, что расстояние АВ определяет величину скорости в момент времени t.
Построим сначала график движения без начальной скорости. Пусть, например, ускорение  По формуле
По формуле  рассчитаем скорость в конце первой секунды от начала движения, второй, третьей и т. д. и результаты запишем в таблицу.
рассчитаем скорость в конце первой секунды от начала движения, второй, третьей и т. д. и результаты запишем в таблицу.
Начертим оси координат Ov и Ot (рис. 37). На оси времён отложим равные отрезки 0—1. 1—2, 2—3 и т. д., каждый из которых соответствует 1 секунде.

Из концов этих отрезков по данным нашей таблицы (в масштабе 1 см— ) отложим мгновенные скорости в конце первой секунды, второй и т. д. Верхние концы A, В, С полученных отрезков соединим. Получим прямую, проходящую через начало координат и наклонённую к осям. Эта прямая и будет представлять собой график скорости равноускоренного движения.
) отложим мгновенные скорости в конце первой секунды, второй и т. д. Верхние концы A, В, С полученных отрезков соединим. Получим прямую, проходящую через начало координат и наклонённую к осям. Эта прямая и будет представлять собой график скорости равноускоренного движения.
График скорости равноускоренного движения имеет такой же вид, как и полученный нами ранее график пути равномерного движения (рис. 37).

Рис. 37. График скорости равноускоренного движения с начальной скоростью, равной нулю.

Рис. 38. График скорости равноускоренного движения с начальной скоростью, не равной нулю.
В обоих случаях график представляет собой прямую, проходящую через начало координат. Эго не случайное совпадение. Дело в том, что пройденный путь при равномерном движении и скорость при равноускоренном движении изменяются по одному и тому же закону—прямо пропорционально времени. Закон же прямой пропорциональности, как это доказывается в математике, графически изображается прямой линией.
Построим теперь график для случая, когда начальная скорость не равна нулю, например  и
и  Так же, как и в первом случае, но теперь по формуле
Так же, как и в первом случае, но теперь по формуле  рассчитаем скорость в конце первой секунды от начального момента отсчёта, в конце второй, третьей и т. д. Результаты запишем в таблицу.
рассчитаем скорость в конце первой секунды от начального момента отсчёта, в конце второй, третьей и т. д. Результаты запишем в таблицу.

Отмечая соответствующие точки на графике и соединяя их между собой линией, получим график скорости равноускоренного движения с начальной скоростью (рис. 38). Так как скорость увеличивается в каждую секунду на одну и ту же величину, то линия, соединяющая точки А, В, С, D,—прямая, но она не проходит через точку пересечения осей, так как в момент t = 0 скорость тела не равняется нулю.
Графический способ вывода формулы пути равноускоренного движения
В равномерном движении пройденный путь графически изображался площадью прямоугольника, построенного на графике скорости (§ 11).

Рис. 40. К выводу формулы пути, пройденного при равноускоренном движении.
В равноускоренном же движении с начальной скоростью пройденный путь изображается площадью трапеции. Это мы используем для вывода формулы пути равноускоренного движения.
На рисунке 40 график скорости равноускоренного движения изображён прямой АС. Путь, пройденный за время t, на том же рисунке изображается площадью ОАСВ; он численно равен площади ОАСВ. Эта площадь ограничена отрезком прямой АС, представляющим собой график скорости, отрезками 
Из рисунка 40 видно, что если к площади прямоугольника ОАМВ прибавить площадь треугольника АСМ, то мы получим площадь S фигуры ОАСВ. Таким образом,

Но OB = AM = t, 
 Отсюда для пройденного пути получим формулу:
Отсюда для пройденного пути получим формулу:
 или
или 
Для движения без начальной скорости  пройденный путь выразится формулой:
пройденный путь выразится формулой: 
По формуле  рассчитаем пройденные пути при равноускоренном движении за 1, 2, 3 и т. д. секунды для случая, когда ускорение равно
рассчитаем пройденные пути при равноускоренном движении за 1, 2, 3 и т. д. секунды для случая, когда ускорение равно  и полученные данные запишем в таблицу.
и полученные данные запишем в таблицу.

Из этой таблицы видно, что за две секунды тело пройдёт путь, в 4 раза больший, чем за первую секунду, за три секунды—в 9 раз больший и т. д., т.е. при равноускоренном движении без начальной скорости пройденный путь пропорционален квадрату времени.
Из формулы  и из приведенной таблицы следует, что путь, проходимый телом в первую секунду, численно равен половине ускорения. Если, например, поезд, двигаясь от станции, в первую секунду прошёл путь 1,5 м, то ускорение движения его
и из приведенной таблицы следует, что путь, проходимый телом в первую секунду, численно равен половине ускорения. Если, например, поезд, двигаясь от станции, в первую секунду прошёл путь 1,5 м, то ускорение движения его 
Средняя скорость равноускоренного движения
Из формулы пути равноускоренного движения легко вывести формулу средней скорости.
Из определения средней скорости следует (см. § 17), что  или
или  разделив каждое слагаемое числителя на t, получим:
разделив каждое слагаемое числителя на t, получим:

а преобразуя правую часть написанного равенства, будем иметь:
 или
или 
Так как  то получим:
то получим:

Итак, средняя скорость равноускоренного движения за некоторый промежуток времени равна полусумме начальной и конечной скоростей.
Для случая, когда 
В равноускоренном движении скорость движения изменяется равномерно от  до
до  Поэтому средняя скорость такого движения равна среднему арифметическому начальной и конечной скоростей:
Поэтому средняя скорость такого движения равна среднему арифметическому начальной и конечной скоростей:

Уравнения равноускоренного движения
Формулы

называются уравнениями равноускоренного движения; они выражают зависимость скорости или пути в этом движении от времени.
Этих формул вполне достаточно для решения любой задачи на равноускоренное движение. Однако для упрощения расчётов в задачах, где не дано времени движения, целесообразно пользоваться ещё одной формулой.
Из формулы ускорения (§ 19) время  Подставив его формулу
Подставив его формулу  получим:
получим:

Заменяя  её значением
её значением  и преобразуя полученное выражение, придём к формуле:
и преобразуя полученное выражение, придём к формуле:

откуда

или

Если начальная скорость равна нулю: то полученная формула (4) примет вид:
то полученная формула (4) примет вид:

или

Формулами (4) и (5) часто пользуются для решения задач, когда не дано времени движения.
Пути, проходимые в равноускоренном движении за равные последовательные промежутки времени
Воспользуемся таблицей пройденных путей, приведённой на странице 43, и определим пути, проходимые телом в равноускоренном движении без начальной скорости за каждую отдельную секунду.
Пройденный путь за первую секунду от начала движения равен  Обозначим его
Обозначим его 

Чтобы вычислить путь  за вторую секунду, надо из пути, пройденного за две секунды, вычесть путь, пройденный за первую секунду:
за вторую секунду, надо из пути, пройденного за две секунды, вычесть путь, пройденный за первую секунду:

Пройденный путь  за третью секунду найдём, вычитая из пути, пройденного за три секунды, путь, пройденный за две секунды:
за третью секунду найдём, вычитая из пути, пройденного за три секунды, путь, пройденный за две секунды:

Таким же образом найдём, что пути  пройденные за четвёртую и пятую секунды, будут равны:
пройденные за четвёртую и пятую секунды, будут равны:

Составим отношение из числовых значений пройденных путей:

Преобразуя правую часть равенства, получим:

Из полученного нами равенства видно, что пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечётных чисел.
Свободное падение тел
Одним из интересных и важных видов движения является движение падающих тел. Изучим это движение на опыте.

Рис. 43. Тело, подвешенное на нити, натягивает нить по вертикали.

Рис. 44.
Подвесим на нити какое-нибудь тяжёлое тело (рис. 43), нить натянется вдоль определённого направления. Это направление, как известно, называется вертикальным или отвесным, а нить с грузом—отвесом.
Если пережечь нить, тело будет падать по вертикальному направлению.
Выпустим из рук с одинаковой высоты одновременно плашмя металлический кружок и такого же диаметра лёгкий картонный кружок. Мы увидим, что скорее упадёт металлический кружок. Почему? Не является ли причиной этого различие в весе падающих тел?
Такой вывод легко опровергается следующим опытом. Возьмём два одинаковых листа бумаги и, скомкав один из них, уроним оба листа с одинаковой высоты. Мы увидим, что скомканный лист упадёт быстрее. Следовательно, причиной различной скорости падения тел является не только различие в весе тел.
Положим картонный кружок на металлический и выпустим их из рук. Оба кружка упадут в одно и то же время. Этот опыт отличается от первого тем, что условия падения кружков здесь неодинаковы. Металлический кружок, падая, встречает сопротивление воздуха, между тем как для картонного кружка этого препятствия нет: оно устраняется металлическим кружком, падающим впереди картонного. Следовательно, на скорость падения тел влияет сопротивление воздуха.
Рассмотрим теперь, как будут падать тела в отсутствие сопротивления воздуха, в безвоздушном пространстве.
Возьмём стеклянную трубку длиной примерно 1,5 м с одним закрытым концом и с краном на другом конце (рис. 44). В трубку вложены: монета, птичье пёрышко, кусочек пробки, дробинка, т. е. тела разной формы и разного веса. Пока в трубке имеется воздух, упомянутые тела при перевёртывании трубки движутся с разными скоростями. Но стоит только откачать воздух из трубки, и те же тела будут двигаться с одинаковыми скоростями.
Падение тел в безвоздушном пространстве называется свободным падением.

Галилео Галилей (1564— 1642)—великий итальянский учёный, основатель опытной физики.
Галилей открыл законы падения тел и качания маятника, ему принадлежит идея закона инерции, включённого Ньютоном в число основных законов механики. Галилей изобрёл термометр, первый применил телескоп для астрономических исследований, открыл спутников Юпитера, солнечные пятна и фазы Венеры.
Галилей был ревностным пропагандистом взглядов Коперника, за что был судим судом папской инквизиции и под угрозой пыток вынужден был подписать отказ от своих убеждений. Однако на деле он остался верен им и до конца жизни продолжал развивать учение о гелиоцентрической системе мира.
Падение тел опытным путём впервые изучал в конце XVI в. Галилей, роняя тяжёлые тела с башни (рис. 45). Эти опыты показали, что все тела, независимо от их веса, достигали поверхности земли почти в одно и то же время.

Рис. 45. Наклонная башня, которой пользовался Галилей для изучения законов падения тел.
Законы падения Галилей открыл, изучая движение шарика по наклонному жёлобу. Это движение является тоже падением, только протекающим медленнее, чем падение по вертикали.
Исследования Галилея показали, что свободное падение есть движение равноускоренное.
Особенностью свободного падения является то, что все тела в данном месте падают с одинаковым ускорением. Это ускорение называется ускорением свободного падения,
Ускорение свободного падения обозначается буквой (первая буква латинского слова гравитас, что значит тяжесть).
Так как движение свободно падающего тела есть равноускоренное движение без начальной скорости, то расчёты пути и скорости в этом движении производятся по формулам, выведенным в § 22 и 24.
Так, если тело падает с высоты h в течение времени t, то

При этом тело достигает скорости
v = gt или 
Величину g можно определить опытным путём, например заставляя стальной шарик падать с определённой высоты и измеряя время падения. Сопротивление воздуха, которое испытывает при этом шарик, незначительно.
При проведении одного такого опыта в пролёте школьной лестницы с высоты 17,6 м падал стальной шарик. Секундомер показал время падения 1,9 сек. По формуле  нашли, что
нашли, что 
Существуют, конечно, способы, позволяющие определить величину g значительно точнее, чем мы это делали в школе.
Численное значение g на разных широтах земного шара различно и колеблется между  на полюсах и
на полюсах и  на экваторе; для Москвы
на экваторе; для Москвы 
Ускорение свободного падения  называют нормальным.
называют нормальным.
Причины, вызывающие различие в ускорениях свободного падения тел, будут рассмотрены далее.
В расчётах, если не требуется особой точности, пользуются значением g, равным  или
или  или даже
или даже 
Равнозамедленное движение
На рисунке 47 изображено движение шарика от толчка вверх по наклонному жёлобу.

Рис. 47. Движение шарика вверх по наклонному жёлобу.
Флажками отмечены положения шарика через одну, две, три секунды от начала движения. Расстояние между флажками, а следовательно, и пути, проходимые шариком за равные промежутки времени, уменьшаются. Значит, движение шарика замедленное.
Простейшим видом замедленного движения является движение равнозамедленное.
В равнозамедленном движении скорость за любые равные промежутки времени уменьшается на одну и ту же величину.
При этом ускорение, вычисляемое по формуле:

окажется отрицательной величиной, так как  меньше
меньше  Пусть, например, скорость поезда при равнозамедленном движении за t= 10 сек. уменьшилась с
Пусть, например, скорость поезда при равнозамедленном движении за t= 10 сек. уменьшилась с  до
до  в таком случае ускорение
в таком случае ускорение

Равнозамедленное движение есть движение с постоянным отрицательным ускорением.
Чтобы получить формулы скорости и пути для равнозамедленного движения, достаточно в аналогичных формулах равноускоренного движения заменить а на — а.
Тогда формула скорости будет:

для пройденного же пути получим:

Равноускоренное и равнозамедленное движения часто называют равнопеременными движениями, так как в обоих этих движениях скорость изменяется равномерно.
Многие движения весьма близки к равнопеременным и при различных расчётах могут быть приняты за равнопеременные. Так, движения поездов и автомобилей при отходе их от остановки и при торможении, движение пули внутри ствола и многие другие могут рассматриваться как равнопеременные.
Движение тела, брошенного вертикально вверх
Примером замедленного движения (очень близкого к равнозамедленному) может служить движение тела, брошенного вертикально вверх.
Действительно всякое тело свободно падает с ускорением g, направленным вертикально вниз. Вследствие этого при движении тела вертикально вверх его скорость ежесекундно уменьшается на величину, численно равную ускорению свободного падения. Брошенное вертикально вверх тело движется равнозамедленно до тех пор, пока скорость его не станет равной нулю. В этот момент тело достигает наибольшей высоты и с этой высоты начинает свободно падать, двигаясь обратно вниз.
Формулы для подсчёта скорости и пути движения тела, брошенного вертикально вверх, для любого момента времени будут:

где h—высота, на которую поднимается тело за время t.
Формулу для расчёта высоты h можно также получить, рассматривая движение тела, брошенного вертикально вверх, как сложное движение, состоящее из двух движений: из движения равномерного, направленного вертикально вверх с некоторой начальной скоростью, и из свободного падения. Оба движения происходят по одной прямой; поэтому пройденный телом путь за некоторый промежуток времени будет равен алгебраической сумме путей, пройденных в каждом отдельном движении.
Обозначим скорость, с которой тело брошено вертикально вверх, через  Двигаясь только с этой скоростью равномерно, тело за t сек. могло бы подняться на высоту
Двигаясь только с этой скоростью равномерно, тело за t сек. могло бы подняться на высоту  Но оно одновременно, свободно падая, в течение того же времени t опускается вниз на расстояние
Но оно одновременно, свободно падая, в течение того же времени t опускается вниз на расстояние  Действительная высота h, на которую поднимается тело вверх за t сек., будет равна
Действительная высота h, на которую поднимается тело вверх за t сек., будет равна  или:
или:

Рассмотрим следующий пример. Пусть тело брошено вертикально вверх со скоростью  Для упрощения расчётов положим
Для упрощения расчётов положим  Определим, на какой высоте будет находиться тело через 3 сек. от начала движения. По формуле (2):
Определим, на какой высоте будет находиться тело через 3 сек. от начала движения. По формуле (2):

Так как в момент времени, когда тело достигает наибольшей высоты,  то время полёта определится из уравнения (1):
то время полёта определится из уравнения (1):
 отсюда
отсюда 
Чтобы определить наибольшую высоту, на которую поднимается тело, подставим найденную величину t в уравнение (2), определяющее h:

Найдём теперь, с какой скоростью тело, падая с этой высоты, вернётся к начальному своему положению. Так как тело, падая, будет двигаться равноускоренно без начальной скорости и пройдёт расстояние h, то скорость его будет равна:

т. е. скорость, с которой тело вернётся в то же место, откуда оно было брошено, равна первоначальной скорости (если не учитывать сопротивления воздуха).
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства газов
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
Рассмотрим падение шарика в вязкой жидкости
При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. При вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.
На шарик, падающий в вязкой жидкости, действуют три силы (рис. 2.2):
·  сила тяжести F1= mg = pш×V×g;
сила тяжести F1= mg = pш×V×g;
· сила Архимеда FА = pж×V×g (равная весу жидкости в объеме шарика);
· сила сопротивления, обусловленная вязкостью жидкости:
F = 6p×h×r×v,
где rш – плотность материала шарика;
rж – плотность жидкости;
V – объем шарика;
g – ускорение свободного падения.
Все три силы направлены по вертикали: F1 – вниз, F2 и F3 – вверх.
В общем случае уравнение движения шарика имеет вид
Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение dv/dt уменьшается до тех пор, пока шарик не достигнет такой скорости, при которой ускорение равно 0.
Тогда уравнение (2.3) примет вид:
в этом случае шарик движется с постоянной скоростью v0.
Решая (2.4) относительно h, получим
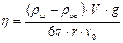 (2.5)
(2.5)
Если теперь учесть, что V =  r 3 , r = d/2, v0 = l/t,
r 3 , r = d/2, v0 = l/t,
где d – диаметр шарика;
l – длина участка равномерного движения, пройденного за время t,
то формула (2.5) примет окончательный вид
 (2.6)
(2.6)
Таким образом, для нахождения h нужно измерить d, l и t.
Рассмотрим подъем шарика в вязкой жидкости.
Если два одинаковых шарика связаны невесомой нитью, перекинутой через блок, причем один из шариков будет погружен в сосуд с жидкостью (2.3.), то уравнения движения шарика имеют вид:
 (2.7)
(2.7)
В уравнениях (2.7)
I – момент инерции диска;
R – радиус диска;
Т1 и Т2 – натяжение нитей,
Fтр – сила трения, обусловленная вязкостью жидкости,
FА – сила Архимеда.
Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается до тех пор, пока шарик не достигнет такой скорости v0, при которой ускорение равно 0.
Тогда уравнения (2.7), при  , принимают вид:
, принимают вид:


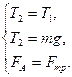
В этом случае шарик двигается с постоянной скоростью. Из (2.8) следует
 (2.9)
(2.9)
или аналогично формуле (2.6) расчетная формула принимает вид:
 (2.10)
(2.10)
В формуле (2.10) так же как и в формуле (2.6) нужно измерить d, l, t.
Описание установки.
Длинный стеклянный цилиндр, наполненный исследуемой жидкостью, имеет две горизонтальные метки А и В, расположенные на расстоянии l друг от друга. Метка А установлена так, что при прохождении через нее шарик уже имеет постоянную скорость v0 (см. рис 2.2).
При измерении вязкости при подъеме шарика применяется схема (рис. 2.3): на краю стеклянного цилиндра установлен блок, через который перекинуты шарики, связанные нитью. Для определения вязкости при подъеме шарика, один шарик опускают на дно цилиндра с жидкостью.
Ламинарное движение шарика в жидкости. Формула Стокса
Стоксом было получено строгое решение задачи о ламинарном обтекания шарика безграничной жидкостью. В этом случае сила сопротивления F определяется формулой
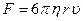 , (14)
, (14)
где h – коэффициент внутреннего трения жидкости, u –скорость шарика, r – радиус шарика.
Гидродинамический вывод формулы Стокса довольно сложен. Поэтому ограничимся анализом задачи с помощью теории размерности. На основании физических соображений и опыта можно считать, что сила F должна определяться параметрами h, u, r и плотностью жидкости rж. Искомый закон следует искать в виде степенного соотношения
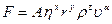 , (15)
, (15)
где А – безразмерный множитель, а x, y, z и a – подлежащие определению показатели степени. Выбор показателей степени определяется из того условия, что размерности левой и правой частей должны совпадать. Из опыта известно, сто при малых скоростях движения тела (ламинарное течение) сила сопротивления пропорциональна скорости (показатель степени a=1). Приравнивая показатели степени по массе, длине и времени в левой и правой частях уравнения (15), получим
1 = x + z, 1 = -x + 1 + y – 3z, -2 = -x – 1; (16)
x = 1, y = 1, z = 0. (17)
Таким образом получим
Безразмерный множитель А не может быть определен из соображения размерности, но строгое решение этой задачи дает для этого множителя значение 6p.
Рассмотрим свободное падение шарика в вязкой жидкости. На шарик действуют сила тяжести, архимедова сила и сила вязкого трения, зависящая от скорости u. На основании второго закона механики будем иметь
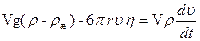 , (19)
, (19)
где V – объем шарика, r – его плотность, rж – плотность исследуемой жидкости, g – ускорение силы тяжести.
Решая это уравнение найдем
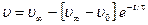 , (20)
, (20)
где 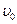 – скорость шарика в момент начала его движения, которая в опытах обычно равна нулю,
– скорость шарика в момент начала его движения, которая в опытах обычно равна нулю, 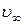 – установившаяся скорость движения шарика, t – время релаксации. При этом величины
– установившаяся скорость движения шарика, t – время релаксации. При этом величины 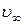 и t соответственно равны
и t соответственно равны
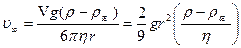 ;
; 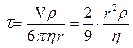 . (21)
. (21)
Из уравнения (20) видно, что скорость шарика экспоненциально приближается к установившейся скорости 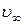 . Установление скорости определяется временем релаксации t. Если время падения шарика в несколько раз больше времени релаксации (t>>t), то процесс установления скорости можно считать закончившимся.
. Установление скорости определяется временем релаксации t. Если время падения шарика в несколько раз больше времени релаксации (t>>t), то процесс установления скорости можно считать закончившимся.
Поэтому для некоторой части пути, ограниченной метками А и В, где движение шарика будет равномерным, скорость шарика равна
где l – расстояние, t – время падения шарика между метками А и В.
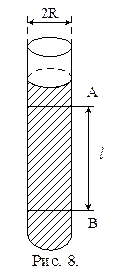 Подставляя значение скорости в уравнение (21), получим:
Подставляя значение скорости в уравнение (21), получим:
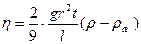 . (23)
. (23)
Данное уравнение справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиуса R, то приходится учитывать влияние стенок, т.е. ввести поправки на влияние боковых стенок. Формула для определения коэффициента вязкости с учетом поправок принимает следующий окончательный вид:
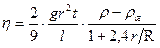 . (24)
. (24)
Соотношение (24) используется для определения вязкости жидкостей методом Стокса. Опуская шарик радиусом r в сосуд с исследуемой жидкостью, и измеряя время t прохождения шариком некоторого расстояния l можно найти коэффициент внутреннего трения жидкости h.
При выводе формулы Стокса предполагалось, что обтекание шарика жидкостью имеет ламинарный характер. Известно, что характер обтекания определяется значением числа Рейнольдса, которое определяется из формулы (6)
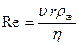 . (25)
. (25)
Для тел сферической формы обтекание будет ламинарным при условии Re
Дата добавления: 2015-12-16 ; просмотров: 5318 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
§ 1.3. Уравнение движения математического маятника
Рассмотрим простой маятник — шарик, подвешенный на длинной прочной нити. Если размеры шарика много меньше длины нити, то этими размерами можно пренебречь и рассматривать шарик как материальную точку. Растяжением нити также можно пренебречь, так как оно очень мало. Можно пренебречь и ее массой по сравнению с массой шарика. Таким образом, вместо реального маятника — шарика определенного размера на нити, которая, конечно, немного деформируется при движении и имеет массу, мы вправе рассматривать простую модель: материальную точку, подвешенную на нерастяжимой невесомой нити. Такая модель маятника называется математическим маятником в отличие от реального маятника, называемого физическим. Маленький шарик на длинной тонкой нити должен вести себя практически так же, как и математический маятник. Выведем маятник из положения равновесия и отпустим. На шарик будут действовать две силы: сила тяжести  = m
= m , направленная вертикально вниз, и сила упругости нити
, направленная вертикально вниз, и сила упругости нити  у, направленная вдоль нити (рис. 1.8).
у, направленная вдоль нити (рис. 1.8).

Конечно, при движении маятника на него еще действует сила трения. Но мы будем считать ее пренебрежимо малой.
Силу тяжести  удобно разложить на две составляющие: тангенциальную
удобно разложить на две составляющие: тангенциальную  τ, направленную по касательной к траектории перпендикулярно к нити, и нормальную
τ, направленную по касательной к траектории перпендикулярно к нити, и нормальную  n, направленную вдоль нити. Сила упругости нити
n, направленную вдоль нити. Сила упругости нити  у и составляющая силы тяжести
у и составляющая силы тяжести  п перпендикулярны к скорости маятника и сообщают ему нормальное ускорение. Действие этих сил не меняет скорости маятника по модулю, а приводит лишь к изменению направления скорости. Вектор скорости непрерывно поворачивается, так что в любой момент времени скорость направлена по касательной к дуге окружности — траектории маятника.
п перпендикулярны к скорости маятника и сообщают ему нормальное ускорение. Действие этих сил не меняет скорости маятника по модулю, а приводит лишь к изменению направления скорости. Вектор скорости непрерывно поворачивается, так что в любой момент времени скорость направлена по касательной к дуге окружности — траектории маятника.
Тангенциальная составляющая  τ силы тяжести создает тангенциальное ускорение, характеризующее изменение скорости по модулю. Она всегда направлена к положению равновесия, и именно она вызывает колебания маятника.
τ силы тяжести создает тангенциальное ускорение, характеризующее изменение скорости по модулю. Она всегда направлена к положению равновесия, и именно она вызывает колебания маятника.
При колебаниях шарика на нерастяжимой нити он всегда движется по дуге окружности, радиус которой равен длине нити l. Поэтому положение шарика в любой момент определяется одной величиной — углом α отклонения нити от вертикали (см. рис. 1.8). Будем считать угол α положительным, если маятник отклонен вправо от положения равновесия, и отрицательным, если он отклонен влево.
Уравнение для тангенциальной составляющей ускорения
Тангенциальная проекция силы тяжести в момент, когда нить маятника отклонена от положения равновесия на угол α, выражается так:

(Мы считаем значение проекции положительным, если составляющая силы направлена слева направо.) Знак «-» в уравнении (1.3.1) стоит из-за того, что  τ и α имеют противоположные знаки. При отклонении маятника вправо (α > 0) составляющая
τ и α имеют противоположные знаки. При отклонении маятника вправо (α > 0) составляющая  τ силы тяжести направлена влево и ее проекция отрицательна:
τ силы тяжести направлена влево и ее проекция отрицательна:  τ 0.
τ 0.
Согласно второму закону Ньютона

Разделив левую и правую части этого уравнения на m, получим:

До сих пор считалось, что углы отклонения нити от вертикали могут быть любыми, в дальнейшем будем считать их малыми. При малых углах, если выражать угол α в радианах, sin α ≈ α. Следовательно,

Смещение шарика маятника от положения равновесия можно характеризовать не только углом, но и величиной, измеряемой длиной дуги ОА (см. рис. 1.8), взятой со знаком «+», если шарик смещается от положения равновесия вправо, и со знаком «-», если он смещается влево. Очевидно, что

где s — длина дуги ОА.
Подставив в уравнение (1.3.4) это значение α, получим:


приходим к окончательному виду уравнения движения маятника при малых углах отклонения от положения равновесия:

Это уравнение имеет такой же вид, как и уравнение (1.2.6) движения шарика, прикрепленного к пружине. Здесь только вместо проекции ускорения аx стоит тангенциальное ускорение аτ и вместо координаты х — величина s. Да и  зависит уже не от жесткости пружины и массы груза, а от ускорения свободного падения и длины нити. Но по-прежнему ускорение прямо пропорционально смещению (определяемому дугой) шарика от положения равновесия. Если бы мы в случае маятника обозначили тангенциальное ускорение через аx, а дугу через х, то оба уравнения (1.2.6) и (1.3.8) были бы неразличимы.
зависит уже не от жесткости пружины и массы груза, а от ускорения свободного падения и длины нити. Но по-прежнему ускорение прямо пропорционально смещению (определяемому дугой) шарика от положения равновесия. Если бы мы в случае маятника обозначили тангенциальное ускорение через аx, а дугу через х, то оба уравнения (1.2.6) и (1.3.8) были бы неразличимы.
Важное заключение. Мы пришли к замечательному выводу: уравнения движения, описывающие колебания таких различных систем, как груз на пружине и маятник, одинаковы. Это означает, что движение шарика и колебания маятника происходят одинаковым образом. Смещения груза на пружине и шарика маятника от положения равновесия изменяются со временем по одному и тому же закону, несмотря на то, что силы, вызывающие колебания, имеют различную физическую природу. В первом случае это сила упругости, а во втором — составляющая силы тяжести.
Уравнение движения (1.2.6), как и уравнение (1.3.8), выглядит внешне очень просто: ускорение прямо пропорционально координате. Но решить его, т. е. определить, как меняется координата колеблющегося тела с течением времени, не просто. До сих пор в механике мы в основном рассматривали движение с постоянным ускорением. При колебаниях же ускорение меняется со временем, так как меняется сила, действующая на тело.
[spoiler title=”источники:”]
http://helpiks.org/6-19737.html
http://ansevik.ru/fizika-11/3.html
[/spoiler]
