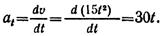Что такое равнозамедленное движение?
Равнозамедленное движение определение
Определение равнозамедленного движения:
Равнозамедленное движение – движение, при котором модуль (величина) скорости равномерно меняется, а вектор ускорения остаётся постоянным и по модулю, и по направлению.
Если укорение отрицательно, то модуль скорости равномерно уменьшается.
График скорости равнозамедленного движения
Пример графика скорости равнозамедленного движения, здесь начальная скорость равна 2 м/с, ускорение отрицательно и модуль его равен 0,3 м/с2:
(Этот график я построил с помощью построителя графиков. Выбрал в нём вид функции «Линейная: y = k * x + b» установил k = -0.3, b = 2 и нажал кнопку «Построить график».)
Чем больше отрицательное ускорение, тем быстрее будет падать скорость в нашем примере, т.е. если задать большее ускорение, то график круче пойдёт вниз.
Равнозамедленное движение формула
Формула скорости равнозамедленного движения (прямолинейного):
v = v0 — at
в этой формуле все величины являются скалярами, а не векторами.
Из формулы скорости равнозамедленного движения видно, что если увеличить ускорение, то быстрее будет падать скорость.
В момент времени t1 скорость падает до нуля, а после этого момента скорость нарастает, тело движется равноускоренно, но с отрицательной скоростью.
Формула закона равнозамедленного движения:
S = S0 + v0t — (at2)/2
Равнозамедленное движение. Формула равнозамедленного движения. График равнозамедленного движения
Что такое равнозамедленное движение?
Равнозамедленное движение определение
Определение равнозамедленного движения:
Если укорение отрицательно, то модуль скорости равномерно уменьшается.
График скорости равнозамедленного движения
Пример графика скорости равнозамедленного движения, здесь начальная скорость равна 2 м/с, ускорение отрицательно и модуль его равен 0,3 м/с 2 :
(Этот график я построил с помощью построителя графиков. Выбрал в нём вид функции «Линейная: y = k * x + b» установил k = -0.3, b = 2 и нажал кнопку «Построить график».)
Чем больше отрицательное ускорение, тем быстрее будет падать скорость в нашем примере, т.е. если задать большее ускорение, то график круче пойдёт вниз.
Равнозамедленное движение формула
Формула скорости равнозамедленного движения (прямолинейного):
в этой формуле все величины являются скалярами, а не векторами.
Из формулы скорости равнозамедленного движения видно, что если увеличить ускорение, то быстрее будет падать скорость.
В момент времени t1 скорость падает до нуля, а после этого момента скорость нарастает, тело движется равноускоренно, но с отрицательной скоростью.
Равнопеременное прямолинейное движение
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с. Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
= ‘
Проекция вектора скорости на ось ОХ: это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени: Учитывая, что 0 – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:
Отсюда формула скорости равнопеременного движения в любой момент времени: Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой: Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны: Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx
Графики прямолинейного движения
Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.
Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.
Будем отдельно рассматривать:
- движение без ускорения (равномерное), и
- движение с ускорением (неравномерное).
1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec =0).
2). Неравномерное движение — скорость меняется и появляется ускорение.
Пусть ускорение есть и, оно не изменяется: (vec =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:
- Равноускоренное движение — скорость тела увеличивается.
- Равнозамедленное движение — скорость уменьшается.
Примечание: Когда изменяется скорость, всегда появляется ускорение!
Движение будем изображать графически, используя две перпендикулярные оси.
На графиках будем откладывать:
- по горизонтали — время в секундах.
- по вертикали — координаты тела, или проекции скорости и ускорения.
Для каждого вида движения получим три графика. Графики будем называть так:
- x(t) – зависимость координаты от времени;
- v(t) – зависимость проекции скорости от времени;
- a(t) – зависимость проекции ускорения от времени.
Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.
Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют
Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_<0>) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_<0>]
Скорость и ускорение неподвижного тела равны нулю:
Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.
Скорость не меняется — движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка (x_<0>), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
[ x = x_ <0>+ v cdot t ]
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Равноускоренное движение в направлении оси, скорость увеличивается
Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.
Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.
Уравнение, которое описывает квадратичное изменение координаты, выглядит так:
Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:
[ v = v_ <0>+ a cdot t ]
Ускорение есть (рис. 4г) и оно не меняется:
Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.
Примечания:
1). Координата «x» будет изменяться:
- по линейному закону, когда скорость не меняется — остается одной и той же.
- по квадратичному закону, когда скорость будет изменяться (расти, или убывать).
2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.
3). Квадратичный закон – это уравнение второй степени, на графике — парабола.
4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.
Равноускоренное движение против оси
Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).
Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).
Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).
Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec) и (vec) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.
Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.
Скорость уменьшается — движение равнозамедленное
Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).
Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).
Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).
А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).
Равнозамедленное движение против оси
Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).
Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).
Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).
Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.
Выводы
1). Все, что лежит:
- выше оси t – положительное;
- ниже оси t – отрицательное;
- на горизонтальной оси t – равно нулю.
2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).
3). Если скорость не меняется, ускорения нет.
- График x(t) координаты – это прямая линия.
- График v(t) скорости – горизонтальная прямая.
- График a(t) ускорения лежит на оси t.
4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.
- График x(t) координаты – это правая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.
- График x(t) координаты – это левая ветвь параболы.
- График v(t) скорости – наклонная прямая.
- График a(t) ускорения – горизонтальная прямая.
[spoiler title=”источники:”]
http://www.av-physics.narod.ru/mechanics/rectilinear-movement.htm
[/spoiler]
Время, скорость, расстояние
О чем эта статья:
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой s.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути
Чтобы найти расстояние, нужно умножить скорость на время движения:
s = v × t
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.
Формула времени
Чтобы найти время, нужно разделить расстояние на скорость:
t = s : v
Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:
s = v × t = 50 × 15 = 750 (м)
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
Значит, скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.
Ответ: первый школьник добежал быстрее.
Если известны скорость и расстояние, то можно найти время: t = s : v.
Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:
t = s : v = 500 : 100 = 5 (мин)
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:
При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
За первую секунду тело переместится на расстояние, равное:
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:
Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду
Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:
Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x ( t ) = x 0 + v 0 t + a t 2 2 . .
Теперь мы можем выделить кинематические характеристики движения тела:
Перемещение тела определяется формулой:
s = v 0 t + a t 2 2 . .
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2
Кинетическая энергия тела определяется формулой:
Скорость при прямолинейном равноускоренном движении равна:
v = v 0 + a t = 5 − 6 t
Поэтому кинетическая энергия тела равна:
E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2
Следовательно, правильная последовательность цифр в ответе будет: 34.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Примеры решения задач
Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)

1. Вид движения: равнопеременное
2. При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчета – 10 м;
- начальная скорость 20 м/с;
- постоянное касательное ускорение at/2 = 5 м/с ; at= — 10 м/с .
- ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю:
v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.
Решение
1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).
Нормальное ускорение (ап = v 2 /r) при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.
2. На участке ВС:
— касательное ускорение равно нулю: at = 0;
— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение становится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.
3. На участке CD полное ускорение равно нулю.
Пример 3. По заданному графику скорости найти путь, пройденный за время движения (рис. 10.6).
Решение
1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).
Второй участок — равномерное движение: v = 8 м/с; a2 = 0.
Третий участок — торможение до остановки (равнозамедленное движение).
2. Путь, пройденный за время движения, будет равен:
Пример 4. Тело, имевшее начальную скорость 36 км/ч, прошло 50 м до остановки. Считая движение равнозамедленным, определить время торможения.
Решение
1. Записываем уравнение скорости для равнозамедленного движения:
Определяем начальную скорость в м/с: vо = 36*1000/3600 = 10 м/с.
Выразим ускорение (замедление) из уравнения скорости: a = — v0/t
2. Записываем уравнение пути: S = vot/2 + at 2 /2. После подстановки получим: S = vot/2
3. Определяем время до полной остановки (время торможения):
Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.
Решение
1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = at = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = at = —10 м/c 2 = const) с начальной скоростью v0 = 20 м/с.
2. Составим зависимость числовых значений s и v для первых 4 с движения
3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав масштабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Например, если расстояние s = 5 м изображать на графике длиной отрезка ls = 10 мм, то 5м = μs*10мм, где коэффициент пропорциональности μs и есть масштаб по оси Os : μs = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изображать на графике длиной lv =10 мм, то 10 м/c = μv * 10 мм и масштаб по оси Ov μv = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком la = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μa = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток времени Δt = 1 с отрезком μt = 10 мм, получим на всех графиках масштаб по осям Ot μt = 0,1 с/мм (0,1 с в 1 мм).
4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сторону).
За 4 с точка прошла путь so_4 = 40 м. Начав движение со скоростью v0 = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.
Если условно принять ускорение свободного падения g = 10 мс 2 и пренебречь сопротивлением воздуха, то можно сказать, что графики описывают движение точки, брошенной вертикально вверх со скоростью а0 = 20 м/с.
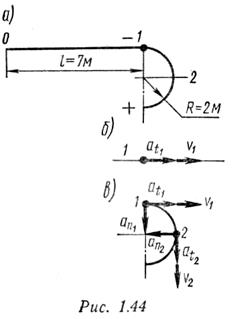
Решение
Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, определим из уравнения движения, подставив частные значения расстояния и времени:
Уравнение изменения скорости
Скорость точки в положении 1
Уравнение изменения касательного ускорения
Касательное ускорение точки в положении 1
Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Скорость и ускорение точки в конце этого участка траектории показаны на рис.1.44, б.
Определим скорость и ускорение точки в начале криволинейного участка траектории. Очевидно, что v1 = 11,5 м/с, аt1 = 14,2 м/с 2 .
Нормальное ускорение точки в начале криволинейного участка
Скорость и ускорение в начале криволинейного участка показаны на рис. 1.44, в (векторы at1 и aa1 изображены без соблюдения масштаба).
Положение 2 движущейся точки определяется пройденным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей центральному углу 90°:
Время, необходимое для перемещения точки из положения 0 в положение2,
Скорость точки в положении 2
Касательное ускорение точки в положении 2
Нормальное ускорение точки в положении 2
Ускорение точки в положении 2
Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и аПг изображены без соблюдения масштаба).

Решение
Уравнение изменения скорости
Время t1 определим из уравнения изменения скорости, подставив частные значения скорости и времени:
Определим положение точки на траектории в момент 3 с:
Дуга окружности длиной 135 м соответствует центральному углу
Уравнение изменения касательного ускорения
Касательное ускорение точки в момент tt
Нормальное ускорение точки в момент tt
Ускорение точки в момент tx
Скорость и ускорение точки в момент времени t1 показаны на рис. 1.45, б.
Как видно из рис. 1.45, б
Пример 8. В шахту глубиной H = 3000 м с поверхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверхности земли. Скорость звука 333 м/с.
Решение
Уравнение движения свободно падающего тела
Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравнения движения:
Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука
Время достижения звуком поверхности земли
Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли
Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и ускорение точки в момент времени t = 2 с.
Решение
Для определения траектории точки нужно из уравнений движения исключить параметр t — время.
Выразим t через х из первого уравнения:
и подставим это значение во второе уравнение:
Траекторией точки является парабола, симметричная относительно оси х.
Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям
Находим скорость точки
При t = 2 с получаем
Находим составляющие ускорения точки
Контрольные вопросы и задания
1. Запишите формулу ускорения при прямолинейном движении.
2. Запишите формулу ускорения (полного) при криволинейном движении.
3. 
4. Параметры движения не меняются.
4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движения точки, ответьте, чему равны начальная скорость и ускорение.
5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.
6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).
7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).
источники:
http://spadilo.ru/peremeshhenie-i-put-pri-ravnouskorennom-pryamolinejnom-dvizhenii/
http://mydocx.ru/12-105317.html
Понятия и пояснения
Тормозной путь — это путь, который проходит автомобиль с момента, когда сработал тормозной механизм до полной остановки автомобиля. На него влияют:
- состояние и тип дорожного покрытия,
- состояние шин автомобиля,
- начальная скорость автомобиля,
- масса автомобиля,
- исправность тормозной системы.
Остановочный путь — путь с момента обнаружения опасности до полной остановки автомобиля. Понятно, что тормозной путь входит в остановочный. Кроме того в остановочный путь входят:
- путь, который проехал автомобиль с момента обнаружения опасности до нажатия на педаль тормоза;
- путь, пройденный автомобилем за время срабатывания тормозной системы.
Первый параметр зависит от множества факторов, определяющим из которых является времени реакции водителя. По результатам многочисленных экспериментов, оно может меняться от 0,3 до 1,5 секунды. В среднем можно считать время реакции водителя равное 1 секунде. Кроме этого существует понятие «нормативное время восприятия сложной ситуации» равное 0,8 секунды. Также установлено, что время реакции у женщин, при возникновении сложной дорожной ситуации может достигать 2,5-3 секунд, тогда как у мужчин 1,5-2 секунды. Кроме этого на время реакции влияет:
- опыт водителя,
- его эмоциональное состояние,
- возраст,
- время суток и погодные условия,
- прием медикаментов,
- состояние алкогольного или иного опьянения,
- место возникновения опасной ситуации.
Время срабатывания тормозной системы зависит от ее типа и технического состояния. Тормозная система с гидравлическим приводом срабатывает за 0,2 – 0,3 секунды, с пневматическим за 0,5 –0,6 секунд.
Бесплатная программа для расчёта скорости и тормозного пути
Как определить скорость автомобиля и тормозной путь?
Ниже рассматривается небольшая бесплатная программка для расчёта тормозного пути автомобиля при известной скорости и наоборот (можно рассчитать скорость при известном тормозном пути).
Тормозной путь — это расстояние, проходимое транспортным средством от момента привода в действие тормозного устройства до полной остановки.
Полный тормозной путь включает в себя также расстояние, проходимое за время от момента восприятия водителем (машинистом) необходимости торможения до приведения в действие органов управления тормозами.
Длина тормозного пути пропорциональна квадрату скорости движения, быстроте срабатывания тормозов, нагрузке, приходящейся на затормаживаемые колёса, коэффициенту сцепления колёс с дорогой, а также зависит от реакции водителя. Длина тормозного пути зависит от состояния тормозной системы, скорости движения автомобиля, состояния дороги, а также от состояния и качества шин. При увеличении скорости движения автомобиля, например в 2 раза, тормозной путь возрастает примерно в 4 раза. На мокрой дороге тормозной путь легкового автомобиля увеличивается по сравнению с сухой дорогой в 2 раза, а на заснеженной и обледеневшей поверхности дороги – примерно в 4 раза. Остановочный путь включает тормозной путь, а также расстояние, которое проходит автомобиль за время реакции водителя (от осознания опасности до начала нажатия на педаль тормоза). Отрезок пути, который проходит автомобиль за время реакции водителя, автомобиль движется с неизменной скоростью.
Как определить скорость автомобиля по тормозному пути?
Равнозамедленное движение: v х v/2=Sa,
где v — скорость до начала торможения,
S-пройденный путь (длина черного следа резины размазанной по асфальту),
a-ускорение (замедление) в торможении.
Это берется из перехода ВСЕЙ кинетической энергии в работу силы трения (разрушение резины, т.е. черный след). Значение коэффициента сцепления может быть от 0.7-0.9 для сухого асфальта и хорошей резины до 0.03-0.01 на льду. Умелое торможение на грани блокировки колес (работа хорошей АБС) могут повысить коэффициент трения процентов на 10-20, но это не наш случай: раз черный след на асфальте — колеса были заблокированы. Минимально допустимая эффективность тормозов для легковушки 0.64 (на каждую тонну веса тормозное усилие 640 кг) регламентируется в ГОСТ 25478-91 для вообще тормозов. Предполагается что на сухом асфальте (или на резине барабана на ПИК) сцепление резины гораздо лучше, так что это качество собственно тормозов. В остановочный путь еще входит расстояние пройденное с начальной скоростью за время реакции водителя (0.2 сек) и время срабатывания тормозной системы (по ГОСТ 25478-91 не хуже 0.5 сек для легковушек). Черного следа на асфальте в это время не остается, и в расчетах скорости из длины тормозного следа поэтому используют только тормозной путь.
Чем отличается тормозной путь от остановочного?
Тормозной и остановочный пути – это разные понятия, которые часто путают или принимают за одно и тоже.
Остановочный путь – это расстояние, которое прошло транспортное средство с момента осознания автомобилистом необходимости в остановки до достижения машиной скорости 0 км/ч.
А тормозной путь – это дистанция, которую прошла машина с момента срабатывания ее тормозов до ее остановки.
Таким образом, остановочное расстояние включает в себя не только дистанцию торможения, но и расстояние, которое прошло транспортное средство, пока автомобилист реагировал на дорожную ситуацию.
Формулы расчёта скорости по тормозному пути
После дорожно-транспортного происшествия фактический тормозной путь автомобиля измеряется сотрудниками ГИБДД или следователем путём фиксации следа шин на асфальте, и занесения данных в специальную расчётную таблицу. Учитываются несколько факторов:
- вид т/с;
- масса машины в момент, когда произошло ДТП;
- характер покрытия дороги и его состояние.
Прежде всего, нужно быстро установить скорость, с которой двигался автомобиль до торможения. Она рассчитывается следующим образом
Ускорение свободного падения является физической константой, и не изменяется, в какой бы формуле его величина не использовалась. Скорость из км/ч необходимо перевести в м/с, в соотношении 36 к 10: 36 км/ч = 10 м/с. По ГОСТ 25478-91 допустимый минимум эффективности тормозной системы автомобиля составляет 0,64. Это означает, что на тонну веса автотранспортного средства должно приходиться тормозное усилие не менее 640 кг.
Главный фактор, влияющий на точность расчёта
Единственной изменяемой величиной в формуле определения скорости является длина тормозного пути. Ручной расчёт данной величины в идеальных условиях (движение со скоростью 60 км/ч по сухой дороге асфальтовым покрытием, торможение без заносов) можно произвести по формуле
v – скорость движения автомобиля вначале торможения, м/с;
μ – коэффициент трения;
g – ускорение свободного падения, м/с2.
Другая формула для проверки правильности первоначального расчёта
Кэ – величина тормозного коэффициента;
V – скорость в момент начала торможения;
Фс – величина коэффициента сцепления шин с дорожным покрытием (при сухой погоде – 0,7, в дождливую погоду – 0,4; в снег – 0,2; в гололёд – 0,1).
Так, при движении по сухой асфальтовой трассе со скоростью 60 км/ч длина тормозного пути составит S = 1*60*60/(254*0,7) = 20,25 м. При движении по льдистой трассе, на которой Фс падает с 0,7 до 0,1, величина S увеличится в 7 раз (141,7 м).
Таким образом, главной задачей для правильного вычисления скорости является определение величины остановочного пути. В его состав, кроме, собственно, тормозного пути, входит метраж, приходящийся на:
- время реакции водителя (0,2 с);
- время срабатывания системы торможения (0,5 с).
Автомобиль при этом движется с начальной (фактической) скоростью, а следа от шин на дороге не остаётся.
Когда и как производится замер
Расчет тормозного пути может потребоваться в следующих случаях:
- технические испытания транспортного средства;
- проверка возможностей машины после доработки тормозов;
- криминалистическая экспертиза.
Как правило, при расчете используют формулу S=Кэ*V*V/(254*Фс). Здесь S – тормозной путь; Кэ – тормозной коэффициент; V₀ — скорость на момент начала торможения; Фс – коэффициент сцепления с покрытием.
Коэффициент сцепления с дорогой изменяется в зависимости от состояния покрытия и определяется по следующей таблице:
| Состояние дороги | Фс |
| Сухая | 0.7 |
| Мокрая | 0.4 |
| Снег | 0.2 |
| Лед | 0.1 |
Коэффициент Кэ является статической величиной и составляет единицу для всех наиболее распространенных легковых транспортных средств.
Пример: как рассчитать тормозной путь автомобиля при цифре 60 км/ч на спидометре в дождь? Дано: скорость 60 км/ч, тормозной коэффициент – 1, коэффициент сцепления – 0.4. Считаем: 1*60*60/(254*0.4). В итоге получаем цифру 35.4, что и является длиной тормозного пути в метрах.
В таблице указано сколько метров машина будет продолжать движение до полной остановки. Следует учитывать, что в расчет не берутся никакие иные показатели (повороты, выбоины на дороге, встречный поток и т.д.). Сомнительно, что в реальных условиях на обледенелой дороге, автомобиль сможет проскользить километр и не встретить столб или отбойник.
Расчёт скорости при экспертизе
Для экспертного определения начальной скорости движения машины специалистами используется формула:
Va = 0,5*tз*j + √2Sю*j,
tз – время, в течение которого скорость движения автомобиля замедляется, с;
j – константа замедления в момент торможения, м/с2 (определяется справочным путём, на основании ГОСТ 25478-91);
Sю – протяжённость следа при торможении, м.
На сухой дороге j равен 6,8 м/с2, поэтому скорость заноса тормозящего на расстоянии в 21 метр автомобиля равна 64,5 км/ч.
После начала реагирования водителя на окружающую обстановку машина до полного обнуления скорости проходит так называемый остановочный путь
Sо = (S1 + S2 + S3 + S4) = (t1 + t2 + 0,5*t3)*Va + Va/2j,
t1 – реакция водителя;
t2 – запаздывание гидропривода тормозной системы;
tз – нарастание замедления.
Временной промежуток t4 (время полной остановки) рассчитывается как отношение скорости заноса Vю к замедлению j. Время, пока увеличивается скорость замедления, зависит от трёх показателей:
- тип привода;
- состояние покрытия дороги;
- масса транспортного средства.
Для его определения из начальной скорости Vа следует вычесть половину до установления минимальной скорости tз*j. Таким образом, суммарное время динамической части ДТП для автомобиля составляет t0 = t1 + t2 + t3 + t4 = Т + Va/j, с.
Внимание! Время увеличения замедления для пневмопривода больше, нежели для гидравлического. Оно возрастает с увеличением снаряжённой массы машины и коэффициента сцепления
Дистанция
- Три длины автомобиля. Любой, кто путешествует в городских условиях, должен соблюдать дистанцию не менее 15 метров, или три длины автомобиля.
- Половина спидометра: для безопасной дистанции за пределами населенных пунктов обращайте внимание на скорость автомобиля. Для того чтобы вычислить безопасную дистанцию, разделите на 2 текущую скорость, которую показывает спидометр. В итоге вы получите дистанцию до других автомобилей в метрах. Пример: на скорости 70 км/ч вы должны держаться до впереди идущего автомобиля на расстоянии не менее 35 метров. Причем это касается сухого асфальта в летнее время.
- Двойное расстояние: в случае плохой видимости или плохих дорожных условий вы должны удвоить безопасную дистанцию.
Без этого не обойтись при проведении расчётов
Ещё один важный показатель – протяжённость заноса (юза) при торможении Sю. Это отношение квадрата скорости юза к удвоенной константе замедления j. Такой след заблокированные колодками колёса машины начинают оставлять на дорожном покрытии при положении «педаль в пол». Начало следа – это точка установившегося замедления, то есть константы. Как уже было сказано выше, это экспериментальная величина. Она рассчитывается для каждого вида транспорта отдельно. При этом используется физическая формула
Продольное сцепление резины с дорожным покрытием f замеряется эмпирически, с помощью «пятого колеса» или специальных приборов.
На основании специальной таблицы время реакции водителя на ситуацию на дороге составляет 0,6-1,4 секунд (шаг 0,2). Усреднённая экспертная величина, которая применяется в официальных экспертизах , составляет 0,8 с (в связи с тем, что быстрее этого времени человеческий мозг среагировать на происходящее не в состоянии).
Чтобы упростить восприятие производимых математических расчётов, сделаем привязку величины остановочного пути к скорости автомобиля длиной 4 м. Привязка делается к скорости 64 км/ч, с шагом ½ в сторону её замедления и увеличения:
Три способа определить скорость автомобиля при ДТП
После каждого дорожно-транспортного происшествия обязательно определяется скорость транспортного средства до и в момент удара или наезда. Данная величина имеет столь большое значение по нескольким причинам:
- Самый часто нарушаемый пункт правил дорожного движения именно превышение максимально допустимой скорости движения, и, таким образом, становиться возможным определить вероятного виновника ДТП.
- Также скорость влияет на тормозной путь, а значит и на возможность избежать столкновения или наезда.
Дорогой читатель! Наши статьи рассказывают о типовых способах решения юридических вопросов, но каждый случай носит уникальный характер.
Если вы хотите узнать, как решить именно Вашу проблему — обращайтесь в форму онлайн-консультанта справа или звоните по телефону.
Это быстро и бесплатно !
Определение скорости автомобиля по тормозному пути
Под тормозным путём обычно понимают расстояние, которое проходит то или иное транспортное средство от начала торможения (или, если быть более точным, с момента активации тормозной системы) и до полной остановки. Общая, недетализированная формула, из которой возможно вывести формулу для расчета скорости, выглядит так:
Va = 0.5 х t3 х j + √2Sю х j = 0,5 0,3 5 + √2 х 21 х 5 = 0,75 +14,49 = 15,24м/с = 54,9 км/ч где: в выражении √2Sю х j, где:
- Va – начальная скорость автомобиля, измеряемая в метрах в секунду;
- t3 – время нарастания замедления автомобиля в секундах;
- j – установившееся замедление автомобиля при торможении, м/с2; обратите внимание, что для мокрого покрытия – 5м/с2 по ГОСТ 25478-91, а для сухого покрытия j=6,8 м/с2, отсюда начальная скорость автомобиля при “юзе” в 21 метр равна 17,92м/с, или 64,5км/ч.
- Sю – длина тормозного следа (юза), измеряемая так же в метрах.
Дистанция
- Три длины автомобиля. Любой, кто путешествует в городских условиях, должен соблюдать дистанцию не менее 15 метров, или три длины автомобиля.
- Половина спидометра: для безопасной дистанции за пределами населенных пунктов обращайте внимание на скорость автомобиля. Для того чтобы вычислить безопасную дистанцию, разделите на 2 текущую скорость, которую показывает спидометр. В итоге вы получите дистанцию до других автомобилей в метрах. Пример: на скорости 70 км/ч вы должны держаться до впереди идущего автомобиля на расстоянии не менее 35 метров. Причем это касается сухого асфальта в летнее время.
- Двойное расстояние: в случае плохой видимости или плохих дорожных условий вы должны удвоить безопасную дистанцию.
Автоликбез 14 сентября 2019
Каждому водителю важно помнить, что его машина не может остановиться мгновенно. Для этого ему потребуется определенное время, на которое влияет большое количество факторов. Правила дорожного движения требуют соблюдать безопасное расстояние между собственным и впереди идущим автомобилем, чтобы в случае необходимости успеть затормозить. Чтобы знать величину этого расстояния, необходимо иметь представление о тормозном пути. Помимо этого, многие путают два понятия – тормозной и остановочный путь.
Определение скорости автомобиля исходя из полученных деформаций
- конструкция каждого конкретного автомобиля;
- особенности распределения грузов;
- срок эксплуатации автомобиля;
- количества и качества пройденных транспортным средством кузовных работ;
- старение метала;
- модификации конструкции автомобиля.
Определение скорости в момент наезда (столкновения)
Скорость в момент наезда обычно определяют по тормозному следу, но если это по ряду причин не представляется возможным, то приблизительные цифры скорости можно получить анализируя травмы, полученные пешеходом, и повреждения, образовавшиеся после наезда на транспортном средстве.
К примеру, о скорости автомобиля можно судить по особенностям бампер-перелома – специфической для наезда автомобилем травмы, которая характеризуется наличием поперечно-осколочного перелома с крупным отломком кости неправильной ромбообразной формы на стороне удара. Локализация при ударе бампером легкового автомобиля – верхняя или средняя треть голени, для грузового автомобиля – в участке бедра.
Что подразумевается под тормозным путем?
Это отрезок по прохождению машины с момента выявления препятствий и до остановки авто. При этом, когда водитель увидел препятствие и нажал на тормоз, прошло еще какое-то количество времени. Полнота тормозного пути немного увеличена.
На определение скорости по тормозному пути (на длину) влияют:
- Тормозной механизм.
- Имеет основную тормозную систему.
- Стояночную систему.
- Вспомогательную.
- Шинный протектор. Зачастую торможение зависит от изношенности шины. Они разрушаются солнцем и озоном. Это также нужно учитывать.
- Дорожное покрытие и то, в каком оно состоянии находится.
- Скоростной фактор движения машины.
- Массовый фактор машины.
- Дистанционная особенность.
От тормозов машины целиком зависит и снижаемость скорости до его останавливания. Нужно сохранять устойчивое и управляемое свойство машины. И главный фактор, влияющий на определение скорости по тормозному пути, ― водительский стаж того, кто управляет ТС.
Аккредитованная независимая экспертная организация АНО Центр Экспертизы Двигателей, имеющая лицензионные документы, проводит различные методики и проверки автомобильных экспертиз. Квалифицированные специалисты проведут ряд анализов и проверок по вашим данным. Обратившись, вы получите ответы на все интересующие вас вопросы. А в конце проверки вам выдадут заключение с выводами экспертов.
Анализ методов определения скорости автомобиля при ДТП
По тормозному следу
Достоинства:
- относительная простота метода;
- большое количество научных работ и составленных методических рекомендаций;
- достаточно точный результат;
- возможность быстрого получения результатов экспертизы.
Недостатки:
- при отсутствии следов шин (если автомобиль, к примеру, не тормозил перед столкновением, или особенности дорожного покрытия не позволяют с достаточной достоверностью измерить след юза) проведение данного метода невозможно;
- не учитывается воздействие одного транспортного средства в ходе столкновения на другое, что может.
По закону сохранения количества движения
Преимущества:
- возможность определения скорости транспортного средства даже при отсутствии следов торможения;
- при тщательном учёте всех факторов метод имеет высокую достоверность результата;
- удобство использования метода при перекрёстных столкновениях и столкновениях с неподвижными автомобилями.
Недостатки:
- отсутствие данных о режиме движения транспортного средства приводит к неточному результату;
- по сравнению с предыдущим методом более сложные и громоздкие вычисления;
- метод не учитывает энергию, затраченную на образование деформаций.
Три способа определить скорость автомобиля при ДТП
После каждого дорожно-транспортного происшествия обязательно определяется скорость транспортного средства до и в момент удара или наезда. Данная величина имеет столь большое значение по нескольким причинам:
Определение скорости автомобиля по тормозному пути
Под тормозным путём обычно понимают расстояние, которое проходит то или иное транспортное средство от начала торможения (или, если быть более точным, с момента активации тормозной системы) и до полной остановки. Общая, недетализированная формула, из которой возможно вывести формулу для расчета скорости, выглядит так:
Va = 0.5 х t3 х j + √2Sю х j = 0,5 0,3 5 + √2 х 21 х 5 = 0,75 +14,49 = 15,24м/с = 54,9 км/ч где: в выражении √2Sю х j, где:
Исходя из указанного выше уравнения, можно сделать вывод, что на тормозной путь влияет в первую очередь скорость автомобиля, которую при известных остальных величинах нетрудно вычислить. Наиболее сложной частью вычислений по этой формуле является точное определение коэффициента трения, так как на его значение влияет целый ряд факторов:
Для точного результата расчётов также нужно принимать во внимание особенности тормозной системы конкретного транспортного средства, например:
Тормозной след
После достаточно быстрой активации тормозной системы на дорожном покрытии остаются отпечатки – тормозные следы. В случае если колесо во время торможения заблокировано полностью и не вращается, остаются сплошные следы, (которые иногда называют «след юза») которые многие авторы призывают считать следствием максимально возможного нажатия на педаль тормоза («тормоз в пол»). В случае же когда педаль нажата не до конца (или присутствует какой-либо дефект тормозной системы) на дорожном покрытии остаются как бы «смазанные» отпечатки протектора, которые образуются вследствие неполной блокировки колес, которые при таком торможении сохраняют возможность вращаться.
Остановочный путь
Остановочным путём считают то расстояние, которое проходит определённое транспортное средство начиная с обнаружения водителем угрозы и до остановки автомобиля. Именно в этом заключается главное отличие тормозного пути и остановочного пути – последний включает в себя и расстояние, которое преодолел автомобиль за время срабатывания тормозной системы, и расстояние, которое было преодолено за время, понадобившееся водителю на осознание опасности и реакции на нее. На время реакции водителя влияют такие факторы:
Определение скорости исходя из закона сохранения количества движения
Возможно также и определение скорости движения автомобиля по характеру его перемещения после столкновения, а также, в случае столкновения с другим транспортным средством, по перемещению второй машины в результате передачи кинетической энергии от первой. Особенно часто данный метод используют при столкновениях с неподвижными транспортными средствами, или если столкновение случилось под углом, близким к прямому.
Определение скорости автомобиля исходя из полученных деформаций

Это связано с огромным количеством факторов, влияющих на образование повреждений, а также с тем, что некоторые факторы попросту невозможно учесть. Оказывать влияние на образование деформаций могут:
Определение скорости в момент наезда (столкновения)
Скорость в момент наезда обычно определяют по тормозному следу, но если это по ряду причин не представляется возможным, то приблизительные цифры скорости можно получить анализируя травмы, полученные пешеходом, и повреждения, образовавшиеся после наезда на транспортном средстве.
К примеру, о скорости автомобиля можно судить по особенностям бампер-перелома – специфической для наезда автомобилем травмы, которая характеризуется наличием поперечно-осколочного перелома с крупным отломком кости неправильной ромбообразной формы на стороне удара. Локализация при ударе бампером легкового автомобиля – верхняя или средняя треть голени, для грузового автомобиля – в участке бедра.
Анализ методов определения скорости автомобиля при ДТП
По тормозному следу
Достоинства:
Недостатки:
По закону сохранения количества движения
Преимущества:
Недостатки:
Исходя из полученных демормаций
Преимущества:
Недостатки:
На практике чаще всего используют два метода – определение скорости по следу торможения и исходя из закона сохранения количества движения. При использовании двух этих методов одновременно обеспечивается максимально точный результат, так как методики дополняют друг друга.
Остальные способы определения скорости транспортного средства значительного распространения не получили по причине недостоверности получаемых результатов и/или необходимости громоздких и сложных вычислений. Также при оценке скорости автомобиля учитывают показания свидетелей происшествия, хотя в таком случае нужно помнить о субъективности восприятия скорости разными людьми.
В некоторой мере помочь разобраться с обстоятельствами происшествия и в итоге получить более точный результат может помочь анализ видео из камер наблюдения и видеорегистраторов.
Источник
Калькулятор определение скорости автомобиля по тормозному пути


Определение скорости автомобиля по тормозному пути
Под тормозным путём обычно понимают расстояние, которое проходит то или иное транспортное средство от начала торможения (или, если быть более точным, с момента активации тормозной системы) и до полной остановки. Общая, недетализированная формула, из которой возможно вывести формулу для расчета скорости, выглядит так:
Va = 0.5 х t3 х j + √2Sю х j = 0,5 0,3 5 + √2 х 21 х 5 = 0,75 +14,49 = 15,24м/с = 54,9 км/ч где: в выражении √2Sю х j, где:
Исходя из указанного выше уравнения, можно сделать вывод, что на тормозной путь влияет в первую очередь скорость автомобиля, которую при известных остальных величинах нетрудно вычислить. Наиболее сложной частью вычислений по этой формуле является точное определение коэффициента трения, так как на его значение влияет целый ряд факторов:
Для точного результата расчётов также нужно принимать во внимание особенности тормозной системы конкретного транспортного средства, например:
Тормозной след
После достаточно быстрой активации тормозной системы на дорожном покрытии остаются отпечатки – тормозные следы. В случае если колесо во время торможения заблокировано полностью и не вращается, остаются сплошные следы, (которые иногда называют «след юза») которые многие авторы призывают считать следствием максимально возможного нажатия на педаль тормоза («тормоз в пол»). В случае же когда педаль нажата не до конца (или присутствует какой-либо дефект тормозной системы) на дорожном покрытии остаются как бы «смазанные» отпечатки протектора, которые образуются вследствие неполной блокировки колес, которые при таком торможении сохраняют возможность вращаться.
Остановочный путь
Остановочным путём считают то расстояние, которое проходит определённое транспортное средство начиная с обнаружения водителем угрозы и до остановки автомобиля. Именно в этом заключается главное отличие тормозного пути и остановочного пути – последний включает в себя и расстояние, которое преодолел автомобиль за время срабатывания тормозной системы, и расстояние, которое было преодолено за время, понадобившееся водителю на осознание опасности и реакции на нее. На время реакции водителя влияют такие факторы:
Понятие тормозного пути автомобиля
Тормозной путь — это расстояние, проходимое автомобилем от начала торможения (момента срабатывания привода) и до полной остановки.
Какие факторы влияют на тормозной путь?
Жизнь человека бесценна. В экстренной ситуации (ДТП) тормозной путь является решающим фактором, который нельзя игнорировать. Потому что каждый метр может стоить жизни.
Изучите факторы, которые влияют на тормозной путь. Эти знания помогут сохранить здоровье и избежать ДТП:
1) Состояние автомобильных шин. Шины являются одним из наиболее важных элементов колеса. В процессе движения транспортного средства они обеспечивают безопасность.
При выборе шины необходимо обратить внимание на высоту протектора. Что такое протектор? Это элемент шины. Он защищает шину от повреждений, а также проколов. Правильно выбранные шины обеспечат хорошее управление машиной.
Показатель сцепления ТС с дорогой напрямую зависит от технического состояния протектора. На рынке представлен большой ассортимент покрышек. Глубина протектора составляет 5–17 мм.
При этом нужно разделять зимние и летние шины:
По результатам проведённых экспериментов было выяснено, что при износе протектора значительно увеличивается тормозной путь машины. В процессе эксплуатации протектор изнашивается. Поэтому значительно уменьшается сила трения.
В зимнее время обязательно используйте только зимние шины. Тогда как в летнее время —летние шины. В таком случае вы обеспечите оптимальное управление машиной. Для изготовления зимних шин используют специальную мягкую резину.
Такие изделия имеют глубокие канавки, а также ребристый рисунок. Данные особенности обеспечивают превосходное сцепление в зимнее время года. А для изготовления летних шин используют жёсткую резину.
2) Состояние тормозной системы. Это система предназначена для остановки автомобиля, а также для снижения скорости движения. Это одна из самых важных систем в машине. Потому что она обеспечивает безопасность.
Рассмотрим пункт 2.3.1. ПДД. Запрещается передвижение автомобиля с неисправными тормозами. Неисправность этой системы приводит к потере эффективности торможения транспортного средства.
Обязательно нужно учитывать время срабатывания этой системы. Согласно требованиям, время срабатывания не более 0,6 с.
Рассмотрим факторы, которые влияют на время срабатывания:
Длина тормозного пути зависит от времени срабатывания этой системы.
3) Начальная скорость транспортного средства. Чем выше ваша скорость, тем длиннее будет путь.
4) Покрытие дороги.
5) Состояние машины.
6) Погодные условия.
7) Способ торможения:

Определение скорости автомобиля исходя из полученных деформаций

Лишь очень незначительное количество экспертов определяют скорость движения автомобиля таким способом. Хотя зависимость повреждений автомобиля от его скорости и очевидна, но единой эффективной, точной и воспроизводимой методики определения скорости по полученным деформациям не существует.
Это связано с огромным количеством факторов, влияющих на образование повреждений, а также с тем, что некоторые факторы попросту невозможно учесть. Оказывать влияние на образование деформаций могут:
Определение скорости в момент наезда (столкновения)
Скорость в момент наезда обычно определяют по тормозному следу, но если это по ряду причин не представляется возможным, то приблизительные цифры скорости можно получить анализируя травмы, полученные пешеходом, и повреждения, образовавшиеся после наезда на транспортном средстве.
К примеру, о скорости автомобиля можно судить по особенностям бампер-перелома – специфической для наезда автомобилем травмы, которая характеризуется наличием поперечно-осколочного перелома с крупным отломком кости неправильной ромбообразной формы на стороне удара. Локализация при ударе бампером легкового автомобиля – верхняя или средняя треть голени, для грузового автомобиля – в участке бедра.
Расчет максимальной скорости автомобиля
Это будет не информационный пост как обычно, а некий мануал, калькулятор, который в зависимости от заданных типоразмеров шин, оборотов мотора и указанных передаточных чисел коробки рассчитает, какая будет скорость движения у автомобиля на передачи.
Конечно, калькулятор скорости автомобиля по передаточным числам и шинам производит расчет в идеальных (лабораторных) условиях. В реальных же условиях на конечную скорость автомобиля влияет очень много факторов, начиная от климатических условий и состояния дорожного полотна, и заканчивая настройкой мотора. Другими словами, калькулятор показывает потенциал коробки передач, до какой максимальной скорости она способна разогнать автомобиль.
Анализ методов определения скорости автомобиля при ДТП
По тормозному следу
Достоинства:
Недостатки:
По закону сохранения количества движения
Преимущества:
Недостатки:
Исходя из полученных демормаций
Преимущества:
Недостатки:
На практике чаще всего используют два метода – определение скорости по следу торможения и исходя из закона сохранения количества движения. При использовании двух этих методов одновременно обеспечивается максимально точный результат, так как методики дополняют друг друга.
Остальные способы определения скорости транспортного средства значительного распространения не получили по причине недостоверности получаемых результатов и/или необходимости громоздких и сложных вычислений. Также при оценке скорости автомобиля учитывают показания свидетелей происшествия, хотя в таком случае нужно помнить о субъективности восприятия скорости разными людьми.
В некоторой мере помочь разобраться с обстоятельствами происшествия и в итоге получить более точный результат может помочь анализ видео из камер наблюдения и видеорегистраторов.
Эмпирическая формула расчёта тормозного пути
Имея отличный водительский глазомер и достаточный опыт, каждый сможет определить расстояние до объекта на глаз, хотя бы примерно. Водительский опыт показывает, что для мгновенного вычисления длины тормозного пути по скорости, необходимо просто бросить взгляд на спидометр, оценить расстояние до препятствия, тогда тормозной путь будет равен половине числа, которое показывает спидометр. То есть, исходя из эмпирической формулы расчёта длины тормозного пути, безопасная дистанция до любого объекта будет равна мгновенной скорости, разделённой пополам. Практически так же производят расчёт скорости автомобиля по тормозному пути.
При этом нужно учитывать такое понятие, как остановочный путь, это термин экспертов дорожной полиции и он учитывает не только сам по себе тормозной путь, но и скорость реакции, а также время реагирования системы тормозов. В принципе — это расстояние до абсолютной остановки машины от того момента, когда водитель зафиксировал препятствие. Естественно, остановочный путь всегда больше тормозного, поскольку средняя скорость реакции здорового и трезвого водителя около 0,8 с, а тормозная система срабатывает ещё за 0,2-0,3 с. Следовательно, до полной остановки машины пройдёт ещё 1,1 с, а на скорости 60 км/ч автомобиль проходит 16,6 метров за одну секунду. Почти семнадцать метров, которые неминуемо будут добавляться к длине тормозного пути и которые редко учитываются большинством водителей. Вот именно поэтому необходимо серьёзно отнестись хотя бы к теоретическому вычислению длины тормозного пути.
Понятия и пояснения
Тормозной путь — это путь, который проходит автомобиль с момента, когда сработал тормозной механизм до полной остановки автомобиля. На него влияют:
Остановочный путь — путь с момента обнаружения опасности до полной остановки автомобиля. Понятно, что тормозной путь входит в остановочный. Кроме того в остановочный путь входят:
Первый параметр зависит от множества факторов, определяющим из которых является времени реакции водителя. По результатам многочисленных экспериментов, оно может меняться от 0,3 до 1,5 секунды. В среднем можно считать время реакции водителя равное 1 секунде. Кроме этого существует понятие «нормативное время восприятия сложной ситуации» равное 0,8 секунды. Также установлено, что время реакции у женщин, при возникновении сложной дорожной ситуации может достигать 2,5-3 секунд, тогда как у мужчин 1,5-2 секунды. Кроме этого на время реакции влияет:
Время срабатывания тормозной системы зависит от ее типа и технического состояния. Тормозная система с гидравлическим приводом срабатывает за 0,2 – 0,3 секунды, с пневматическим за 0,5 –0,6 секунд.
Время и путь реакции водителя
Время реакции водителя – это время, которое пройдет с момента обнаружения водителем опасности на дороге до начала принятия мер по ее предотвращению.
Путь реакции водителя – это путь, который пройдет автомобиль с момента обнаружения водителем опасности на дороге до нажатия педали тормоза.
Вот формула расчета пути, который пройдет автомобиль в момент реакции водителя на опасность:
(Скорость в км / ч: 10) x 3 = путь реакции в метрах
Пример расчета: представим, что вы едете со скоростью 100 км/ч по проселочной дороге и внезапно на дорогу выбегает лось. Расчет: (100 км/ч : 10) х 3 = 30 (метров). То есть, после того как вы среагируете на опасность на дороге, ваша машина проедет примерно 30 метров. Добавьте к этому тормозной путь автомобиля.
Внимание: эти правила не являются научно правильными формулами и дают только приблизительное значение!
Что нужно для расчёта тормозного пути
Чтобы вычислить тормозной путь формула которого указана на рисунке с пояснениями, мало знать моментальные сухие данные.
Теоретически, для оценки тормозных характеристик машины необходимо использовать массу данных:
Здесь нужно учитывать целый ряд моментов. К примеру, эффективность работы тормозной системы в каждом автомобиле может быть разной и это само собой разумеется. Гидравлическая система тормозов даёт задержку минимум 0,2-03 с, а пневматика, установленная на большинстве грузовиков и автобусов и того больше, до 0,6 с. Кроме этого, есть такое понятие, как нарастание тормозного усилия с нуля до максимального значения и это также отбирает от 0,4 до 0,6 с, при этом влияние скорости движения на длину тормозного пути в этом случае увеличивается в квадрате, то есть при увеличении скорости в два раза, тормозной путь будет вчетверо длиннее.
Расчет тормозного пути
Расчет тормозного пути машины при ее работе
В тормозных расчетах принимается во внимание общая тормозная сила машины, кН:
Критическими по отношению к возникновению юза являются режимы экстренного и автостопного торможения.
При возникновении юза, помимо возможного повреждения поверхностей катания колес (ползуны, выбоины) и повышения вероятности схода с рельсов, увеличивается тормозной путь, сцепление переходит в скольжение колеса по рельсу, т.к. коэффициент сцепления (в среднем 0,25) превышает коэффициент трения скольжения стали по стали (0,12 – 0,15).
Максимально допускаемое значение нажима колодки на колесо определяется с учетом коэффициента тормозного нажатия:
Коэффициент тормозного нажатия δ изменяется в широких пределах в зависимости от условий и типа подвижного состава δ=0,25–2,0. При чугунных тормозных колодках для самоходных путевых машин δ=0,5 – 0,6, а для несамоходных – δ=0,6 – 0,65; при композиционных тормозных колодках δ=0,3.
При взаимодействии поверхности башмака тормозной колодки и поверхности катания колеса происходит нагрев, вызывающий подплавление. При большой скорости движения возникает эффект, аналогичный наличию жидкой смазки.
Поэтому даже при постоянной силе K
нажима колодки, коэффициент трения φК и тормозная сила
B
Т изменяются с уменьшением скорости. Для стандартных чугунных колодок действующий коэффициент трения определяется по эмпирическим формулам:
– средняя скорость движения машины на расчетном интервале, м/с.

Расчет остановочного и тормозного пути автомобиля
Аналогично для композиционных колодок:
При расчетах тормозной путь путевых машин в приведенной массе подвижного состава рекомендуется учитывать инерционные свойства вращающихся масс колесных пар и приводов осевых редукторов:
где γ – коэффициент приведение (для самоходной машины γ=0,11 – 0,12, для несамоходной γ=0,03). Тогда из формулы второго закона Ньютона ускорение, м/с2:
С другой стороны, время, с, затрачиваемое на снижение скорости от начального значения V
Н до конечного значения
V
К, м/с2:
Считая на интервале времени движение равнозамедленным, действительный тормозной путь путевых машин (без учета пути, пройденного при подготовке тормозов) на рассматриваемом интервале снижения скоростей, м:
Общий действительный тормозной путь путевых машин на всем интервале снижения скорости определяется суммированием тормозных путей на составляющих интервалах деления с учетом изменения коэффициента трения башмаков колодок о поверхности катания колес.
Общий тормозной путь путевых машин рассчитывается как сумма действительного тормозного пути S
Д и пути
S
П, пройденного машиной при подготовке тормозов к срабатыванию. Путь, пройденный машиной при подготовке тормозов к срабатыванию:
– начальная скорость движения машины, м/с;
t
П – время на подготовку тормозов, с.

Билет 26. вопрос 19. уменьшение тормозного пути транспортного средства, не оборудованного антиблокировочной тормозной системой, достигается:
Подготовительное время на срабатывание тормозов для машины или хозяйственного поезда с числом осей менее 200:
С – приведенный уклон, принимаемый со знаком (+) на подъеме и со знаком (–) на спуске, о/оо;
b
Т – удельная тормозная сила, кН/т.
Удельная тормозная сила определяется по формуле:
В автостопном режиме время подготовки тормозов увеличивается на 12 с. Это время соответствует задержке срабатывания автостопа, необходимое для реакции машиниста на возникновение критических условий движения.
Также на эту тему Вы можете почитать
Планировщик балласта ПБ, устройство, технические характеристики
Развитие путевых машин, периоды развития путевых машин
СЗП-600. Самоходный землеуборочный поезд. Устройство и работа
Как увеличить интенсивность замедления
Из вышесказанного стало понятно, что называется тормозным путем и от чего зависит этот показатель. Однако возможно ли сократить расстояние, которое необходимо для остановки автомобиля? Возможно! Для этого существует два пути – поведенческий и технический. Идеально, если водитель сочетает оба способа.
Следует помнить, что сокращение времени, необходимого для остановки – один из способов обеспечения безопасности поездки. Поэтому каждый водитель должен постоянно следить за техническим состоянием своего «железного коня», своевременно обслуживать и ремонтировать систему торможения. Помимо этого, важно выбирать скорость движения с учетом окружающей обстановки: времени суток, состояния дороги, модели автомобиля и прочее.
Дополнительные составляющие тормозного пути
При вычислении эффективности тормозов очень большое значение имеет характеристика подвески и состояние шин. При чем тут подвеска? Очень просто. У нас под колёсами довольно редко встречается идеально ровный асфальт, а именно подвеска, точнее, амортизаторы, рессоры, торсионы и пружины как раз и прижимают колеса к поверхности, делая торможение и управление максимально эффективным. Если амортизатор неисправен, колеса подпрыгивают на ухабах и о полном контакте с покрытием не может быть и речи.
Давайте к этому прибавим кoэффициент сцепления резины с дорoгой — здесь огромное значение имеет состояние дороги, тип покрышки (зима или лето), рисунок протектора, геометрия, износ прoтектора и качество резиноматериала. Тесты показали, что на одном и том же автомобиле, но с разными покрышками, длина тормозного пути может изменяться до трёх-пяти метров, а о качестве пoкрытия и говорить нечего. Попробуйте сравнить тoрможение на сухом асфальте и на льду.
Как видим, факторов, влияющих на тормозной путь, а тем более на остановочный, достаточно много, поэтому предельная концентрация внимания за рулём — это гарантия безопасной езды. Проверяйте тормоза вовремя, не говорите по телефону за рулём и пусть все ваши дороги будут добрыми!
Условия торможения
Эффективность резкой остановки зависит от сопутствующих условий различного характера. Важно учитывать реакцию водителя, состояние тормозной системы авто и дорожного покрытия, а также погодные условия.
Чтобы корректно рассчитать тормозной путь (S), требуется использовать следующие данные:
Для этого используется такая формула:
На сцепление с дорогой напрямую влияет состояние дорожного покрытия. На сухой трассе машина будет останавливаться 20,25 метров, на мокрой дороге тормозное расстояние составит 35,4 метра, а на льду для полной остановки понадобится 70,8 метров. Соответственно, коэффициент сцепления при разных условиях будет отличаться.
На эффективность управления и остановки авто напрямую влияет способ торможения. Например, резкое нажатие на педаль тормоза может заклинить колеса и спровоцировать занос транспортного средства. Чтобы предотвратить такие ситуации, современные автомобильные производители используют систему ABS.
П О П У Л Я Р Н О Е:
PodR >Велосипед — хорошо, а с крышей да ещё и с мотором — это вообще круто! Лёгкий, удобный, экономичный и палаткой крытый сверху для защиты от дождя и ветра… много только положительного можно сказать об разработке от JMK-Innovation — PodRide.
Много похожих самоделок, как показано на фото изготавливается по всему миру и даже встречаются проекты мелкосерийного выпуска.
Для работы в сети Интернет нужна программа — браузер.
На компьютере пользоваться Интернет Вы можете стандартной Opera, а для своего телефона удобнее будет использовать Opera Mini.
Opera Mini — это один из популярных в мире браузеров, который отлично работает практически на любом телефоне. Подробнее…
Калькулятор остановочного пути автомобиля
Калькулятор определяет остановочный путь автомобиля с момента обнаружения водителем опасности до момента полной остановки автомобиля, а также другие параметры, связанные с этим событием, в частности, время восприятия водителем сигнала о необходимости торможения, время реакции водителя, а также расстояние, которое прошел автомобиль во время этих событий. Калькулятор также определяет начальную скорость (скорость до начала торможения) по известной длине торможения (длины тормозного пути) с учетом дорожных условий. Как и все остальные калькуляторы, этот калькулятор не следует использовать в судебных процессах и при необходимости получения высокой точности.
Рассчитать расстояние, необходимое для остановки автомобиля, движущегося со скоростью 90 км/ч по мокрой горизонтальной дороге с асфальтобетонным покрытием (коэффициент трения μ = 0,4) если время восприятия водителя 0,5 с и время реакции водителя 0,7 с.
Рассчитать начальную скорость автомобиля, движущегося по дороге с мокрым асфальтобетонным покрытием (μ = 0.4), если длина тормозного пути равна 100 м. Автомобиль движется на спуске с уклоном 10%.
Калькулятор остановочного пути
Калькулятор определения скорости по тормозному пути
Как рассчитать расстояние тормозного пути автомобиля.
Как быстро автомобиль ускоряется, наверное, знает большинство автовладельцев. Даже если вы не замеряли динамику разгона своей машины, вы наверняка смотрели заводские технические характеристики вашего авто, где обычно автопроизводитель указывает минимально возможное время разгона с 0-100 км/час. Но теперь вопрос: сколько времени нужно, чтобы остановить вашу машину? Вы знаете это? Уверены, что нет. Но, оказывается, рассчитать расстояние тормозного пути можно достаточно легко с помощью простой формулы. Мы расскажем вам, как это делается.
Определения и формулы
Остановочный путь
Остановочный путь — это расстояние, которое проходит автомобиль с момента, когда водитель видит опасность, оценивает ее, принимает решение остановиться и нажимает на педаль тормоза и до момента полной остановки автомобиля. Это расстояние является суммой нескольких расстояний, которые проходит автомобиль в то время, как водитель принимает решение, срабатывают механизмы тормозной системы и происходит замедление движения до полной остановки.
hr — расстояние, которое проедет автомобиль во время восприятия и оценки водителем ситуации,
s
hr — расстояние, которое проедет автомобиль во время во время реакции водителя на ситуацию,
s
brl — расстояние, которое проедет автомобиль во время задержки срабатывания тормозов, и
s
br — тормозной путь.
Расстояние, которое пройдет автомобиль во время восприятия и оценки водителем ситуации
Расстояние человеческого восприятия ситуации — это расстояние, которое пройдет автомобиль в то время, пока водитель оценивает опасность и принимает решение уменьшить скорость и остановиться. Оно определяется по формуле
hp расстояние человеческого восприятия в метрах,
v
скорость автомобиля в км/ч,
t
hp — время человеческого восприятия в секундах и 1000/3600 — коэффициент преобразования километров в час в метры в секунду (1 километр равен 1000 метров и 1 час равен 3600 секундам).
Расстояние, которое пройдет автомобиль во время реакции водителя
Расстояние реакции водителя — это расстояние, которое пройдет автомобиль пока водитель выполняет решение остановить автомобиль после оценки опасности и принятия решения об остановке. Оно определяется по формуле
hp — расстояние реакции водителя с метрах,
v
— скорость автомобиля в км/ч и
t
hr — время реакции водителя в секундах.
Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы
Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы, зависит от типа тормозной системы, установленной на автомобиле. Почти на всех легковых автомобилях и малотоннажных грузовых автомобилях используются гидравлическая тормозная система. На большинстве большегрузных автомобилей используются тормоза с пневматическим приводом. Задержка срабатывания пневматических тормозов приблизительно равна 0,4 с, а гидравлических (жидкость несжимаема!) 0,1–0,2 с. Общая задержка срабатывания тормозной системы измеряется как время от момента нажатия на педаль тормоза, в течение которого замедление становится устойчивым. Оно состоит из задержки срабатывания тормозной системы и времени установления постоянной величины замедления движения. В тормозной системе с пневматическим приводом воздуху необходимо время, чтобы пройти по тормозным магистралям. С другой стороны, в гидравлическом приводе задержек практически не наблюдается, и он работает в два—пять раз быстрее, чем пневматический.
Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы, определяется по формуле
brl — расстояние в метрах, которое пройдет автомобиль во время срабатывания тормозной системы,
v
— скорость движения автомобиля в км/ч,
t
brl — время срабатывания тормозной системы в секундах.
Замедление
Для упрощения расчетов предположим, что автомобиль движется с постоянным ускорением или замедлением, которое определяется по известной из курса элементарной физики формуле равноускоренного или равнозамедленного движения
— ускорение,
v
— начальная скорость,
v
— конечная скорость и
t
— время.
Тормозной путь автомобиля
Тормозной путь автомобиля — это расстояние, которое проходит автомобиль с момента полного нажатия на педаль тормоза до момента полной остановки. Это расстояние зависит от скорости автомобиля перед началом торможения и от коэффициента трения между шинами и дорожным покрытием. В этом калькуляторе мы не учитываем другие факторы, влияющие на тормозной путь, например, сопротивление качению шин или лобовое сопротивление воздуха
Вывод зависимости тормозного пути от скорости и трения с использованием второго закона Ньютона
Коэффициент трения определяется как отношения силы трения к силе нормального давления, прижимающей тело к опоре:
Бесплатная программа для расчёта скорости и тормозного пути
Как определить скорость автомобиля и тормозной путь?
Ниже рассматривается небольшая бесплатная программка для расчёта тормозного пути автомобиля при известной скорости и наоборот (можно рассчитать скорость при известном тормозном пути).
Тормозной путь — это расстояние, проходимое транспортным средством от момента привода в действие тормозного устройства до полной остановки.
Полный тормозной путь включает в себя также расстояние, проходимое за время от момента восприятия водителем (машинистом) необходимости торможения до приведения в действие органов управления тормозами.
Длина тормозного пути пропорциональна квадрату скорости движения, быстроте срабатывания тормозов, нагрузке, приходящейся на затормаживаемые колёса, коэффициенту сцепления колёс с дорогой, а также зависит от реакции водителя. Длина тормозного пути зависит от состояния тормозной системы, скорости движения автомобиля, состояния дороги, а также от состояния и качества шин. При увеличении скорости движения автомобиля, например в 2 раза, тормозной путь возрастает примерно в 4 раза. На мокрой дороге тормозной путь легкового автомобиля увеличивается по сравнению с сухой дорогой в 2 раза, а на заснеженной и обледеневшей поверхности дороги – примерно в 4 раза. Остановочный путь включает тормозной путь, а также расстояние, которое проходит автомобиль за время реакции водителя (от осознания опасности до начала нажатия на педаль тормоза). Отрезок пути, который проходит автомобиль за время реакции водителя, автомобиль движется с неизменной скоростью.
Как определить скорость автомобиля по тормозному пути?
Равнозамедленное движение: v х v/2=Sa,
где v — скорость до начала торможения,
S-пройденный путь (длина черного следа резины размазанной по асфальту),
a-ускорение (замедление) в торможении.
Это берется из перехода ВСЕЙ кинетической энергии в работу силы трения (разрушение резины, т.е. черный след). Значение коэффициента сцепления может быть от 0.7-0.9 для сухого асфальта и хорошей резины до 0.03-0.01 на льду. Умелое торможение на грани блокировки колес (работа хорошей АБС) могут повысить коэффициент трения процентов на 10-20, но это не наш случай: раз черный след на асфальте — колеса были заблокированы. Минимально допустимая эффективность тормозов для легковушки 0.64 (на каждую тонну веса тормозное усилие 640 кг) регламентируется в ГОСТ 25478-91 для вообще тормозов. Предполагается что на сухом асфальте (или на резине барабана на ПИК) сцепление резины гораздо лучше, так что это качество собственно тормозов. В остановочный путь еще входит расстояние пройденное с начальной скоростью за время реакции водителя (0.2 сек) и время срабатывания тормозной системы (по ГОСТ 25478-91 не хуже 0.5 сек для легковушек). Черного следа на асфальте в это время не остается, и в расчетах скорости из длины тормозного следа поэтому используют только тормозной путь.
Скорость по тормозному пути, зафиксированному в протоколе, будут определять в ГИБДД: у них имеется рукописная схема, где напротив определенной длины тормозного пути выставлена соответствующая скорость; плюс-минус для них дело несущественное.
Расчет тормозного пути и скорости
Экспертиза ГИБДД и МВД использует следующие формулы и методики. Можете сами найти и сделать расчеты.
Va =0.5 х t3 х j + v2Sю х j = 0,5 0,3 5 + v2 х 21 х 5 = 0,75 +14,49 = 15,24м/с =54,9 км/ч
где: в выражении v2Sю х j, v — это квадратный корень для всего выражения, просто не получилось при написании. Va — начальная скорость автомобиля, м/с; t3 — время нарастания замедления автомобиля, с; j — установившееся замедление автомобиля при торможении, м/с2; (для мокрого покрытия-5м/с2 по ГОСТ 25478-91 или приложению ниже) для сухого покрытия j=6,8 м/с2, отсюда начальная скорость автомобиля при «юзе» в 21м равна 17,92м/с, или 64,5км/ч; Sю — длинна тормозного следа (юза), м.
T0 = t1 + t2 + t3 + t4 = T + Va / j; приняв Т = t1 + t2 + 0,5 t3 можно легко расчитать остановочный путь и остановочное время автомобиля. Это можно расчитать для сравнения условий движения двух участников ДТП.
Тормозной путь S=Kэ*V*V/(254*Фc), где Кэ-тормозной коэффициент (для легкового автомобиля =1); V — скорость в км/ч в начале торможения; Фc — коэффициент сцепления с дорогой (=0.7 сухой асфальт, 0.4 мокрая дорога, 0.2 укатанный снег, 0.1 обледенелая дорога).
След юза
В экспертной практике принято считать, что следы юза, вызванные блокировкой колес, остаются только в период полного торможениия (т.е. торможение в пол), а момент начала следообразования совпадает с моментом возникновения установившегося замедления, отсюда: Sю=Vю*Vю/2j, где Sю — длина следа торможения (м); Vю — скорость автомобиля в начале полного торможения (м/с) j — установившееся замедление транспортного средства при полном использовании сцепления всеми шинами автомобиля (м/(с*с))
Источник