АННОТАЦИЯ
Актуальность и цель. Объект исследования – ременная передача, состоящая из двух шкивов и ремня. Предмет исследования – тяговые характеристики ремня. Тяговая способность ремня и ременной передачи характеризуется экспериментальными графиками зависимостей относительного скольжения ремня и коэффициента полезного действия от коэффициента тяги передачи. Задача состоит в разработке математической модели ременной передачи, позволяющей теоретически оценивать тяговую способность ремня и рациональный режим работы в зоне упругого скольжения.
Материалы и методы. Кинематический и силовой расчет ременной передачи построен на теории упругого скольжения ремня по шкивам, разработанной Н. П. Петровым и Н. Е. Жуковским. В соответствии с этой теорией на шкивах существуют дуги упругого скольжения ремня. При этом вследствие упругого скольжения отношение скоростей точек ведомой и ведущей ветвей ремня линейно связано с относительным скольжением ремня, равным разности относительных удлинений ветвей. В статье предложена математическая модель ременной передачи, в основу которой положены новое полученное уравнение связи между скоростями точек ведущей и ведомой ветвей ремня и уравнения движения ремня как сплошной среды.
Результаты. Разработана математическая модель ременной передачи, позволяющая изучать тяговые характеристики ремня и определять рациональный режим работы. Разработана компьютерная модель, с помощью которой получены оценки тяговых характеристик.
Новизна. Предложено новое уравнение связи между скоростями точек ведущей и ведомой ветвей ремня.
Выводы. В режиме отсутствия буксования ремня эффективность ременной передачи возрастает при уменьшении коэффициента запаса сцепления. Коэффициент полезного действия достигает максимума при такой нагрузке, когда коэффициент запаса сцепления на одном из шкивов уменьшается до минимально допустимого. Чтобы поддерживать заданный коэффициент запаса сцепления, при изменении нагрузки силу натяжения ремня целесообразно регулировать.
ABSTRACT
Background. The object of research is belt transmission that consists of two pulleys and a belt. Subject of research is the traction characteristics of a belt. The challenge is to develop a mathematical model of the belt transmission, allowing in theory to evaluate the traction capacity of a belt and a rational mode of operation.
Materials and methods. Mathematical model of belt transmission is based on equation relationship between the velocities of lead and driven belt branches points and the equations of motion of the belt.
Results. The developed mathematical model of the belt transmission allows to study the belt traction characteristics and to determine a rational mode of operation. It was developed the computer model to estimate the traction experimental characteristics.
The novelty. It is proposed the new equation relationship between the speeds of points of leading and driven belt branches.
Conclusions. Belt transmission efficiency increases with decreasing safety factor of adhesion. Coefficient of efficiency reaches its maximum at this load, when the factor of adhesion on one of the pulleys is reduced to the minimum. To maintain the specified factor of adhesion, when changing the load force it is advisable to adjust the belt tension.
Введение
Кинематический и силовой расчет ременной передачи построен на теории упругого скольжения ремня по шкивам, разработанной Н. П. Петровым и Н. Е. Жуковским [2]. В соответствии с этой теорией на шкивах существуют дуги упругого скольжения ремня. При этом вследствие упругого скольжения отношение скоростей точек ведомой и ведущей ветвей ремня линейно связано с относительным скольжением ремня, равным разности относительных удлинений ветвей.
Статья посвящена разработке математической модели ременной передачи, в основу которой положены новое полученное уравнение связи между скоростями точек ведущей и ведомой ветвей ремня и уравнения движения ремня как сплошной среды.
1. Объект исследования и основные обозначения
Ременная передача – это механическая система, состоящая из ведущего шкива, ведомого шкива и соединяющего их ремня.
Введем следующие обозначения (рис. 1):
R1, R2 – радиус шкива 1 и шкива 2 соответственно, м;
L – расстояние между осями шкивов 1 и 2, м;
/Belov1%20.files/image001.png) s – площадь поперечного сечения плоского ремня, м2;
s – площадь поперечного сечения плоского ремня, м2;
δ – половина толщины ремня, м;
α1, α2 – радиальный угол охвата ремнем ведущего и ведомого шкива, рад;
r1, r2 – радиус цапфы вала ведущего и ведомого шкива, м;
![]() ,
, ![]() – относительное удлинение cрединного волокна ведущей и ведомой ветви ремня соответственно;
– относительное удлинение cрединного волокна ведущей и ведомой ветви ремня соответственно;
![]() 1,
1, ![]() 2 – угловая скорость шкива 1 и шкива 2 соответственно, рад/с;
2 – угловая скорость шкива 1 и шкива 2 соответственно, рад/с;
![]() ,
, ![]() – скорость набегающей на шкив точки ремня ведущей и ведомой ветви соответственно, м/с;
– скорость набегающей на шкив точки ремня ведущей и ведомой ветви соответственно, м/с;
u – передаточное отношение;
ρ – плотность ремня, кг/м3;
![]() ,
, ![]() – величина силы натяжения ведущей и ведомой ветви ремня соответственно без учета веса, Н;
– величина силы натяжения ведущей и ведомой ветви ремня соответственно без учета веса, Н;
![]() – начальная сила натяжения ремня без учета веса, Н;
– начальная сила натяжения ремня без учета веса, Н;
E – модуль упругости ремня, Па;
![]() – начальное нормальное напряжение в сечении ремня, Н;
– начальное нормальное напряжение в сечении ремня, Н;
![]() – предел упругости ремня, Па;
– предел упругости ремня, Па;
f – коэффициент трения скольжения ремня со шкивом;
µ – коэффициент трения скольжения во вращательной паре “вал шкива − опора”;
M1, M2 – величина момента пары сил, приводящих в движение ведущий шкив 1, и пары сил полезного сопротивления (рабочей нагрузки), действующих на ведомый шкив 2 соответственно, Н м;
![]() ,
, ![]() – величина момента силы трения во вращательной паре “вал − опора” ведущего и ведомого шкива относительно оси вращения соответствующего шкива, Н м;
– величина момента силы трения во вращательной паре “вал − опора” ведущего и ведомого шкива относительно оси вращения соответствующего шкива, Н м;
P1, P2 – мощность момента M1, M2 пары сил соответственно, Вт;
η – коэффициент полезного действия ременной передачи.
2. Формулировка задачи
Тяговая способность ремня и ременной передачи характеризуется экспериментальными графиками зависимостей относительного скольжения ремня и коэффициента полезного действия от коэффициента тяги передачи [2, с. 137, 138]. Задача состоит в разработке математической модели ременной передачи, позволяющей теоретически оценивать тяговую способность ремня и рациональный режим работы в зоне упругого скольжения.
3. Кинематика ременной передачи
Рассмотрим ременную передачу с ведущим шкивом 1 и ведомым 2 при неизменной нагрузке и равномерных вращениях шкивов. В соответствии с исследованиями Н. П. Петрова и Н. Е. Жуковского дуга охвата шкива ремнем состоит из участков сцепления и скольжения [2, с. 130]. /Belov1%20.files/image014.png) Пусть точки A, C и K, E– концевые точки дуги охвата ремнем ведущего и ведомого шкива соответственно (рис. 2). На участках AB и KD набегания ремня на ведущий и ведомый шкив ремень не скользит по шкиву. Следовательно, скорость
Пусть точки A, C и K, E– концевые точки дуги охвата ремнем ведущего и ведомого шкива соответственно (рис. 2). На участках AB и KD набегания ремня на ведущий и ведомый шкив ремень не скользит по шкиву. Следовательно, скорость ![]() точек участка AB ведущей ветви ремня равна скорости точки A равномерно вращающегося шкива. При этом скорости точек участка BC ремня, касающегося ведущего шкива, уменьшаются до
точек участка AB ведущей ветви ремня равна скорости точки A равномерно вращающегося шкива. При этом скорости точек участка BC ремня, касающегося ведущего шкива, уменьшаются до ![]() в точке С схода, то есть участок BC ремня «отстает» от шкива из-за укорочения и скользит по нему. Аналогичные условия должны соблюдаться на дуге KE ведомого шкива. Скорость
в точке С схода, то есть участок BC ремня «отстает» от шкива из-за укорочения и скользит по нему. Аналогичные условия должны соблюдаться на дуге KE ведомого шкива. Скорость ![]() точки K ведомой ветви ремня при набегании на шкив равна скорости точки K шкива. При этом скорости точек участка DE ремня, касающихся шкива, увеличиваются до
точки K ведомой ветви ремня при набегании на шкив равна скорости точки K шкива. При этом скорости точек участка DE ремня, касающихся шкива, увеличиваются до ![]() в точке E схода, то есть участок DE ремня «опережает» шкив из-за удлинения:
в точке E схода, то есть участок DE ремня «опережает» шкив из-за удлинения:
/Belov1%20.files/image015.png) (1)
(1)
При буксовании ремня равенства (1) не соблюдаются.
Рассмотрим участок AC ремня, огибающий ведущий шкив. За время t его место займет участок AA1 длиной ![]() ведущей ветви, а участок AC займет положение CС1 длиной
ведущей ветви, а участок AC займет положение CС1 длиной ![]() ведомой ветви:
ведомой ветви:
![]() ; .
; .![]() . (2)
. (2)
Участки AA1 и CС1 в разные моменты времени представляют один и тот же участок AC ремня и имеют длину ![]() в недеформированном состоянии. Следовательно,
в недеформированном состоянии. Следовательно,
![]() ;
; ![]() . (3)
. (3)
Подставляя выражения для ![]() ,
, ![]() из равенств (3) в равенства (2) и исключая время t, придем к такому равенству:
из равенств (3) в равенства (2) и исключая время t, придем к такому равенству:
![]() . (4)
. (4)
По определению,
![]()
или с учетом равенств (1), (4)
![]() . (5)
. (5)
Формула (5) справедлива при отсутствии буксования ремня. Она доказывает, что передаточное отношение ременной передачи равно отношению радиусов ведомого и ведущего шкивов, умноженному на коэффициент пропорциональности, который не равен единице и зависит от относительных удлинений ведущей и ведомой ветвей ремня.
4. Динамика шкива и ремня
Установим соотношения между величинами моментов M1, M2 . Вес ремня учитывать не будем. Можно доказать, что он не влияет на работу движущих сил. Примем, что при неизменной нагрузке 1) вращения шкивов равномерные; 2) движение ремня установившееся; 3) ремень находится в упругом состоянии растяжения.
/Belov1%20.files/image026.png) Выделим часть ремня, охватывающую ведущий шкив, как сплошную среду (рис. 3). Среда ограничена контрольной поверхностью, состоящей из цилиндрических внутренних и внешних поверхностей, двух боковых поверхностей, перпендикулярных оси вращения шкивов, и двух плоских радиальных поперечных сечений набегания и схода ремня. На контрольной поверхности действуют следующие силы: 1) равнодействующие
Выделим часть ремня, охватывающую ведущий шкив, как сплошную среду (рис. 3). Среда ограничена контрольной поверхностью, состоящей из цилиндрических внутренних и внешних поверхностей, двух боковых поверхностей, перпендикулярных оси вращения шкивов, и двух плоских радиальных поперечных сечений набегания и схода ремня. На контрольной поверхности действуют следующие силы: 1) равнодействующие ![]() ,
, ![]() сил натяжения ведущей и ведомой ветви соответственно; 2) равнодействующая
сил натяжения ведущей и ведомой ветви соответственно; 2) равнодействующая ![]() реакций ведущего шкива.
реакций ведущего шкива.
При неизменном сопротивлении движение ремня как сплошной среды – установившееся. Полагая, что плотности и площади поперечного сечения ведомой ветви и ремня в ненапряженном состоянии отличается незначительно, запишем уравнение сохранения масс в интегральном виде [3, с. 54]:
![]() ,
,
где ![]() ,
, ![]() − плотности и площадь поперечного сечения ведущей ветви ремня.
− плотности и площадь поперечного сечения ведущей ветви ремня.
Момент силы или количества движения материальной точки относительно оси шкива будем считать положительным, если при взгляде на рисунок сила или количество движения стремятся вращать шкив вокруг оси против хода стрелки часов. Уравнение моментов количества движения относительно оси O вращения шкива ремня на шкиве при установившемся движении запишем в интегральном виде [3, с. 54]:
![]()
или с учетом уравнения сохранения масс
![]() , (6)
, (6)
где ![]() – величина момента силы
– величина момента силы ![]() относительно оси шкива.
относительно оси шкива.
Уравнение равномерного вращения шкива 1 представим в виде уравнения равновесия моментов сил относительно оси вращения:
![]() .
.
Следовательно, уравнение (6) можно записать так:
![]()
или
![]() . (7)
. (7)
Рассматривая участок ремня, охватывающий ведомый шкив, придем к аналогичному уравнению:
![]() . (8)
. (8)
При неизменности общей длины ремня растяжение ведущей ветви «компенсируется» сжатием ведомой ветви, то есть уменьшение силы сжатия «компенсируется» увеличением силы растяжения:
![]() (9)
(9)
или
![]() . (10)
. (10)
Найдем величины ![]() ,
, ![]() моментов сил трения во вращательной паре ведущего и ведомого шкива. На ведущий шкив со стороны элемента ab ремня действует элементарная нормальная сила dN1 и элементарная сила dT1 трения сцепления, а на ведомый шкив – соответственно dN2 и dT2. На вал ведущего шкива со стороны опоры действует элементарная сила, уравновешивающая силу dN1 и элементарная сила dQ1 трения, а на вал ведомого шкива − силы dN2, dQ2 (рис. 4).
моментов сил трения во вращательной паре ведущего и ведомого шкива. На ведущий шкив со стороны элемента ab ремня действует элементарная нормальная сила dN1 и элементарная сила dT1 трения сцепления, а на ведомый шкив – соответственно dN2 и dT2. На вал ведущего шкива со стороны опоры действует элементарная сила, уравновешивающая силу dN1 и элементарная сила dQ1 трения, а на вал ведомого шкива − силы dN2, dQ2 (рис. 4).
По определению,
/Belov1%20.files/image042.png) (11)
(11)
Силы трения скольжения связаны с силами давления такими равенствами:
![]() ;
; ![]() .
.
Следовательно, формулы (11) можно переписать так:
/Belov1%20.files/image045.png) (12)
(12)
/Belov1%20.files/image046.png) Установим связь между силами растяжения ремня и силами давления ремня на шкив.
Установим связь между силами растяжения ремня и силами давления ремня на шкив.
/Belov1%20.files/image047.png) Рассмотрим элемент ab ремня на ведущем шкиве с элементарным радиальным углом dα (рис. 5). На него действуют силы растяжения
Рассмотрим элемент ab ремня на ведущем шкиве с элементарным радиальным углом dα (рис. 5). На него действуют силы растяжения ![]() и
и ![]() , вес, нормальная и касательная составляющие реакции шкива, элементарные равнодействующие которых равны dN и dT. Приращение
, вес, нормальная и касательная составляющие реакции шкива, элементарные равнодействующие которых равны dN и dT. Приращение ![]() вектора
вектора ![]() имеет проекцию
имеет проекцию ![]() на ось касательной к окружности шкива и проекцию
на ось касательной к окружности шкива и проекцию ![]() на ось нормали к окружности шкива:
на ось нормали к окружности шкива:
/Belov1%20.files/image053.png)
Расчеты показали, что касательное ускорение точек ремня, обусловленное его деформацией, приводит к изменению сил натяжения ремня менее чем на 1% и им можно пренебречь. Вес ремня не влияет на работу движущих сил, и его также не будем учитывать. Рассмотрим предельный случай, когда скорость точки элемента ремня наибольшая и давление ремня на шкив наименьшее. Уравнения движения центра масс элемента ab ремня массы ![]() на ведущем шкиве в естественном виде [1] запишем так:
на ведущем шкиве в естественном виде [1] запишем так:
/Belov1%20.files/image055.png)
Проинтегрируем обе части уравнений по всем элементам ab ремня на дуге охвата ремня по окружности шкива 1:
/Belov1%20.files/image056.png) (13)
(13)
Формулы (12) с учетом равенств (9), а также (13) и аналогичных для ведомого шкива примут такой вид:
/Belov1%20.files/image057.png) (14)
(14)
По определению, условие отсутствия буксования ремня на ведущем шкиве можно записать так:
![]()
или с учетом равенств (13)
![]() (15)
(15)
Условие отсутствия буксования для ведомого шкива выводится аналогично:
![]() (16)
(16)
Сцепление ремня с ведущим и ведомым шкивом характеризуется соответственно коэффициентом β1, β2 запаса сцепления:
/Belov1%20.files/image061.png) (17)
(17)
Уравнения (4), (7), (8), (10) позволяют найти четыре неизвестные ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Они справедливы при отсутствии буксования ремня.
. Они справедливы при отсутствии буксования ремня.
Отметим, что искомые неизвестные являются константами, если момент пары сил нагрузки не изменяется. Если момент пары сил изменяется и задан как функция времени, то при малом моменте сил инерции шкивов четыре неизвестные ![]() ,
, ![]() ,
, ![]() ,
, ![]() определяются из тех же уравнений как функции от времени.
определяются из тех же уравнений как функции от времени.
5. Алгоритм расчета
1. Задаем исходные данные: R1 [м]; R2 [м]; L [м]; r1 [м]; r2 [м]; s [м2]; ρ [кг/м3]; ![]() 1 [рад/с]; M2 [Н м];
1 [рад/с]; M2 [Н м]; ![]() [Па]; E [Па];
[Па]; E [Па]; ![]() [Па]; f ; µ.
[Па]; f ; µ.
2. Определяем углы охвата ремней, скорость точки ведущей ветви по формуле (1), начальной силы растяжения ремня и моментов холостого хода по формулам (14).
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
3. Отмечаем, что три уравнения (4), (8), (10) содержат три неизвестные ![]() ,
, ![]() ,
, ![]() . Они приводятся к кубичному уравнению относительно переменной z:
. Они приводятся к кубичному уравнению относительно переменной z:
![]() ,
,
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
4. Находим единственный корень z кубического уравнения на отрезке [0, 1] численным методом (например, методом Ньютона) и определяем скорость точки ведомой ветви ремня: ![]() .
.
5. Определяем неизвестные ![]() ,
, ![]() из уравнений (4), (10):
из уравнений (4), (10):
![]() ;
; ![]() ;
;
6. Определяем силы натяжения и момент пары движущих сил из уравнений (7): ![]() , Н;
, Н; ![]() , Н;
, Н;
![]() , Н м.
, Н м.
7. Проверяем условия (15), (16) отсутствия буксования:
![]() ;
; ![]()
8. Проверяем условие упругости ремня по среднему слою: ![]() .
.
9. При выполнении условий в п. 7, 8 определяем угловую скорость ведомого шкива по формуле (1): ![]() , рад/с.
, рад/с.
10. Определяем передаточное отношение по формуле ![]() .
.
11. Определяем мощности движущих сил и сил сопротивления:
![]() ;
; ![]() .
.
12. Оцениваем коэффициент полезного действия ременной передачи:
![]() .
.
13. Оцениваем относительное скольжение ![]() ремня по формуле
ремня по формуле
![]() .
.
14. Оцениваем коэффициент ![]() тяги передачи по формуле
тяги передачи по формуле ![]() .
.
15. Оцениваем коэффициенты запаса сцепления по формулам (17).
6. Анализ тяговых характеристик
Рассчитаем тяговые характеристики ременной передачи (табл. 1).
1. Исходные данные
|
R1, м |
R2, м |
L, м |
r1, мм |
r2, мм |
s, мм2 |
δ, мм |
ρ, кг/м3 |
|
M2, Н м |
|
E, МПа |
|
f |
µ |
|
0,1 |
0,2 |
0,7 |
10 |
20 |
160 |
2 |
1200 |
800 |
40 |
1,6 |
160 |
2,2 |
0,3 |
0,12 |
Расчет произведем по формулам алгоритма, полагая, что единицы измерения исходных данных приведены к системе СИ.
/Belov1%20.files/image099.png) Сила растяжения и относительное удлинение ведущей ветви ремня увеличиваются, а ведомой − уменьшаются с увеличением момента пары сил нагрузки (рис. 6). При этом коэффициент
Сила растяжения и относительное удлинение ведущей ветви ремня увеличиваются, а ведомой − уменьшаются с увеличением момента пары сил нагрузки (рис. 6). При этом коэффициент ![]() тяги и относительное скольжение возрастают (рис. 7, слева).
тяги и относительное скольжение возрастают (рис. 7, слева).
Коэффициент полезного действия передачи увеличивается с увеличением момента пары сил нагрузки от 5 до 40 Н м и увеличении коэффициента тяги (рис. 7, справа).
/Belov1%20.files/image100.png)
С увеличением нагрузки коэффициент β1 запаса сцепления ремня с ведущим шкивом и β2 с ведомым шкивом уменьшаются (рис. 8, слева).
/Belov1%20.files/image101.png) |
При уменьшении коэффициента запаса сцепления на одном из шкивов до 1 эффективность ременной передачи возрастает. Коэффициент полезного действия достигает максимума при такой нагрузке и тяге, когда коэффициент запаса сцепления на одном из шкивов уменьшится до минимально допустимого.
Чтобы поддерживать заданный коэффициент запаса сцепления, при повышении нагрузки силу натяжения ремня необходимо регулировать, увеличивая ее прямо пропорционально моменту пары сил нагрузки (рис. 8, справа).
Рассмотрим вариант модели, когда в исходных данных вместо начальной силы натяжения ремня или начального нормального напряжения ![]() в сечении ремня задано значение β коэффициента запаса сцепления
в сечении ремня задано значение β коэффициента запаса сцепления ![]() .Тогда равенство (10) с учетом (17) можно переписать так:
.Тогда равенство (10) с учетом (17) можно переписать так:
![]() , (18)
, (18)
где /Belov1%20.files/image104.png)
Уравнения (4), (7), (8), (18) позволяют найти четыре неизвестные ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Начальная сила натяжения ремня определяется по формуле (10):
. Начальная сила натяжения ремня определяется по формуле (10):
![]() .
.
Как показали расчеты, если коэффициент запаса сцепления на одном из шкивов равен 1, то есть дуги упругого скольжения и охвата шкива ремнем совпадают, то справедлива формула Эйлера без учета «вклада» сил инерции, деформации и толщины ремня: ![]() .
.
Снижение модуля упругости ремня в процессе эксплуатации приводит к ухудшению характеристик передачи (рис. 9).
/Belov1%20.files/image107.png) |
При снижение эксплуатационных характеристик ремня дополнительное растяжение позволяет уменьшить коэффициент запаса сцепления и увеличить коэффициент полезного действия передачи.
Выводы
1. Компьютерная модель ременной передачи позволяет оценить тяговые характеристики ремня.
2. В режиме отсутствия буксования ремня эффективность ременной передачи возрастает при уменьшении коэффициента запаса сцепления. Коэффициент полезного действия достигает максимума при такой нагрузке, когда коэффициент запаса сцепления на одном из шкивов уменьшится до минимально допустимого.
3. Чтобы поддерживать заданный коэффициент запаса сцепления, при изменении нагрузки силу натяжения ремня целесообразно регулировать.
Список литературы:
1. Белов.М.И. , Пылаев Б.В. Теоретическая механика. 2-е изд., перераб. и доп. − М.: ИНФРА-М, 2016. − 336 с. / [Электронный ресурс]. – Ре-жим доступа: URL: http://znanium.com/catalog.php?bookinfo=556474 (дата обращения 12.05.2017).
2. Гузенков П. Г. Детали машин. − М.: Высшая школа, 1982. − 352 c
3. Седов Л. И. Механика сплошной среды. том II. Учебник. − М.: Наука, 1976. − 574 с.
Диаметры шкивов и скорость ремня
Диаметры шкивов определяются в зависимости
от типа передачи, передаваемой мощности
и передаточного отношения. Расчет
передачи выполняется по диаметру малого
шкива D1,
минимальное значение которого для
клиновых ременных передач представлено
в табл. П36, для поликлиновых – в табл.
П38. Диаметры шкивов клиноременной и
поликлиновой передачи по ГОСТ 50641-94
(соответствуют ряду чиселRа40,
с предпочтением по рядуRа20):
63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 224, 250, 280,
315, 355, 400, 450, 500, 560, 630, 710, 800, 900, 1000 и т.д.
При выборе диаметров из числа стандартных
следует учитывать, что при меньших
диаметрах уменьшаются габариты передачи,
но увеличивается число ремней.
Диаметры делительных окружностей
зубчатых шкивов определяют по формуле
D = mz.
При этом окружная скорость ремня на
ведущем шкиве, м/с: v1= πD1n1/60000;
на ведомом –v2= πD2n2/60000.
Скоростиv1 и
v2не должны
быть меньше допустимых значений, табл.
2.39, табл. П36, табл. П38, табл. П49.
Угол обхвата
Дуга обода шкива, на которой он
соприкасается с ремнем, называется
дугой обхвата, а соответствующий ей
центральный угол называется углом
обхвата α (рис. 2.39). Угол обхвата ремнем
меньшего шкива определяется по выражению:
α = 180º – 57º(D2–D1)/a,
град.
По углу обхвата вычисляется угол между
ветвями ремня (рис. 2.39), град:
γ = 180º – α.
Для зубчатых ремней по углу α определяют
число зубьев в зацеплении на малом
шкиве:
z0=z1/ 360º.
Межосевое расстояние и расчетная длина ремня
Межосевое расстояние аопределяется
в основном конструкцией привода.
Например, межцентровое расстояние
передачи 160/200, изображенной на рис. 2.41,
будет определяться как сумма межосевых
расстояний междуI,IIвалами иII,IIIвалами.
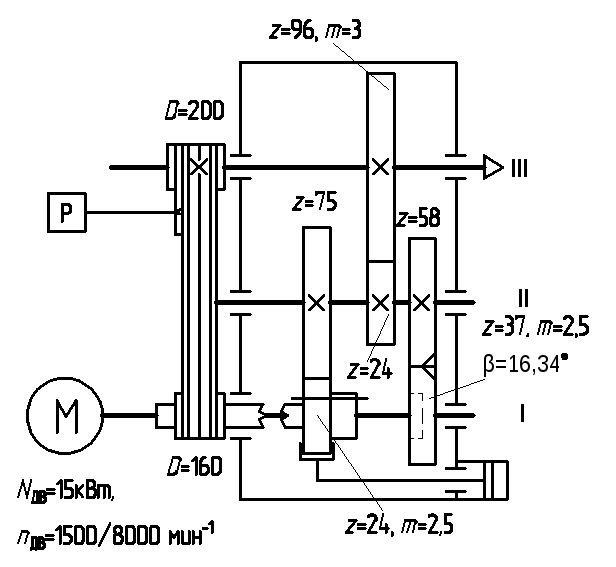
Рис. 2.41.
Кинематическая схема привода со сложенной
структурой
Минимальные значения а зависят от
типа передачи и диаметров шкивов.
Рекомендуемоеадля клиноременных
и зубчатых передач по ГОСТ 1284.3-96:
0,7 (D1+D2)a2 (D1+D2).
Для поликлиновых передач аограничивают
углом обхвата1500.
После определения межцентрового
расстояния a, находится
расчетная длина ремняLp,
мм:
Lр= 2a+π(D1+D2)/2 + (D2–D1)2/(4a).
Длина ремней отечественного производства
стандартизована. Для нормальных сечений
Lвыбирается по рядуRa40, для узких и
поликлиновых ремней – по рядуRa20.
Для ремней импортного производства
длина ремня приведена в табл. 2.41, табл.
2.44.
При заданной длине ремня межосевое
расстояние aпересчитывается:
![]() .
.
При этом расположение валов в редукторе
может поменяться (рис. 2.16).
Для зубчатых ремней по расчетной длине
ремня определяется расчетное число
зубьев ремня zр:
zр=Lp/(πm).
Полученное значение zрокругляется до ближайшего целого по
табл. П39. После этого устанавливается
окончательная длина зубчатого ремня,
мм:
L=πmzр.
2.9.5. Методика расчета ременных передач по тяговой способности
Основными критериями расчета ременных
передач являются тяговая способность
или прочность сцепления ремня со шкивом
и долговечность ремня. Ограниченное
число типоразмеров стандартных клиновых
ремней позволило определить допускаемую
нагрузку для каждого типоразмера ремня,
а расчет передачи свести к подбору типа
и числа ремней по методике, изложенной
в ГОСТ 1284.3-80.
Соседние файлы в папке Устинов
- #
- #
- #
- #
- #
В этой статье
- История
- Устройство ременной передачи
- Открытая, перекрестная и полуперекрестная передача
- Повышающая и понижающая передача
- Как посчитать передаточное отношение для ремённой передачи
- Передаточное число
- Передаточное отношение многоступенчатой ремённой передачи
- Виды приводных ремней
- Преимущества и недостатки ремённых передач
- Определения
- Вопросы
- Задачи
- Полезное видео
История
Ремённая передача – одна из древнейших и простых механических передач, в которой используются приводные ремни и специальные колеса — шкивы. По некоторым источникам, ременная передача впервые документально описана китайским философом, поэтом и политиком Ян Сюном (53 год до н. э. – 18 год н. э.) периода империи Хань в тексте «Словарь местных выражений». Описанное устройство использовали ткачи в своей работе с шелком.
Кстати, слово «ремённая» записывается через букву «ё», на которую и нужно ставить ударение. Но в печати, например, в нашем следующем заголовке, точки над «ё» могут опускать. Это не является ошибкой, но не забудьте ставить ударение правильно.
На средневековых картинах можно увидеть механизм — самопрялку, в которой принцип ремённой передачи используется для ускорения получения пряжи. Большое развитие ремённая передача вместе с другими механизмами получила во времена английской промышленной революции (1780-1830 гг.), которая началась с изобретения в 1769 году паровой машины. Небольшие кустарные ремесленные производства начали вытесняться фабричным трудом с большим количеством машин.


На приведенной ниже картинке показаны примеры использования ремённой передачи в современных технических устройствах – от двигателя внутреннего сгорания автомобиля до 3D-принтера.

Устройство ременной передачи
Ведущее и ведомое колесо – это шкивы. Их соединяет приводной ремень. Ведущий шкив — тот, который крутит мотор или другая внешняя сила, а ведомый – следующий за ним. Часто для предотвращения соскакивания ремня на ободе шкива делают канавку или бортики.
Чтобы ремень не проскальзывал, его нужно хорошо натянуть. Кто ездил на велосипеде хорошо знает проблему, что плохо натянутая цепь так и норовит слететь со звездочки, а если перетянешь – трудно ехать и она легко порвется. Для натяжения ремня или устранения его колебаний могут использоваться натяжные и прижимные ролики.
Диаметр ведущего шкива мы обозначим английской буквой d1, а ведомого — буквой d2. Нам это понадобится при расчетах.

Ремень является самым дешевым устройством в данном механизме. Но за счет него ремённая передача обеспечивает плавность хода и снижение шума. Такая передача способна амортизировать рывки и снижать нагрузку на мотор. Так, если на циркулярном станке резко заклинит диск при распиливании дубовой доски, электромотор остановится не сразу, а с задержкой за счет упругости ремня и его проскальзывания.
Рассмотрим следующую схему.

Ведущая ветвь ремня — та, которая набегает на ведущий шкив. Она при работе передачи испытывает растяжение.
Ведомая ветвь ремня — та, которая сходит с ведущего ремня и набегает на ведомый. Она при работе сжимается и расслабляется.
Сжатие и растяжение двух ветвей компенсируется. Иначе ремень рвется. При переходе с одной ветви на другую ремень упруго сжимается или растягивается. В этих зонах на шкиве происходит упругое скольжение ремня. Из-за изменения величины упругого скольжения передаточное отношение ремённой передачи непостоянное и может увеличиваться или уменьшаться в зависимости от нагрузки. При очень большой нагрузке ремень может упруго скользить по всей поверхности шкива.
Также важно знать про угол обхвата ремнём шкива. Чем больше угол обхвата, тем больше площадь контакта, тем больше полезная сила трения. При большой разнице в диаметрах шкивов этот угол может быть очень маленьким. Ремень при этом может проскальзывать. Чтобы увеличить угол обхвата без увеличения межосевого расстояния можно использовать прижимной ролик (смотри картинку ниже). В таком случае устанавливают ролик на ведомую ветвь, которая расслаблена, иначе ведущая ветвь растянется еще сильнее и износ ремня значительно вырастет.

Открытая, перекрестная и полуперекрестная передача

- В открытой ременной передаче шкивы расположены в одной плоскости параллельно друг-другу. Такая передача не меняет направления вращения ведомого шкива.
- В перекрестной ременной передаче приводной ремень закручен восьмеркой. Большой минус такого способа изменения направления вращения – большой износ ремня из-за дополнительного трения. Этот способ можно использовать при создании моделей из образовательного конструктора, но он редко используется в промышленных устройствах.
- В полуперекрестной ременной передаче ось вращения одного из шкивов повернута на некоторый угол относительно другой оси (например, на 90 градусов).
Повышающая и понижающая передача
Рассмотрим нижнюю картинку. Зеленый шкив с помощью ручки крутит персонаж с силой F. Это ведущий шкив. Синий шкив крутится за счет ремня. Это ведомый шкив. К нему на вал подвешен груз с максимально возможной массой, которую может поднять механизм.

- В первом случае диаметр ведущего и ведомого шкивов одинаковый. Скорость и сила на выходе не поменяется.
- Во втором случае диаметр ведущего шкива меньше ведомого. Скорость на выходе упадет. Такая передача называется понижающей. Сила при этом увеличится и механизм сможет поднять груз большей массы, чем первый.
- В третьем случае диаметр ведущего шкива больше ведомого. Скорость на выходе увеличится. Такая передача называется повышающей. Сила при этом уменьшится и механизм сможет поднять груз меньшей массы, чем первый и второй.
Почему так происходит? Любой сложный механизм можно представить через простые механизмы. В данном случае ручка, за которую тянет персонаж и радиус к точке на окружности, которую толкает приводной ремень, образуют рычаг. Посмотрите на следующий рисунок.

Короче плечо рычага к нагрузке (радиус шкива) – больше сила, но меньше пройденный путь.
Длиннее плечо рычага к нагрузке (радиус шкива) – меньше сила, но больше пройденный путь.
Эти схемы с понижающей и повышающей ремённой передачей наглядно демонстрируют работу золотого правила механики — за выигрыш в силе приходится платить таким же проигрышем в расстоянии (схема 1) или за выигрыш в расстоянии приходится платить таким же проигрышем в силе (схема 2).
Как посчитать передаточное отношение для ремённой передачи
При создании ремённой передачи нужно понимать, во сколько мы выиграем или проиграем в скорости и силе, чтобы собрать устройство с нужными характеристиками.
Передаточное отношение обозначается буквой i. Оно показывает, во сколько раз снизилась скорость вращения на выходе. Согласно золотому правилу механики, во столько же раз увеличится сила (крутящий момент).
Формулу для расчета передаточного отношения можно вывести из правила рычага. Передаточное отношение для ремённой передачи рассчитывается так:

Таким же образом передаточное отношение можно посчитать через соотношения радиусов.
Узнать размеры шкивов можно с помощью линейки. Самый точный метод измерения диаметра – с помощью штангенциркуля.

Передаточное отношение удобно записывать со знаком деления в виде i = 1 : 1. Эта запись показывает, что 1 оборот на входе даст 1 оборот на выходе. Передаточное отношение i = 5 : 1 показывает, что 5 оборотов на входе дает 1 оборот на выходе, то есть скорость упала в 5 раз (передача понижающая).
Если дробь можно сократить, её сокращают. Например, i = 5 : 25 = 1 : 5 (передача повышающая).
Передаточное число
Передаточное отношение можно записать в виде числа, поделив числитель на знаменатель. Например, i = 5 : 1 = 5, или i = 1 : 4 = 0,25. В данном случае говорят о передаточном числе.
Рассмотрим разные варианты передаточных чисел:

Передаточное отношение многоступенчатой ремённой передачи
Если передача многоступенчатая (двух-, трехступенчатая и т.д.), то общее передаточное отношение будет вычисляться как произведение отдельных передаточных отношений.

Эта формула справедлива для следующего рисунка:

Передаточное отношение для шкивов, жестко закрепленных на общей оси, не считается — скорость их вращения будет всегда одинаковой!
Виды приводных ремней
Видов ремней достаточно много, так как используются они в разных условиях. Где-то нужно передать очень большую мощность так, чтобы ремень не порвался и не растянулся. Где-то ремень не должен проскальзывать. Где-то ремень должен крутиться очень-очень быстро и мало изнашиваться со временем. А где-то нужно передать вращение на большое расстояние и под углом.
Очень распространенная классификация ремней – по поперечному сечению или форме. Основные виды: 1 — плоские ремни, 2 – клиновые ремни, 3 – ремни круглого сечения (пассики), 4 – многоручьевые ремни (или поликлиновые), 5 – зубчатые ремни.

В крупной промышленной технике самые распространенные ремни – клиновые и поликлиновые. Они достаточно толстые по сечению и имеют увеличенную за счет боковой поверхности площадь сцепления со шкивами.
В небольших электронных устройствах чаще используются плоские ремни и пассики (ремни с круглым сечением).

Плоские ремни широко использовались в 19-м и начале 20 века на фабриках для передачи движения на несколько машин с одного линейного вала (англ. line shaft). Они широко применялись и применяются в лесопильных станках, молотилках, электрогенераторах.
В станках с ЧПУ (3D-принтерах, плоттерах, лазерных станках) используются зубчатые ремни, так-так они сохраняют постоянное передаточное отношение и не проскальзывают.
Преимущества и недостатки ремённых передач
Как и у любого устройства, у ремённой передачи есть свои плюсы и минусы по сравнению с другими механизмами. Выделим важные из них.
Преимущества:
- простота конструкции;
- малая стоимость:
- малая шумность;
- плавность работы;
- сглаживание ударных перегрузок за счет упругости ремня;
- возможность менять направление вращения под разным углом;
- возможность передавать вращение на большое расстояние.
Недостатки:
- большие габариты конструкции;
- плохая работа на больших скоростях (появление вибраций);
- большая нагрузка на оси (валы, подшипники);
- непостоянное передаточное отношение при разной нагрузке (из-за упругого скольжения);
- малый срок службы ремня по сравнению с зубчатыми колесами;
- биение приводного ремня при его слабом натяжении;
- необходимость в дополнительных элементах при большой длине ремня или малом угле обхвата;
- увеличение износа приводного ремня или осей при неправильном натяжении.
Определения
- Ведущая ветвь ремня — набегает на ведущий шкив. При работе передачи растягивается.
- Ведомая ветвь ремня — сходит с ведущего ремня и набегает на ведомый. При работе передачи расслабляется.
- Межосевое (межцентровое) расстояние – кратчайшее расстояние между осями шкивов.
- Натяжной ролик (леникс, от нем. lenix, lenixrolle — натяжной ролик) – элемент ремённой или цепной передачи; свободно вращающееся на оси колесо (шкив, звездочка, ролик), которое используется для регулирования натяжения ремня или цепи. Например, используется в тракторах для натяжения гусениц или в двигателе автомобиля для натяжения ремня ГРМ (газораспределительного механизма).
- Пассик (от польского pasek — ремешок) – исторически вошедшее в наш оборот название приводного ремня круглого сечения. Слово «пассик» имеет польское происхождение. Его появление в русском словаре связывают с 80-ми годах 20-го века, когда им называли соответствующий элемент в импортном польском магнитофоне. Пассик, как правило, выполнен из резины или других полимерных материалов. Пассики использовались в устройстве протяжного механизма магнитной ленты старого кассетного магнитофона – он хорошо сглаживал рывки от электромотора и предохранял от искажений звука. «Пассики» входят в комплект конструктора Lego WeDo или ресурсного набора Lego MINDSTORMS Education EV3. В общем, всякий пассик — приводной ремень, но не каждый приводной ремень – пассик.
- Приводной ремень – гибкий замкнутый элемент (ремень) для передачи вращения между двумя шкивами. Вращение передается за счет силы трения (гладкий ремень) или силы зацепления (ремень с зубчиками). Может иметь разную форму: бывают плоские ремни, зубчатые ремни, клиновидные ремни.
- Ремённая передача (англ. belt drive)– механизм, предназначенный для передачи вращательного движения с помощью силы трения или зубчатого зацепления замкнутой гибкой связи (ремня) с помощью колес (шкивов), закрепленных на входном и выходном вале.
- Угол обхвата – угол прилегания ремня к шкиву.
- Шкив – фрикционное (англ. friction — трение) колесо с ободом или канавкой по окружности. Передает или принимает движение от приводного ремня. В отличие от блока, который имеет похожую форму, шкив всегда передавет усилие с оси на ремень, либо принимает усилие с ремня на ось. Блок же всегда свободно вращается на оси и обеспечивает изменение направления движения каната/троса, а также изменяет прикладываемую силу.
Вопросы
1. Что ты можешь сказать о ремённых передачах по этим двум изображениям? В чем их отличие и из каких элементов они состоят?

Задачи
1. Мальчик Ваня измерил штангенциркулем ведущий и ведомый шкив. Диаметр первого составил 12 миллиметров, второго – 32 миллиметра. Какое передаточное отношение у этой ремённой передачи?
2. Угловая скорость вращения вала мотора – 420 оборотов в секунду. Какая угловая скорость будет у ведомого шкива, если передаточное отношение i = 12 : 1?
3. Собери одноступенчатую понижающую ремённую передачу из деталей Lego. В качестве шкивов можно использовать диск узкого или большого колеса и желтые втулки. На ведущую ось установи ручку, на ось ведомого шкива установи стрелку, чтобы считать обороты.
Измерь с помощью линейки или штангенциркуля диаметры шкивов.
Заполни таблицу. Проверь опытным путем полученное значение с помощью стрелки.

4. Собери двухступенчатую понижающую ремённую передачу с ручкой и стрелкой (пример — в 3 задаче). Посчитай передаточное отношение через диаметры. Проверь полученное значение опытным путем.


Полезное видео
- Э+М. Ременная передача. Урок №3
- GetAClass. Золотое правило механики
- Анимация. Прямая и перекрестная ременная передача
- Анимация. Ременная передача — работы различных механизмов с помощью ремня
где N – мощность на ведущем шкиве Вт., n1 – частота
вращения ведущего шкива об/мин.
Полученный результат следует округлить до ближайшего значения по
стандартному ряду диаметров шкивов
(по ГОСТ 17383-73): 40; 45; 50; 56; 63; 71; 80; 90; 100; 112; 125;
140; 160; 180; 200; 224; 250; 280; 315; 355; 400; 450; 500; 560; 630; 710; 800;
900; 1000; 1120.
.2.2. Диаметр ведомого шкива с учётом относительного скольжения e (табл. 1.4)
|
Вид ремня |
e |
|
Прорезиненные и |
0.01 |
|
Кожаные |
0.015 |
|
Хлопчатобумажные |
0.01 |
![]()
Рассчитанное значение D2 округляем по стандартному ряду диаметров
шкивов.
Уточняем передаточное число:
![]()
Уточняем частоту вращения ведомого вала:
n2![]()
![]() n1/u (1-
n1/u (1-![]() )
)
Расхождение с заданным допускается до 3%.![]()
Определяем скорость ремня:
![]() м/сек
м/сек
Если V
получится меньше 10 м/с, то рекомендуется увеличить диаметры шкивов; при
техническом обосновании допустима и меньшая скорость.
Окружное усилие (H):
![]() , где N – мощность Вт, V-м/сек
, где N – мощность Вт, V-м/сек
Определяем межосевое расстояние a:
![]()
Угол обхвата на малом шкиве:
![]()
Он должен быть ![]() 150 0.
150 0.
Допускаемое полезное напряжение (удельное окружное усилие на
единицу площади поперечного сечения ремня):
![]() k0C0CaCp
k0C0CaCp
Значения k0
относящиеся к горизонтальным передачам, при D1=D2 (соответствует углам обхвата a=1800) при напряжении от
предварительного натяжения s0=1.8 Н/мм2 и скорости V=10 м/с даны в табл. 1.5.
Таблица 1.5 Значение k0 при V = 10 м/с, a = 180 0 и s0 = 1.8 Н/мм2
|
Отношение |
|||
|
прорезиненные |
кожаные |
хлопчатобумажные |
|
|
1/40 |
2.25 |
2.2 |
1.7 |
|
1/50 |
2.3 |
2.3 |
1.8 |
|
Примечание: При изменении |
Коэффициент C0 учитывает расположение
передачи. Для горизонтальных и наклонных до 600 передач C0 =1, при наклоне свыше 600
до 800 C0 =0.9, свыше 800 до
900 C0 =0.8.
Коэффициент Ca учитывает влияние угла обхвата
определяется по формуле:
![]()
Коэффициент, учитывающий влияние скорости:
![]()
Коэффициент CP учитывает условия эксплуатации передачи: при спокойной
работе с кратковременными пусковыми нагрузками не свыше 120% от номинальной, CP =1;
при умеренных колебаниях нагрузки и пусковой нагрузке до 150%, CP = =0.9;
при значительных колебаниях нагрузки и при пусковой нагрузке до
200%, CP =0.8;
при ударных нагрузках и пусковой нагрузке до 300%, CP =0.7.
При двухсменной работе значения CP брать на 0.1 меньше, при трёхсменной на
0.2 меньше.
Определяем площадь поперечного сечения ремня:
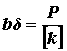 ,
,
где b –
ширина ремня мм, d –
толщина ремня мм.
Из условия:
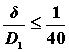 или
или  ,
,
определяем необходимую толщину ремня d. По таблицам 1.1., 1.2., 1.3. уточняем
толщину ремня. Следует учесть, что с уменьшением толщины ремня его
долговечность увеличивается.
По формуле:
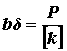
определяем b,
выбираем по таблицам 1.1.,
1.2., 1.3. ближайшее стандартное значение.
Примечание: некоторые уменьшение площади поперечного сечения ремня
по сравнению с полученным по расчёту допустимо, т.к. при уменьшении отношения d /D1 значение k0 возрастает.
Расчётная длина ремня (без учёта припуска на соединения концов):
![]() мм
мм
Число пробегов ремня в секунду:
![]() (с -1)
(с -1)
L в метрах (допускается для плоских ремней до 20 (1/с)).
Определяем силы, действующие в ремённой передаче.
Предварительное натяжение каждой ветви, Н
![]()
Натяжение ведущей ветви, в Н
![]()
Натяжение ведомой ветви, в Н
![]()
Проверяем окружное усилие:
![]()
Давление на вал, в Н
![]()
Максимальное начальное натяжение (с учётом последующего
ослабления) принимаем в 1.5 раза больше.
1.3 Шкивы плоскоремённых передач.
Материал для шкивов (при скорости ремня до 30 м/с) – чугун
марки не ниже СЧ 15 – 32. При большой скорости – до 45 м/с – шкивы отливают из
стали не ниже 25Л.
Ширину В обода шкива определяют в зависимости
от ширины ремня b (табл. 1.6).
Для предохранения от бокового скольжения ремня обод большого
шкива выполняют выпуклым, стрелу выпуклости определяют по табл. 1.7.
Рабочая поверхность обода должна иметь шероховатость
![]() .
.
Толщина обода у края ![]() .
.
Если шкив выполняется без спиц с диском, то толщину диска
принимают равной ![]() .
.
В конструкциях со спицами число их принимают в зависимости от
диаметра: при D£ 500 мм число спиц z = 4; при D свыше 500 до 1000 мм z = 6. Для широких шкивов при B> 300 мм число спиц удваивают и располагают их в два ряда. С
внутренней стороны обода для плавного перехода спиц делают кольцевой выступ
(рифт) высотой e
= s + 0.002B.
Спицы эллиптического сечения рассчитывают условно на изгиб от
окружного усилия Р, принимая во внимание одну треть их числа.
Таблица 1.6 Ширина обода шкива
|
b |
B |
b |
B |
b |
B |
|
|
40 50 63 71 80 90 |
50 63 71 80 90 100 |
100 112 125 140 160 180 |
112 125 140 160 180 200 |
200 224 250 280 315 355 |
234 250 280 315 355 400 |
|
|
400 |
||||||
Таблица 1.7 Стрела выпуклости у
|
Ширина обода B |
Диаметр шкива D, мм |
||||
|
250; 280 |
315; 355 |
400; 450 |
500; 600 |
630-1000 |
|
|
125 |
0.8 |
1 |
1 |
1 |
1 |
|
Св.125 до 160 |
0.8 |
1 |
1.2 |
1.5 |
1.5 |
|
Св.160 до 200 |
0.8 |
1 |
1.2 |
1.5 |
2 |
Расчётное сечение рассматривают условно в диаметральной
плоскости, проходящей через ось шкива перпендикулярно оси спицы; отношение осей
a:h=0.4; момент сопротивления одной спицы:
![]()
условие прочности:
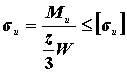
Для чугунных шкивов среднее значение ![]() . Размеры осей эллипса в сечении спицы у
. Размеры осей эллипса в сечении спицы у
обода уменьшают на 20%.
.3.8. Размеры ступицы шкива принимают в зависимости от диаметра
вала: L » (1.5+2) d, но по возможности не больше В;
d1 » (1.8+2) d.
2. Клиноремённые передачи
Промышленность выпускает клиновые ремни трёх видов: нормального
сечения, предназначенные для общего применения; допускаемая скорость до 30 м/с;
узкие – для скорости – до 40 м/с; широкие – для бесступенчатых передач
(вариаторов). Стандартные длины L
клиновых ремней, мм:
; 450; 500; 560; 630; 710; 800; 900; 1000; 1120; 1250; 1400; 1600;
1800; 2000; 2240; 2500; 2800; 3150; 4000; 4500; 5000; 5600; 6300; 7100; 8000;
9000; 10000; 11200; 12500; 14000; 16000; 18000.
Стандартные диаметры шкивов D, мм:
; 71; 80; 90; 100; 125; 140; 160; 180; 200; 224; 250; 280; 315;
355; 400; 450; 500; 560; 630; 710; 800; 900; 1000; 1120; 1400; 1600; 1800; 2000.
2.1 Расчёт клиноремённой передачи
Расчёт производят по следующим исходным данным: 1. Мощность на
ведущем валу. 2. Частота вращения ведущего вала. 3. Частота вращения ведомого
вала. 4. Передаточное число ремённой передачи. 5. Вращающий момент ведущего вала.
По номинальному моменту ведущего вала в таблице 2.1. выбирают
сечение ремня с площадью поперечного сечения ремня F и диаметром ведущего шкива Dmin. В табл. 2.1. указано минимальное
значение D1. Однако для обеспечения большей
долговечности ремня рекомендуется не ориентироваться на Dmin, а брать шкив на 1 – 2 номера больше.
Определяем (если не задано) передаточное число U без учёта скольжения:
![]()
Находим диаметр D2
ведомого шкива, с учётом относительного скольжения e (табл. 2.2.):
![]()
Выбираем ближайшее стандартное значение D2.
Уточняем передаточное число U с учётом e:
![]()
Пересчитываем:
![]()
Таблица 2.1. Клиновые ремни (по ГОСТ 1284 – 68)
|
|
|||||||||
|
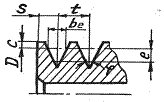
Тип |
Обозначение сечения |
Размеры сечения, мм |
F, мм2 |
L, м |
D1, мм |
T1, Нм |
|||
|
b |
be |
h |
y0 |
||||||
|
Нормального сечения |
О |
10 |
8.5 |
6 |
2.1 |
47 |
0.4-2.5 |
63 |
30 |
|
А |
13 |
11 |
8 |
2.8 |
81 |
0.56-4.0 |
90 |
15-60 |
|
|
Б |
17 |
14 |
10.5 |
4 |
138 |
0.8-6.3 |
125 |
50-150 |
|
|
В |
22 |
19 |
13.5 |
4.8 |
230 |
1.8-10 |
200 |
120-600 |
|
|
Г |
32 |
27 |
19 |
6.9 |
476 |
3.15-15 |
315 |
450-2400 |
|
|
Д |
38 |
32 |
23.5 |
8.3 |
692 |
4.5-18 |
500 |
1600-6000 |
|
|
Е |
50 |
42 |
30 |
11 |
1170 |
6.3-18 |
800 |
4000 |
|
|
Узкие |
УО |
10 |
8.5 |
8 |
2 |
56 |
0.63-3.55 |
63 |
150 |
|
УА |
13 |
11 |
10 |
2.8 |
95 |
0.8-4.5 |
90 |
90-400 |
|
|
УБ |
17 |
14 |
13 |
3.5 |
158 |
1.25-8 |
140 |
300-2000 |
|
|
УВ |
22 |
19 |
18 |
4.8 |
278 |
2-8 |
224 |
1500 |
Таблица 2.2. Относительное скольжение ремня
|
Тип ремня |
e |
|
Корд тканевый |
0.02 |
|
Корд шнуровой |
0.01 |
Определяем межосевое расстояние a: его выбираем в
интервале:

Принимаем близкое к среднему значению.
Расчётная длинна ремня определяется по формуле:
![]()
Выбираем ближайшую по стандартному ряду длину ремня.
Вычисляем среднее значение диаметра шкива:
![]()
Определяем новое значение a с учётом стандартной длинны L по формуле:
![]()
Примечание: при монтаже передачи необходимо обеспечить возможность
уменьшения a на 0.001L для того, чтобы облегчить надевание
ремней на шкив; для увеличения натяжения ремней необходимо предусмотреть
возможность увеличения a на 0.025L.
Угол обхвата меньшего шкива, в градусах:
Окружная скорость, м/с:
![]() D1n1/60000
D1n1/60000
По табл. 2.3 находим методом интерполяции величину окружного
усилия Р0, передаваемого одним клиновым ремнём при u=1, и длине L0.
Допускаемое окружное усилие на один ремень
![]() ,
,
где коэффициент, учитывающий влияние угла обхвата:
![]()
коэффициент, учитывающий влияние длины ремня:
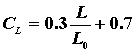
– коэффициент режима работы Ср, табл.
2.4.
Определяем окружное усилие, передаваемое ременной передачей
Н:
![]() , где N – Вт, V-м/сек
, где N – Вт, V-м/сек
Расчётное число ремней
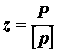
Определяем усилия в ремённой передачи, приняв напряжения от
предварительного натяжения s = 1.6 Н/мм2
Предварительное натяжение каждой ветви ремня Н:
![]() F – площадь сечения ремня
F – площадь сечения ремня
рабочее натяжение ведущей ветви
![]()
то же ведомой ветви
![]()
![]()
Таблица 2.3 Окружное усилие р0,
передаваемое одним клиновым ремнём при u=1, длине L0 и спокойной работе
|
Тип |
Сечение ремня (Длина L0), мм |
D1, мм |
V, м/с |
|||||||
|
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|||
|
Р0, Н |
||||||||||
|
Ремни нор – маль-ного сечения |
О (1320) |
71 |
112 |
95 |
81 |
68 |
56 |
– |
– |
– |
|
80 |
124 |
107 |
94 |
80 |
66 |
– |
– |
– |
||
|
90 |
134 |
116 |
104 |
86 |
76 |
62 |
– |
– |
||
|
100 |
140 |
124 |
111 |
98 |
84 |
66 |
– |
– |
||
|
А (1700) |
100 |
190 |
160 |
138 |
115 |
91 |
– |
– |
– |
|
|
112 |
210 |
182 |
160 |
137 |
112 |
83 |
– |
– |
||
|
125 |
230 |
200 |
177 |
155 |
132 |
105 |
– |
– |
||
|
140 |
246 |
218 |
194 |
172 |
148 |
121 |
– |
– |
||
|
160 |
264 |
135 |
214 |
190 |
165 |
138 |
– |
– |
||
|
Б (2240) |
140 |
322 |
270 |
230 |
191 |
– |
– |
– |
– |
|
|
160 |
366 |
315 |
275 |
236 |
196 |
149 |
– |
– |
||
|
180 |
402 |
351 |
310 |
272 |
230 |
184 |
– |
– |
||
|
200 |
430 |
379 |
238 |
300 |
257 |
212 |
– |
– |
||
|
224 |
452 |
405 |
363 |
325 |
282 |
271 |
– |
– |
||
|
В (3750) |
224 |
630 |
535 |
463 |
393 |
318 |
235 |
– |
– |
|
|
250 |
696 |
602 |
530 |
460 |
384 |
302 |
– |
– |
||
|
280 |
756 |
663 |
590 |
520 |
44 |
383 |
– |
– |
||
|
315 |
814 |
719 |
647 |
558 |
500 |
416 |
– |
– |
||
|
355 |
864 |
770 |
700 |
630 |
550 |
470 |
– |
– |
||
|
Г (6000) |
355 |
1350 |
1140 |
990 |
840 |
680 |
513 |
– |
– |
|
|
400 |
1510 |
1300 |
1150 |
100 |
840 |
670 |
– |
– |
||
|
450 |
1650 |
1440 |
1290 |
1140 |
980 |
816 |
– |
– |
||
|
500 |
1760 |
1550 |
1400 |
1250 |
1100 |
926 |
– |
– |
||
|
560 |
1850 |
1660 |
1500 |
1350 |
1180 |
1300 |
– |
– |
||
|
Д (7100) |
560 |
2280 |
1990 |
1760 |
1550 |
1930 |
1090 |
– |
– |
|
|
630 |
2480 |
2180 |
1960 |
1740 |
1840 |
1280 |
– |
– |
||
|
710 |
2640 |
2350 |
2120 |
1910 |
1690 |
1440 |
– |
– |
||
|
800 |
2800 |
2500 |
2280 |
2060 |
1520 |
1590 |
– |
– |
||
|
900 |
2920 |
2600 |
2400 |
2190 |
1330 |
1720 |
– |
– |
||
|
Ремни узкие |
УО (1600) |
71 |
236 |
195 |
164 |
136 |
106 |
– |
– |
– |
|
80 |
276 |
234 |
204 |
175 |
146 |
– |
– |
– |
||
|
90 |
310 |
265 |
238 |
210 |
180 |
152 |
– |
– |
||
|
100 |
332 |
292 |
263 |
236 |
208 |
178 |
– |
– |
||
|
УА (2500) |
100 |
378 |
315 |
269 |
– |
– |
– |
– |
||
|
112 |
434 |
372 |
325 |
280 |
233 |
– |
– |
– |
||
|
125 |
492 |
423 |
378 |
330 |
280 |
236 |
– |
– |
||
|
140 |
528 |
470 |
420 |
378 |
330 |
281 |
226 |
– |
||
|
160 |
576 |
517 |
468 |
427 |
380 |
331 |
276 |
220 |
||
|
УБ (3535) |
140 |
590 |
500 |
425 |
– |
– |
– |
– |
– |
|
|
160 |
690 |
600 |
526 |
455 |
376 |
– |
– |
– |
||
|
180 |
760 |
670 |
603 |
530 |
456 |
383 |
– |
– |
||
|
200 |
824 |
730 |
667 |
595 |
524 |
443 |
360 |
– |
||
|
224 |
852 |
790 |
710 |
650 |
594 |
503 |
423 |
– |
||
|
УВ (5600) |
224 |
1090 |
940 |
820 |
705 |
– |
– |
– |
– |
|
|
250 |
1210 |
1060 |
946 |
830 |
704 |
570 |
– |
– |
||
|
280 |
1320 |
1150 |
1090 |
935 |
820 |
690 |
– |
– |
||
|
315 |
1410 |
1280 |
1160 |
1045 |
928 |
796 |
649 |
500 |
||
|
355 |
1520 |
1380 |
1250 |
1145 |
1020 |
890 |
846 |
585 |
Таблица 2.4. Коэффициент динамичности режима работы Ср
|
Режим работы |
Cp |
|
Нагрузка спокойная |
1 |
|
Умеренные колебания |
1.1 |
|
Значительные колебания |
1.25 |
|
Ударные и резко неравномерные нагрузки |
1.5; 1.6 |
|
При частых и резких пусках |
повысить на 0.1 |
2.2 Шкивы клиноремённых передач
Материал шкивов – чугун СЧ 15 – 32, сталь 25Л.
Шероховатость рабочих поверхностей Rz £ 2.5 мкм.
Стандартные диаметры шкивов, профили канавок для ремней
нормального сечения и их размеры приведены в разделе 2.
Шкивы выполняют дисковыми, если их расчётный диаметр не
превышает следующих значений, мм:
|
для ремней О |
до 160 |
|
для ремней А |
до 200 |
|
для ремней Б |
до 250 |
|
для ремней В |
до 355 |
|
для ремней Г |
до 400 |
Шкивы большего диаметра, а также шкивы для ремней Д и Е
выполняют со спицами.
Канавки шкивов для клиновых ремней нормального сечения
представлены в табл. 2.5.
Таблица 2.5 Канавки шкивов для клиновых ремней нормального
сечения. Размеры, мм
|
|
||||||||
|
Сечение ремня |
С |
е |
t |
s |
Расчётные диаметры при угле j 0 |
|||
|
34 |
36 |
38 |
40 |
|||||
|
О |
2.5 |
7.5 |
12 |
8 |
63-71 |
80-100 |
112-160 |
180 |
|
А |
3.3 |
9 |
15 |
10 |
90-112 |
125-160 |
180-400 |
450 |
|
Б |
4.2 |
11 |
19 |
12.5 |
125-160 |
180-224 |
250-500 |
560 |
|
В |
5.7 |
14.5 |
22.5 |
17 |
– |
200-315 |
355-630 |
710 |
|
Г |
8.1 |
20 |
37 |
24 |
– |
315-450 |
500-900 |
1000 |
|
Д |
9.6 |
23.5 |
44.5 |
29 |
– |
500-560 |
630-1120 |
1250 |
|
Е |
12.5 |
31 |
58 |
38 |
– |
– |
800-1400 |
1600 |
Таблица 3.1. Поликлиновые ремни. Размеры, мм
|
|
|||||||||
|
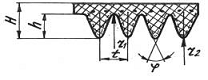
Сечение ремня |
t |
H |
h |
r1 |
r2 |
Длина |
D1 |
M1, Hм |
Масса (кг) 1 м ремня с 10 рёбрами |
|
К |
2.4 |
4 |
2.35 |
0.1 |
0.4 |
400-2000 |
40 |
40 |
0.09 |
|
Л |
4.8 |
9.5 |
4.85 |
0.2 |
0.7 |
1250-4000 |
80 |
18-400 |
0.45 |
|
М |
9.5 |
16.7 |
10.35 |
0.4 |
1.0 |
2000-4000 |
180 |
³130 |
1.6 |
|
Примечания: 1. Стандартные длины поликлиновых |
3.
Поликлиновые ремни
По сравнению с клиновыми поликлиновые ремни более гибки,
поэтому для них можно применять шкивы меньшего диаметра, следовательно,
габариты передачи уменьшаются; нагрузка по ширине ремня распределяется равномерно,
тогда как в передачах с клиновыми ремнями необходимо тщательно подбирать ремни
по длине для обеспечения одинакового натяжения.
3.1 Расчёт поликлиновой передачи
Выбрать поперечное сечение поликлинового ремня, в зависимости
от момента ведущего вала по табл. 3.1.
Определяем диаметр меньшего шкива, при вращающем моменте на
ведущем валу M1 £ 250 Н×м
![]()
при М1=260 ¸900 Н×м, ![]() , здесь D1 в мм.
, здесь D1 в мм.
Полученный результат округляют по стандарту (см. раздел 2).
Находят D2,
округляют его также, уточняют передаточное отношение (с учётом относительного
скольжения e)
и частоту вращения ведомого шкива.
Межосевое расстояние a принимают в зависимости от u и отношения 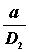 ;
;
|
u |
1 – 2 |
Cв.2 до 3 |
Св.3 до 6 |
|
|
Определяют расчётную длину L ремня, округляют до
стандартного значения.
Пересчитать межосевое расстояние по формуле:
![]()
Требуемое число рёбер поликлинового ремня:
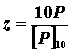
где
![]()
Здесь Р10 – окружное усилие, передаваемое
поликлиновым ремнём с 10 рёбрами при i = 1, a1 = 180 0, длине L0 и спокойной работе в одну смену. Значение
Р10 приведены в таблице (3.2). Коэф. Сa, учитывающий влияние угла обхвата,
определяют по формуле: ![]() .
.
Коэф. СL, учитывающий длину ремня определяют в
зависимости от отношения L/L0, где L0 – эталонная длина, указана в табл. 3.2:
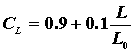
Коэф. режима работы СР принимают
таким же, как и для плоскоремённой передачи (см. раздел 1).
Поправка 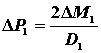 учитывает уменьшение напряжения изгиба
учитывает уменьшение напряжения изгиба
ремня на большом шкиве по сравнению с тем, которая возникает при изгибе на
малом шкиве: здесь DР1 в Н; D1
в м; DM1 в Н×м (табл. 3.3).
Если число рёбер получается больше рекомендуемого (см. прим.
3 к табл. 3.1), то следует увеличить диаметры шкивов, повысив тем самым
окружную скорость и соответственно снизив расчётное окружное усилие.
Дальнейший расчёт выполняют так же, как и для клиноремённой
передачи.
Таблица 3.2. Значение Р10 для поликлиновых
ремней с 10 рёбрами при u = 1, a = 180 0, длине L0 и спокойной работе в
одну смену
|
Сечение ремня |
D1, мм |
Значение Р10, Н, при окружной |
|||||
|
5 |
10 |
15 |
20 |
25 |
30 |
||
|
К (L0=710 |
40 |
280 |
240 |
214 |
185 |
– |
– |
|
50 |
330 |
290 |
266 |
240 |
212 |
– |
|
|
63 |
380 |
340 |
307 |
285 |
256 |
227 |
|
|
71 |
400 |
360 |
326 |
300 |
276 |
247 |
|
|
80 |
410 |
370 |
346 |
320 |
263 |
||
|
90 |
430 |
390 |
358 |
335 |
308 |
280 |
|
|
100 |
440 |
400 |
373 |
345 |
320 |
290 |
|
|
112 |
450 |
410 |
386 |
360 |
328 |
303 |
|
|
125 |
460 |
420 |
400 |
375 |
348 |
317 |
|
|
140 |
470 |
430 |
412 |
380 |
352 |
320 |
|
|
160 |
480 |
440 |
412 |
385 |
360 |
340 |
|
|
Л (L0=1600 мм) |
80 |
780 |
640 |
527 |
415 |
– |
– |
|
100 |
1000 |
860 |
746 |
635 |
520 |
– |
|
|
112 |
1100 |
960 |
846 |
735 |
612 |
– |
|
|
125 |
1180 |
1040 |
925 |
815 |
690 |
570 |
|
|
140 |
1260 |
1100 |
1000 |
890 |
770 |
630 |
|
|
160 |
1340 |
1200 |
1076 |
970 |
850 |
717 |
|
|
180 |
1400 |
1260 |
1130 |
1030 |
910 |
780 |
|
|
200 |
1440 |
1300 |
1190 |
1080 |
960 |
827 |
|
|
224 |
1500 |
1350 |
1240 |
1130 |
1010 |
870 |
|
|
250 |
1540 |
1400 |
1280 |
1170 |
1050 |
917 |
|
|
280 |
1580 |
1430 |
1310 |
1200 |
1090 |
953 |
|
|
315 |
1600 |
1470 |
1350 |
1240 |
1120 |
990 |
|
|
355 |
1640 |
1500 |
1380 |
1280 |
1160 |
1020 |
|
|
М (L0=2240 мм) |
180 |
2900 |
2400 |
2010 |
1640 |
1270 |
807 |
|
200 |
3260 |
2770 |
2380 |
2015 |
1616 |
1180 |
|
|
224 |
3600 |
3130 |
2740 |
2375 |
1980 |
1540 |
|
|
250 |
3940 |
3440 |
3050 |
2690 |
2280 |
1870 |
|
|
280 |
4200 |
3740 |
3350 |
2990 |
2600 |
2130 |
|
|
315 |
4300 |
4000 |
3620 |
3250 |
2840 |
2400 |
|
|
355 |
4740 |
4240 |
3870 |
3500 |
3120 |
2660 |
|
|
400 |
4960 |
4460 |
4070 |
3700 |
3320 |
2870 |
|
|
450 |
5140 |
4650 |
4270 |
3900 |
3480 |
3060 |
|
|
500 |
5300 |
4780 |
4400 |
4050 |
3640 |
3200 |
|
|
630 |
5600 |
5070 |
4660 |
4350 |
3920 |
3500 |
|
|
800 |
5800 |
5310 |
4930 |
4550 |
4160 |
3730 |
|
|
1000 |
5960 |
5410 |
5070 |
4700 |
4320 |
3900 |
Таблица 3.3. Значения DМ1, Н×м, для поликлиновых ремней
|
Сечение ремня |
||||||
|
1 |
1.1 |
1.25 |
1.5 |
2 |
2.5 |
|
|
К |
0 |
0.2 |
0.4 |
0.5 |
0.6 |
0.7 |
|
Л |
0 |
1.8 |
3.6 |
4.5 |
5.0 |
5.4 |
|
М |
0 |
13.8 |
27.6 |
34.5 |
38.0 |
41.4 |
Список
литературы
1.
Иванов М.Н. «Детали машин»: Учебник для студентов высших технических учебных
заведений. – 5-е изд. Переработанное. – М. Высш. школа. 1991. – 383 ст.
.
Решетев Д.Н. «Детали машин»: Учебник для студентов машиностроительных и
механических специальностей вузов. – 4-е изд. Переработанное и дополн. – М.
Машиностроение. 1989 – 436 с.
.
Чернавский, Ицкович и др.: «Курсовое проектирование деталей машин».
Классификация передач. В зависимости от формы поперечного сечения ремня передачи бывают: плоскоременные, клиноременные, круглоременные, поликлиноременные (рис. 69). Плоскоременные передачи по расположению бывают перекрестные и полуперекрестные (угловые), рис. 70. В современном машиностроении наибольшее применение имеют клиновые и поликлиновые ремни. Передача с круглым ремнем имеет ограниченное применение (швейные машины, настольные станки, приборы).
Разновидность ременной передачи является Зубчатоременная, передающая нагрузку путем зацепления ремня со шкивами.
|
|
|
||
|
А |
Б |
||
|
Рис. 69. Виды приводных ремней: а – плоский, б – клиновой, в – поликлиновой, г – круглый. |

Рис. 70. Виды плоскоременных передач: а – перекрестная, Б – полуперекрестная (угловая)
Назначение. Ременные передачи относится к механическим передачам трения с гибкой связью и применяют в случае если необходимо передать нагрузку между валами, которые расположены на значительных расстояниях и при отсутствии строгих требований к передаточному отношению. Ременная передача состоит из ведущего и ведомого шкивов, расположенных на некотором расстоянии друг от друга и соединенных ремнем (ремнями), надетым на шкивы с натяжением. Вращение ведущего шкива преобразуется во вращение ведомого благодаря трению, развиваемому между ремнем и шкивами. По форме поперечного сечения различают Плоские, Клиновые, Поликлиновые и Круглые приводные ремни. Различают плоскоременные передачи – Открытые, которые осуществляют передачу между параллельными валами, вращающимися в одну сторону; Перекрестные, Которые осуществляют передачу между параллельными валамиПри вращении шкивов в противоположных направлениях; в Угловых (полуперекрестных) плоскоременных передачах шкивы расположены на скрещивающихся (обычно под прямым углом) валах. Для обеспечения трения между шкивом и ремнем создают натяжение ремней путем предварительного их упругого деформирования, путем перемещения одного из шкивов передачи или с помощью натяжного ролика (шкива).
Преимущества. Благодаря эластичности ремней передачи работают плавно, без ударов и бесшумно. Они предохраняют механизмы от перегрузки вследствие возможного проскальзывания ремней. Плоскоременные передачи применяют при больших межосевых расстояниях и, работающие при высоких скоростях ремня (до 100М/с). При малых межосевых расстояниях, больших передаточных отношениях и передаче вращения от одного ведущего шкива к нескольким ведомым предпочтительнее клиноременные передачи. Малая стоимость передач. Простота монтажа и обслуживания.
Недостатки. Большие габариты передач. Изменение передаточного отношения из-за проскальзывания ремня. Повышенные нагрузки на опоры валов со шкивами. Необходимость устройств для натяжения ремней. Невысокая долговечность ремня.
Сферы применения. Плоскоременная передача проще, но клиноременная обладает повышенной тяговой способностью и вписывается в меньшие габариты.
Поликлиновые ремни – плоские ремни с продольными клиновыми выступами-ребрами на рабочей поверхности, входящими в клиновые канавки шкивов. Эти ремни сочетают достоинства плоских ремней – гибкость и клиновых – повышенную сцепляемость со шкивами.
Круглоременные передачи применяют в небольших машинах, например машинах швейной и пищевой промышленности, настольных станках, а также различных приборах.
По мощности ременные передачи применяются в различных машинах и агрегатах при ![]() 50КВТ, (в некоторых передачах до 5000КВт), при окружной скорости –
50КВТ, (в некоторых передачах до 5000КВт), при окружной скорости – ![]() 40М/с, (в некоторых передачах до 100М/с), по передаточным числам
40М/с, (в некоторых передачах до 100М/с), по передаточным числам ![]() 15, КПД передач: плоскоременные
15, КПД передач: плоскоременные ![]() 0,93…0,98, а клиноременные –
0,93…0,98, а клиноременные – ![]() 0,87…0,96.
0,87…0,96.

Рис. 71 Схема ременной передачи.
Силовой расчет. Окружная сила на ведущем шкиве
 . (12.1)
. (12.1)
Расчет ременных передач выполняют по расчетной окружной силе с учетом коэффициента динамической нагрузки ![]() И режима работы передачи:
И режима работы передачи:
 , (12.2)
, (12.2)
Где ![]() – коэффициент динамической нагрузки, который принимается
– коэффициент динамической нагрузки, который принимается ![]() =1 при спокойной нагрузке,
=1 при спокойной нагрузке, ![]() =1,1 – умеренные колебания нагрузки,
=1,1 – умеренные колебания нагрузки, ![]() =1.25 – значительные колебания нагрузки,
=1.25 – значительные колебания нагрузки, ![]() =1,5 – ударные нагрузки.
=1,5 – ударные нагрузки.
Начальную силу натяжения ремня FO (предварительное натяжение) принимают такой, чтобы ремень мог сохранять это натяжение достаточно длительное время, не подвергаясь большой вытяжке и не теряя требуемой долговечности. Соответственно этому начальное напряжение в ремне для плоских стандартных ремней без автоматических натяжных устройств ![]() =1,8МПа; с автоматическими натяжными устройствами
=1,8МПа; с автоматическими натяжными устройствами ![]() = 2МПа; для клиновых стандартных ремней
= 2МПа; для клиновых стандартных ремней ![]() =1,2…1,5МПа; для полиамидных ремней
=1,2…1,5МПа; для полиамидных ремней ![]() = 3…4МПа.
= 3…4МПа.
Начальная сила натяжения ремня
![]() , (12.3)
, (12.3)
Где А – Площадь поперечного сечения ремня плоскоременной передачи либо площадь поперечного сечения всех ремней клиноременной передачи.
Силы натяжения ведущей ![]() И ведомой S2 Ветвей ремня в нагруженной передаче можно определить из условия равновесия шкива (рис. 72).
И ведомой S2 Ветвей ремня в нагруженной передаче можно определить из условия равновесия шкива (рис. 72).

Рис. 72. Схема к силовому расчету передачи.
Из условия равновесия ведущего шкива
 (12.4)
(12.4)
С учетом (12.2) окружная сила на ведущем шкиве
![]() . (12.5)
. (12.5)
Натяжение ведущей ветви
 , (12.6)
, (12.6)
Натяжение ведомой ветви
 . (12.7)
. (12.7)
Давление на вал ведущего шкива
 . (12.8)
. (12.8)
Зависимость между силами натяжения ведущей и ведомой ветвей приближенно определяют по формуле Эйлера, согласно которой натяжений концов гибкой, невесомой, нерастяжимой нити, охватывающей барабан связаны зависимостью
![]() , (12.9)
, (12.9)
Где ![]() – коэффициент трения между ремнем и шкивом,
– коэффициент трения между ремнем и шкивом, ![]() – угол обхвата шкива.
– угол обхвата шкива.
Среднее значение коэффициента трения для чугунных и стальных шкивов можно принимать: для резинотканевых ремней ![]() =0,35, для кожаных ремней
=0,35, для кожаных ремней ![]() = 0,22 и для хлопчатобумажных и шерстяных ремней
= 0,22 и для хлопчатобумажных и шерстяных ремней ![]() = 0,3.
= 0,3.
При определении сил трения в клиноременной передаче в формулы вместо – коэффициента, трения ![]() надо подставлять приведенный коэффициент трения для клиновых ремней
надо подставлять приведенный коэффициент трения для клиновых ремней
 , (12.10)
, (12.10)
Где ![]() – угол клина ремня
– угол клина ремня ![]() .
.
При совместном рассмотрении приведенных силовых соотношений для ремня получим окружную силу на ведущем шкиве
![]() , (12.11)
, (12.11)
Где ![]() – коэффициент тяги, который определяется по зависимости
– коэффициент тяги, который определяется по зависимости
 . (12.12)
. (12.12)
Увеличение окружного усилия на ведущем шкиве можно достичь увеличением предварительного натяжения ремня либо повышением коэффициента тяги, который повышается с увеличением угла обхвата и коэффициента трения.
В таблицах со справочными данными по характеристикам ремней указаны их размеры с учетом необходимых коэффициентов тяги.
Геометрический расчет. Расчетная длина ремней при известном межосевом расстоянии и диаметрах шкивов (рис.71):
![]() (12.13)
(12.13)
Где ![]() . Для конечных ремней длину
. Для конечных ремней длину ![]() окончательно согласовывают со стандартными длинами по ГОСТ. Для этого выполняют геометрический расчет согласно схемы показанной на рис.73.
окончательно согласовывают со стандартными длинами по ГОСТ. Для этого выполняют геометрический расчет согласно схемы показанной на рис.73.

Рис.73. Схема к геометрическому расчету ременной передачи
По окончательно установленной длине ![]() плоскоременной или клиноременной открытой передачи действительное межосевое расстояние передачи пои условии, что
плоскоременной или клиноременной открытой передачи действительное межосевое расстояние передачи пои условии, что ![]()
![]()
Расчетные формулы без учета провисания и начальной деформации ремня.
Угол обхвата ведущего шкива ремнем в радианах:
 , (12.14)
, (12.14)
В градусах  .
.
Для плоскоременной передачи рекомендуется ![]() , а для клиноременной
, а для клиноременной ![]() .
.
Порядок выполнения проектного расчета. Для ременной передачи при проектном расчете по заданным параметрам (мощность, момент, угловая, скорость и передаточное отношение) определяются размеры ремня и приводного шкива, которые обеспечивают необходимую усталостную прочность ремня и критический коэффициент тяги при максимальном КПД. По выбранному диаметру ведущего шкива из геометрического расчета определяются остальные размеры: ![]()
Проектный расчет плоскоременной передачи по тяговой способности производят по допускаемому полезному напряжению, Которое определяют по кривым скольжения. В результате расчета определяется ширина ремня по формуле:
 , (12.15)
, (12.15)
Где ![]() – окружная сила в передаче;
– окружная сила в передаче; ![]() – допустимая удельная окружная сила, которая соответствует максимальному коэффициенту тяги, которая определяется при скорости ремня
– допустимая удельная окружная сила, которая соответствует максимальному коэффициенту тяги, которая определяется при скорости ремня ![]() =10 м/с и угле обхвата
=10 м/с и угле обхвата ![]() =1800;
=1800; ![]() – коэффициент расположения передачи в зависимости от угла наклона
– коэффициент расположения передачи в зависимости от угла наклона ![]() линии центров к горизонтальной линии:
линии центров к горизонтальной линии: ![]() =1,0, 0,9, 0,8 для углов наклона
=1,0, 0,9, 0,8 для углов наклона ![]() =0…600, 60…800, 80…900;
=0…600, 60…800, 80…900; ![]() – коэффициент угла обхвата шкива
– коэффициент угла обхвата шкива ![]() ;
; ![]() – скоростной коэффициент:
– скоростной коэффициент: ![]() ;
; ![]() – коэффициент режима работы, который принимается:
– коэффициент режима работы, который принимается: ![]() =1,0 спокойная нагрузка;
=1,0 спокойная нагрузка; ![]() =0,9 нагрузка с небольшими изменениями,
=0,9 нагрузка с небольшими изменениями, ![]() =0,8 – нагрузка с большими колебаниями,
=0,8 – нагрузка с большими колебаниями, ![]() =0,7 – ударные нагрузки.
=0,7 – ударные нагрузки.
Для расчета предварительно по эмпирическим формулам определяется диаметр ведущего шкива
 , (12.16)
, (12.16)
Где ![]() – передаваемая мощность в кВт,
– передаваемая мощность в кВт, ![]() – частота вращения.
– частота вращения.
Диаметр ведущего шкива округляется до ближайшего стандартного.
Принимается тип ремня, по которому определяется ![]() допустимая удельная окружная сила по таблице 12.1.
допустимая удельная окружная сила по таблице 12.1.
Таблица 12.1
Параметры плоских приводных ремней
|
Параметры |
Марка ткани для прокладок ремня |
||||
|
Б-800 |
БКНЛ-65 |
ТК-150 |
ТК-200-2 |
ТК-300 |
|
|
Допустимая действующая сила на прокладку, Н/мм |
3 |
3 |
10 |
13 |
20 |
|
Расчетная толщина тканевой прокладки Δ мм |
1,5 |
1,5 |
1,3 |
1,4 |
1,5 |
|
Число прокладок Zn |
3…6 |
3…6 |
3,4 3…5, при b = 355мм |
3,4 |
3,0 b = 180…315мм |
Расчетную ширину ремня округляют до ближайшей стандартной ширины по табл.12.2.
Таблица 12.2 Стандартная ширина плоских приводных ремней
|
1-й ряд |
20, 25,32, 40, 50, 63, 71, 80, 90, 110, 112, 125, 140, 160, 180, 200, 224, 250, 280… |
|
2-й ряд |
30, 60, 70, 115, 300… |
Таблица 12.3 Ширина обода шкива плоскоременной передачи.
|
B |
В |
B |
В |
B |
В |
|
40 |
50 |
100 |
112 |
200 |
224 |
|
50 |
63 |
112 |
125 |
224 |
250 |
|
63 |
71 |
125 |
140 |
250 |
280 |
|
71 |
80 |
140 |
160 |
280 |
315 |
|
80 |
90 |
160 |
180 |
315 |
355 |
|
90 |
100 |
180 |
200 |
355 |
400 |
|
400 |
450 |
Проектный расчет клиноременной передачи по тяговой способности производят по допускаемой мощности передаваемой одним ремнем выбранного поперечного сечения, которое также определяют по кривым скольжения. В результате расчета определяется количество ремней выбранного сечения по формуле:
 , (12.17)
, (12.17)
Где ![]() – допускаемая мощность, передаваемой одним поперечного сечения;
– допускаемая мощность, передаваемой одним поперечного сечения; ![]() – коэффициент угла обхвата шкива:
– коэффициент угла обхвата шкива: ![]() ;
; ![]() – коэффициент длины ремня:
– коэффициент длины ремня: ![]() ;
; ![]() – коэффициент, который учитывает неравномерность нагружения между ремнями
– коэффициент, который учитывает неравномерность нагружения между ремнями ![]() .
.
Для расчета по формуле (12.17) предварительно по эмпирическим зависимостям определяется тип поперечного сечения ремня (рис.74), а по нему предварительно принимается диаметр ведущего шкива по передаваемой мощности и частоте вращения, согласно таблице 12.3.
Таблица 12.4
Мощность N0, которая передается одним клиновым ремнем при α=180o, длине ремня ℓ0 спокойном нагружении и передаточном отношении U = 1
|
Сечение ремня |
Диаметр d1, мм |
Р0 (кВт) при скорости ремня υ, м/с |
|||||
|
3 |
5 |
10 |
15 |
20 |
25 |
||
|
Z l0=1320мм |
63 71 80 90 100 |
0,31 0,37 0,40 0,44 0,46 |
0,49 0,56 0,62 0,67 0,70 |
0,82 0,95 1,07 1,16 1,24 |
1,03 1,22 1,41 1,56 1,67 |
1,11 1,37 1,60 1,73 1,97 |
– 1,40 1,65 1,90 2,10 |
|
А l0=1700мм |
90 100 112 125 140 |
0,56 0,62 0,70 0,74 0,80 |
0,84 0,95 1,05 1,15 1,23 |
1,39 1,60 1,82 2,00 2,18 |
1,75 2,07 2,39 2,66 2,91 |
1,88 2,31 2,74 3,10 3,44 |
– 2,29 2,82 3,27 3,70 |
|
В l0=2240мм |
125 140 160 180 200 224 |
0,92 1,07 1,20 1,30 1,40 1,47 |
1,39 1,61 1,83 2,01 2,15 2,26 |
2,26 2,70 3,15 3,51 3,79 4,05 |
2,80 3,45 4,13 4,66 5,08 5,45 |
– 3,38 4,73 5,44 6,00 6,50 |
– – 4,88 5,76 6,43 7,05 |
|
С l0=3750мм |
200 224 250 280 |
1,85 2,08 2,28 2,46 |
2,77 3,15 3,48 3,78 |
4,58 5,35 6,02 6,63 |
5,80 6,95 7,94 8,86 |
6,33 7,86 9,18 10,4 |
– 7,95 9,60 11,1 |
|
D l0=6000мм |
355 400 450 500 |
4,46 4,94 5,36 5,70 |
6,74 7,54 8,24 8,80 |
11,4 13,3 14,4 15,5 |
14,8 17,2 19,3 21,0 |
16,8 20,0 22,3 25,0 |
17,1 21,1 24,6 27,5 |
Перевод системы обозначений сечений клиновых ремней по ГОСТ 1284 в международные стандарты: О – Z, А – A, Б – B, В – C, Г – D, Д – E, Е – E0
Межосевое расстояние может быть задано в исходных данных, либо приниматься в диапазоне
![]() ,
,
![]() ,
,
Где ![]() – высота, выбранного сечения ремня.
– высота, выбранного сечения ремня.
В результате геометрического расчета передачи уточняются значения параметров определяются расчетная длина ремня ![]() , которая округляется до ближайшего стандартного значения, согласно таблице 12.5.Таблица 12.5
, которая округляется до ближайшего стандартного значения, согласно таблице 12.5.Таблица 12.5
Стандартная длина клиновых ремней
|
Длина |
Сечение ремня |
|||
|
Z |
A |
B |
C |
|
|
400; 425; 450; 475; 500; 530 |
* | |||
|
560; 600; 630; 670; 710; 750 |
* | * | ||
|
800; 850; 900; 950; 1000; 1060 |
* | * | * | |
|
1120; 1180; 1250; 1320; 1400; 1500; 1600; 1700; 1800; 1900; 2000; 2120; 2240; 2360;2500 |
* | * | * | * |
|
2650; 2800; 3000; 3150; 3350; 3550; 3750; 4000 |
* | * | * | |
|
4250; 4500; 4750; 5000; 5300; 5600; 6000 |
* | * | ||
|
6300; 6700; 7100; 7500; 8000; 8500; 9000; 9500; 10000; 10600 |
* |
Расчетное число клиновых ремней округляют до ближайшего большего целого числа.
Проверочный расчет на долговечность. Долговечность ремня определяется его сопротивлением усталости при циклическом нагружении. Сопротивление усталости определяется числом циклов нагружений, которое возрастает с увеличением при скорости ремня и уменьшении его длины. Для обеспечения долговечности ремня в пределах 1000…5000 часов работы проверяется число пробегов ремня в секунду, которое соответствует числу нагружений в секунду
 , (12.18)
, (12.18)
Где ![]() – скорость ремня,
– скорость ремня, ![]() – длина ремня;
– длина ремня; ![]() – допустимое число пробегов ремня в секунду. Рекомендовано для плоских ремней
– допустимое число пробегов ремня в секунду. Рекомендовано для плоских ремней ![]() =5 с-1, а для клиновых ремней
=5 с-1, а для клиновых ремней ![]() =15 с-1.
=15 с-1.
Таблица 12.6
Размеры канавок шкива клиноременной передачи

|
Сечение ремня |
c |
e |
t |
Расчетные диаметры при угле φо |
||||
|
34 |
36 |
38 |
40 |
|||||
|
Z |
2,5 |
7,5 |
12,0 |
8,0 |
63-71 |
80-100 |
112-160 |
180 |
|
A |
3,3 |
9,0 |
15,0 |
10,0 |
90-112 |
125-160 |
180-400 |
450 |
|
B |
4,2 |
11,0 |
19,0 |
12,5 |
125-160 |
180-224 |
250-500 |
560 |
|
C |
5,7 |
14,5 |
22,5 |
17,0 |
– |
200-315 |
355-630 |
710 |
|
D |
8,1 |
20,0 |
37,0 |
24,0 |
– |
315-450 |
600-900 |
1000 |
|
E |
9,6 |
23,5 |
44,5 |
29,0 |
– |
500-560 |
630-1120 |
1250 |
|
E0 |
12,5 |
31,0 |
58,0 |
38,0 |
– |
– |
800-1400 |
1600 |
Таблица 12.7 Размеры и параметры клиновых ремней


Таблица 12.7
Размеры и параметры клиновых ремней
|
Тип |
Обозначение сечения |
Размеры сечения, мм |
F, мм2 |
L, м |
Dmin, мм |
М1, Нм |
||||
|
b |
bp |
h |
y0 |
|||||||
|
Нормального сечения |
Z |
10 |
8,5 |
6 |
2,1 |
47 |
0,4-2,5 |
63 |
≤30 |
|
|
A |
13 |
11 |
8 |
2,8 |
81 |
0,56-4,0 |
90 |
15-60 |
||
|
B |
17 |
14 |
10,5 |
4 |
138 |
0,8-6,3 |
125 |
50-150 |
||
|
C |
22 |
19 |
13,5 |
4,8 |
230 |
1,8-10 |
200 |
120-600 |
||
|
D |
32 |
27 |
19 |
6,9 |
476 |
3,15-15 |
315 |
450-2400 |
||
|
E |
38 |
32 |
23,5 |
8,3 |
692 |
4,5-18 |
500 |
1600-6000 |
||
|
E0 |
50 |
42 |
30 |
11 |
1170 |
6,3-18 |
800 |
≥4000 |
||
|
Узкие |
УО |
10 |
8,5 |
8 |
2,0 |
56 |
0,63 |
3,55 |
63 |
≤150 |
|
УА |
13 |
11 |
10 |
2,8 |
95 |
0,80 |
4,50 |
90 |
90 |
400 |
|
УБ |
17 |
14 |
13 |
3,5 |
158 |
1,25 |
8,00 |
140 |
300 |
2000 |
Расчет ременной передачи – 3.0 out of
5
based on
41 votes
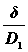 k0, H /мм 2, для
k0, H /мм 2, для