Как найти скорость с дробями

Цели:

• Продолжить формирование умений решать задачи на движение в соединении с темой «Дроби».
• Производить соответствующие записи и вычисления.
• Развивать логическое мышление и внимание.
• Развивать умение анализировать и обобщать.
• Учить изменять условия задачи.

Ход урока

1. Орг. момент

– Что изучаем? (Дробные числа).

– Какого типа задачи учимся решать? (На движение).

– Какие 3 величины там обязательно должны быть (S, V, t).

– Сегодня мы попробуем соединить эти две темы.

– Как и где это возможно сделать? (В задачах на движение).

– Это мы попробуем сделать позже, а сначала немного повторим.

2. Устный счет.

Учитель пишет на доске.

– Найти: 1/2 от 48, 1/2 от 96, 1/2 от 78.

– Какая разница. Находим доли от числа и числа по доле.

– Объясните, как вы находили. На сколько частей делим?

– Как можно по-другому назвать 1/2.

– Найти 1/4 от 60 мин, 1/7 от 84.

– А если взять ⅔, то сколько частей надо взять.

– Сколько раз надо взять по 1/10 круга, чтобы получить целый круг?

– Сколько раз содержится в 1 круге по 1/2 .

– А по 1/4 , а по 1/10, а по 1/8.

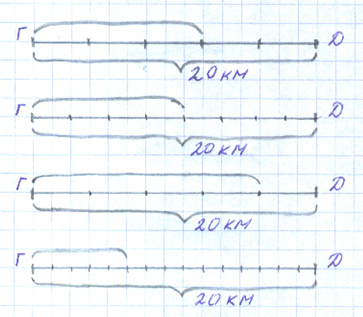
От города до деревни 20км. Асфальтом покрыто 4/5.

Выбери схему, которая соответствует данному решению.

3. Подготовка к решению задач.

– Найдите её и докажите, что это так (у нас дробь 4/5, этот отрезок разделён на 5 частей и мы взяли 4 части).

 – Почему не подходят все остальные схемы и какие дроби на них получились? (Подписываем над отрезками).

– Какое же количество асфальта покрыто в 3 задаче? Как узнать?

20:5 • 4 = 16 км

Сколько же действий нам потребовалось, чтобы найти 4/5 (2).

– Какие? (Деление и умножение).

– Почему? (Делили на части, а потом брали их).

4. Решение задач.

Итак, мы с вами решили, что дробные числа можно применять в задачах на движение. Давайте подумаем и приведем примеры, как это возможно.

Задача. На путь из одного города в другой почтовый голубь затратил 8 часов. Из них ⅟4 он отдыхал, а остальное время летел со скоростью 10км/ч. На каком расстоянии находятся друг от друга города?

– На какую тему эта задача? (На движение).

– Какие три величины всегда есть в таких задачах? (v, t, s).

– Чертим таблицу. Читаем задачу по частям и постепенно заполняем таблицу.

T	V	S
Всего 8 ч. Отдых ? 1/4 часть Остальное – ? ч.	10км/ч	?км

Читаем 1 предложение.

– Что такое 8 часов? (Время).

– Читаем 2 предложение (в какую графу пишем?)

– Какое время он летел? (Остальное).

– (1 ученик по таблице рассказывает еще раз условие).

– Нам нужно узнать расстояние. Какие два данных нужны, чтобы ответить на вопрос (t и v).

– Какую знаем уже? (Cкорость).

– Какова же она? (10 км/ч)

– Какое данное неизвестно? (Время).

– Смотрим на 1 графу и выделяем 1 простую задачу.

1. 8 : 4 × 1 = 2ч он отдыхал.

Рассуждаем дальше:

Сколько времени он потратил непосредственно при перелёте из одного города в другой?

Формулируем вторую простую задачу.

2. 8 – 2 = 6ч он летел (время в пути).

Рассуждаем дальше.

Формулируем 3 простую задачу. (Записываем формулу) S = v × t

3. 10  = 60км расстояние между городами.

Записываем ответ.

– Как изменить условие задачи так, чтобы решение стало короче? Что для этого нужно изменить в таблице (время).

– Как? (Просто записать количество часов).

Записываем.

Сформулируем задачу.

Как узнаем (это последнее действие предыдущей задачи).

– Решаем, пишем формулу.

– Как изменить условие задачи, чтобы решение стало длиннее?

– Что нужно сделать? (оставить условие, усложнив его).

– В какую графу можно добавить новые данные (если дети затрудняются).

– А голубь всегда с одной и той же скоростью летает?

T	V	S
Всего – 8 ч. Отдых 1/4 часть 4 ч Остальные	10км/ч 15км/ч	?км

На путь из одного города в другой почтовый голубь затратил 8 часов. Из них ⅟4 часть он отдыхал. 4 часа летел со скоростью 10км/ч, а остальное время со скоростью 15км/ч. На каком расстоянии находятся друг от друга города?

1. 8 : 4 × 1 = 2ч отдыхал
2. 8 – 2 = 6ч он летел
3. 6 – 4 = 2ч остальное
4. 10 × 4 = 40км за 4 часа
5. 15 × 2 = 30км за 2 часа
6. 40 + 30 = 70км – весь путь
7. Логическая задача.

Выходные дни составляют  недели. Сколько выходных дней в году?

1. 365 : 7 = 52 (ост . 1) недели в году.
2. 7 : 7 × 2 = 2 выходных дня в неделе.
3. 2 × 52 = 104 выходных дня в году.

Сколько же от года отдыхаем в дробях (примерно ).

6. Итог.

Над чем на уроке работали? Что нового узнали? Какие темы соединяли?

Классическим примером текстовой задачи, которая может встретиться вам на ЕГЭ, является задача на движение. Эти задачи довольно разнообразны и включают в себя: задачи на движение навстречу, задачи на движение вдогонку, задачи на движение по реке. И поэтому вопрос, как же решать задачи на движение, иногда ставят учеников в тупик.

Научиться решать такие задачи довольно легко, для этого нужно знать алгоритм, состоящий всего из 3 шагов.

1. Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить
2. Как решать задачи на движение: 3 простых шага
3. Задачи на движение вдогонку: примеры с решением
4. Задачи на движение навстречу: примеры с решением
5. Задачи на движение по течению и против течения: примеры с решением

Формула, которую обязательно нужно знать, и секрет, как ее легко запомнить

Для решения любой задачи на движение вам обязательно нужно знать всего одну формулу, которая вам уже давно известна:И уметь правильно выражать из этой формулы скорость и время:Многие ученики путаются при записи этих формул, допуская ошибки. Чтобы раз и навсегда запомнить формулы нахождения расстояния, скорости и времени, просто нарисуй треугольник. В верхнем углу треугольника напиши S, а внизу — V и t. Проведи горизонтальную черту между ними. Теперь мы можем закрыть рукой ту величину, которую нам нужно найти, и увидим формулу нахождения этой величины. Например, нам нужно найти расстояние. Закрываем рукой S, и на нашем рисунке останется V t – это и есть формула нахождения расстояния. Или нам нужно найти время. Закрываем рукой t, и на нашем рисунке остается  – формула нахождения времени. Нужно найти скорость? Закрываем рукой V, получаем  – формулу нахождения скорости. Главное запомнить, что S должна быть в верхнем углу. Это можно сделать, например, с помощью ассоциации, что S похожа на змею, а змея – хозяйка горы, поэтому она на вершине. Вот как выглядит такой магический треугольник:

Чтобы правильно решить задачу на движение нужно:

1. Определить неизвестное и составить таблицу на основании условия задачи.
2. Составить уравнение на основании таблицы.
3. Вернуться к условиям задачи и записать правильный ответ.

Давайте подробнее разберем каждый шаг:

1. Вначале нам нужно внимательно прочитать условие задачи и определить, что же взять за переменную Х. Чаще всего в задачах на движение удобнее всего за переменную Х обозначить скорость. Если же скорость нам прямо дана в условиях задачи, то за переменную Х обозначаем время. Если в условиях задачи прямо указаны значения и скорости, и времени, тогда за переменную Х берем расстояние. Затем из условий задачи определить все, что нам известно и занести в таблицу.
2. На основании полученной таблицы составляем уравнение и решаем его. После решения уравнения не торопимся записывать ответ. Ведь нахождение Х – это не всегда ответ к исходной задаче. Такую ошибку совершают многие ученики: фактически правильно решив задачу, они записывают неправильный ответ.
3. После решения уравнения возвращаемся к условиям задачи и смотрим, что же требовалось найти. Находим неизвестное и записываем ответ.

Задачи на движение бывают разными. В таких задачах участники движения могут двигаться навстречу друг другу, вдогонку, они могут двигаться по реке (против течения или по течению). Каждая из этих задач имеет особенности решения, о которых мы поговорим ниже и разберем на примерах.

Задачи на движение вдогонку: примеры с решением

При решении задачи, по условия которой оба участника движения двигаются в одном направлении, как правило, сравнивается время их движения. Необходимо запомнить правила:

1. Если время движения сравнивается (то есть присутствуют слова больше/меньше), то мы приравниваем время и прибавляем слагаемое. То есть чтобы получить большее время, мы прибавляем к меньшему времени что-то еще (из условий задачи).
2. Если условия задачи содержат общее время, то дроби, выражающее время, складываются.

Давайте разберем, как работают эти правила при решении задач.

Задача 1

Велосипедист и автомобилист одновременно выехали из пункта А в пункт Б, расстояние между которыми равно 50 км. Известно, что скорость автомобилиста на 40 км/ч больше, чем у велосипедиста, в результате чего автомобилист приехал в пункт Б на 4 часа раньше. Найдите скорость велосипедиста.

Решение:

1. Необходимо определить, что взять за переменную Х и составить таблицу. Вспоминаем, что удобнее всего за Х обозначить скорость в том случае, если она прямо не указано в условиях задачи.

В нашем случае скорость в условиях задачи не указана, поэтому скорость велосипедиста обозначаем за Х.

Составляем таблицу, данные для которой берем из условий задачи.

Итак, расстояние (S) нам известно – 50 км, скорость велосипедиста – х, скорость автомобилиста на 40 км/ч больше, значит она равна х + 40. Чтобы определить время вспоминаем формулу t = S / V и подставляем в нее наши значения. Время, затраченное велосипедистом, получится 50 / х, а время, затраченное автомобилистом — 50 / (х + 40).2. На основании таблицы и условий задачи необходимо составить уравнение.

Из условий задачи нам известно, что автомобилист приехал раньше велосипедиста на 4 часа (смотрим наше первое правило). Это значит, что велосипедист затратил на 4 часа больше времени, чем автомобилист. Следовательно,

50 / (х + 40) + 4 = 50 / х

Решаем полученное уравнение, для этого приводим наши дроби к одному знаменателю:

50х + 4х (х + 40) – 50 (х+40) / х (х + 40) = 0

(50х + 4х² + 160х – 50х – 2000) / х (х+40) = 0

(4х² + 160х – 2000) / (х² + 40х) = 0

Умножим обе части уравнение на х² + 40х:

4х² + 160х – 2000 = 0

Разделим обе части уравнения на 4:

х² + 40х – 500 = 0

Находим дискриминант:

D = 40² – 4 * 1 * (-500) = 3600

Далее находим корни уравнения:

х₁ = 10

х₂ = — 50

3. Возвращаемся к условиям задачи и вспоминаем, что же требовалось найти.

Нам нужно было определить скорость велосипедиста, которую мы обозначили за Х.

Скорость велосипедиста должна быть положительна, поэтому х₂ не подходит по смыслу задачи. Следовательно, нас интересует только х₁ и скорость велосипедиста равна 10 км/ч.

Ответ: 10 км/ч.

Задача 2

Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 80 км. На следующий день он поехал обратно, при этом его скорость была на 2 км/ч больше прежней. По пути велосипедист останавливался и отдыхал 2 часа. В итоге на возвращение из города Б в город А у него ушло времени столько же, сколько на путь из города А в город Б. Найдите скорость велосипедиста на пути из города А в город Б.

Решение:

1. Обозначим скорость велосипедиста на пути из города А в город Б как переменную Х.

Составим таблицу.

Из условий задачи: расстояние — 80 км, скорость велосипедиста во второй день – х. Его скорость во второй день была на 2 км/ч больше, чем в первый день, т.е. в первый день она была ниже, следовательно, скорость велосипедиста в первый день равна х – 2. Определим затраченное велосипедистом время на путь по формуле t = S / V. Тогда время, затраченное в первый день на путь равно 80 / х, во второй день — 80 / (х + 2).2. На основании таблицы и условий задачи составим уравнение.

Из условий задачи нам известно, что во второй день велосипедист останавливался и отдыхал 2 часа, следовательно, в пути он провел на 2 часа меньше (смотрим наше первое правило).  Также нам известно, что общее затраченное велосипедистом время в первый и во второй дни равно. Следовательно:

80 / (х + 2) + 2 =  (80 / х)

Решаем полученное уравнение, для чего приводим дроби к общему знаменателю:

(80х + 160 – 80х – 2х (х+2)) / х (х + 2) = 0

Умножаем обе части уравнения на х (х + 2):

160 – 2х² + 4х = 0

— 2х² — 4х + 160 = 0

Делим обе части уравнения на -2:

х² + 2х – 80 = 0

Находим дискриминант:

D = 2² – 4 * 1 * (-80) = 4 + 320 = 324

Тогда корни уравнения равны:

х₁ = 8

х₂ = — 10

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость велосипедиста на пути из города А в город Б, которую мы обозначали за Х.

Скорость должна быть положительна, поэтому х₂ = — 10 не подходит по смыслу задачи. Следовательно, скорость велосипедиста равна 8.

Ответ: 8 км/ч.

Задачи на движение навстречу: примеры с решением

Главное, что нужно помнить о движении навстречу: скорости участников движения складываются.

В тех случаях, когда нам неизвестно общее расстояние, то есть мы не можем его определить из условий задачи и из составленных уравнений, данное расстояние следует принимать за единицу.

Примеры решения задач на движение навстречу:

Задача 1

Из города А в город Б выехал автомобилист, через 3 часа навстречу ему выехал мотоциклист со скоростью 60 км/ч. Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Расстояние между городами А и Б равно 470 км. Найдите скорость автомобилиста.

Решение:

1. Обозначим скорость автомобилиста как Х.

Автомобилист и мотоциклист встретились на расстоянии 350 км от города А. Следовательно, автомобилист проехал 350 км, а мотоциклист 470 – 350 = 120 км.

Составим таблицу:2. Составим уравнении на основании таблицы и условий задачи.

Из условий задачи известно, что автомобилист ехал на 3 часа дольше, чем мотоциклист (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Следовательно:

350/х = 120/60 + 3

350/х = 5

Решаем полученное уравнение:

5х = 350

х = 70

3. Возвращаемся к условиям задачи. Нам необходимо было найти скорость автомобилиста, которую мы обозначали за Х. Следовательно, скорость автомобилиста равна 70 км/ч.

Ответ: 70 км/ч.

Задача 2

Из городов А и Б одновременно навстречу друг другу выехали автомобилист и велосипедист. Автомобилист приехал в город А на 6 часов раньше, чем велосипедист приехал в город Б. Встретились они через 4 часа после начала движения. Сколько времени затратил автомобилист на путь из города Б в город А?

Решение:

1. Время автомобилиста обозначим как Х.

Примем расстояние между городами А и Б за единицу. Остальные данные берем из условий задачи.

Составим таблицу:2. Составим уравнение на основании таблицы и условий задачи.

Известно, что велосипедист и автомобилист встретились через  4 часа после начала движения  и в сумме преодолели все расстояние от города А до города Б. То есть все расстояние от города А до города Б было преодолено за 4 часа.

Вспоминаем, что при движении навстречу скорости движения участников складываются. Подставим в формулу пути известные нам данные:

((1 / х) +  (1 / (х — 6))) * 4 = 1

Решаем полученное уравнение:

(4 / х) +  (4 / (х — 6)) = 1

Приводим дроби к одному знаменателю:

(4х — 24 + 4х — х² + 6х) / (х (х — 6))  = 0

Делим обе части уравнения на х (х — 6), при условии, что х > 6:

-х² + 14х — 24 = 0

Умножим обе части уравнение на -1:

х² — 14х + 24 = 0

Находим дискриминант нашего квадратного уравнения:

D = 14² – 4 * 1 * 24 = 100

Находим корни уравнения:

х₁ = 12

х₂ = 2

х₂ < 6, следовательно, корнем уравнения не является.

3. Возвращаемся к условиям задачи. Нам необходимо было определить, сколько времени затратил автомобилист на путь из города Б в город А. Это время мы обозначали за Х. Следовательно, автомобилист затратил на путь из города Б в город А 12 часов.

Ответ: 12 часов.

Задачи на движение по течению и против течения: примеры с решением

В условиях задач на движение по реке всегда дано две скорости: собственная скорость судна (скорость, с которой он может двигаться в неподвижной воде) и скорость течения.

При этом возможны две ситуации: когда судно движется по течению и когда судно движется против течения.

Когда судно движется по течению, то течение помогает судну двигаться, оно начинает двигаться быстрее, следовательно, собственная скорость судна и скорость течения складываются.

Когда же судно двигается против течения, то оно ощущает сопротивление, плыть ему становится тяжелее. В этом случае скорость течения будет вычитаться из собственной скорости судна.

Давайте рассмотрим примеры решения задач на движение по реке.

Задача 1

Катер прошел против течения реки 160 км/ч и вернулся в пункт отправления, затратив времени на обратный путь на 8 часов меньше. Найдите скорость катера в неподвижной воде, если известно, что скорость течения реки равна 5 км/ч.

Решение:

1. Обозначим собственную скорость катера – х.

Составим таблицу:2. На основании таблицы и условий задачи составим уравнение.

По условиям задачи известно, что время, затраченное на путь по течению реки, на 8 часов меньше, чем время, затраченное на путь против течения реки (пользуемся первым правилом, которое разбирали при решении задач на движение вдогонку). Соответственно:

160 / (х + 5) + 8 = 160 / (х — 5)

Решаем данное уравнение. Для этого приводим дроби к общему знаменателю:

(160 (х – 5) + 8 (х – 5) (х + 5) – 160 (х + 5)) / (х – 5) (х + 5) = 0

(160х – 800 + (8х – 40) (х + 5) – 160х — 800) / (х – 5) (х + 5)  = 0

Умножаем обе части уравнения на (х – 5) (х + 5):

-1600 + 8х² + 40х – 40х – 200 = 0

8х² – 1800 = 0

8х² = 1800

х² = 225

х_1,2 = ±15

3. Возвращаемся к условию задачи. Нам необходимо было найти собственную скорость катера, которую мы обозначили за Х. Так как скорость не может быть отрицательной, то х₁ = -15 противоречит условию задачи. Следовательно, собственная скорость катера равна 15 км/ч.

Ответ: 15 км/ч.

Задача 2

Моторная лодка вышла в 9:00 из пункта А в пункт Б, расстояние между которыми 30 км. Пробыв в пункте Б 3 часа, моторная лодка повернула назад и вернулась в пункт А в 20:00. Найдите скорость течения реки, если известно, что собственная скорость моторной лодки 8 км/ч.

Решение:

1. Обозначим скорость течения реки за х. Остальные данные берем из условия задачи.

Составим таблицу:2. Составим уравнение.

Нам известно, что моторная лодка начала свое движение в 9:00, а закончила в 20:00, а также в течение этого времени пробыла без движения во время стоянки – 3 часа. Таким образом, общее время движения будет 20 – 9 – 3 = 8 часов. Когда речь идет об общем времени движения, то нам нужно сложить время движения по течению и время движения против течения (пользуемся вторым правилом, которое разбирали при решении задач на движение вдогонку). Получаем:

30 / (8+х) + 30 / (8-х) = 8

Решаем полученное уравнение. Для этого приводим дроби к общему знаменателю:

(30 (8+х) + 30 (8-х) – 8 (8-х) (8+х)) / (8-х) (8+х) = 0

Умножаем обе части уравнения на (8-х) (8+х):

240 + 30х + 240 – 30х – (64 – 8х) (8+х) = 0

480 – 512 – 64х + 64х – 8х² = 0

8х² = 32

х² = 4

х_1,2 = ±2

3. Возвращаемся к условию задачи. Нам необходимо было найти скорость течения, которую мы обозначили за х. Так как скорость не может быть отрицательной, то х₁ = -2 противоречит условию задачи. Следовательно, скорость течения равна 2 км/ч.

Ответ: 2 км/ч.

Итак, мы разобрались, как решать задачи на движения. В ЕГЭ 2023 помимо задач на движение могут содержаться и другие текстовые задачи: на смеси и сплавы, на работу, на проценты. О том, как их решать, вы можете узнать на нашем сайте, а также .

ВОРОШИЛОВСКОЕ
ТЕРРИТОРИАЛЬНОЕ УПРАВЛЕНИЕ КОМИТЕТА ПО ОБРАЗОВАНИЮ АДМИНИСТРАЦИИ ВОЛГОГРАДА  

Муниципальное образовательное учреждение
средняя общеобразовательная школа №77

с углубленным изучением отдельных предметов

Ворошиловского района г. Волгограда

Методическая
разработка урока математики в 5 классе

По
теме: Применение обыкновенных дробей при решении задач на движение.

Выполнила:

Сычева В.Н.

Учитель математики

МОУ СОШ №77

ВОЛГОГРАД 2011

Урок
математики в 5 классе

Тема урока: Применение обыкновенных
дробей при решении задач на движение.

Вид урока: урок – путешествие

Тип урока: урок обобщения и
систематизации знаний, умений и навыков.

Цели урока:

1.                
Обобщить
и систематизировать знания о решении задач на движение.

2.                
Расширить
знания обучающихся о космосе

Задачи урока:                                 

·                    
Развитие умения
анализировать и решать задачи по схемам

·                    
Формирование
положительной мотивации и интереса к предмету

Оборудование и материалы
урока:

·                    
Мультимедийный
проектор

·                    
Экран

·                    
Слайдовая
презентация

·                    
Раздаточный
материал

Ход урока

Учитель: В
течение нескольких предыдущих уроков вы изучали тему «Обыкновенные дроби»,
учились их складывать и вычитать.  Сегодня на уроке мы должны увидеть, где мы
можем применить полученные знания и умения, но урок сегодня у нас пройдет
необычно.

Ребята вы знаете
в честь какого события назван 2011 год? (В честь пятидесятилетия первого
полета в космос) А кто совершил этот полет? (Юрий Алексеевич Гагарин)
Мы с вами тоже сегодня отправимся в путешествие по космосу. Опустите головы,
закройте глаза и повторяйте за мной:

Раз,
два! Скорость света.

Три,
четыре! Мы летим.

На
далекие планеты,

Поскорей
попасть хотим!

Так как мы
сегодня с вами путешествуем, а путешествие это всегда движение, то основной
нашей деятельностью на уроке будет – решение задач на движение. И мы с вами как
раз посмотрим как можно использовать правила сложения и вычитания обыкновенных
дробей при решении задач.

Но сначала проверим вашу готовность к
полету (Слайд №3, на экране появляются примеры, которые нужно выполнить
устно).

Подготовка к полету 5-7 мин.

Вычислить устно:

Раз мы собираемся
решать задачи на движение давайте вспомним, какие компоненты в них
присутствуют? (скорость, время, расстояние)

Как найти:

Расстояние = скорость
* время, скорость = расстояние/время,

Время = расстояние/скорость

Компоненты
вспомнили, связь между ними установили, к полету готовы?! (Готовы)

Много
планет вокруг солнца летает.

Может
быть люди на них обитают?

Давайте
в ракету мы сядем скорей,

Чтоб
на луне оказаться быстрей

(Слайд №4) У нашего космического
корабля очень маленький топливный бак. Для того чтобы мы могли совершить свой
полет, нам потребуется совершить несколько остановок на станциях для
дозаправки. Название каждой станции соответствует заданию, которое нужно
выполнить. Полетели на первую станцию?! Но для того, чтобы нас заправили нам
нужно пройти испытание. (Слайд №5 задание появляется на экране и выполняется
устно).

1. Какое
именованное число лишнее в каждом столбике: (3 мин)

6 м/сек 280 км/ч 18 м/мин 108 мин 65 м/ч

83518 дм2 92300 см2 65540 км2 10800 мм2 384400 км

18 мин 220 км/с 30 сек 65 час 5 суток

Выбрав лишнее
число в первом столбике вы узнаете: Сколько минут Юрий Гагарин пробыл в космосе
(108 мин); во втором столбике: Какое расстояние от Земли до Луны (384400 км); в
третьем столбике: Какова скорость вращения солнца вокруг галактического центра
(220 км/ч). Запас знаний о космосе пополнили.

Давайте откроем
тетради и запишем сегодняшнее число и тему нашего урока.

Полетели на
следующую станцию.

2. Переведите
в другую единицу измерения? (Слайд №6 задание появляется на экране. Один ученик
вызывается к доске для решения, все остальные записывают решение в тетрадях). 7
мин.

1 час 28 мин = 88 мин столько земных
суток длится год на Меркурии;

3 часа 45 мин = 225 мин столько
земных суток длится год на Венере;

1 м 6 дм 5 см = 165 см столько земных
суток длится год на Нептуне;

2 дм 2 см 6 мм = 226 мм за столько
миллионов лет Солнце делает полный оборот вокруг центра нашей вселенной.

И так и это
испытание пройдено. Наконец-то мы добрались до Луны. Для того чтобы
передвигаться по Луне нам предложили следующие средства передвижения: ковер –
самокат и сапоги скороходы. И предлагают решить задачу.

3. Решить
задачу. (Слайд №7 краткое условие переписывается с экрана, ведется беседа по
этой задаче, затем решение выносится на доску) 7-10 мин

Ковёр – самолёт
пролетает 480 км за 2 часа, а скорость сапогов скороходов в 2 раза меньше
скорости ковра – самолёта. За какое время это расстояние пролетят скороходы?
(ответ дайте в минутах)

Можем ли мы сразу
найти время скороходов?(Нет)

Что нам
неизвестно? (Скорость)

Можем мы сразу ее
узнать? (Нет)

Что мы должны
сначала найти? (Скорость ковра)

Мы можем ее
найти? (Да)

Как? (Один
человек вызывается к доске)

Полетели на
следующую станцию

4. Как найти
скорость сближения и скорость удаления?

Возможна ли
встреча на схемах? (Слайд №9)

                               

1)            
_________________  
скорость сближения равна сумме скоростей

                              

2)          _______________                  скорость
сближения равна разности

                                           
       скоростей

                               

3)      __________________        скорость удаления
равна разности

                                           скоростей

4)         ___________________    скорость удаления
равна сумме скоростей

5. Решить
задачу (Слайд №10 краткое условие на экране, решение записывается на доске и в
тетрадях, )

Два космических
вездехода выехали одновременно навстречу друг другу. Скорость одного вездехода  км/ч, а
другого  км/ч.
Какое расстояние будет между ними через 1 час? Через 3 часа?

Решение задачи
записывается в тетрадях.

6. Самопроверка

1 вариант I. II. III.

2 вариант I. II. III.

Итоги. (Слайд №4) Давайте вспомним,
что мы сегодня делали на уроке? Ребята вам понравился наш сегодняшний урок? Вы
узнали для себя что-нибудь новое?

Домашнее
задание.
Составить и решить задачу по стихотворению.

Вот пешеход бредёт едва

До пункта «Б» из пункта «А»…
Сорок восемь километров!

Против бурь и против ветров!
Ноги его заплетаются,

И с пути он всё время сбивается,

И тяжко бедняге приходится,
И с ответом никак он не сходится!
И в холод, и в тьму навстречу ему.
Выходит другой пешеход.
Он тоже идёт, идёт… И час он идёт, и два,
И болит у него голова…
И не виден никто впереди…

И, наверно, он сбился с пути!..
А дорога все не кончается,

А задача не получается!..

Мне было очень
приятно с вами работать. Всем спасибо за урок.

Задачи на движение — один из самых распространенных видов задач алгебры. Простейшие задачи на движение изучаются еще в начальной школе. В 6-7 классах решение задач на движение сводится к линейному уравнению либо системе линейных уравнений. Здесь мы рассмотрим задачи на движение, которые можно решить с помощью дробного рационального уравнения. При решении задач на движение используем формулу пути:

   

где s — путь, v — скорость, t — время. Как правило, в задачах на движение в 8 классе нужно выразить время через путь и скорость:

   

Чаще всего путь измеряется в километрах, скорость — в километрах в час, время — в часах. Время, заданное в минутах, нужно перевести в часы. Так как в 1 часе 60 минут, то 1 минута — это одна шестидесятая часа, а t минут — t шестидесятых часа:

1 (мин)=1/60(часа). t (мин)=t/60 (часа).

1) Из пункта А в пункт В автомобиль ехал по шоссе протяженностью 210 километров, а возвращался назад по грунтовой дороге протяженность. 160 километров, затратив на обратный путь на 1 час больше, чем на путь из А в В. Найти, с какой скоростью автомобиль двигался по грунтовой дороге, если она на 30 километров в час меньше его скорости по шоссе.

Решение:

Пусть х км/ч — скорость автомобиля по грунтовой дороге, тогда его скорость по шоссе равна (х+30) км/ч.

Составим и решим уравнение:

   

   

   

   

   

   

   

Второй корень не подходит по смыслу задачи, так как скорость не может быть отрицательным числом. Значит, автомобиль по грунтовой дороге двигался со скоростью 40 км/ч.

Ответ: 40 км/ч.

2) Первые 20 км пути велосипедист двигался со скоростью, на 5 км/ч большей скорости, с которой он ехал последние 20 км. С какой скоростью велосипедист проехал вторую половину пути, если на весь путь он затратил 3 часа 20 минут?

Решение:

Пусть II половину пути велосипедист двигался со скоростью х км/ч, тогда его скорость на I половине пути была (х+5)км/ч.

3 часа 20 минут = 3 20/60 =3 1/3 = 10/3 часа.

Составим и решим уравнение:

   

Упростим уравнение, разделив почленно обе его части на 10:

   

   

   

   

   

   

   

Второй корень не подходит по смыслу задачи, так как скорость не может быть отрицательным числом. Значит, II половину пути велосипедист проехал со скоростью 10 км/ч.

Ответ: 10 км/ч.